-
1950年黄昆先生与A. Rhys(里斯, 黄昆先生夫人, 中文名李爱扶)发表了F-中心的光吸收与非辐射跃迁理论的论文, 这一论文被公认为是处理电子-声子互作用在固体缺陷光吸收的先驱开创性量子理论工作, 其中首先由黄昆先生所推导和明确的一个用于表征电子-声子耦合强度的无量纲因子, 被广泛采用和推崇为黄-里斯因子(Huang-Rhys factor), 也被简称为S因子. 本文试图总结黄-里斯因子的物理内涵, 以及它在阐释几种固体有关光学性质中的关键作用, 包括在深缺陷中心发光以及带边浅杂质束缚激子发光中的支配作用. 研究发现, 在不同性质的固体材料中, 电子(激子)-声子耦合强度可以分为极弱耦合(黄-里斯因子远远小于1)、中等耦合(黄-里斯因子在1—5之间)以及强耦合(黄-里斯因子远远大于1)等几种情况. 限于篇幅及个人理解, 本文仅讨论GaN各种带边激子、二维单原子层半导体激子、无机卤族钙钛矿纳米晶片激子以及金刚石单晶中NV复合中心等极弱及中等强度耦合等几种情况, 以纪念黄昆先生诞辰百周年.Huang and Rhys published a quantum theoretical treatment to the light absorption in F-centre in solids, which has been widely recognized as the first detailed quantum-mechanical calculation. In the Huang-Rhys’s seminal theoretical treatment, they derived a dimensionless factor to characterize electron-phonon coupling strength which was named later as Huang-Rhys factor. Since then, Huang-Rhys factor has been generally accepted. In this short review, the physical nature of Huang-Rhys factor and several application examples in solids are introduced and presented in memory of the hundredth anniversary of Prof. Kun Huang. Due to limited publication space and my personal understanding on Huang-Rhys factor, only several cases including GaN, 2D WS2 monolayer semiconductor, inorganic CsPbBr3 perovskite nanosheets and NV centers in diamond, in which the extremely-weak and medium strong coupling between electron (exciton) and phonon occur, are discussed in this short review.
-
Keywords:
- phonon-electron interactions /
- Huang-Rhys factor /
- optical properties of solids /
- luminescence
[1] Huang K, Rhys A 1950 Proc. Roy. Soc. London A 204 406
Google Scholar
[2] Lax M 1952 J. Chem. Phys. 20 1752
Google Scholar
[3] O’Rourke RC 1953 Phys. Rev. 91 265
Google Scholar
[4] Kubo R, Toyozawa Y 1955 Prog. Theoret. Phys. 13 160
Google Scholar
[5] Hopfield J J 1959 J. Phys. Chem. Solids 10 110
Google Scholar
[6] Pryce M H L 1966 Phonons in Perfect Lattices and in Lattices with Point Imperfections (Edinburgh: Oliver & Boyd)
[7] Stoneham A M 1975 Theory of Defects in Solids (Oxford: Clarendon Press)
[8] 黄昆 1981 物理学进展 1 31
Google Scholar
Huang K 1981 Prog. Phys. 1 31
Google Scholar
[9] Lemos A M, Markham J J 1965 J. Phys. Chem. Solids 26 1837
Google Scholar
[10] MulazziE, Terzi N 1967 J. Phys. Colloques 28 C4
[11] Moreno M, BarriusoM T, Aramburu J A 1992 J. Phys.: Conden. Matter 4 9481
[12] Schenk A 1992 Solid-State Electron. 35 1585
Google Scholar
[13] Neumark G F, KosaiK 1983 in Willardson R K, BeerA C ed. Semiconductors and Semimetals Vol. 19 (New York: Academic Press Inc.) Chap. 1 p38
[14] Segall B, Mahan G D 1968 Phys. Rev. 171 935
Google Scholar
[15] Xu S J, Li G Q, Xiong S J, Tong S Y, Che C M, Liu W, Li M F 2005 J. Chem. Phys. 122 244712
Google Scholar
[16] Xu S J, Li G Q, Xiong S J, Che C M 2006 J. Appl. Phys. 99 073508
Google Scholar
[17] Toyozawa T 1970 J. Lumin. 1−2 732
[18] Duke C B, Mahan G D 1965 Phys. Rev. A 139 A1965
Google Scholar
[19] Ridley B K 1978 J. Phys. C: Solid State Phys. 11 2323
Google Scholar
[20] Kovarskii V A 1962 Sov. Phys.-Solid St. 4 1200
[21] Halperin B, Englman R 1979 J. Lumin. 20 329
Google Scholar
[22] Ungier W, Suffczynski M, Adamowski J 1981 Phys. Rev. B 24 2109
[23] Wang M Z, Xu S J 2016 Semicond. Sci. Technol. 31 095004
Google Scholar
[24] Monemar B 1974 Phys. Rev. B 10 676
Google Scholar
[25] Xu SJ, Liu W, Li M F 2002 Appl. Phys. Lett. 81 2959
Google Scholar
[26] Kovalev D, Averboukh B, Volm D, Meyer B K, Amano H, Akasaki I 1996 Phys. Rev. B 54 2518
Google Scholar
[27] Wang J, Zheng C C, Ning J Q, Zhang L X, Li W, Ni Z H, Chen Y, Wang J N, Xu S J 2015 Sci. Rep. 5 7687
Google Scholar
[28] Zhang F, Xu S J, Ning J Q, Zheng C C, Zhao D G, Yang H, Che C M 2010 J. Appl. Phys. 108 116103
Google Scholar
[29] Wang X H, Xu S J 2013 Appl. Phys. Lett. 102 181909
[30] Xu S J, Zheng L X, Cheung S H, Xie M H, Tong S Y, Yang H 2002 Appl. Phys. Lett. 81 4389
Google Scholar
[31] Ovchinnikov D, Allain A, Huang Y S, Dumcenco D, Kis A 2014 ACS Nano 8 8174
Google Scholar
[32] Zeng H, Liu G B, Dai J, Yan Y, Zhu B, He R, Xie L, Xu S, Chen X, Yao W, Cui X 2013 Sci. Rep. 3 1608
Google Scholar
[33] Gutiérrez H R, Perea-López N, Elías A L, Berkdemir A, Wang B, Lü R, López-Urías F, Crespi V H, Terrones H, Terrones M 2013 Nano Lett. 13 3447
Google Scholar
[34] Wang X H, Ning J Q, Zheng C C, Zhu B R, Xie L, Wu H S, Xu S J 2015 J. Mater. Chem. C 3 2589
[35] Wang X H, Ning J Q, Su Z C, Zheng C C, Zhu B R, Xie L, Wu H S, Xu S J 2016 RSC Adv. 6 27677
Google Scholar
[36] O’Donnell K P, Chen X 1991 Appl. Phys. Lett. 58 2924
Google Scholar
[37] Wang X H, Su Z C, Ning J Q, Wang M Z, Xu S J, Han S, Jia F, Zhu D L, Lu Y M 2016 J. Phy. D: Appl. Phys. 49 465101
Google Scholar
[38] Protesescu L, Yakunin S, Bodnarchuk M I, Krieg F, Caputo R, Hendon C H, Yang R X, Walsh A, Kovalenko M V 2015 Nano Lett. 15 3692
[39] Bekenstein Y, Koscher B A, Eaton S W, Yang P, Alivisatos A P 2015 J. Am. Chem. Soc. 137 16008
Google Scholar
[40] Gong X, Voznyy O, Jain A, Liu W, Sabatini R, Piontkowski Z, Walters G, Bappi G, Nokhrin S, Bushuyev O, Yuan M, Comin R, McCamant D, Kelley S O, Sargent E H 2018 Nat. Mater. 17 550
Google Scholar
[41] Iaru C M, Geuchies J J, Koenraad P M, Vanmaekelbergh D, Silov A Y 2017 ACS Nano 11 11024
Google Scholar
[42] Saran R, Heuer-Jungemann A, Kanaras A G, Curry R J 2017 Adv. Opt. Mater. 5 1700231
Google Scholar
[43] Lao X, Yang Z, Su Z, Wang Z, Ye H, Wang M, Yao X, Xu S 2018 Nanoscale 10 9949
Google Scholar
[44] Lao X, Yang Z, Su Z, Bao Y, Zhang J, Wang X, Cui X, Wang M, Yao X, Xu S 2019 J. Phys. Chem. C 123 5128
Google Scholar
[45] Yang Z, Wang M, Qiu H, Yao X, Lao X, Xu S, Lin Z, Sun L, Shao J 2018 Adv. Funct. Mater. 28 1705908
Google Scholar
[46] Mukamel S 1995 Principles of Nonlinear Optical Spectroscopy (Oxford, U.K.: Oxford University Press) p 226
[47] Shi S L, Li G Q, Xu S J, Zhao Y, Chen G H 2006 J. Phys. Chem. B 110 10475
[48] Xu S J, Li G Q, Wang Y J, Zhao Y, Chen G H, Zhao D G, Zhu J J, Yang H, Yu D P, Wang J N 2006 Appl. Phys. Lett. 88 083123
Google Scholar
[49] Doherty M W, Manson N B, Delaney P, Jelezko F, Wrachtrup J, Hollenberg L C L 2013 Phys. Rep. 528 1
Google Scholar
[50] Su Z, Ren Z, Bao Y, Lao X, Zhang J, Zhang J, Zhu D, Lu Y, Hao Y, Xu S 2019 J. Mater. Chem. C 7 8086
Google Scholar
[51] Ren Z Y, Zhang J F, Zhang J C, Xu S R, Zhang C F, Su K, Li Y, Hao Y 2018 Chin. Phys. Lett. 35 078101
[52] Maradudin A A 1967 Solid State Phys. 19 1
Google Scholar
[53] Davies G 1974 J. Phys. C: Solid State Phys. 7 3797
Google Scholar
-
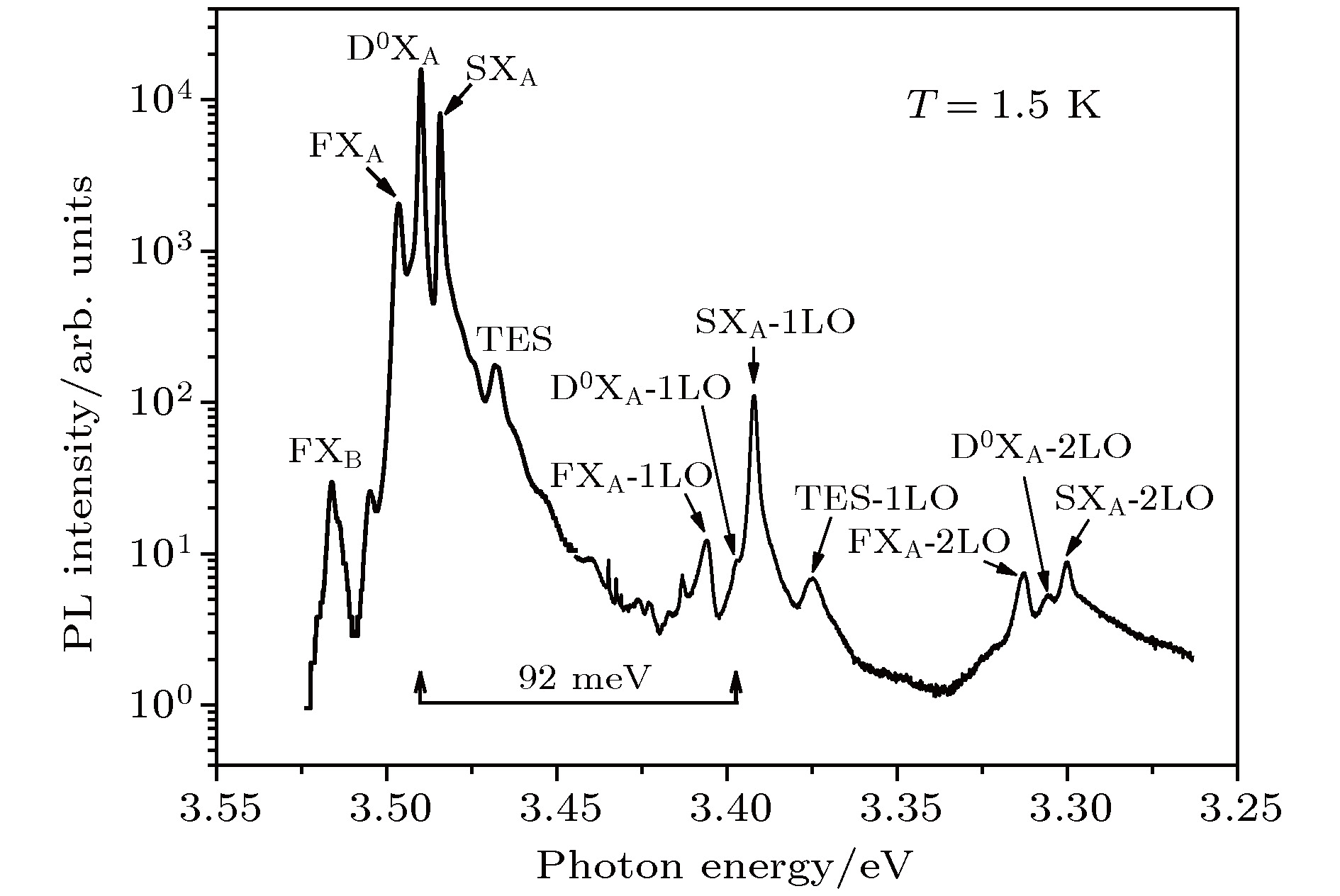
图 1 GaN的1.5 K低温带边PL谱 其中中性施主束缚激子发光峰(D0XA)最强, 其次是A带表面类受主缺陷束缚激子发光峰(SXA)以及A带自由激子发光峰(FXA); 低于这些主要发光峰分别为一个及两个LO声子能量处的发光峰分别为它们的一阶和二阶LO声子侧带; 除这些主要发光峰以及它们的声子侧带外, A带施主束缚激子的双电子跃迁卫星峰(TES)以及B带自由激子发光峰(FXB)仍能分辨
Fig. 1. PL spectrum of the GaN sample at 1.5 K. Three peaks, namely D0XA, SXA, and FXA are the main structures in the PL spectrum. Their first- and second-order LO phonon sidebands are clearly seen and located at lower energy of one and two LO phonon energy, respectively, due to the simultaneous emission of one and two LO phonons. In addition to these distinctive structures, TES and FXB peaks can be also resolved.
图 2 GaN各个激子发光谱线及声子伴线峰值强度实验值, 它们的黄-里斯因子由一阶声子伴线与零声子线的高度比值给出很显然, 在低端低温下, GaN各种激子与LO声子的互作用十分微弱, 即使其中最强的表面缺陷束缚激子的黄-里斯因子也仅有百分之一左右; 这些结果表明, 在极端低温条件下, 伴随GaN各种激子辐射复合的晶格弛豫非常小; 但是如此的结论并不一定适用于中高温情况, 因为激子-声子互作用可能是一个温度的强函数, 尤其是对于自由激子而言
Fig. 2. Experimental peak-intensity values of various excitonic luminescence lines of GaN at 1.5 K. Huang-Rhys factors of various excitons are simply determined by the peak-intensity ratios of the first-order LO phonon sidebands and their respective ZPL lines. Clearly, the coupling strength of various excitons with LO phonons is very weak at 1.5 K. For example, the Huang-Rhys factor of acceptor-like surface-defect bound excitons was only ~1.37 × 10－2, suggesting thatvery small amount of lattice relaxation occurs during the radiative recombination of various excitons of GaN at extremely low temperatures. However, it is worth pointing out that such concluding point may not be valid at medium and high temperatures because the interactions between exciton and phonon could be a strong function of temperature, especially for free excitons.
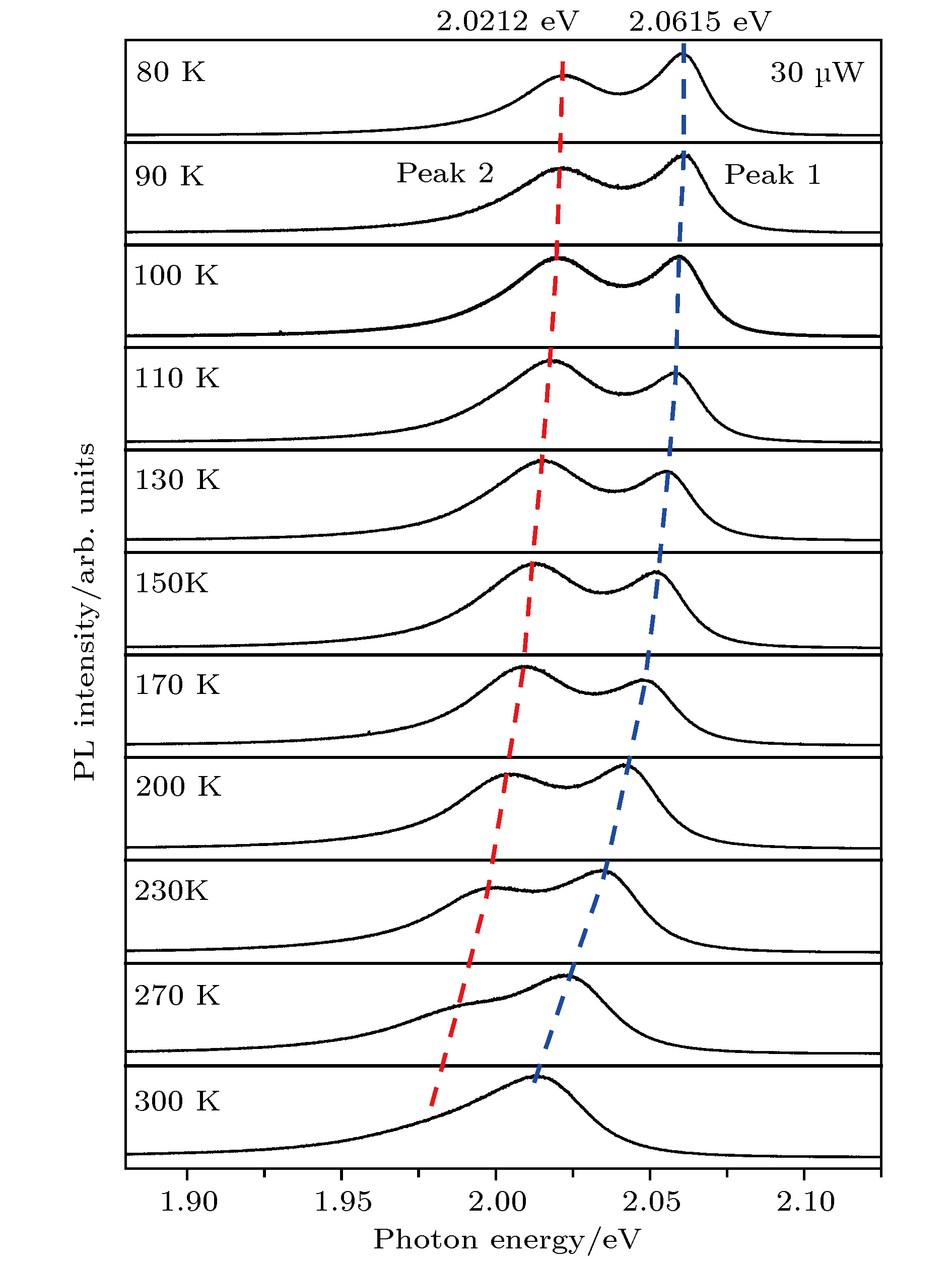
图 3 WS2单原子层二维半导体的变温PL谱 双发光峰及其峰位随温度向低能方向移动(红移)趋势清晰可辨, 而如此的带边发光峰峰位随温度红移的规律有可能是激子-声子耦合造成的
Fig. 3. Variable-temperature PL spectra of the WS2 monolayer semiconductor. Double PL peaks can be well resolved. The red-shift temperature dependence of their peak positions is clearly seen. Note that the red-shift dependence of peak positions of the two emission peaks may be due to the exciton-phonon coupling.
图 4 WS2单原子层二维半导体的两个发光峰位(方块和圆点)随温度的变化趋势, 实线是用O’Donnell与Chen[36]所建议的电子-声子耦合所引起的带隙红移三参数理论公式所得到的拟合曲线
Fig. 4. PL Peak positions (filled squares and circles) of the WS2 monolayer semiconductor vs. temperature. Solid lines are the fitting curves with the bandgap red-shift formula due to electron-phonon coupling suggested by O’Donnell and Chen[36].
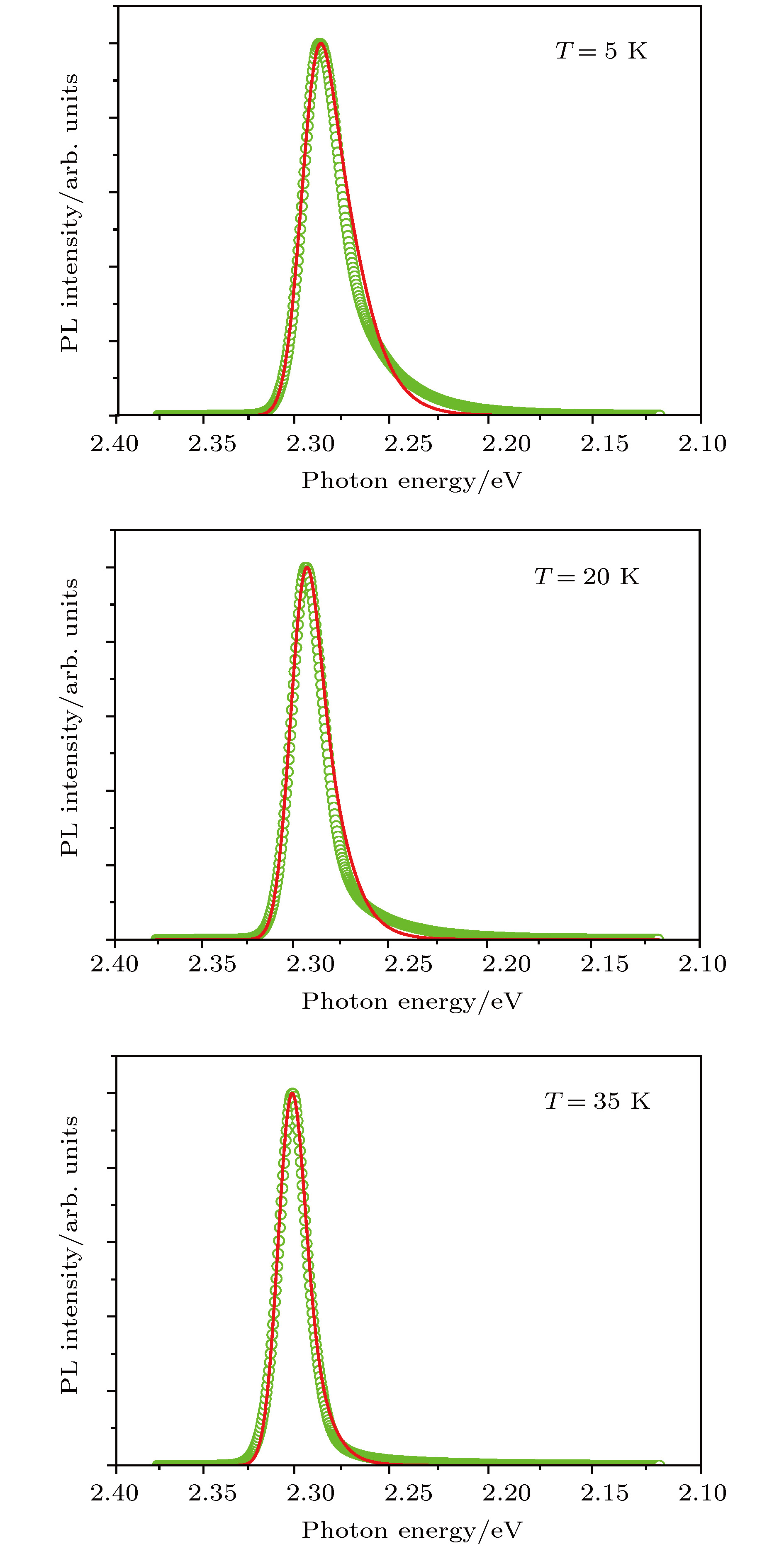
图 5 CsPbBr3纳米晶片在三个不同温度下所测得的PL谱(空圆圈), 实线则为用考虑了电子与多模声子相耦合的多模布朗振子(MBO)模型所计算的理论曲线, 考虑到固体系统中有无穷多的复杂多体互作用, 实验谱线和相对简单的多模布朗振子模型理论谱线符合程度可以说是相当令人满意的
Fig. 5. PL spectra (open circles) of the CsPbBr3 nanosheets measured at three different temperatures. Solid lines are the theoretical curves with the multiple mode Brownian oscillator (MBO) model. Agreement between experiment and theory is satisfactory if considering the complexity of many-body interactions in a solid system.
图 6 用MBO理论模型所拟合出的CsPbBr3纳米晶片在5—40 K低温范围内的黄-里斯因子(实三角), 实线则为线性拟合线 注意, 在5—40 K温度范围内, 黄-里斯因子随温度上升而减小, 表明激子-声子耦合强度是随温度上升而下降的
Fig. 6. Huang-Rhys factors (solid triangles) of the CsPbBr3 nanosheets in the low temperature of 5－40 K with MBO model. Solid line is a linear fitting curve. Note that the Huang-Rhys factor of excitons in the CsPbBr3 nanosheets interestingly decreases with increasing the temperature.
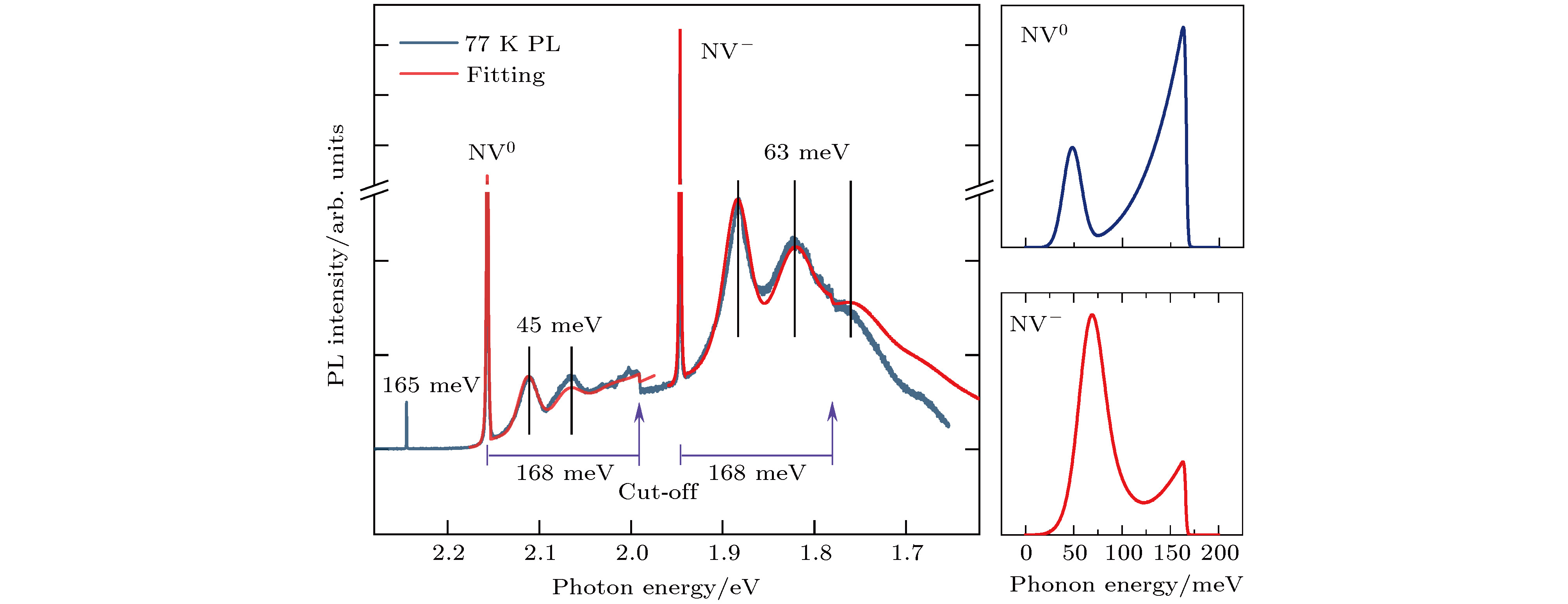
图 7 同质外延生长的金刚石晶片的低温PL谱 NV缺陷中心两种荷电状态的零声子发光谱线以及它们的准局域振动模的周期谱结构清晰可见, 图中若干朝下的箭头标出了这种由于电子与准局域振动模耦合造成的周期性结构; 注意, NV缺陷中心的两种电荷状态所展现出的周期性发光结构具有不同的能量周期, 表明它们各自感受到不同的局域振动模
Fig. 7. 77 K PL spectrum of the diamond flake grown on diamond substrate. It is clearly seen that two sharp lines of NV0 and NV－ as well as their respective phonon sidebands for the two quasi-localized vibrational resonances. Downward arrows indicate such phonon sidebands.
图 8 左侧为金刚石晶片的低温PL谱(灰线)以及理论拟合谱线(红线), 金刚石声子的截止能量为168 meV, 与图中的拉曼峰能量(165 meV)很接近; 右侧为对实验谱线进行理论拟合所获得与NV缺陷中心两种荷电态相耦合的准局域振动模的声子态密度
Fig. 8. Left panel: measured 77 K PL spectrum (gray line) of the diamond flake and theoretical spectrum (red line). The cut off energy of phonons of diamond is also given. Right panel: densities of phone states obtained via theoretical fitting to the experimental PL spectrum.
表 1 用(8)式拟合实验点所用的三参数值
Table 1. Values of the three parameters adopted in the fitting to the temperature dependence of peak positions with Eq. (8).
Peak Eg(0)/eV S $\left\langle {\hbar \omega } \right\rangle / \rm{meV} $ 1 2.0610 ± 0.0004 2.1046 ± 0.0972 38.7739 ± 1.9522 2 2.0225 ± 0.0006 1.3664 ± 0.0691 29.0564 ± 2.4535 
下载: 导出CSV
-
[1] Huang K, Rhys A 1950 Proc. Roy. Soc. London A 204 406
Google Scholar
[2] Lax M 1952 J. Chem. Phys. 20 1752
Google Scholar
[3] O’Rourke RC 1953 Phys. Rev. 91 265
Google Scholar
[4] Kubo R, Toyozawa Y 1955 Prog. Theoret. Phys. 13 160
Google Scholar
[5] Hopfield J J 1959 J. Phys. Chem. Solids 10 110
Google Scholar
[6] Pryce M H L 1966 Phonons in Perfect Lattices and in Lattices with Point Imperfections (Edinburgh: Oliver & Boyd)
[7] Stoneham A M 1975 Theory of Defects in Solids (Oxford: Clarendon Press)
[8] 黄昆 1981 物理学进展 1 31
Google Scholar
Huang K 1981 Prog. Phys. 1 31
Google Scholar
[9] Lemos A M, Markham J J 1965 J. Phys. Chem. Solids 26 1837
Google Scholar
[10] MulazziE, Terzi N 1967 J. Phys. Colloques 28 C4
[11] Moreno M, BarriusoM T, Aramburu J A 1992 J. Phys.: Conden. Matter 4 9481
[12] Schenk A 1992 Solid-State Electron. 35 1585
Google Scholar
[13] Neumark G F, KosaiK 1983 in Willardson R K, BeerA C ed. Semiconductors and Semimetals Vol. 19 (New York: Academic Press Inc.) Chap. 1 p38
[14] Segall B, Mahan G D 1968 Phys. Rev. 171 935
Google Scholar
[15] Xu S J, Li G Q, Xiong S J, Tong S Y, Che C M, Liu W, Li M F 2005 J. Chem. Phys. 122 244712
Google Scholar
[16] Xu S J, Li G Q, Xiong S J, Che C M 2006 J. Appl. Phys. 99 073508
Google Scholar
[17] Toyozawa T 1970 J. Lumin. 1−2 732
[18] Duke C B, Mahan G D 1965 Phys. Rev. A 139 A1965
Google Scholar
[19] Ridley B K 1978 J. Phys. C: Solid State Phys. 11 2323
Google Scholar
[20] Kovarskii V A 1962 Sov. Phys.-Solid St. 4 1200
[21] Halperin B, Englman R 1979 J. Lumin. 20 329
Google Scholar
[22] Ungier W, Suffczynski M, Adamowski J 1981 Phys. Rev. B 24 2109
[23] Wang M Z, Xu S J 2016 Semicond. Sci. Technol. 31 095004
Google Scholar
[24] Monemar B 1974 Phys. Rev. B 10 676
Google Scholar
[25] Xu SJ, Liu W, Li M F 2002 Appl. Phys. Lett. 81 2959
Google Scholar
[26] Kovalev D, Averboukh B, Volm D, Meyer B K, Amano H, Akasaki I 1996 Phys. Rev. B 54 2518
Google Scholar
[27] Wang J, Zheng C C, Ning J Q, Zhang L X, Li W, Ni Z H, Chen Y, Wang J N, Xu S J 2015 Sci. Rep. 5 7687
Google Scholar
[28] Zhang F, Xu S J, Ning J Q, Zheng C C, Zhao D G, Yang H, Che C M 2010 J. Appl. Phys. 108 116103
Google Scholar
[29] Wang X H, Xu S J 2013 Appl. Phys. Lett. 102 181909
[30] Xu S J, Zheng L X, Cheung S H, Xie M H, Tong S Y, Yang H 2002 Appl. Phys. Lett. 81 4389
Google Scholar
[31] Ovchinnikov D, Allain A, Huang Y S, Dumcenco D, Kis A 2014 ACS Nano 8 8174
Google Scholar
[32] Zeng H, Liu G B, Dai J, Yan Y, Zhu B, He R, Xie L, Xu S, Chen X, Yao W, Cui X 2013 Sci. Rep. 3 1608
Google Scholar
[33] Gutiérrez H R, Perea-López N, Elías A L, Berkdemir A, Wang B, Lü R, López-Urías F, Crespi V H, Terrones H, Terrones M 2013 Nano Lett. 13 3447
Google Scholar
[34] Wang X H, Ning J Q, Zheng C C, Zhu B R, Xie L, Wu H S, Xu S J 2015 J. Mater. Chem. C 3 2589
[35] Wang X H, Ning J Q, Su Z C, Zheng C C, Zhu B R, Xie L, Wu H S, Xu S J 2016 RSC Adv. 6 27677
Google Scholar
[36] O’Donnell K P, Chen X 1991 Appl. Phys. Lett. 58 2924
Google Scholar
[37] Wang X H, Su Z C, Ning J Q, Wang M Z, Xu S J, Han S, Jia F, Zhu D L, Lu Y M 2016 J. Phy. D: Appl. Phys. 49 465101
Google Scholar
[38] Protesescu L, Yakunin S, Bodnarchuk M I, Krieg F, Caputo R, Hendon C H, Yang R X, Walsh A, Kovalenko M V 2015 Nano Lett. 15 3692
[39] Bekenstein Y, Koscher B A, Eaton S W, Yang P, Alivisatos A P 2015 J. Am. Chem. Soc. 137 16008
Google Scholar
[40] Gong X, Voznyy O, Jain A, Liu W, Sabatini R, Piontkowski Z, Walters G, Bappi G, Nokhrin S, Bushuyev O, Yuan M, Comin R, McCamant D, Kelley S O, Sargent E H 2018 Nat. Mater. 17 550
Google Scholar
[41] Iaru C M, Geuchies J J, Koenraad P M, Vanmaekelbergh D, Silov A Y 2017 ACS Nano 11 11024
Google Scholar
[42] Saran R, Heuer-Jungemann A, Kanaras A G, Curry R J 2017 Adv. Opt. Mater. 5 1700231
Google Scholar
[43] Lao X, Yang Z, Su Z, Wang Z, Ye H, Wang M, Yao X, Xu S 2018 Nanoscale 10 9949
Google Scholar
[44] Lao X, Yang Z, Su Z, Bao Y, Zhang J, Wang X, Cui X, Wang M, Yao X, Xu S 2019 J. Phys. Chem. C 123 5128
Google Scholar
[45] Yang Z, Wang M, Qiu H, Yao X, Lao X, Xu S, Lin Z, Sun L, Shao J 2018 Adv. Funct. Mater. 28 1705908
Google Scholar
[46] Mukamel S 1995 Principles of Nonlinear Optical Spectroscopy (Oxford, U.K.: Oxford University Press) p 226
[47] Shi S L, Li G Q, Xu S J, Zhao Y, Chen G H 2006 J. Phys. Chem. B 110 10475
[48] Xu S J, Li G Q, Wang Y J, Zhao Y, Chen G H, Zhao D G, Zhu J J, Yang H, Yu D P, Wang J N 2006 Appl. Phys. Lett. 88 083123
Google Scholar
[49] Doherty M W, Manson N B, Delaney P, Jelezko F, Wrachtrup J, Hollenberg L C L 2013 Phys. Rep. 528 1
Google Scholar
[50] Su Z, Ren Z, Bao Y, Lao X, Zhang J, Zhang J, Zhu D, Lu Y, Hao Y, Xu S 2019 J. Mater. Chem. C 7 8086
Google Scholar
[51] Ren Z Y, Zhang J F, Zhang J C, Xu S R, Zhang C F, Su K, Li Y, Hao Y 2018 Chin. Phys. Lett. 35 078101
[52] Maradudin A A 1967 Solid State Phys. 19 1
Google Scholar
[53] Davies G 1974 J. Phys. C: Solid State Phys. 7 3797
Google Scholar
下载:
计量
- 文章访问数: 31228
- PDF下载量: 1956
- 被引次数: 0
