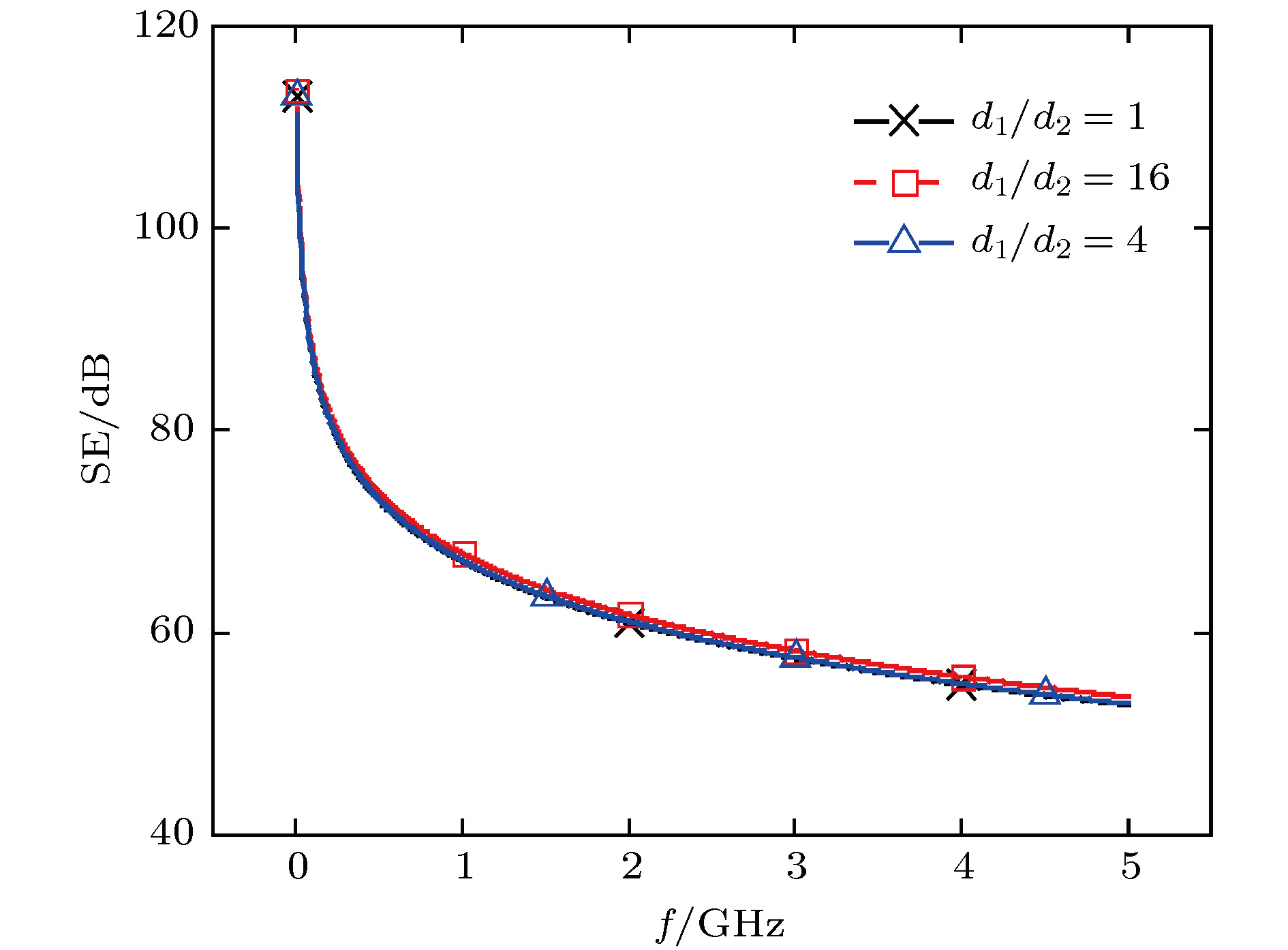
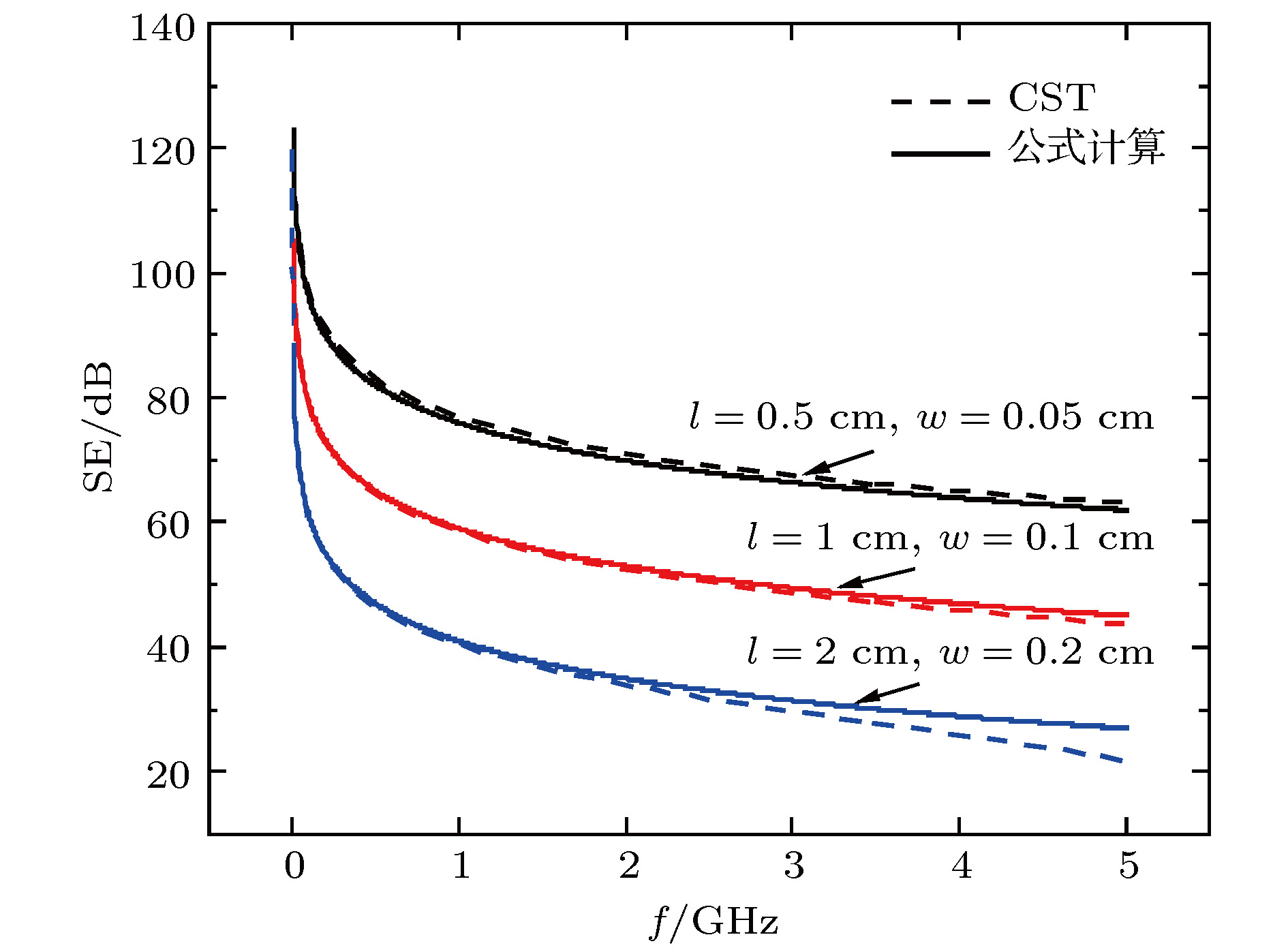
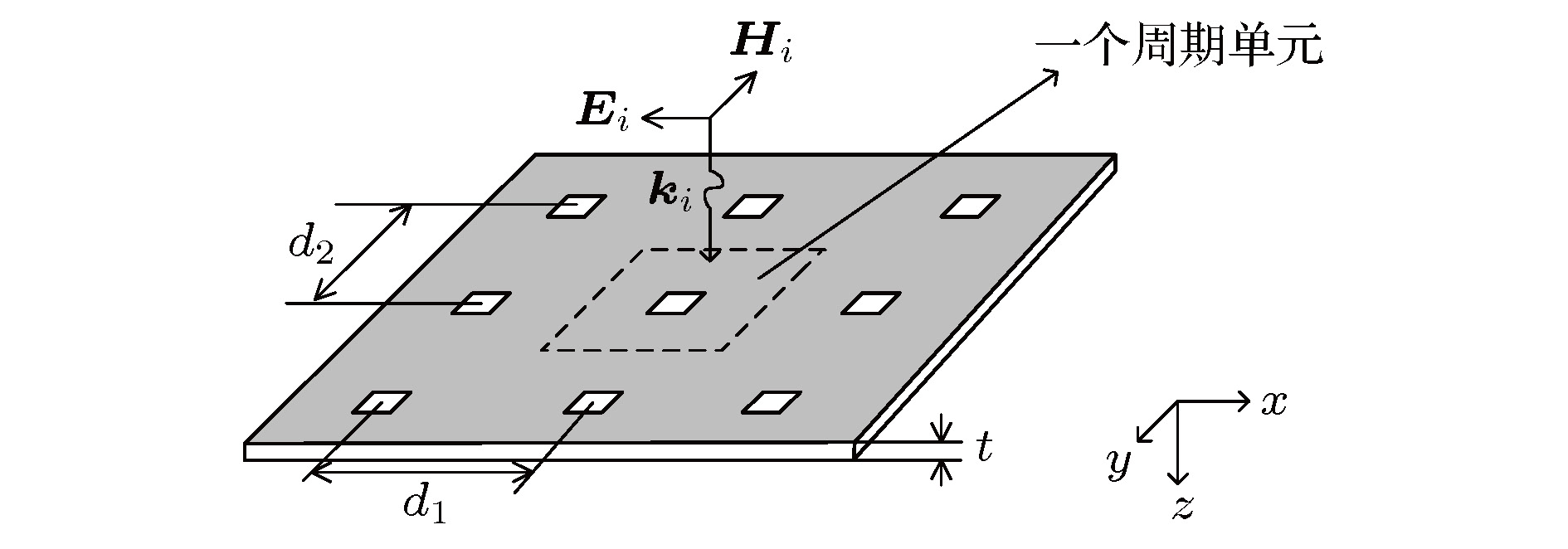
-
本文针对平面电磁波对无限大导体平板上周期孔阵的透射问题, 首先用Bethe小孔理论将孔阵表示成偶极子阵列, 然后用平均化处理得到均匀的等效磁化/极化强度, 进而引入等效面源导出透射电磁波表达式, 最终给出了孔阵对平面电磁波屏蔽效能的解析公式. 该公式分别针对横电和横磁两种极化方式, 将屏蔽效能表示成孔阵周期面积、孔的极化系数、波长和入射角的简单函数, 其计算结果与全波仿真结果一致性好. 结果表明, 透射场强的幅值与孔极化系数和波频率成正比, 与周期面积成反比; 在横电极化方式, 波频率和周期面积不变的情况下, 透射场强的幅值与入射角的余弦值成正比, 入射角越大屏蔽效能越高; 在横磁极化方式下，透射场强幅值与入射角的关系相对复杂, 但在入射角较小时与入射角的余弦值近似成反比, 总体上入射角越大屏蔽效果越低.Penetration of a plane electromagnetic wave through the apertures on a perfectly conducting flat plate is a classical electromagnetic problem. In some practical applications like electromagnetic shielding, where only the fields far from the apertures are concerned and the aperture sizes are small compared with a wavelength, the role of apertures can be represented by the equivalent electric and magnetic dipoles located in the centers of the apertures. In principle, the penetration field can be expressed as the superposition of the radiation fields of the dipoles. However, the direct superposition leads to a double series with complex form and poor convergence. On the other hand, this problem may also be solved by full wave numerical simulations. Even so, finding analytical solutions is still desirable considering that it is clear in physical significance and easy to implement. In this paper, the analytical formula of the penetration fields are derived for both TE and TM polarization mode with different angles of incidence. The derivation is carried out firstly by averagely distributing each dipole moment within each periodic unit. As a result, the dipole array is replaced with a flat sheet with uniform magnetization and polarization intensity. Then, the equivalent surface current and charge distributions are obtained directly from the polarization intensity. Finally, the penetration fields are treated as the radiation fields of the surface sources. It is shown that the amplitude of the penetration field is proportional to aperture magnetic polarization coefficient and wave frequency, and it is inversely proportional to the area of a periodic unit. In regard to the effect of the incidence angle, the amplitude of the penetration field is proportional to the cosine of the incidence angle for TE polarization. However, for the TM polarization, the relationship is a little complicated due to the coexistence of electric and magnetic dipoles: the field is not rigorously inversely proportional to the cosine of the incidence angle due to the existence of a correction term involving both the polarization coefficient and the sine of the angle. The formula is used to calculate the shielding effectiveness for several different aperture shapes and different incidence angles. The results are in good agreement with those from the full wave simulation software.
-
Keywords:
- electromagnetic shielding /
- aperture coupling /
- Bethe’s theory /
- polarizability coefficient
[1] 阚勇, 闫丽萍, 赵翔, 周海京, 刘强, 黄卡玛 2016 65 030702
Google Scholar
Kan Y, Yan L P, Zhao X, Zhou H J, Liu Q, Huang K M 2016 Acta Phys. Sin. 65 030702
Google Scholar
[2] Mcdowell A J, Hubing T H 2014 IEEE Trans. Electromagn. Compat 56 1711
Google Scholar
[3] 焦重庆, 牛帅, 李琳 2015 电工技术学报 30 1
Google Scholar
Jiao C Q, Niu S, Li L 2015 Transactions of China Electrotechnical Society 30 1
Google Scholar
[4] 罗静雯, 杜平安, 任丹, 聂宝林 2015 64 010701
Google Scholar
Luo J W, Du P A, Ren D, Nie B L 2015 Acta Phys. Sin. 64 010701
Google Scholar
[5] 段兴跃, 李小康, 程谋森, 李干 2016 65 197901
Google Scholar
Duan X Y, Li X K, Cheng M S, Li G 2016 Acta Phys. Sin 65 197901
Google Scholar
[6] Nie B L, Du P A, Yu Y T, Shi Z 2011 IEEE Trans. Electromagn. Compat. 53 73
Google Scholar
[7] 任丹, 杜平安, 聂宝林, 曹钟, 刘文奎 2014 63 120701
Google Scholar
Ren D, Du P A, Nie B L, Cao Z, Liu W K 2014 Acta Phys. Sin. 63 120701
Google Scholar
[8] 焦重庆, 牛帅 2013 62 114102
Google Scholar
Jiao C Q, Niu S 2013 Acta Phys. Sin. 62 114102
Google Scholar
[9] Zhao Y L, Ma F H, Li X F, Ma J J, Jia K 2018 Chin. Phys. B 27 027302
Google Scholar
[10] 彭强, 周东方, 侯德亭, 余道杰, 胡涛, 王利萍, 夏蔚 2013 强激光与粒子束 25 2355
Peng Q, Zhou D F, Hou D T, Yu D J, Hu T, Wang L P, Xia W 2013 High Power Laser and Particle Beams 25 2355
[11] Li B, Dong H, Huang X L, Qiu Y, Tao Q, Zhu J M 2018 Chin. Phys. B 27 020701
Google Scholar
[12] 毛湘宇, 杜平安, 聂宝林 2009 系统仿真学报 21 7493
Mao X Y, Du P A, Nie B L 2009 Journal of System Simulation 21 7493
[13] Frikha A, Bensetti M, Duval F, Benjelloun N, Lafon F, Pichon L 2015 IEEE Trans. Magn. 51 1
[14] García-Pérez L G, Lozano-Guerrero A J, Blázquez-Ruiz J M, Valenzuela-Valdés J F, Monzó-Cabrera J, Fayos-Fernández J, Díaz-Morcillo A 2017 IEEE Trans. Electromagn. Compat. 59 789
Google Scholar
[15] Benhassine S, Pichon L, Tabbara W 2002 IEEE Trans. Magn. 38 709
Google Scholar
[16] Ali S, Weile D, Clupper T 2005 IEEE Trans. Electromagn. Compat. 47 367
Google Scholar
[17] Wallyn W, De Zutter D, Rogier H 2002 IEEE Trans. Electromagn. Compat. 44 130
Google Scholar
[18] 焦重庆, 李顺杰 2016 电工技术学报 31 112
Google Scholar
Jiao C Q, Li S J 2016 Transactions of China Electrotechnical Society 31 112
Google Scholar
[19] Robinson M P, Benson T M, Christopoulos C, Dawson J F, Ganley M D, Marvin A C, Porter S J, Thomas D W P 1998 IEEE Trans. Electromagn. Compat. 44 240
[20] 焦重庆, 齐磊 2012 61 134104
Google Scholar
Jiao C Q, Qi L 2012 Acta Phys. Sin. 61 134104
Google Scholar
[21] Otoshi T Y 1972 IEEE Trans. Microwave Theory Tech. 20 235
Google Scholar
[22] Hyun S Y, Jung I, Hong I P, Jung C, Kim E J, Yook J G 2016 IEEE Trans. Electromagn. Compat. 58 911
Google Scholar
[23] Bethe H A 1944 Phys. Rev. 66 163
Google Scholar
[24] Nitsch J B, Tkachenko S V, Potthast S 2012 IEEE Trans. Electromagn. Compat. 54 1252
Google Scholar
[25] Tesche F M, Ianoz M V, Karlsson T 1997 EMC Analysis Methods and Computational Models(New York: John Wiley& Sons)pp208—211
[26] Cohn S B 1951 Proc. IRE 39 1416
Google Scholar
-
图 1 平面波垂直入射开孔导体板示意图
Fig. 1. Conductor plate with holes illuminated by a plane wave with vertical polarization.
图 2 TE极化平面波入射均匀开孔导体板示意图
Fig. 2. Conductor plate with holes illuminated by a plane wave of TE polarization.
图 3 TM极化平面波入射均匀开孔金属板
Fig. 3. Conductor plate with holes illuminated by a plane wave of TM polarization.
图 5 板厚度对屏蔽效能的影响
Fig. 5. Dependence of the SE on frequency for different thicknesses of the plane.
图 6 圆形孔开孔大小对屏蔽效能的影响
Fig. 6. Dependence of the SE on frequency for circular apertures with different radius.
图 8 椭圆孔开孔大小对屏蔽效能的影响
Fig. 8. Dependence of SE on frequency of different elliptical apertures with different size.
图 10 不同形状开孔板的屏蔽效能随频率的变化
Fig. 10. Dependence of SE on frequency of different elliptical apertures with different size.
图 12 混合形状开孔的屏蔽效能随频率的变化
Fig. 12. Dependence of SE on frequency of apertures with mix shape.
图 13 圆形孔屏蔽效能随入射角的变化（r = 0.5 cm）
Fig. 13. Dependence of SE on angle of incidence of different polarization of circular apertures (r = 0.5 cm).
图 14 椭圆孔屏蔽效能随入射角的变化（l = 2 cm）
Fig. 14. Dependence of SE on angle of incidence of different polarization of elliptical apertures (l = 2 cm).
表 1 常见开孔形状极化系数
Table 1. Polarization coefficients of typical opening shapes.
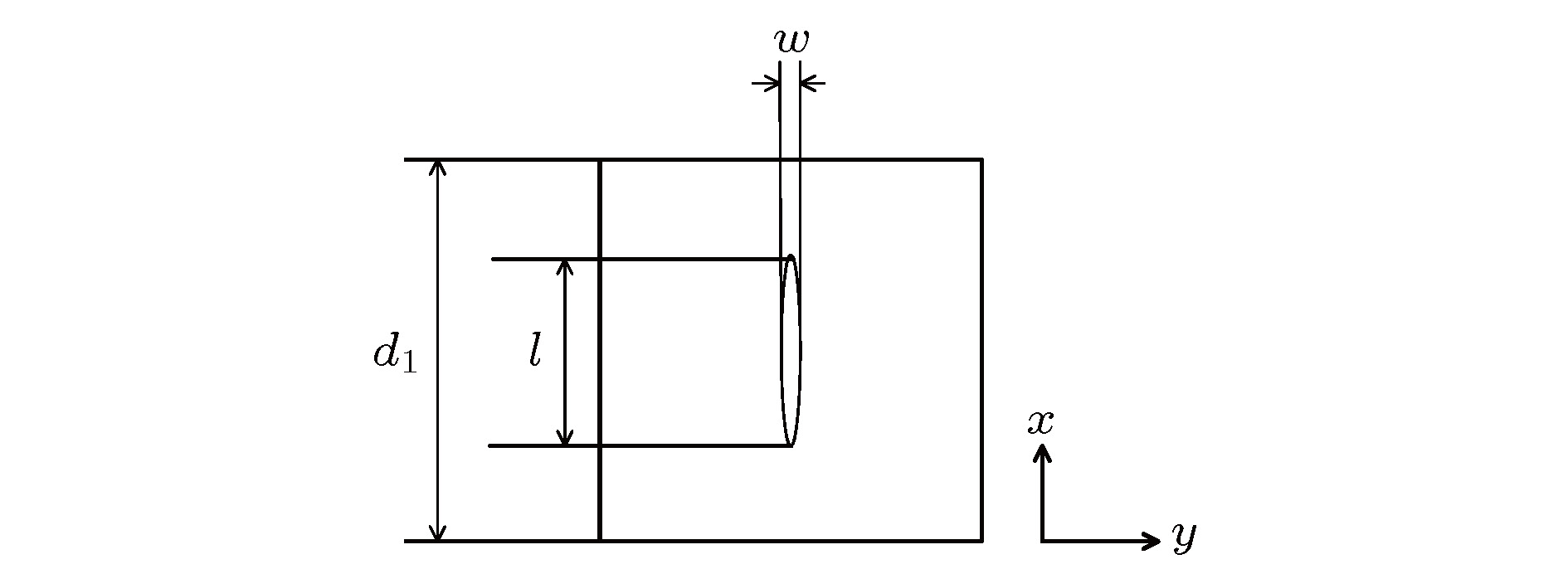
孔形状 ${\alpha _{\rm{e}}}$ ${\alpha _{{\rm{m}}x}}$ ${\alpha _{{\rm{m}}y}}$ 圆形（r为半径） $\frac{{2{r^3}}}{3}$ $\frac{{4{r^3}}}{3}$ $\frac{{4{r^3}}}{3}$ 椭圆（l为长轴，沿x方向，w为短轴） $\frac{{\text{π}}}{{24}} \cdot \frac{{{w^2}l}}{{{\rm{E}}(e)}}$ $\frac{{\text{π}}}{{24}} \cdot \frac{{{e^2}{l^3}}}{{K(e) - E(e)}}$ $\frac{{\text{π}}}{{24}} \cdot \frac{{{e^2}{l^3}}}{{{{(l/w)}^2}E(e) - K(e)}}$ 
下载: 导出CSV
-
[1] 阚勇, 闫丽萍, 赵翔, 周海京, 刘强, 黄卡玛 2016 65 030702
Google Scholar
Kan Y, Yan L P, Zhao X, Zhou H J, Liu Q, Huang K M 2016 Acta Phys. Sin. 65 030702
Google Scholar
[2] Mcdowell A J, Hubing T H 2014 IEEE Trans. Electromagn. Compat 56 1711
Google Scholar
[3] 焦重庆, 牛帅, 李琳 2015 电工技术学报 30 1
Google Scholar
Jiao C Q, Niu S, Li L 2015 Transactions of China Electrotechnical Society 30 1
Google Scholar
[4] 罗静雯, 杜平安, 任丹, 聂宝林 2015 64 010701
Google Scholar
Luo J W, Du P A, Ren D, Nie B L 2015 Acta Phys. Sin. 64 010701
Google Scholar
[5] 段兴跃, 李小康, 程谋森, 李干 2016 65 197901
Google Scholar
Duan X Y, Li X K, Cheng M S, Li G 2016 Acta Phys. Sin 65 197901
Google Scholar
[6] Nie B L, Du P A, Yu Y T, Shi Z 2011 IEEE Trans. Electromagn. Compat. 53 73
Google Scholar
[7] 任丹, 杜平安, 聂宝林, 曹钟, 刘文奎 2014 63 120701
Google Scholar
Ren D, Du P A, Nie B L, Cao Z, Liu W K 2014 Acta Phys. Sin. 63 120701
Google Scholar
[8] 焦重庆, 牛帅 2013 62 114102
Google Scholar
Jiao C Q, Niu S 2013 Acta Phys. Sin. 62 114102
Google Scholar
[9] Zhao Y L, Ma F H, Li X F, Ma J J, Jia K 2018 Chin. Phys. B 27 027302
Google Scholar
[10] 彭强, 周东方, 侯德亭, 余道杰, 胡涛, 王利萍, 夏蔚 2013 强激光与粒子束 25 2355
Peng Q, Zhou D F, Hou D T, Yu D J, Hu T, Wang L P, Xia W 2013 High Power Laser and Particle Beams 25 2355
[11] Li B, Dong H, Huang X L, Qiu Y, Tao Q, Zhu J M 2018 Chin. Phys. B 27 020701
Google Scholar
[12] 毛湘宇, 杜平安, 聂宝林 2009 系统仿真学报 21 7493
Mao X Y, Du P A, Nie B L 2009 Journal of System Simulation 21 7493
[13] Frikha A, Bensetti M, Duval F, Benjelloun N, Lafon F, Pichon L 2015 IEEE Trans. Magn. 51 1
[14] García-Pérez L G, Lozano-Guerrero A J, Blázquez-Ruiz J M, Valenzuela-Valdés J F, Monzó-Cabrera J, Fayos-Fernández J, Díaz-Morcillo A 2017 IEEE Trans. Electromagn. Compat. 59 789
Google Scholar
[15] Benhassine S, Pichon L, Tabbara W 2002 IEEE Trans. Magn. 38 709
Google Scholar
[16] Ali S, Weile D, Clupper T 2005 IEEE Trans. Electromagn. Compat. 47 367
Google Scholar
[17] Wallyn W, De Zutter D, Rogier H 2002 IEEE Trans. Electromagn. Compat. 44 130
Google Scholar
[18] 焦重庆, 李顺杰 2016 电工技术学报 31 112
Google Scholar
Jiao C Q, Li S J 2016 Transactions of China Electrotechnical Society 31 112
Google Scholar
[19] Robinson M P, Benson T M, Christopoulos C, Dawson J F, Ganley M D, Marvin A C, Porter S J, Thomas D W P 1998 IEEE Trans. Electromagn. Compat. 44 240
[20] 焦重庆, 齐磊 2012 61 134104
Google Scholar
Jiao C Q, Qi L 2012 Acta Phys. Sin. 61 134104
Google Scholar
[21] Otoshi T Y 1972 IEEE Trans. Microwave Theory Tech. 20 235
Google Scholar
[22] Hyun S Y, Jung I, Hong I P, Jung C, Kim E J, Yook J G 2016 IEEE Trans. Electromagn. Compat. 58 911
Google Scholar
[23] Bethe H A 1944 Phys. Rev. 66 163
Google Scholar
[24] Nitsch J B, Tkachenko S V, Potthast S 2012 IEEE Trans. Electromagn. Compat. 54 1252
Google Scholar
[25] Tesche F M, Ianoz M V, Karlsson T 1997 EMC Analysis Methods and Computational Models(New York: John Wiley& Sons)pp208—211
[26] Cohn S B 1951 Proc. IRE 39 1416
Google Scholar
下载:
计量
- 文章访问数: 8372
- PDF下载量: 67
- 被引次数: 0
