-
The energy band theory of acoustic crystal provides an important theoretical foundation for controlling the features of sound fields. By utilizing the acoustic flat bands, the sound wave can be effectively modulated to realize the acoustic localization and diffusion. In this work, an artificial gauge field is used to design a system supporting multiple acoustic flat bands, leading to the emergence of diversified acoustic localizations. Initially, cavity resonators, linked with different connectivity based on the field profiles of acoustic resonators, to emulate coupled $ {p_z} $-dipole modes of atomic orbitals. According to the band order of in-phase and out-of-phase modes in two coupled cavities, it can be confirmed that the cross-linked and V-shaped-linked tube structures can achieve the positive coupling and negative coupling, respectively. By introducing positive and negative coupling into a rhombic loop, a synthetic gauge field can be formed due to the $ \pi $ flux phase accumulation of acoustic wave in the loop. Correspondingly, the different geometric phases of acoustic wave in different paths are analogous to the Aharonov-Bohm caging effect. Due to the Aharonov-Bohm caging effect, the introduce of $ \pi $-flux into a rhombic loop causes the dispersion bands to collapse into dispersionless flat bands, providing the opportunity for controlling the localizations of sound fields. According to the finite structures of the cases with and without gauge fluxes, the eigenmodes and energy ratios are analyzed to investigate the sound field distributions. Compared with the zero-flux structure, the acoustic localization can be realized in the bulk and edge of a finite rhombic sonic crystal after introducing an artificial gauge field with a $ \pi $ flux in each plaquette. Here the localized states, induced by Aharonov-Bohm caging effect, are topologically immune to symmetrical structure disorder, indicating that the localized mode relies on the topological feature of the $ \pi $-flux artificial gauge field. Additionally, based on the excitation of flat band eigenstates, the acoustic flat band bound states corresponding to different eigenstates can be obtained. By superimposing acoustic flat band bound states, the amplitude and phase of sound wave can be manipulated at specific locations, realizing the composite flat band bound states with rich acoustic field patterns. Therefore, we achieve different types of acoustic localized states in an acoustic topological Aharonov-Bohm cage. These localized states can be excited in any primitive cell of the rhombic lattices, and possess the remarkable ability to trap sound waves at different bulk gap frequencies, which achieves the broadband sound localizations. At the eigenfrequencies of flat bands, the localized states will be transformed into the extended states, exhibiting acoustic filtering functionality. Therefore, the acoustic Aharonov-Bohm cage is promising for applications at bandgap and flat band frequencies. The findings in this work provide the theoretical guidance for exploring the acoustic localized states with artificial gauge field, and can realize potential applications in acoustic control devices. -
Keywords:
- sonic crystals /
- acoustic localized states /
- acoustic topological edge states /
- artificial gauge field
-
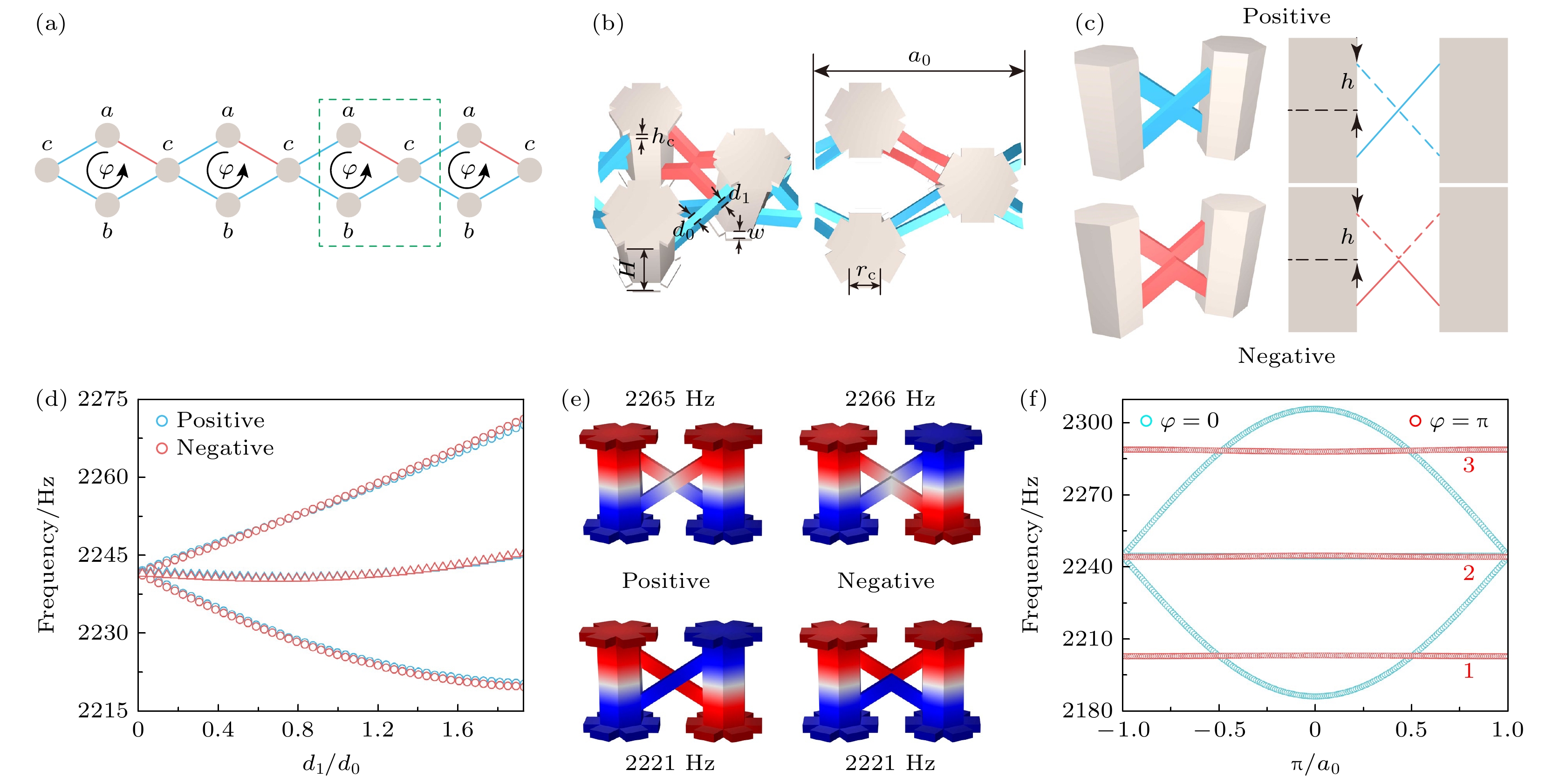
图 1 规范通量为$ \pi $的菱形环路 (a)准一维AB笼菱形晶格示意图; (b)对应$ \pi $通量的声学原胞; (c)两腔耦合时的交叉连接及V形连接; (d)两腔正负耦合的劈裂频率及中心频率随耦合管参数$ {d_1} $的演化; (e)对应$ {{{d_1}} {/ } {{d_0}}} $= 1.6时两种耦合结构的本征模式声压分布; (f)对应于菱形环路中$ 0 $和$ \pi $通量的声学原胞体能带
Figure 1. Rhombic loop with gauge flux $ \pi $; (a) Schematic of quasi-one-dimensional rhombic lattice. (b) acoustic unit cell with gauge flux $ \pi $; (c) cross and V-shaped connections in two coupled cavities; (d) the split eigenfrequencies and central frequency as a function of the tube parameter $ {d_1} $ for the two cavity structures with positive and negative couplings; (e) eigen-pressure patterns for the two structures, exemplified with $ {{{d_1}} {/ } {{d_0}}} $= 1.6; (f) acoustic band structures for $ 0 $ and $ \pi $fluxes in the rhombic loops.
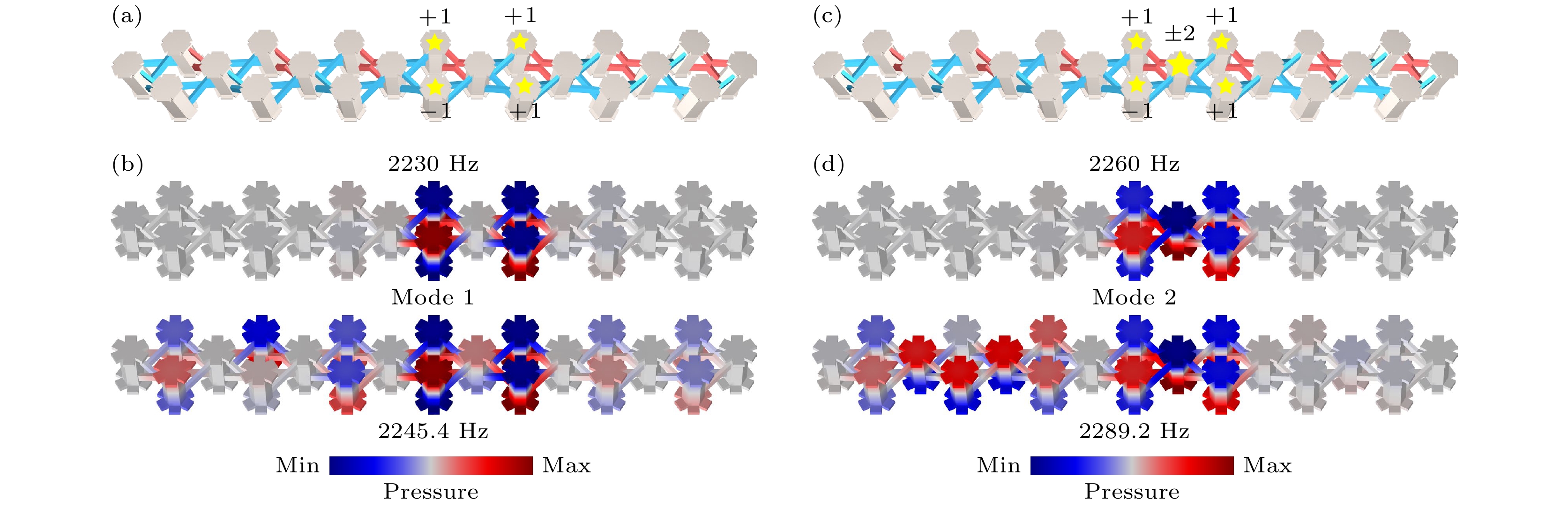
图 2 声学AB笼晶格中的平带态 (a)对应图1(f)第二条平带的本征激发; (b)在图(a)激发条件下的声学平带局域态和平带扩展态; (c)对应图1(f)第三条平带的本征激发; (d)在图(c)激发条件下的声学平带局域态和平带扩展态
Figure 2. Flat band states in acoustic AB cage: (a) Intrinsic excitation for the second flat band in Fig. 1(f); (b) acoustic flat band bound state and flat band diffusion state under the case in Fig. 2(a). (c) intrinsic excitation for the third flat band in Fig. 1(f); (d) acoustic flat band bound state and flat band diffusion state under the case in Fig. 2(c).
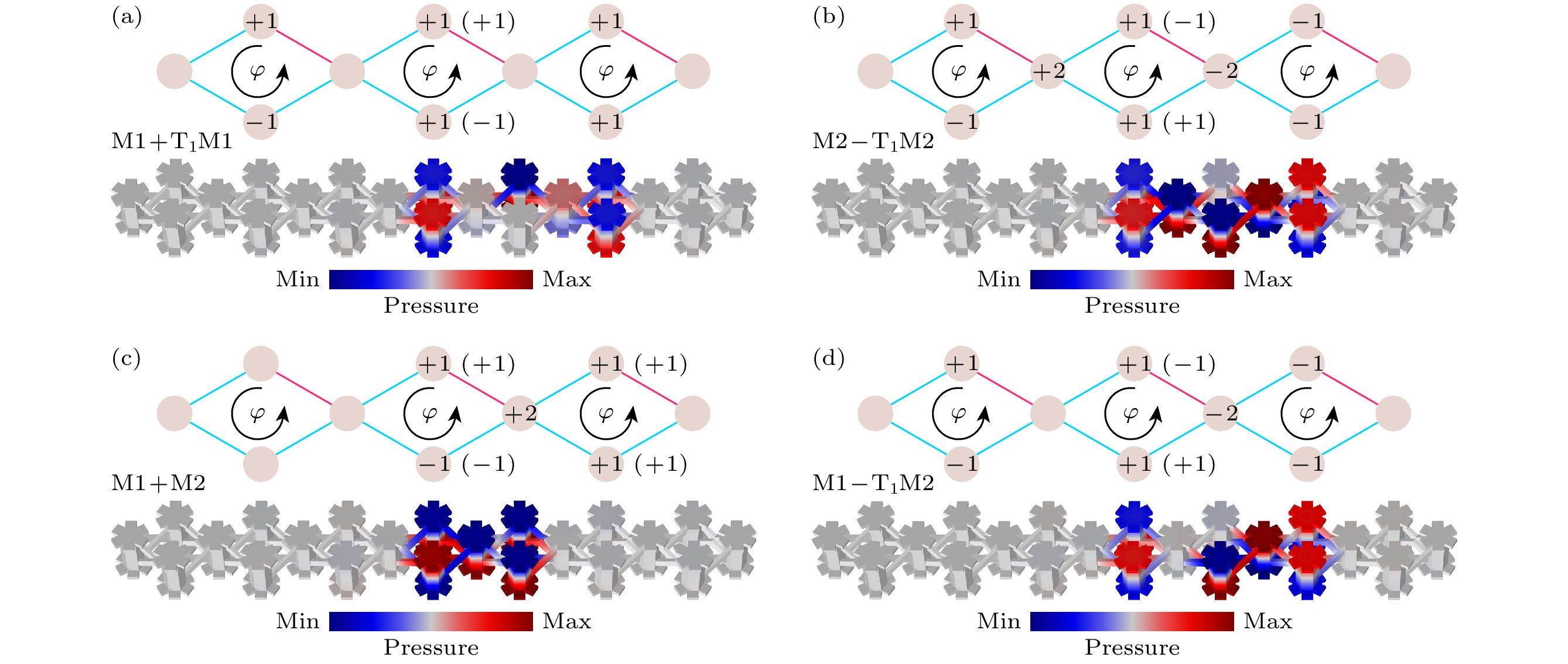
图 3 声学AB笼晶格中复合的平带局域态 (a)基于模式M1叠加的平带局域态, 其中T1表示将局域模式沿基矢方向平移一个晶胞; (b)基于模式M2叠加的平带局域态; (c), (d)模式M1和M2叠加的平带局域态
Figure 3. Composite flat band bound states in acoustic AB cage: (a) Composite flat band bound state based on the flat band bound state M1, and T1 represents the translation of the localized mode along the basis vector by one unit cell; (b) composite flat band bound state based on the flat band bound state M2; (c), (d) composite flat band bound states formed by the superposition of modes M1 and M2.
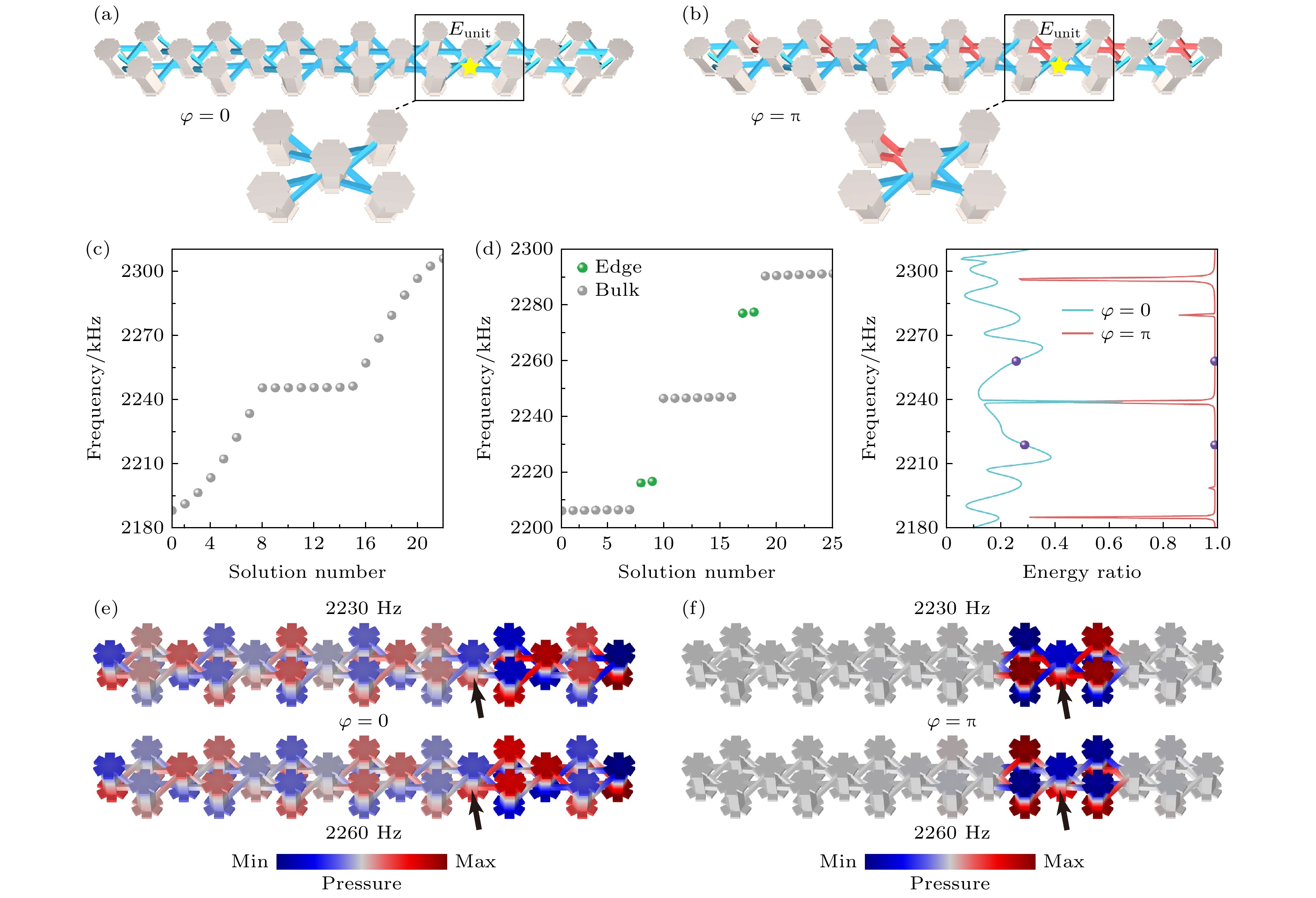
图 4 $ \varphi = 0 $和$ \varphi = \pi $两种有限晶格中的体激发声场分布 (a)通量为0的平庸晶格及体激发声源; (b)通量为$ \pi $的拓扑晶格及体激发声源, 其中黑框为选取的基准局域单元, 黄色星形标记声源激发位置; (c)对应$ \varphi = 0 $有限晶格的本征模式谱图; (d)对应$ \varphi = \pi $有限晶格的本征模式谱图, 其中绿球表示边界态. 右侧版面: 不同参数的$ {{{E_{{\text{unit}}}}} {/ } {{E_{{\text{sys}}}}}} $能量比率图, 紫球为选取的激发频率位置; (e)在2230和2260 Hz, $ \varphi = 0 $菱形晶格中扩展态的场分布; (f)在2230和2260 Hz, $ \varphi = \pi $菱形晶格中的局域声场
Figure 4. Sound field distributions excited at the bulks of two finite lattices with $ \varphi = 0 $ and $ \varphi = \pi $: (a) Schematic of trivial lattice with gauge flux 0 and sound source for bulk excitation; (b) schematic of topological lattice with gauge flux $ \pi $ and sound source for bulk excitation. The black box represents for the selected standard area for sound localization, and the yellow star marks the excitation position of the sound source; (c) eigenfrequencies of the finite rhombic lattice with $ \varphi = 0 $; (d) eigenfrequencies of the finite rhombic lattice with $ \varphi = \pi $, where the green spheres represent the edge states. Right panel: Comparison of the energy ratios $ {{{E_{{\text{unit}}}}} {/ } {{E_{{\text{sys}}}}}} $ for different structures, and the purple spheres indicate the positions of the selected excitation frequencies; (e) the field distributions of diffuse states at 2230 and 2260 Hz under the rhombic lattice with $ \varphi = 0 $; (f) the localized sound fields at 2230 and 2260 Hz under the rhombic lattice with $ \varphi = \pi $.
图 5 $ \varphi = 0 $和$ \varphi = \pi $两种有限晶格中的边界激发声场分布 (a) 0通量有限晶格中的边界激发示意图; (b) $ \pi $通量有限晶格中的边界激发示意图; (c)两种通量参数的能量比率曲线, 紫球为选取的激发频率位置; (d)在2216.8和2277 Hz, $ \varphi = 0 $有限晶格中的扩展态声场; (e)在2216.8和2277 Hz, $ \varphi = {\text{π}} $有限晶格中的边界局域声场; (f)在2204, 2245和2289 Hz, $ \varphi = \pi $有限晶格中的扩散声场
Figure 5. Sound field distributions excited at the edges of two finite lattices with $ \varphi = 0 $ and $ \varphi = \pi $: (a) Schematic of the edge excitation for the finite lattice with flux $ \varphi = 0 $; (b) schematic of the edge excitation for the finite lattice with flux $ \varphi = \pi $; (c) the energy ratio versus the two types of gauge fluxes, and the purple spheres indicate the positions of the selected excitation frequencies; (d) the sound fields of diffuse states at 2216.8 and 2277 Hz under the finite lattice with $ \varphi = 0 $; (e) the edge localized sound fields at 2216.8 and 2277 Hz under the finite lattice with $ \varphi = \pi $; (f) the diffuse sound fields at 2204, 2245 and 2289 Hz under the finite lattice with $ \varphi = \pi $.
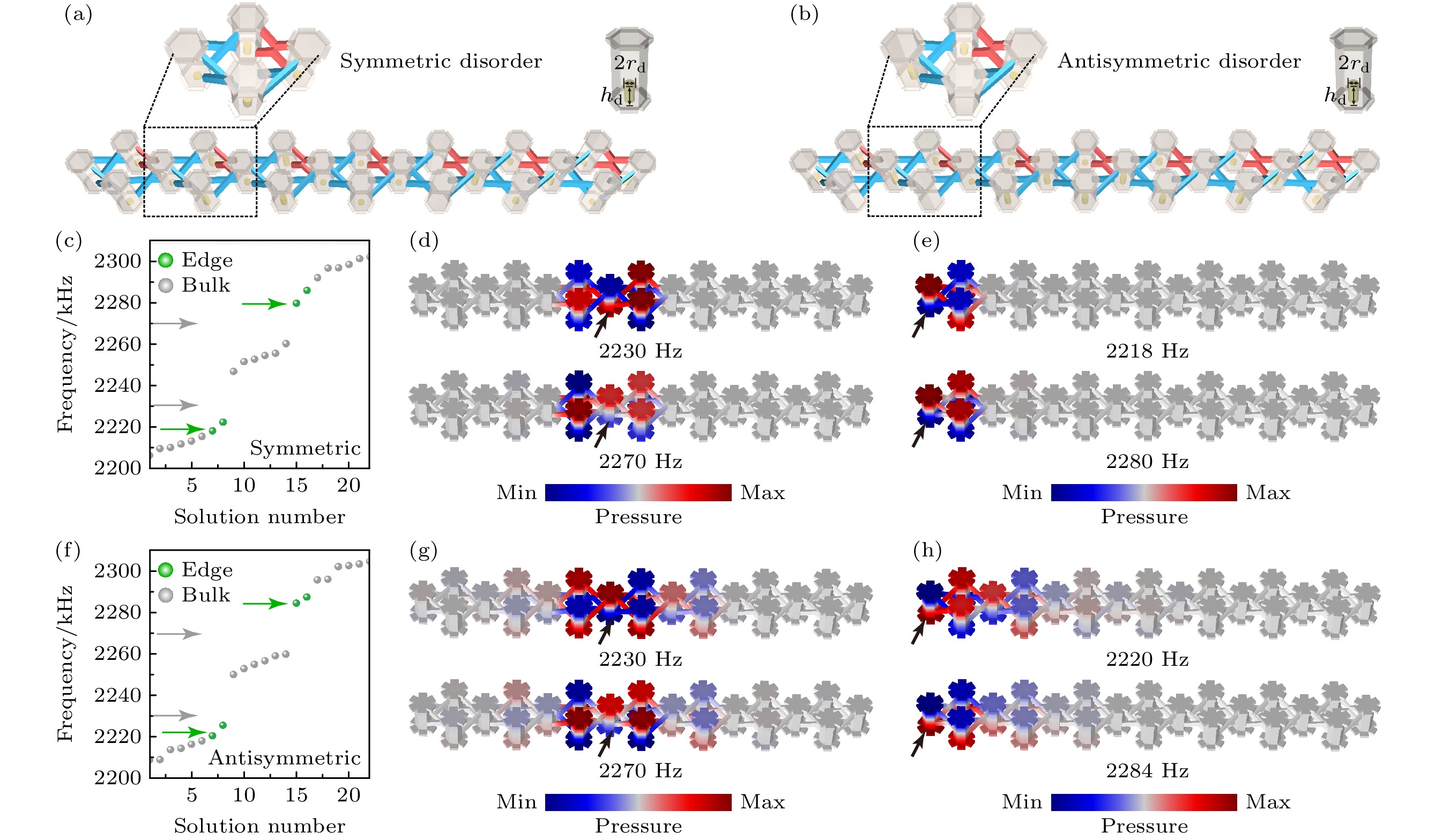
图 6 两种类型结构微扰对AB-笼效应诱导的局域声场的影响 (a)对称类型结构微扰示意图; (b)反对称类型结构微扰示意图; (c)对称微扰结构的本征频谱; (d)在2230和2270 Hz, 对称微扰结构中体激发的局域声场; (e)在2218和2280 Hz, 对称微扰结构中边界激发的拓扑边界局域态; (f)反对称微扰结构的本征频谱; (g)在2230和2270 Hz, 反对称微扰结构中体激发的非局域声场; (h)在2220和2284 Hz, 反对称微扰结构中边界激发的非局域声场
Figure 6. The influence of two types of structural perturbations on acoustic localizations induced by AB-cage effect: (a) Schematic of symmetric structure disorder; (b) schematic of antisymmetric structure disorder; (c) eigenfrequencies for the finite lattice with symmetric disorder; (d) the localized sound fields at 2230 and 2270 Hz excitated in the bulk of the finite lattice with symmetric disorder; (e) the topological edge localized states at 2218 and 2280 Hz excitated at the edge of the finite lattice with symmetric disorder; (f) eigenfrequencies for the finite lattice with antisymmetric disorder; (g) the non-localized sound fields at 2230 and 2270 Hz excitated in the bulk of the finite lattice with antisymmetric disorder; (h) the non-localized sound fields at 2220 and 2284 Hz excitated at the edge of the finite lattice with antisymmetric disorder.
-
[1] Wang X, Sun H, Chen T, Wang X 2019 Phys. Lett. A 383 125918
Google Scholar
[2] Jo S H, Yoon H, Shin Y C, Kim M, Youn B D 2020 J. Appl. Phys. 127 164901
Google Scholar
[3] Jia B, Huang L, Pilipchuk A S, Huang S, Shen C, Sadreev A F, Li Y, Miroshnichenko A E 2023 Phys. Rev. Appl. 19 054001
Google Scholar
[4] Yin Y, Duan Q, Zhu S, Li J, Xie Z, Qiu C W, Chen H 2024 Phys. Rev. B 110 054201
[5] Vaidya S, Benalcazar W A, Cerjan A, Rechtsman M C 2021 Phys. Rev. Lett. 127 023605
Google Scholar
[6] Mukherjee S, Thomson R R 2015 Opt. Lett. 40 5443
Google Scholar
[7] Mukherjee S, Spracklen A, Choudhury D, Goldman N, Öhberg P, Andersson E, Thomson R R 2015 Phys. Rev. Lett. 114 245504
Google Scholar
[8] Vicencio R A, Cantillano C, Morales-Inostroza L, Real B, Mejía-Cortés C, Weimann S, Szameit A, Molina M I 2015 Phys. Rev. Lett. 114 245503
Google Scholar
[9] Shen Y X, Peng Y G, Cao P C, Li J, Zhu X F 2022 Phys. Rev. B 105 104102
Google Scholar
[10] Weaver R L 1990 Wave Motion 12 129
Google Scholar
[11] Dhillon J, Bozhko A, Walker E, Neogi A, Krokhin A 2021 J. Appl. Phys. 129 134701
Google Scholar
[12] Zhang W, Zou D, Pei Q, He W, Bao J, Sun H, Zhang X 2021 Phys. Rev. Lett. 126 146802
Google Scholar
[13] Li S F, Zhou C Y Y, Lu J Y, Zou X Y, Cheng J C 2022 AIP Adv. 12 095111
Google Scholar
[14] Gu Z M, Gao H, Xue H R, Wang D, Guo J M, Su Z Q, Zhang B L, Zhu J 2023 Sci. Chin. Phys. , Mech. Astron. 66 294311
Google Scholar
[15] Liu L, Li T, Zhang Q, Xiao M, Qiu C 2023 Phys. Rev. Lett. 130 106301
Google Scholar
[16] Zhang H Y, Liu S, Guo Z W, Hu S Y, Chen Y G, Li Y H, Li Y, Chen H 2023 Sci. Chin. Phys. , Mech. Astron. 66 284311
Google Scholar
[17] Guo J, Gu Z, Zhu J 2024 Phys. Rev. Lett. 133 236603
Google Scholar
[18] Xue H, Yang Y, Gao F, Chong Y, Zhang B 2019 Nat. Mater. 18 108
Google Scholar
[19] Zhang X, Xie B Y, Wang H F, Xu X, Tian Y, Jiang J H, Lu M H, Chen Y F 2019 Nat. Commun. 10 5331
Google Scholar
[20] Li J, Deng C, Huang Z, Huang J, Wang X, Yang H 2024 Phys. Rev. Appl. 22 054039
Google Scholar
[21] Benalcazar W A, Li T, Hughes T L 2019 Phys. Rev. B 99 245151
Google Scholar
[22] Ye C, Chen Z, Geng Z G, Shen Y X, Zhu X F 2024 Appl. Phys. Lett. 124 182202
Google Scholar
[23] Qi Y, Qiu C, Xiao M, He H, Ke M, Liu Z 2020 Phys. Rev. Lett. 124 206601
Google Scholar
[24] Xue H, Wang Z, Huang Y X, Cheng Z, Yu L, Foo Y X, Zhao Y X, Yang S A, Zhang B 2022 Phys. Rev. Lett. 128 116802
Google Scholar
[25] Li T, Du J, Zhang Q, Li Y, Fan X, Zhang F, Qiu C 2022 Phys. Rev. Lett. 128 116803
Google Scholar
[26] Li T, Liu L, Zhang Q, Qiu C 2023 Commun. Phys. 6 268
Google Scholar
[27] Meng Y, Lin S, Shi B j, Wei B, Yang L, Yan B, Zhu Z, Xi X, Wang Y, Ge Y, Yuan S Q, Chen J, Liu G G, Sun H X, Chen H, Yang Y, Gao Z 2023 Phys. Rev. Lett. 130 026101
Google Scholar
[28] Pu Z, He H, Deng W, Huang X, Ye L, Lu J, Ke M, Liu Z 2023 Phys. Rev. B 108 L220101
Google Scholar
[29] Xiang X, Gao F, Peng Y G, Wu P, Li Z L, Zhu X F 2024 Sci. Chin. Phys. , Mech. Astron. 68 214312
[30] Xiang X, Peng Y G, Gao F, Wu X, Wu P, Chen Z, Ni X, Zhu X F 2024 Phys. Rev. Lett. 132 197202
Google Scholar
[31] Chen S, Ke S, Zhao D, Ye J, Wang Y, Liu W, Huang K, Wang B, Lu P 2024 Nano Lett. 24 4810
[32] Yan M, Huang X, Luo L, Lu J, Deng W, Liu Z 2020 Phys. Rev. B 102 180102
Google Scholar
[33] Geng Z G, Shen Y X, Duan L, Chen Z, Zhu X F 2023 J. Phys. Condens. Matter 35 405001
Google Scholar
[34] Wu S Q, Lin Z K, Xiong Z, Jiang B, Jiang J H 2023 Phys. Rev. Appl. 19 024023
Google Scholar
[35] Longhi S 2014 Opt. Lett. 39 5892
Google Scholar
[36] Kremer M, Petrides I, Meyer E, Heinrich M, Zilberberg O, Szameit A 2020 Nat. Commun. 11 907
Google Scholar
DownLoad:
Metrics
- Abstract views: 284
- PDF Downloads: 8
- Cited By: 0
