-
Control parameters are frequently subjected to certain restrictions in the engineering practice of chaos control. It is difficult to stabilize multi-rotation unstable periodic trajectory when the stability range is too small and outside the restrictions of control parameters. Thus, it is fundamentally important to expand the stability range of the controlled multi-rotation unstable periodic trajectory by using an applicable method. In this work, the original extended time-delay feedback control is improved based on the time-varying switching strategy, which leads to the time-varying switching extended time-delay feedback control. The time-varying switching extended time-delay feedback control only applies the control to the controlled system in a specific period, and does not apply the control to it in other periods, this is different from the continuous control of the original extended time-delay feedback control. The specific performance of the time-varying switching extended time-delay feedback control in stabilizing unstable multi-rotation periodic trajectories is investigated by case studies. The maximum Floquet multiplier of the controlled periodic trajectory is calculated, and the relationship between the stability region of the controlled multi-rotation periodic trajectory and the switching frequency is obtained. The results show that with the increase of switching frequency, the stability region of the controlled multi-rotation periodic trajectory presents a non-smooth change. In particular, the stability region of the time-varying switching extended time-delay feedback control is significantly larger than that of the original extended time-delay feedback control when an appropriate switching frequency is selected.
-
Keywords:
- chaos control /
- delayed feedback /
- periodic trajectory /
- Floquet multipliers
[1] 石航, 王丽丹 2019 68 200501
Google Scholar
Shi H, Wang L D 2019 Acta Phys. Sin. 68 200501
Google Scholar
[2] 孔江涛, 黄健, 龚建兴, 李尔玉 2018 67 098901
Google Scholar
Kong J T, Huang J, Gong J X, Li E Y 2018 Acta Phys. Sin. 67 098901
Google Scholar
[3] 秦铭宏, 赖强, 吴永红 2022 71 160502
Google Scholar
Qin M H, Lai Q, Wu Y H 2022 Acta Phys. Sin. 71 160502
Google Scholar
[4] Lima R, Pettini M 1990 Phys. Rev. A 41 726
Google Scholar
[5] Braiman Y, Goldhirsch I 1991 Phys. Rev. Lett. 66 2545
Google Scholar
[6] Lathrop D P, Kostelich E J 1989 Phys. Rev. A 40 4028
Google Scholar
[7] Ott E, Grebogi C, Yorke J A 1990 Phys. Rev. Lett. 64 1196
Google Scholar
[8] Pyragas K 1992 Phys. Lett. A 170 421
Google Scholar
[9] Mitra R K, Banik A K, Chatterjee S 2018 J. Comput. Nonlin. Dyn. 13 031001
Google Scholar
[10] Kuznetsov N V, Leonov G A, Shumafov M M 2015 IFAC-PapersOnLine 48 706
Google Scholar
[11] 张士荣, 赵俊杰, 谈发明 2022 激光杂志 43 154
Google Scholar
Zhang S R, Zhao J J, Tan F M 2022 Laser J. 43 154
Google Scholar
[12] Pyragas K, Novičenko V 2013 Phys. Rev. E 88 12903
[13] Hu H Y 2004 J. Sound Vib. 275 1009
Google Scholar
[14] Nakajima H 1997 Phys. Lett. A 232 207
Google Scholar
[15] Amann A, Hooton E W 2013 Philos. T. R. Soc. A 371 0120463
[16] Pyragas K 2001 Phys. Rev. Lett. 86 2265
Google Scholar
[17] 颜森林 2021 70 080501
Google Scholar
Yan S L 2021 Acta Phys. Sin. 70 080501
Google Scholar
[18] Zheng Y G, Zhang Y Y 2021 J. Franklin I. 358 1240
Google Scholar
[19] Pyragas K 1995 Phys. Lett. A 206 323
Google Scholar
[20] De Paula A S, Savi M A 2009 ISO4. 42 2981
[21] Robert B, Feki M, Iu H H 2006 Int. J. Bifurcat. Chaos 16 113
Google Scholar
[22] Banerjee T, Sarkar B C 2012 Int. J. Bifurcat. Chaos 22 1230044
Google Scholar
[23] Zheng Y G, Zhang Y Y 2021 Commun. Nonlinear. Sci. 98 105788
Google Scholar
[24] Schröder M, Mannattil M, Dutta D, Chakraborty S, Timme M 2015 Phys. Rev. Lett. 115 054101
Google Scholar
[25] Tandon A, Schröder M, Mannattil M, Timme M, Chakraborty S 2016 Chaos 26 094817
Google Scholar
[26] Li S, Sun N, Chen L, Wang X 2018 Phys. Rev. E 98 012304
[27] Ghosh A, Godara P, Chakraborty S 2018 Chaos 28 053112
Google Scholar
[28] Buscarino A, Frasca M, Branciforte M, Fortuna L, Sprott J C 2017 Nonlinear Dynam. 88 673
Google Scholar
[29] Socolar J E, Sukow D W, Gauthier D J 1994 Phys. Rev. E 50 3245
[30] Eckhardt B, Yao D 1993 Physica D 65 100
Google Scholar
-
图 1 Duffing系统的混沌吸引子
Figure 1. The chaotic attractor of Duffing system.
图 2 Duffing系统的多旋转周期轨线
$ {\hat X_2}(t) $ 在 xoy 平面上的投影Figure 2. The projection of the high-period UPO
$ {\hat X_2}(t) $ with period-2 circles of Duffing system on the xoy plane.
图 3 系统(10)式的时间序列和TSEDFC控制在不同时段上切换示意图, 在灰色时段施加控制, 而在灰色时段外不施加控制
Figure 3. The time series of system (10) and the schematic diagram of the switching of TSEDFC control signals in different time intervals, where the control signal exists in the gray time intervals and disappears outside the gray time intervals.
图 4 受控多旋转周期轨线
$ {\hat X_2}(t) $ 的稳定区域随切换频率$ \omega $ 的变化曲线, 其中稳定域是蓝色区域, Floquet乘数的最大幅度小于1Figure 4. The relationships between the stable domain of the controlled high-period UPO
$ {\hat X_2}(t) $ and switching frequency$ \omega $ , where the stable domain is the blue region and the largest magnitude of the Floquet multipliers is less than one.
图 5 受控多旋转周期轨线
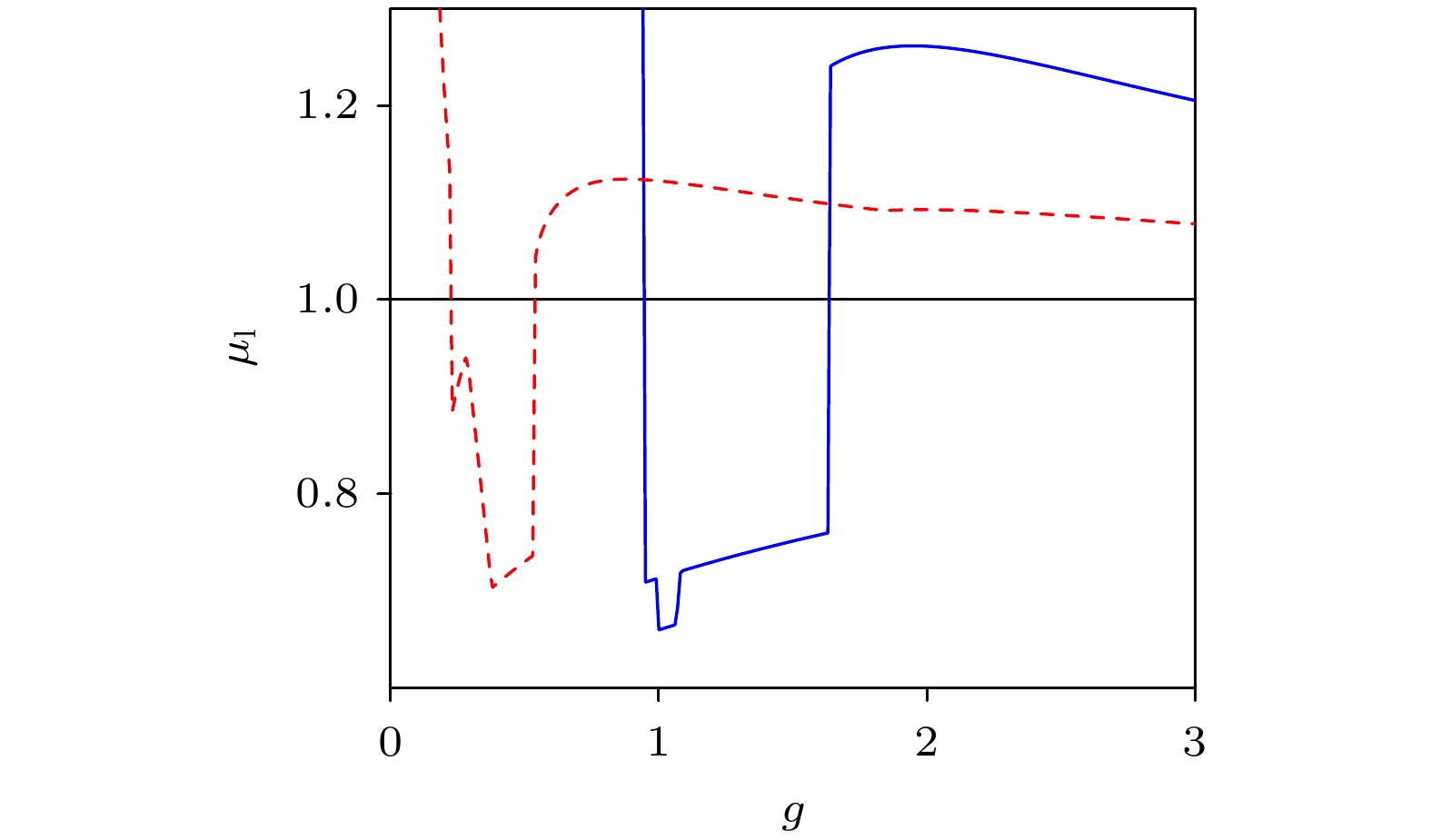
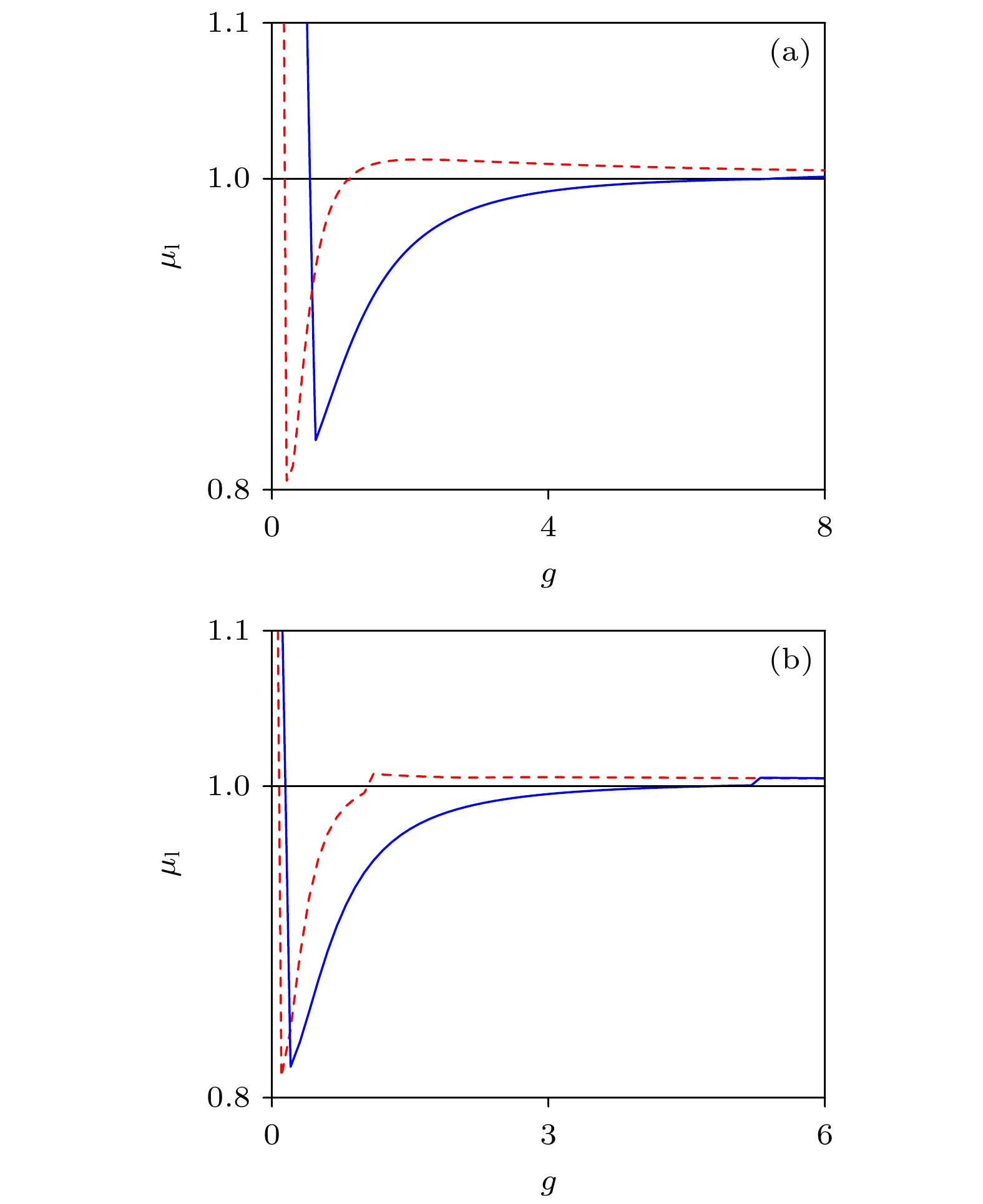
$ {\hat X_2}(t) $ 的最大Floquet乘数随反馈增益系数$ g $ 的变化曲线对比图, 红色虚线和蓝色实线分别对应于EDFC和TSEDFCFigure 5. The largest magnitudes of the Floquet multipliers of the controlled high-period UPO
$ {\hat X_2}(t) $ as functions of the feedback gain$ g $ . The red dashed lines and blue solid lines correspond to EDFC and TSEDFC, respectively
图 6 受控多旋转周期轨线
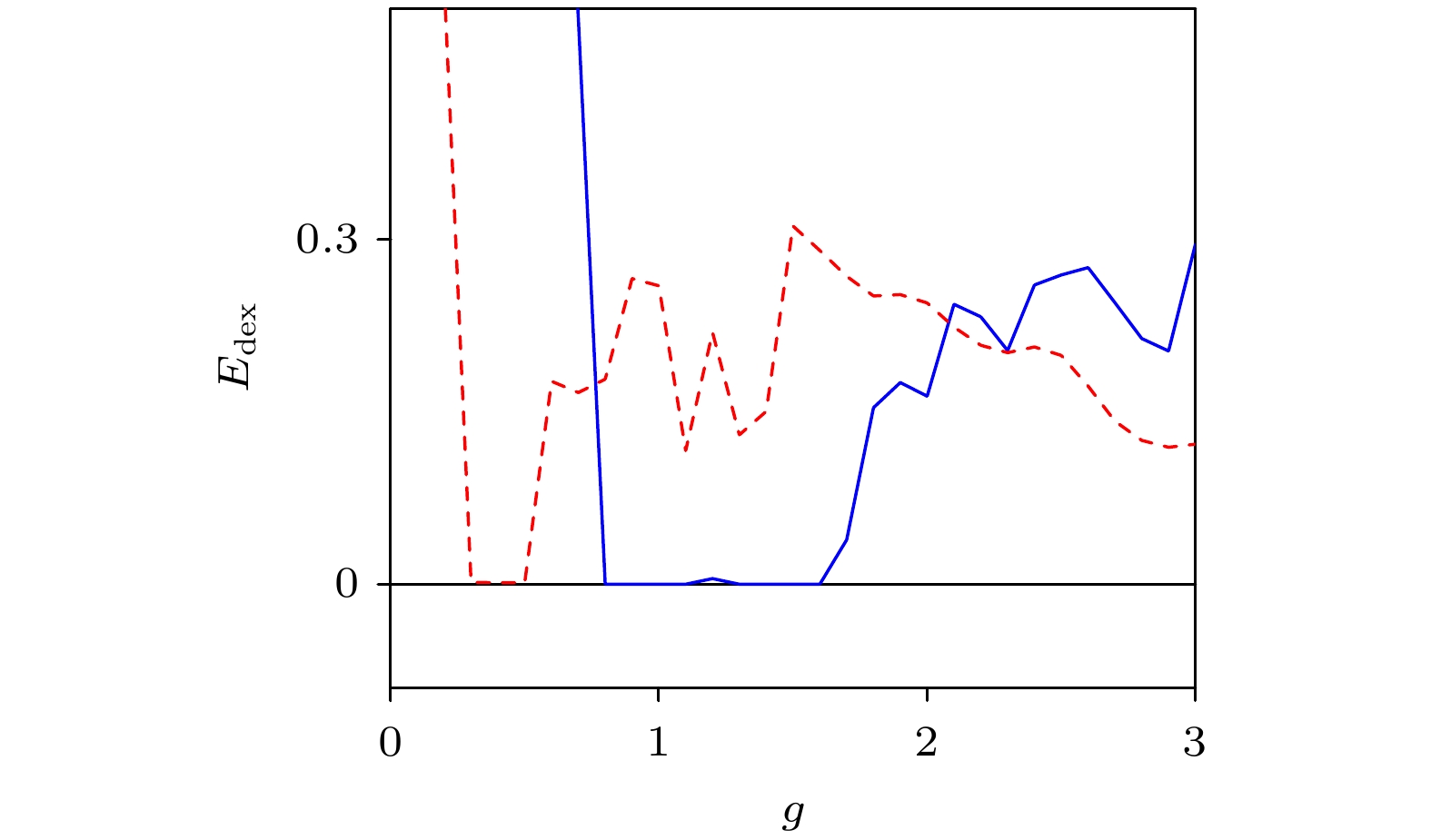
$ {\hat X_2}(t) $ 的误差指数$ {E_{{\text{dex}}}} $ 随反馈增益系数$ g $ 的变化曲线对比图, 红色虚线和蓝色实线分别对应于EDFC和TSEDFCFigure 6. The error indices
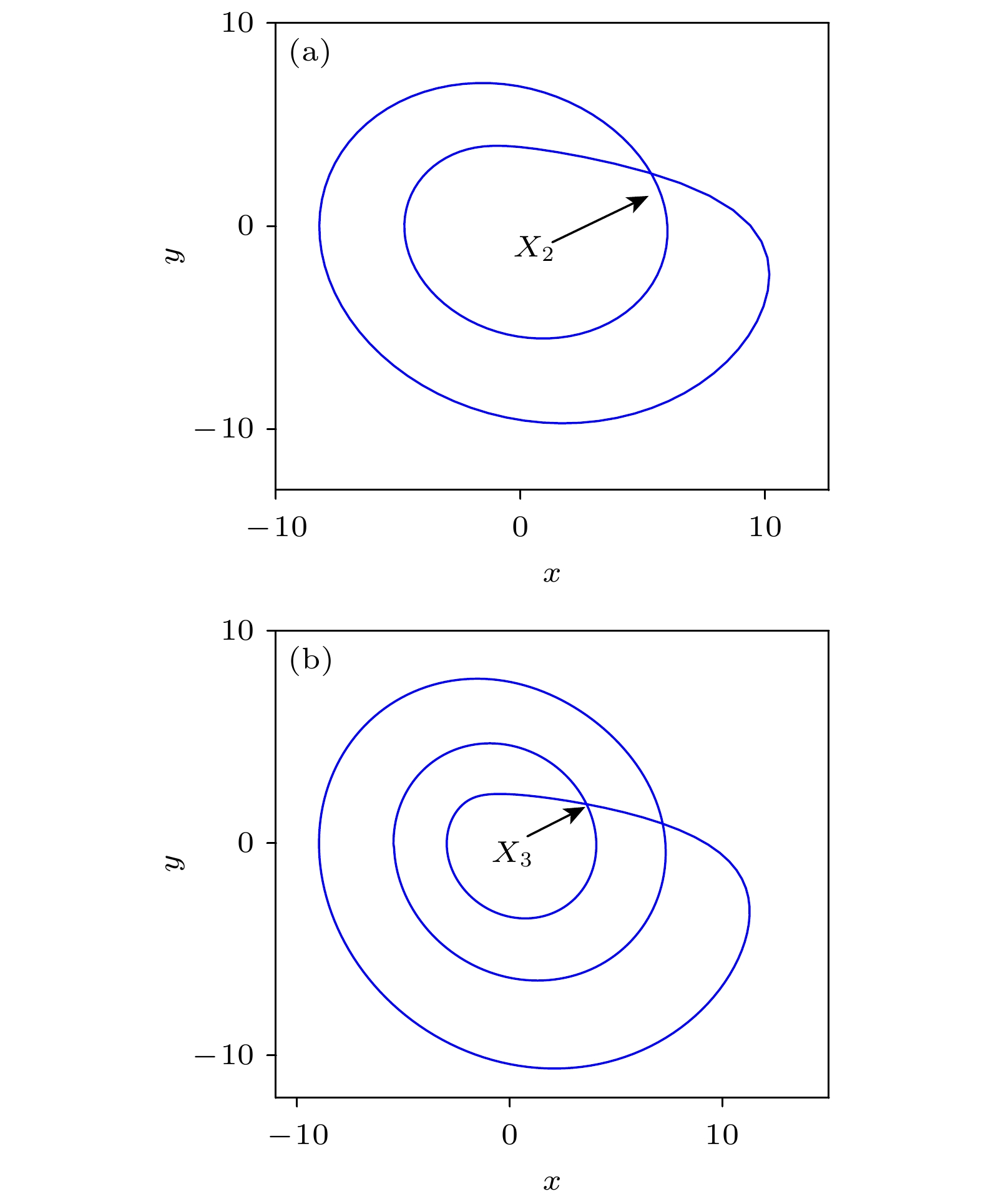
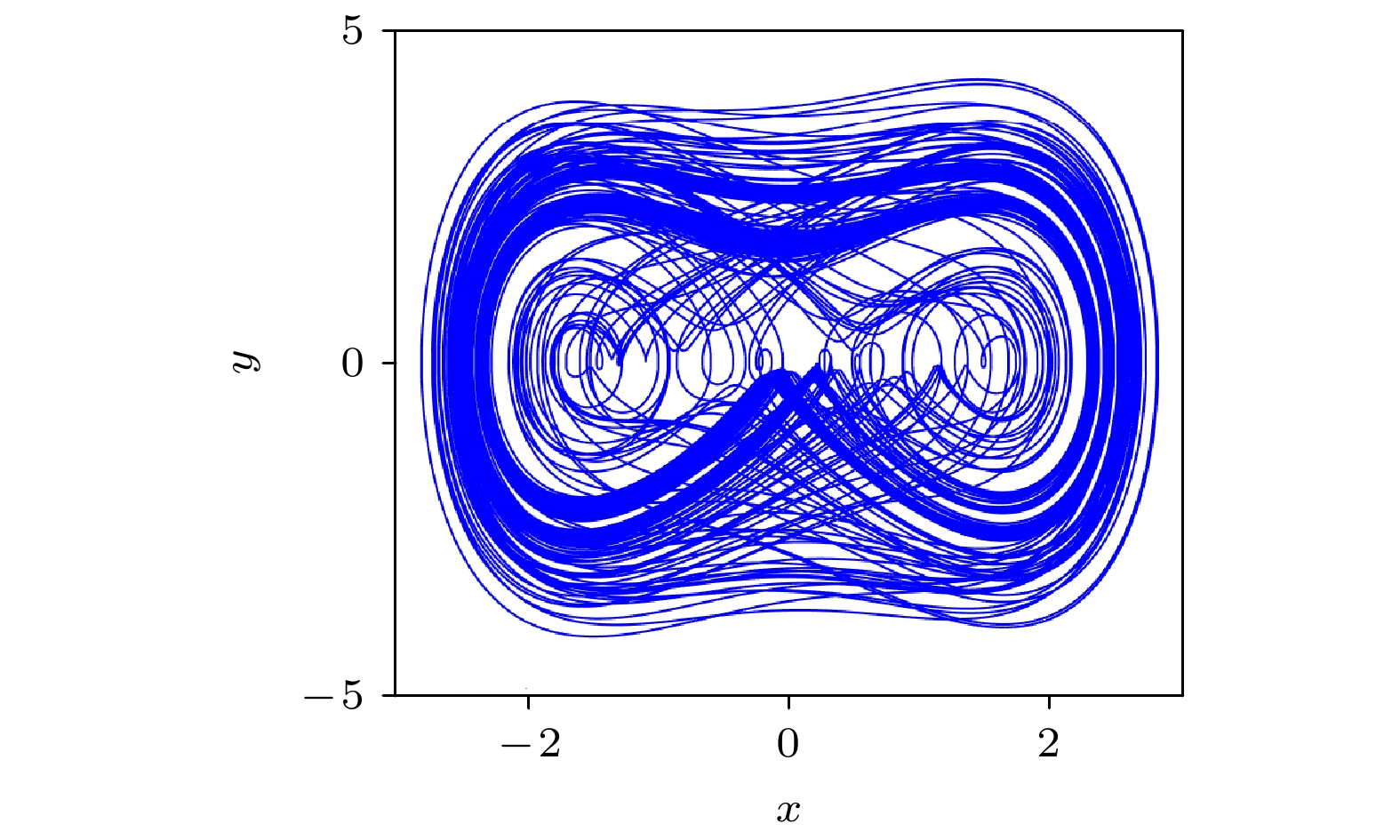
$ {E_{{\text{dex}}}} $ of the controlled high-period UPO$ {\hat X_2}(t) $ as functions of the feedback gain$ g $ . The red dashed lines and blue solid lines correspond to EDFC and TSEDFC, respectively
图 7 Röossler系统的混沌吸引子
Figure 7. The chaotic attractor of Röossler system.
图 8 Röossler系统的不稳定多旋转周期轨线在
$ xoy $ 平面上的投影 (a)多旋转周期轨线$ {X_2}(t) $ ; (b)多旋转周期轨线$ {X_3}(t) $ Figure 8. The projection of the high-period UPO
$ {X_k}(t) $ with period-k circles of Röossler system on the$ xoy $ plane: (a) The high-period UPO$ {X_2}(t) $ with period-2 circles; (b) the high-period UPO$ {X_3}(t) $ with period-3 circles.
图 9 受控多旋转周期轨线
$ {X_k}(t) $ 的稳定区域随切换频率$ \omega $ 的变化曲线，其中稳定区域是蓝色区域，Floquet乘数的最大幅度小于1 (a) 受控多旋转周期轨线$ {X_2}(t) $ ; (b) 受控多旋转周期轨线$ {X_3}(t) $ Figure 9. The relationships between the stable domain of the controlled high-period UPOs
$ {X_k}(t) $ and the switching frequency$ \omega $ , where the stable domain is the gray region where the largest magnitude of the Floquet multipliers is less than one: (a) The projection of the controlled high-period UPO$ {X_2}(t) $ with period-2 circles; (b) the projection of the controlled high-period UPO$ {X_3}(t) $ with period-3 circles.
图 10 受控多旋转周期轨线
$ {X_k}(t) $ 的最大Floquet乘数随反馈增益系数$ g $ 的变化曲线对比图, 红色虚线和蓝色实线分别对应于EDFC和TSEDFC (a) 受控多旋转周期轨线$ {X_2}(t) $ ; (b)受控多旋转周期轨线$ {X_3}(t) $ Figure 10. The largest magnitudes of the Floquet multipliers of the controlled high-period UPOs
$ {X_k}(t) $ as functions of the feedback gain$ g $ . The red dashed lines and blue solid lines correspond to EDFC and TSEDFC, respectively: (a) The projection of the controlled high-period UPO$ {X_2}(t) $ with period-2 circles; (b) the projection of the controlled high-period UPO$ {X_3}(t) $ with period-3 circles.
图 11 受控多旋转周期轨线
$ {X_k}(t) $ 的误差指数$ {E_{{\text{dex}}}} $ 随反馈增益系数$ g $ 的变化曲线对比图, 红色虚线和蓝色实线分别对应于EDFC和TSEDFC (a) 受控多旋转周期轨线$X_2(t) $ ; (b) 受控多旋转周期轨线$X_3(t) $ Figure 11. The error indices
$ {E_{{\text{dex}}}} $ of the controlled high-period UPO$ {X_k}(t) $ as functions of the feedback gain$ g $ . The red dashed lines and blue solid lines correspond to EDFC and TSEDFC, respectively: (a) The projection of the controlled high-period UPO$X_2(t) $ with period-2 circles; (b) the projection of the controlled high-period UPO$X_3(t) $ with period-3 circles. -
[1] 石航, 王丽丹 2019 68 200501
Google Scholar
Shi H, Wang L D 2019 Acta Phys. Sin. 68 200501
Google Scholar
[2] 孔江涛, 黄健, 龚建兴, 李尔玉 2018 67 098901
Google Scholar
Kong J T, Huang J, Gong J X, Li E Y 2018 Acta Phys. Sin. 67 098901
Google Scholar
[3] 秦铭宏, 赖强, 吴永红 2022 71 160502
Google Scholar
Qin M H, Lai Q, Wu Y H 2022 Acta Phys. Sin. 71 160502
Google Scholar
[4] Lima R, Pettini M 1990 Phys. Rev. A 41 726
Google Scholar
[5] Braiman Y, Goldhirsch I 1991 Phys. Rev. Lett. 66 2545
Google Scholar
[6] Lathrop D P, Kostelich E J 1989 Phys. Rev. A 40 4028
Google Scholar
[7] Ott E, Grebogi C, Yorke J A 1990 Phys. Rev. Lett. 64 1196
Google Scholar
[8] Pyragas K 1992 Phys. Lett. A 170 421
Google Scholar
[9] Mitra R K, Banik A K, Chatterjee S 2018 J. Comput. Nonlin. Dyn. 13 031001
Google Scholar
[10] Kuznetsov N V, Leonov G A, Shumafov M M 2015 IFAC-PapersOnLine 48 706
Google Scholar
[11] 张士荣, 赵俊杰, 谈发明 2022 激光杂志 43 154
Google Scholar
Zhang S R, Zhao J J, Tan F M 2022 Laser J. 43 154
Google Scholar
[12] Pyragas K, Novičenko V 2013 Phys. Rev. E 88 12903
[13] Hu H Y 2004 J. Sound Vib. 275 1009
Google Scholar
[14] Nakajima H 1997 Phys. Lett. A 232 207
Google Scholar
[15] Amann A, Hooton E W 2013 Philos. T. R. Soc. A 371 0120463
[16] Pyragas K 2001 Phys. Rev. Lett. 86 2265
Google Scholar
[17] 颜森林 2021 70 080501
Google Scholar
Yan S L 2021 Acta Phys. Sin. 70 080501
Google Scholar
[18] Zheng Y G, Zhang Y Y 2021 J. Franklin I. 358 1240
Google Scholar
[19] Pyragas K 1995 Phys. Lett. A 206 323
Google Scholar
[20] De Paula A S, Savi M A 2009 ISO4. 42 2981
[21] Robert B, Feki M, Iu H H 2006 Int. J. Bifurcat. Chaos 16 113
Google Scholar
[22] Banerjee T, Sarkar B C 2012 Int. J. Bifurcat. Chaos 22 1230044
Google Scholar
[23] Zheng Y G, Zhang Y Y 2021 Commun. Nonlinear. Sci. 98 105788
Google Scholar
[24] Schröder M, Mannattil M, Dutta D, Chakraborty S, Timme M 2015 Phys. Rev. Lett. 115 054101
Google Scholar
[25] Tandon A, Schröder M, Mannattil M, Timme M, Chakraborty S 2016 Chaos 26 094817
Google Scholar
[26] Li S, Sun N, Chen L, Wang X 2018 Phys. Rev. E 98 012304
[27] Ghosh A, Godara P, Chakraborty S 2018 Chaos 28 053112
Google Scholar
[28] Buscarino A, Frasca M, Branciforte M, Fortuna L, Sprott J C 2017 Nonlinear Dynam. 88 673
Google Scholar
[29] Socolar J E, Sukow D W, Gauthier D J 1994 Phys. Rev. E 50 3245
[30] Eckhardt B, Yao D 1993 Physica D 65 100
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2958
- PDF Downloads: 55
- Cited By: 0
