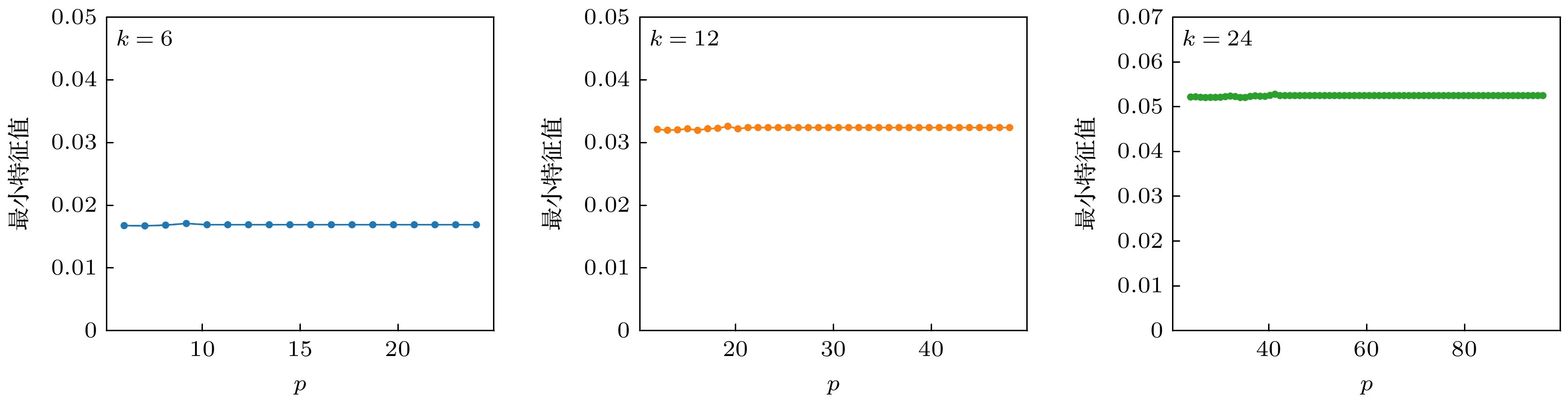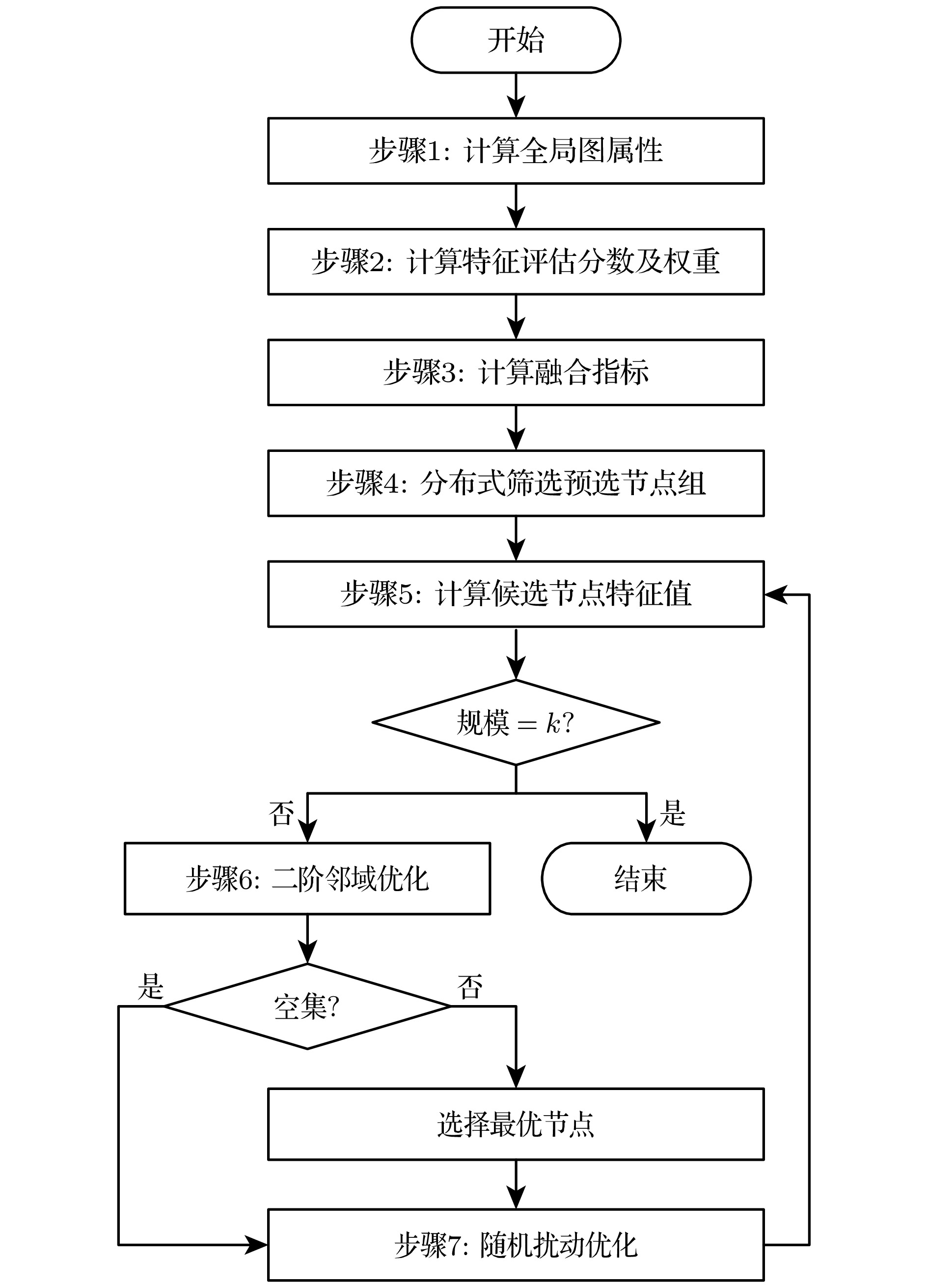
-
本文研究了无向复杂网络中基于谱图理论的节点组重要性挖掘问题. 依据复杂网络牵制控制理论中节点重要性评价指标, 删后Laplacian矩阵最小特征值较大者为重要受控节点. 本文提出一种基于多重图特征线性融合与改进贪心搜索的重要节点组挖掘方法(multi-metric fusion and enhanced greedy search algorithm, MFG算法). 该方法首先通过融合度中心性、介数中心性、K-Shell值和电阻距离等多重指标, 结合全局图特征(如图密度、平均路径长度等)构建线性加权融合模型, 预筛选候选节点组以克服单一指标的局限性; 其次, 设计二阶邻域局部扰动与全局随机游走搜索策略, 优化传统贪心算法的短视性, 在预筛选节点组中迭代选择使得删后Laplacian矩阵最小特征值最大的节点, 从而平衡局部最优与全局搜索能力; 并利用改进的反幂法进行最小特征值的计算, 降低了传统计算特征谱的复杂度, 从而使得算法总体计算性能提升. 最后, 在经典网络模型和多个真实网络中进行仿真分析, 利用不同算法挖掘重要节点组, 计算删后拉普拉斯矩阵的最小特征值, 利用SIR模型进行传播模拟, 并从网络拓扑上分析不同算法筛选出的重要节点组特征. 结果表明MFG算法相比其他几种算法挖掘重要节点组的效果更好, 对于社交网络信息传播控制具有指导意义.
-
关键词:
- 复杂网络 /
- 节点组重要性 /
- 预筛选算法 /
- 删后拉普拉斯矩阵谱图理论
In this paper, we investigate the saliency identification of node groups in undirected complex networks by utilizing spectral graph theory of pinning control. According to the node significance criterion in network pinning control theory, where important controlled nodes are those maximizing the minimum eigenvalue of the grounded Laplacian matrix after their removal, we propose multi-metric fusion and enhanced greedy search algorithm (MFG), a novel key node group identification framework that integrates multi-metric linear fusion and an enhanced greedy search strategy. First, a linear weighted fusion model that synergistically integrates local centrality metrics with global graph properties is constructed to pre-screen potentially more important node groups, effectively reducing the inherent limitations of a single-metric evaluation paradigm. Second, a dual search strategy combining second-order neighborhood perturbation and global random walk mechanisms is developed to optimize the myopic nature of traditional greedy algorithms. Through iterative selection within pre-screened node groups, the nodes maximizing the minimum eigenvalue of the grounded Laplacian matrix are identified, achieving an optimal balance between local optimization and global search capabilities. Third, computational efficiency is enhanced by using a modified inverse power method for eigenvalue calculation, reducing the complexity of traditional spectral computations. Comprehensive simulations of generated networks and real-world networks demonstrate the framework’s superiority. The evaluation of the proposed algorithm includes three aspects: 1) comparison of the minimum eigenvalues between different algorithms; 2) SIR epidemic modeling for propagation capability assessment; 3) topological analysis of identified key nodes. The simulation results reveal the following two significant points: a) Our method outperforms state-of-the-art benchmarks (NPE, AGM, HVGC) in maximizing the ground Laplacian minimum eigenvalue in synthesized (NW small-world, ER) and real-world networks, especially at critical control sizes; b) The identified critical node groups exhibit unique topological features, typically combining high-level hubs with strategically located bridges to best balance local influence and global connectivity. Importantly, the SIR propagation model confirms that these topologically optimized populations accelerate the early outbreak of epidemics and maximize global saturation coverage, directly linking structural features with superior dynamic influence. These findings provide guidance for controlling information propagation in social networks.-
Keywords:
- complex network /
- node group importance /
- pre-screening algorithm /
- spectral graph theory of the grounded Laplacian matrix
[1] Liu H, Xu X H, Lu J A, Chen G R, Zeng Z G 2021 IEEE Trans. Syst. Man Cybern. Syst. 51 786
Google Scholar
[2] 刘慧, 王炳珺, 陆君安, 李增扬 2021 70 056401
Google Scholar
Liu H, Wang B J, Lu J A, Li Z Y 2021 Acta Phys. Sin. 70 056401
Google Scholar
[3] Zhou F, Su C, Xu S Q, Lü L Y 2022 Chin. Phys. B 31 068901
Google Scholar
[4] Dai J Y, Wang B, Sheng J F, Sun Z J, Khawaja F R, Ullah A 2019 IEEE Access 7 131719
Google Scholar
[5] 孔江涛, 黄健, 龚建兴, 李尔玉 2018 67 098901
Google Scholar
Kong J T, Huang J, Gong J X, Li E Y 2018 Acta Phys. Sin. 67 098901
Google Scholar
[6] 汪亭亭, 梁宗文, 张若曦 2023 72 048901
Google Scholar
Wang T T, Lang Z W, Zhang R X 2023 Acta Phys. Sin. 72 048901
Google Scholar
[7] 杨松青, 蒋沅, 童天驰, 严玉为, 淦各升 2021 70 216401
Google Scholar
Yang S Q, Jiang Y, Tong T C, Yan Y W, Gan G S 2021 Acta Phys. Sin. 70 216401
Google Scholar
[8] 姜廷帅, 阮逸润, 李海, 白亮, 袁逸飞, 于天元 2025 74 126401
Google Scholar
Jiang T S, Ruan Y R, Li H, Bai L, Yuan Y F, Yu T Y 2025 Acta Phys. Sin. 74 126401
Google Scholar
[9] Rezaei A A, Munoz J, Jalili M, Khayyam H 2023 Expert Syst. Appl. 214 119086
Google Scholar
[10] Zhang Y H, Lu Y L, Yang G Z, Hang Z J 2022 Appl. Sci. 12 1944
Google Scholar
[11] 王博雅, 杨小春, 卢升荣, 唐勇平, 洪树权, 蒋惠园 2024 73 226401
Google Scholar
Wang B Y, Yang X C, Lu S R, Tang Y P, Hong S Q, Jiang H Y 2024 Acta Phys. Sin. 73 226401
Google Scholar
[12] Lü L Y, Zhou T, Zhang Q M, Stanley H E 2016 Nat. Commun. 7 10168
Google Scholar
[13] Kou J H, Jia P, Liu J Y, Dai J Q, Luo H R 2023 Neurocomputing 530 23
Google Scholar
[14] Qiu Z H, Fan T L, Li M, Lü L Y 2021 New J. Phys. 23 033036
Google Scholar
[15] Chakrabarti S, Dom B, Raghavan P, Rajagopalan S, Gibson D, Kleinberg J 1998 CNIS 30 65
Google Scholar
[16] Fan C J, Zeng L, Sun Y Z, Liu Y Y 2020 Nat. Mach. Intell. 2 317
Google Scholar
[17] Zhao X Y, Huang B, Tang M, Zhang H F, Chen D B 2014 Europhys. Lett. 108 68005
Google Scholar
[18] Bao Z K, Liu J G, Zhang H F 2017 Phys. Lett. A 381 976
Google Scholar
[19] Ji S G, Lü L Y, Yeung C H, Hu Y Q 2017 New J. Phys. 19 073020
Google Scholar
[20] Anderson R M, May R M 1991 Infectious Diseases of Humans: Dynamics and Control (Oxford University Press
[21] Pastor-Satorras R, Castellano C, Mieghem P V, Vespignani A 2015 Rev. Mod. Phys. 87 925
Google Scholar
[22] Feng M L, Zhang S F, Xia C Y, Zhao D W 2024 Chaos 34 073128
Google Scholar
[23] Avraam D, Hadjichrysanthou C 2024 J. Theor. Biol. 599 112010
Google Scholar
[24] Lu J A, Liu H, Chen J 2016 Synchronization in Complex Dynamical Networks (Vol. 1) (Beijing: Higher Education Press) p49
[25] Pirani M, Sundaram S 2016 IEEE Trans. Autom. Control 61 509
Google Scholar
[26] Bapat R B 2010 Graphs and Matrices (Springer London
[27] Zhu H Y, Klein D J, Lukovits I 1996 J. Chem. Inf. Model. 36 420
Google Scholar
[28] Gutman I, Mohar B 1996 J. Chem. Inf. Comput. Sci. 36 982
Google Scholar
[29] 关治, 陈景良 1990 数值计算方法(北京: 清华大学出版社)
Guan Z, Chen J L 1990 Numerical Calculation Method (Beijing: Tsinghua University Press
[30] 刘砚青, 陆君安 2007 复杂系统与复杂性科学 4 13
Liu Y Q, Lu J A 2007 Complex Syst. Complexity Sci. 4 13
[31] Dean J, Ghemawat S 2008 Commun. ACM 51 107
Google Scholar
[32] Yin H, Benson A R, Leskovec J, Gleich D F 2017 Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’17 ) Halifax, NS, Canada, August 13–17, 2017 p555
[33] 吴英晗, 田阔, 李明达, 胡枫 2023 计算机工程与应用 19 66
Google Scholar
Wu Y H, Tian K, Li M D, Hu F 2023 Comput. Appl. Eng. Educ. 19 66
Google Scholar
[34] Meng L, Xu G Q, Dong C 2025 Physica A 657 130237
Google Scholar
[35] Zhu S Q, Zhan J, Li X 2023 Sci. Rep. 13 16404
Google Scholar
[36] Snap: Stanford network analysis project https://snap.stanford.edu/.
[37] Jiang W C, Wang Y H 2020 IEEE Access 8 32432
Google Scholar
-
图 1 一个简单矩阵的电阻距离计算过程
Fig. 1. Process of calculating the resistance distance of a simple matrix.
图 2 ER 随机网络节点的度及电阻距离分别与${\lambda _1}({{\boldsymbol{L}}_{N - 1}})$的排序相关性
Fig. 2. Correlation between the degree of nodes and the resistance distance in ER random networks, respectively, with the ${\lambda _1}({{\boldsymbol{L}}_{N - 1}})$.
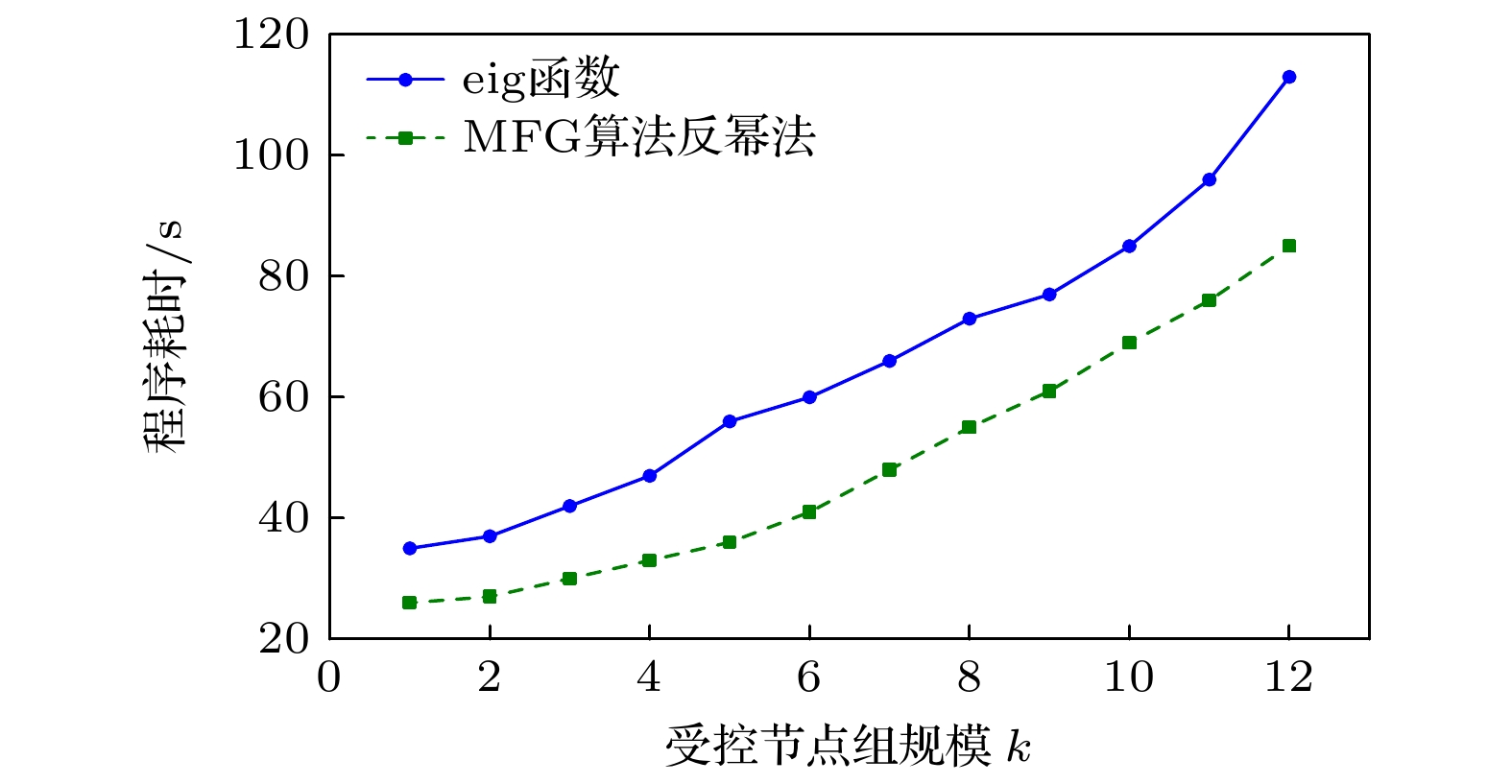
图 4 在E-mail网络中, 取$1 \leqslant k \leqslant 12\left( {k \in \mathbb{Z}} \right)$, $s = 3$, $p = $$ 2 k$时, 使用eig函数和反幂法的程序耗时对比
Fig. 4. In the E-mail network, when taking $1 \leqslant k \leqslant $$ 12\left( {k \in \mathbb{Z}} \right)$, $s = 3$ and $p = 2 k$, the comparison of the computational time between the eig function and the inverse power method.
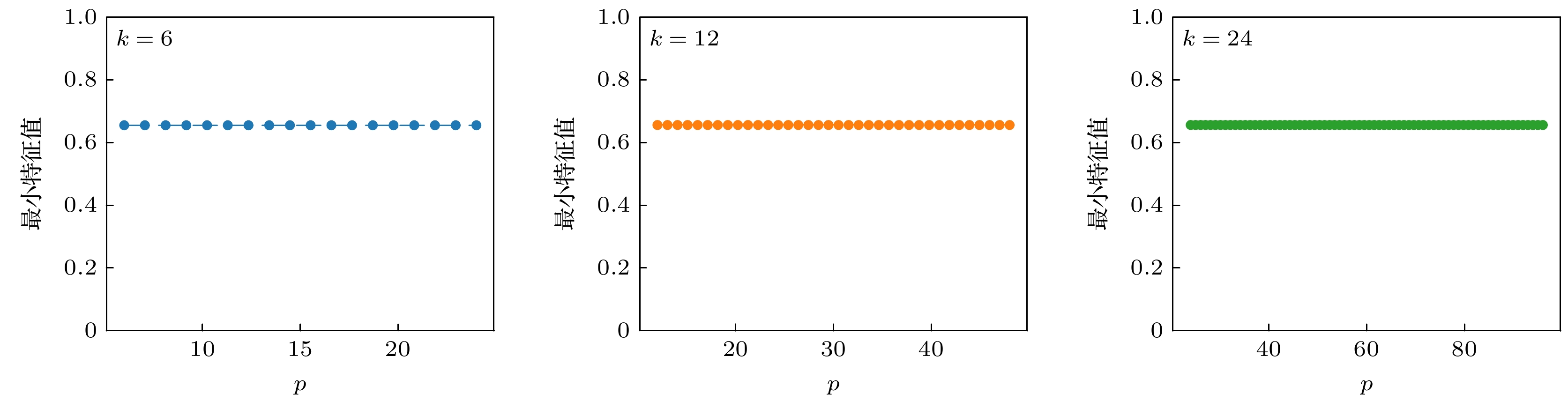
图 5 在E-mail网络中, 分别取$k = 6, 12, 24$, $6 \leqslant p \leqslant 24$, $12 \leqslant p \leqslant 48$, $24 \leqslant p \leqslant 96$($p \in \mathbb{Z}$), $s = 3$时, 最终得到的最小特征值$ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $
Fig. 5. In the E-mail network, when taking respectively $k = 6, 12, 24$ and $6 \leqslant p \leqslant 24$, $12 \leqslant p \leqslant 48$, $24 \leqslant p \leqslant 96$($p \in \mathbb{Z}$), $s = 3$, the final minimum eigenvalue $ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $.
图 6 在NW网络(N = 1000, Nei = 4, pc = 0.1)中, 分别取$k = 6, 12, 24$, $6 \leqslant p \leqslant 24$, $12 \leqslant p \leqslant 48$, $24 \leqslant p \leqslant 96$($p \in \mathbb{Z}$), $s = 3$时, 最终得到的最小特征值$ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $
Fig. 6. In the NW network (N = 1000, Nei = 4, pc = 0.1), when taking respectively $k = 6, 12, 24$ and $6 \leqslant p \leqslant 24$, $12 \leqslant p \leqslant 48$, $24 \leqslant p \leqslant 96$($p \in \mathbb{Z}$), $s = 3$, the final minimum eigenvalue $ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $.
图 7 在E-mail网络中, 分别取$k = 6, 12, 24$, $p = 9, 15, 30$, 当$1 \leqslant s \leqslant 3(s \in \mathbb{Z})$, $1 \leqslant s \leqslant 6(s \in \mathbb{Z})$, $1 \leqslant s \leqslant 12(s \in \mathbb{Z})$时, 最终得到的最小特征值$ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $
Fig. 7. In the E-mail network, when taking respectively $k = 6, 12, 24$, $p = 9, 15, 30$ and $1 \leqslant s \leqslant 3(s \in \mathbb{Z})$, $1 \leqslant s \leqslant 6(s \in \mathbb{Z})$, $1 \leqslant s \leqslant 12(s \in \mathbb{Z})$, the final minimum eigenvalue $ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $.
图 8 生成的NW小世界网络(N = 1000, Nei = 4, pc = 0.1), 标度尺反映了节点度大小的情况
Fig. 8. Generated NW small world network (N = 1000, Nei = 4, pc = 0.1), the scale reflects the magnitude of node degrees.
图 9 NW网络中不同算法去除节点后不同受控节点组规模下最小特征值的比较
Fig. 9. Comparison of minimum eigenvalue with different target node counts following node removal by different algorithms in NW network.
图 10 小世界网络模型中感染数随时间的变化
Fig. 10. Changes in the number of infections over time in the NW network model.
图 11 生成的真实社交网络lastfm_asia (N = 7642), 标度尺反映了节点度大小的情况
Fig. 11. Generated real social network lastfm_asia (N = 7642), the scale reflects the magnitude of node degrees.
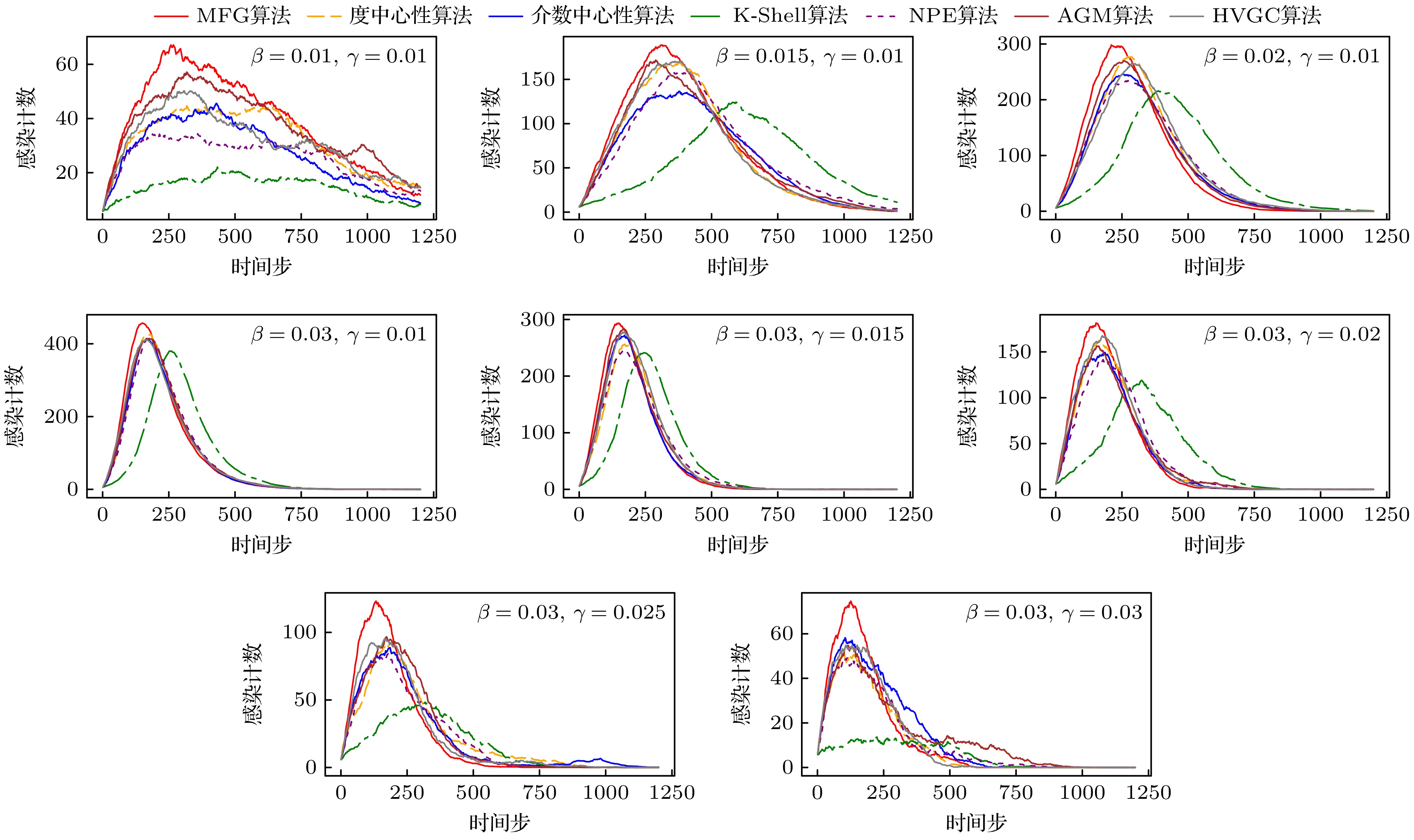
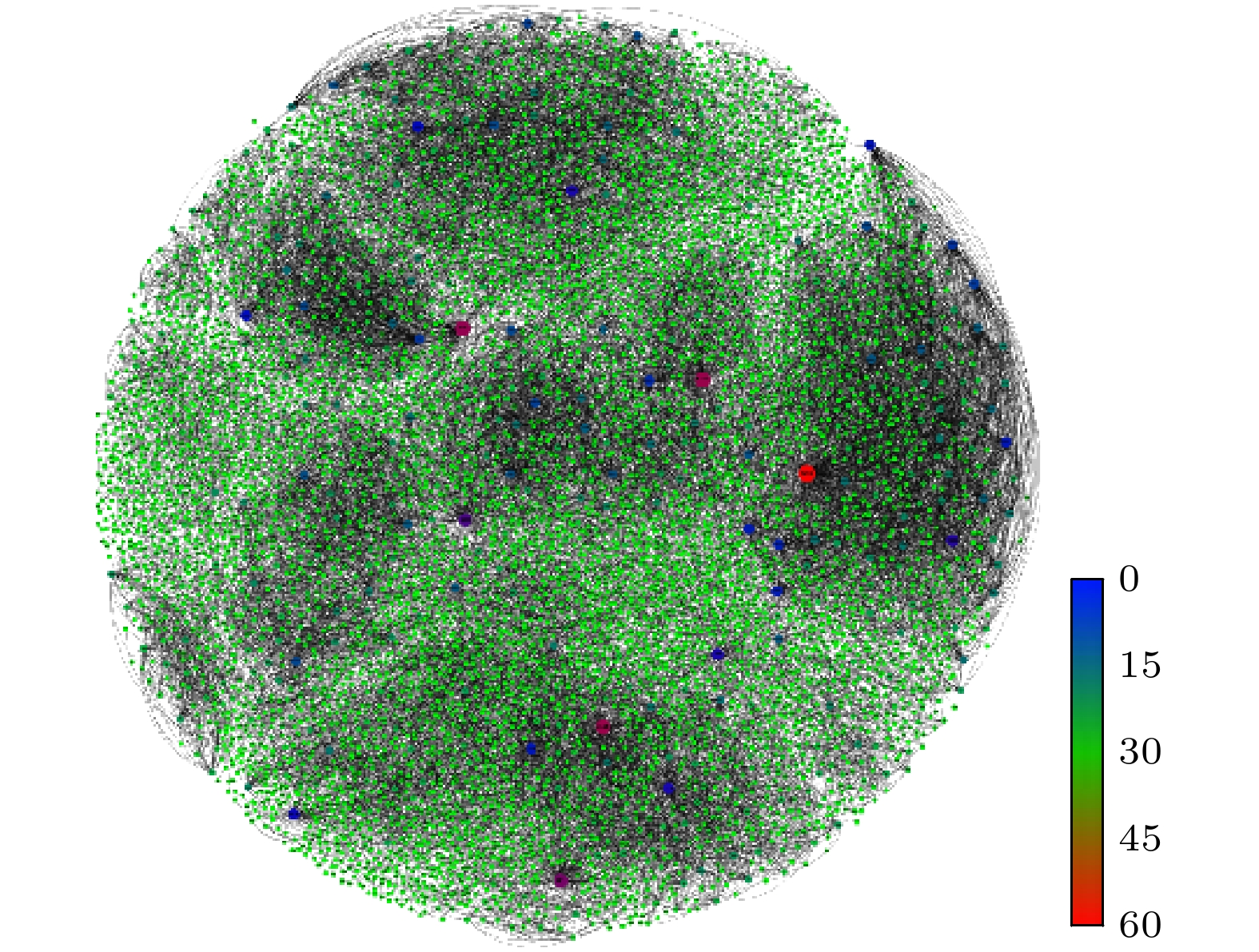
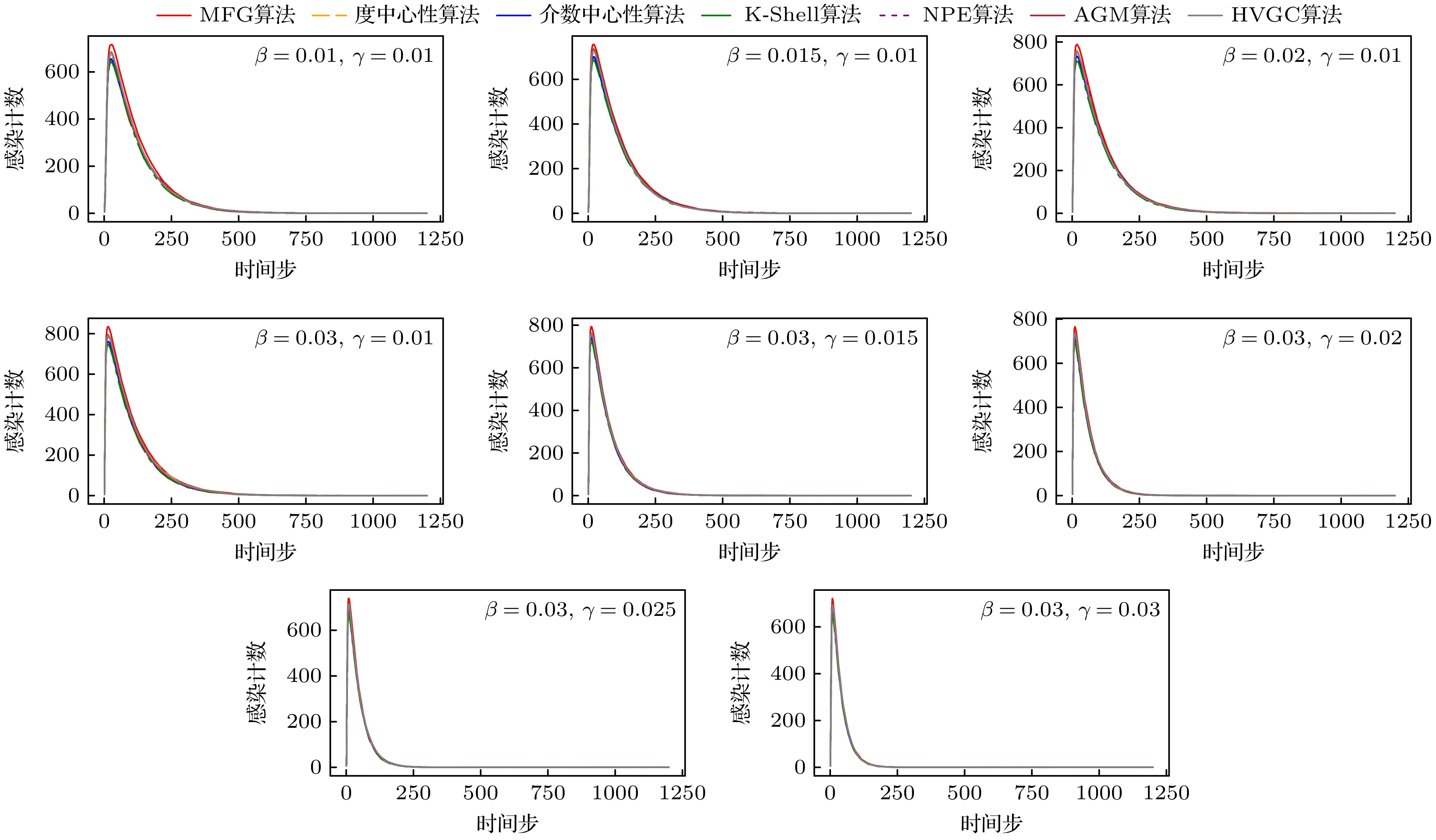
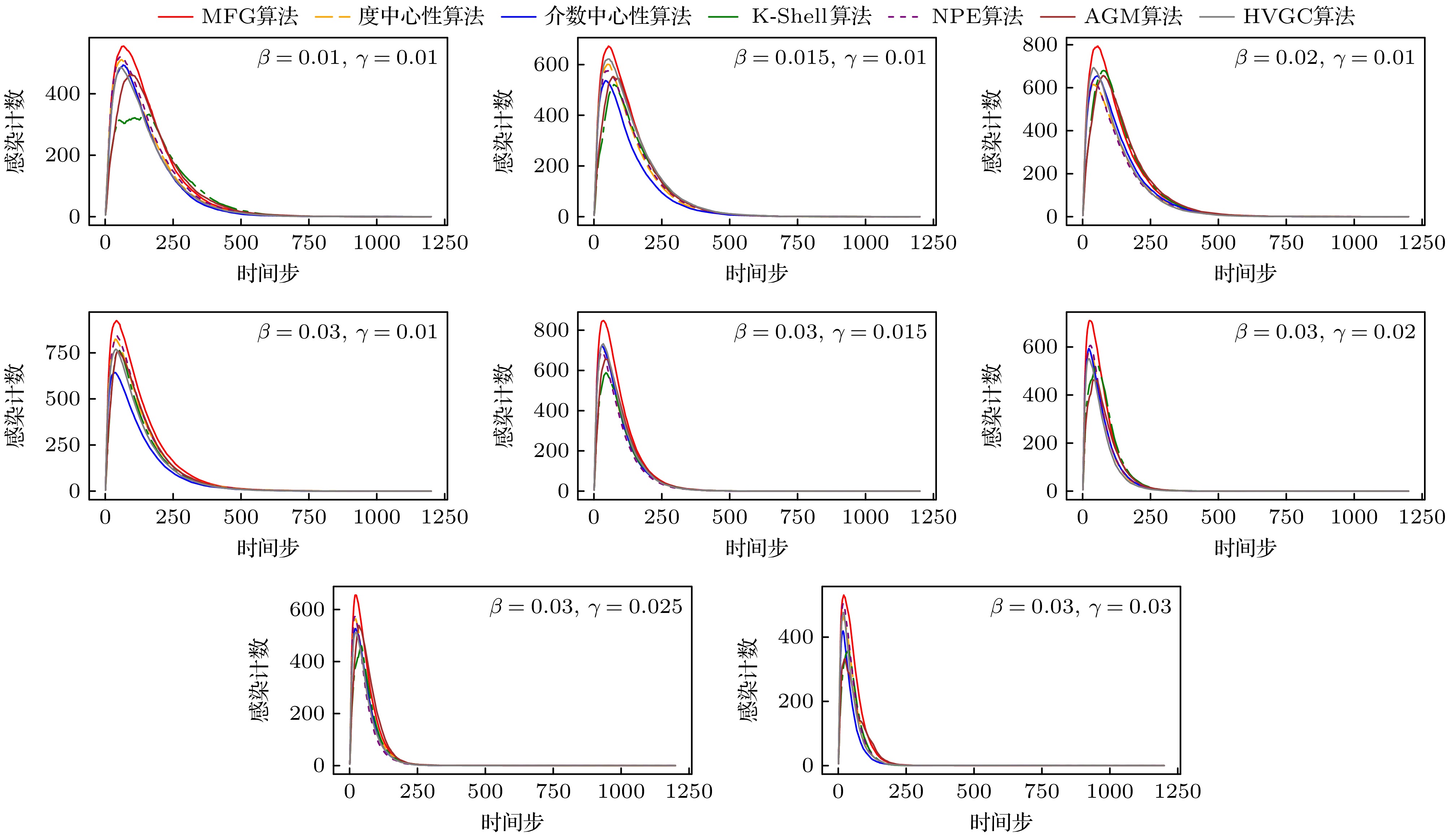
图 12 lastfm_asia网络中不同算法去除节点后不同受控节点组规模下最小特征值$ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $的比较
Fig. 12. Comparison of minimum eigenvalue $ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $ with different target node counts following node removal by different algorithms in lastfm asia network.
图 13 生成的真实社交网络E-mail (N = 1005), 标度尺反映了节点度大小的情况
Fig. 13. Generated real social network E-mail (N = 1005), the scale reflects the magnitude of node degrees.
图 14 E-mail网络中不同算法去除节点后不同受控节点组规模下最小特征值$ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $的比较
Fig. 14. Comparison of minimum eigenvalue $ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $ with different target node counts following node removal by different algorithms in E-mail network.
图 15 E-mail网络感染人数随时间的变化
Fig. 15. Change in the number of infections over time steps in E-mail network.
图 16 Facebook combine网络(N = 1519)
Fig. 16. Structure of the facebook combine Network (N = 1519).
图 17 facebook_combine网络模型(N = 1519)中感染数随时间的变化
Fig. 17. Variation of the number of infections over time in the facebook_combine network model (N = 1519).
表 1 与QR算法相比, 反幂法在乘法次数上的减少情况
Table 1. In comparison to the QR algorithm, the inverse power method exhibits a reduction in the number of multiplications.
N p 乘法次数减少
1004 4.280556 × 108 8 8.56112 × 108 12 1.28417 × 109
10004 7.31605 × 1011 8 1.46321 × 1012 12 2.19481 × 1012
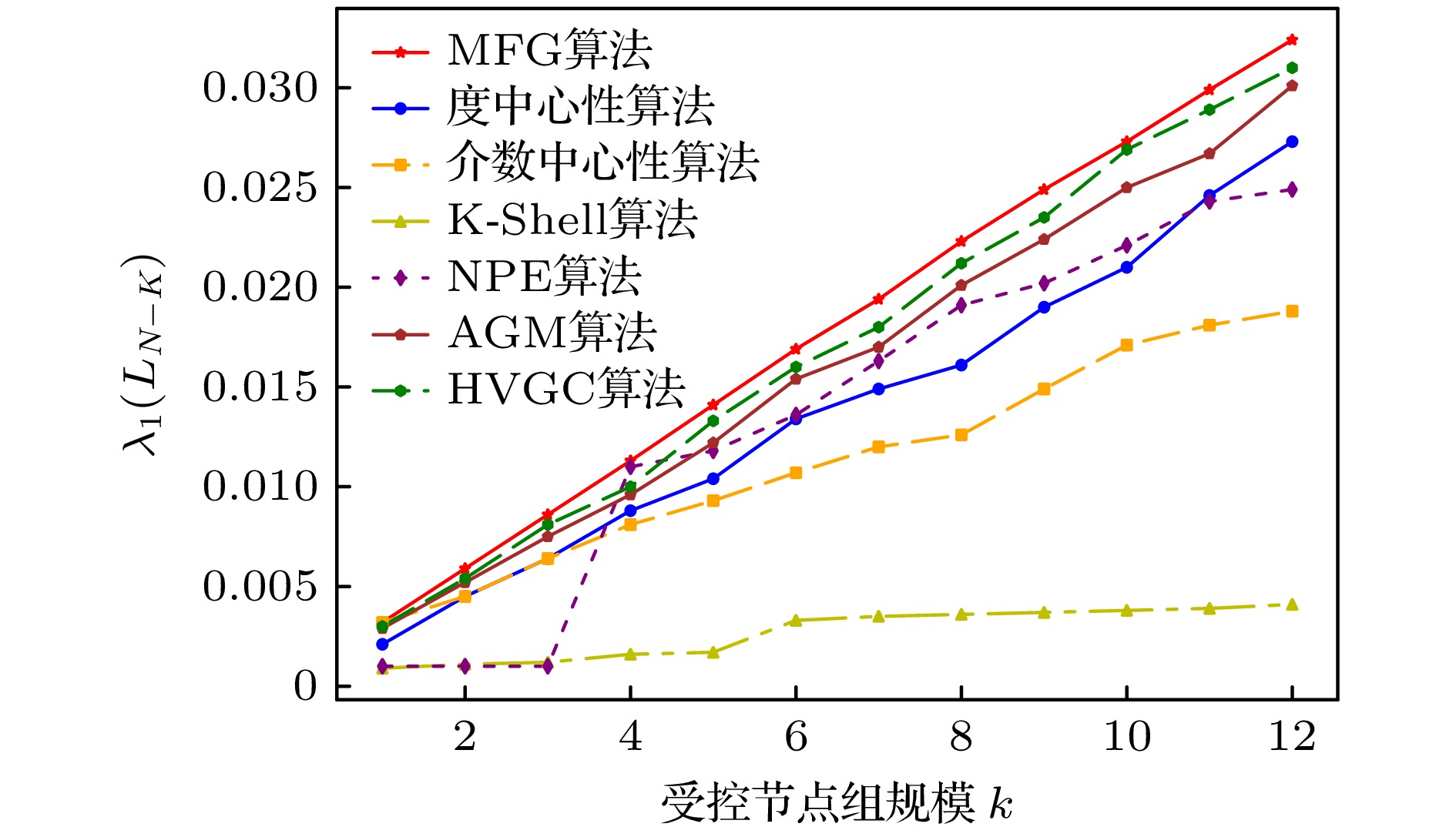
100004 3.73196 × 1015 8 7.46392 × 1016 12 1.11959 × 1017 
下载: 导出CSV
表 2 不同算法在小世界网络中$ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $的对比
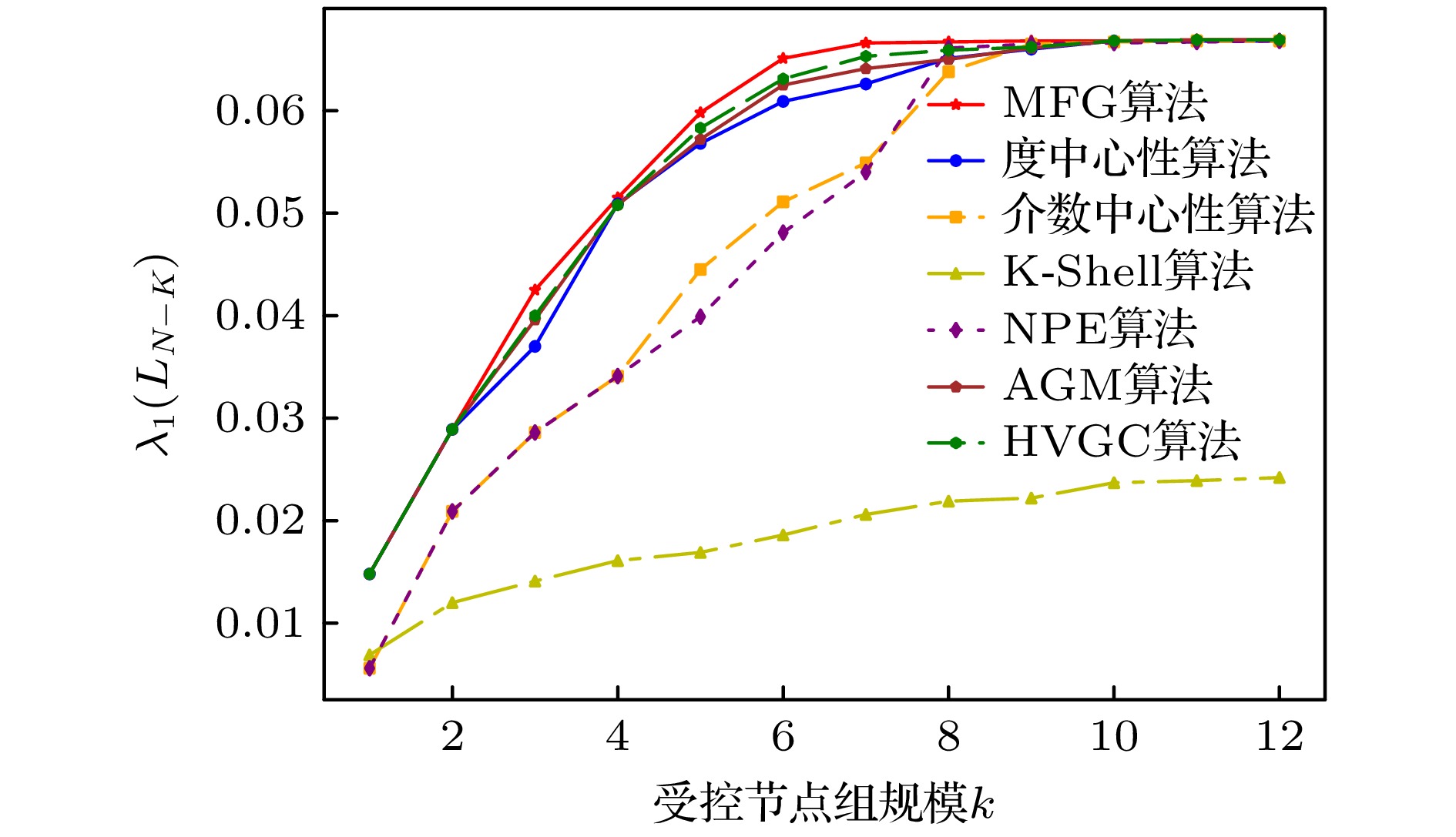
Table 2. Comparison of $ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $ in the NW network for different algorithms.
受控节点组规模k 度中心性算法 介数中心性算法 K-Shell算法 NPE算法 AGM算法 HVGC算法 MFG算法 1 0.0021 0.0032 0.0009 0.0010 0.0029 0.0030 0.0032 2 0.0045 0.0045 0.0011 0.0010 0.0052 0.0054 0.0059 3 0.0064 0.0064 0.0012 0.0010 0.0075 0.0081 0.0086 4 0.0088 0.0081 0.0016 0.0110 0.0096 0.0100 0.0113 5 0.0104 0.0093 0.0017 0.0118 0.0122 0.0133 0.0141 6 0.0134 0.0107 0.0033 0.0136 0.0154 0.0160 0.0169 7 0.0149 0.0120 0.0035 0.0163 0.0170 0.0180 0.0194 8 0.0161 0.0126 0.0036 0.0191 0.0201 0.0212 0.0223 9 0.0190 0.0149 0.0037 0.0202 0.0224 0.0235 0.0249 10 0.0210 0.0171 0.0038 0.0221 0.0250 0.0269 0.0273 11 0.0246 0.0181 0.0039 0.0243 0.0267 0.0289 0.0299 12 0.0273 0.0188 0.0041 0.0249 0.0301 0.0310 0.0324
下载: 导出CSV
表 3 小世界网络不同算法挖掘所得的节点重要性排序
Table 3. Node importance ranking by the different algorithms in NW network.
度中心
性算法介数中心
性算法K-Shell
算法NPE
算法AGM
算法HVGC
算法MFG
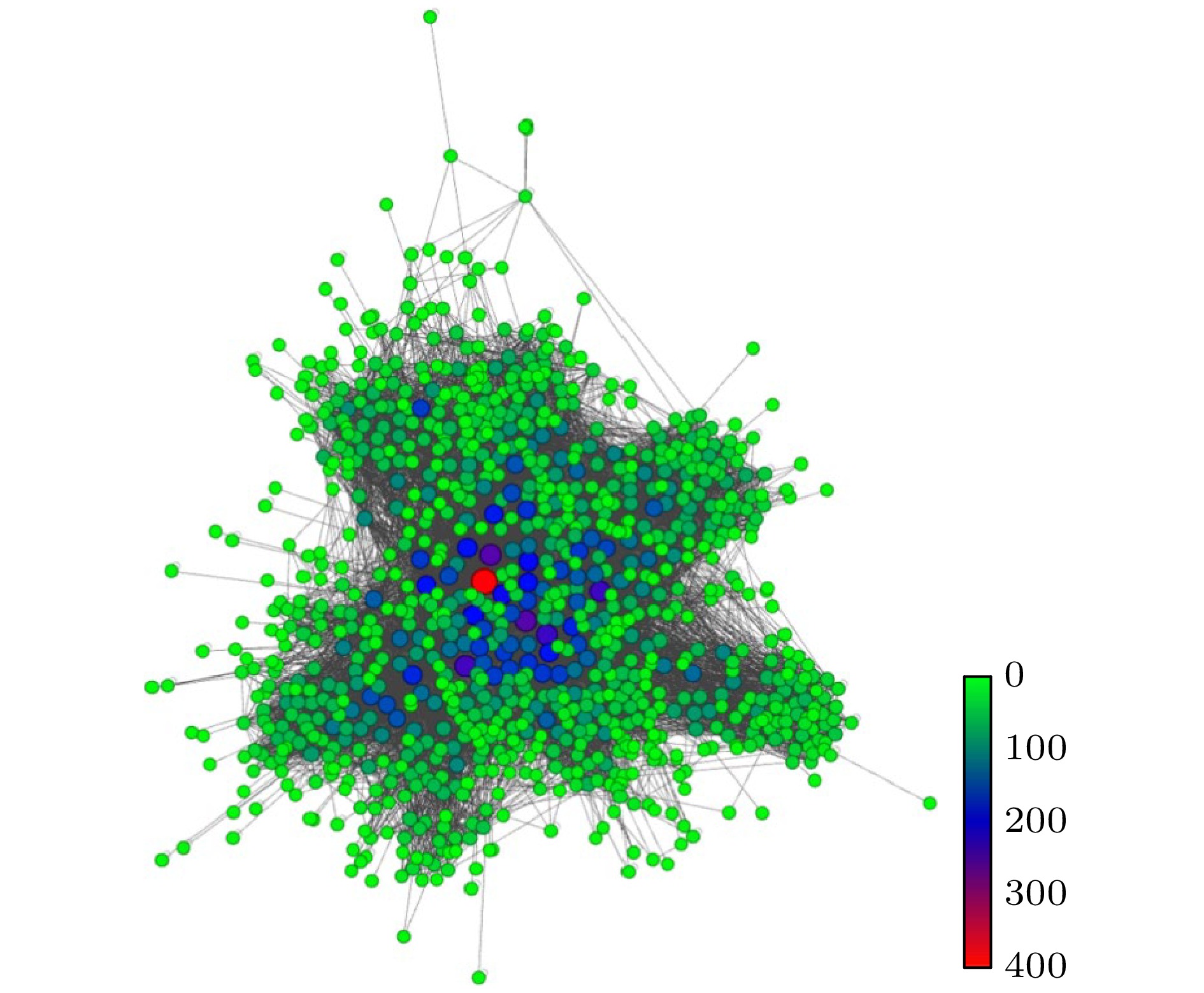
算法4 616 838 616 616 616 616 121 924 839 329 207 523 523 198 329 837 595 523 207 207 236 207 840 207 371 595 236 329 595 238 924 236 924 371 363 236 239 145 887 307 595 371 382 868 307 417 417 417 417 145 869 523 329 329 329 523 307 237 339 339 701 887 560 146 240 676 409 887 701 612 814 836 409 382 382 382 616 915 841 614 937 937 937
下载: 导出CSV
表 4 不同算法在lastfm_asia网络中的$ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $对比
Table 4. Comparison of $ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $ in lastfm_asia network for different algorithms.
受控节点组规模k 度中心性算法 介数中心性算法 K-Shell算法 NPE算法 AGM算法 HVGC MFG算法 1 0.0148 0.0056 0.0069 0.0056 0.0148 0.0148 0.0148 2 0.0289 0.0209 0.0120 0.0209 0.0289 0.0289 0.0289 3 0.0370 0.0286 0.0141 0.0286 0.0396 0.0400 0.0425 4 0.0509 0.0341 0.0161 0.0341 0.0508 0.0508 0.0515 5 0.0568 0.0445 0.0169 0.0399 0.0572 0.0583 0.0598 6 0.0609 0.0511 0.0186 0.0481 0.0625 0.0631 0.0651 7 0.0626 0.0549 0.0206 0.0540 0.0641 0.0653 0.0666 8 0.0651 0.0638 0.0219 0.0661 0.0650 0.0659 0.0667 9 0.0660 0.0665 0.0222 0.0665 0.0661 0.0662 0.0668 10 0.0668 0.0667 0.0237 0.0666 0.0668 0.0668 0.0668 11 0.0668 0.0668 0.0239 0.0667 0.0669 0.0669 0.0669 12 0.0668 0.0668 0.0242 0.0668 0.0669 0.0669 0.0669
下载: 导出CSV
表 5 lastfm_asia网络不同算法挖掘所得的节点重要性排序
Table 5. The node importance ranking by the different algorithms in lastfm_asia network.
度中心
性算法介数中心
性算法K-Shell
算法NPE
算法AGM
算法HVGC
算法MFG
算法7238 7200 379 7200 7238 7238 7238 3531 7238 764 7238 6102 7200 3531 4786 2855 952 2855 3531 6102 6102 525 4357 1335 4357 4786 3531 4786 3451 6102 2453 5455 4357 525 525 2511 5455 3241 5128 3451 2855 1796 3598 4339 3545 3451 1796 5275 3451 2855 5128 3598 6102 5128 3451 5275 5128 3451 4810 3545 4812 4812 4812 6102 4786 4901 4901 5128 4901 2855 4812 3531 5091 4339 525 4357 4357 5579 3104 6109 3531 2855 5128 5128
下载: 导出CSV
表 6 不同算法在Email网络中的$ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $对比
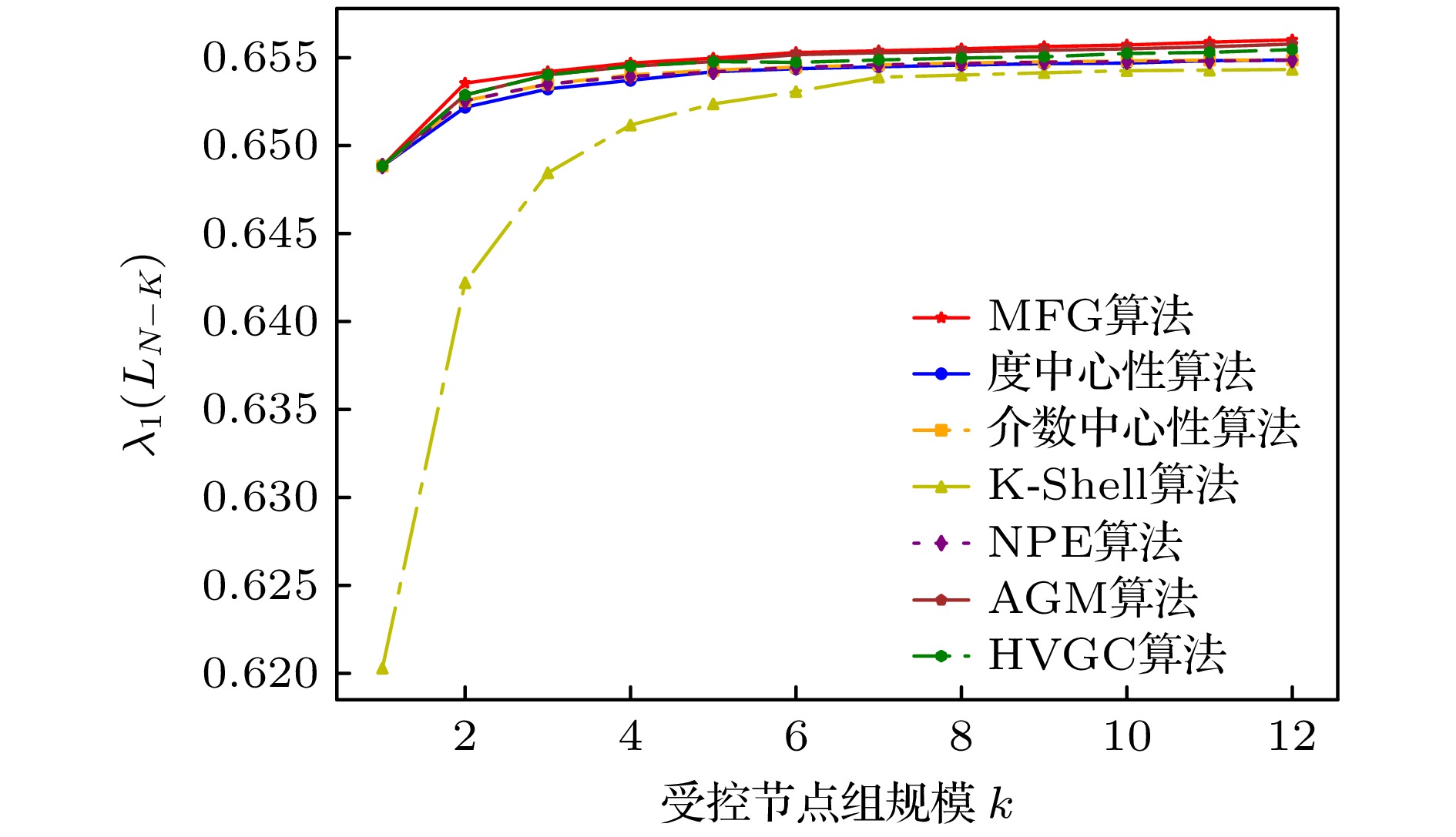
Table 6. Comparison of $ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $ in Email network for different algorithms.
受控节点组规模k 度中心性算法 介数中心性算法 K-Shell算法 NPE算法 AGM算法 HVGC算法 MFG算法 1 0.64884 0.64884 0.62029 0.64884 0.64884 0.64884 0.64884 2 0.65218 0.65255 0.64221 0.65255 0.65288 0.65288 0.65355 3 0.65322 0.65350 0.64845 0.65350 0.65402 0.65402 0.65420 4 0.65371 0.65402 0.65117 0.65393 0.65451 0.65451 0.65469 5 0.65420 0.65429 0.65237 0.65419 0.65478 0.65478 0.65497 6 0.65437 0.65446 0.65307 0.65445 0.65517 0.65473 0.65529 7 0.65448 0.65459 0.65389 0.65459 0.65528 0.65487 0.65539 8 0.65458 0.65470 0.65401 0.65466 0.65534 0.65498 0.65550 9 0.65466 0.65476 0.65414 0.65474 0.65542 0.65505 0.65563 10 0.65469 0.65482 0.65426 0.65477 0.65550 0.65524 0.65572 11 0.65483 0.65486 0.65429 0.65481 0.65562 0.65530 0.65588 12 0.65487 0.65487 0.65433 0.65486 0.65577 0.65546 0.65601
下载: 导出CSV
表 7 E-mail网络不同算法挖掘所得的节点重要性排序
Table 7. The node importance ranking by the different algorithms in E-mail network.
度中心
性算法介数中心
性算法K-Shell
算法NPE
算法AGM
算法HVGC
算法MFG
算法161 161 22 161 161 161 161 122 87 29 122 122 87 87 83 6 82 83 83 83 6 108 83 115 108 108 63 83 87 122 129 63 63 14 122 63 108 130 87 250 6 378 435 14 161 435 435 122 14 14 378 170 250 184 108 108 167 63 213 184 130 65 334 184 65 250 167 167 534 435 6 212 304 130 129 302 63 65 534 372 65 87 167 167
下载: 导出CSV
表 8 不同受控节点组规模下$ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $对比
Table 8. Comparison of $ {\lambda _1}\left( {{{\boldsymbol{L}}_{N - 1}}} \right) $ under different controlled node sizes.
受控节点组规模k 度中心性算法 介数中心性算法 K-Shell算法 NPE算法 AGM算法 HVGC算法 MFG算法 1 0.0137 0.0137 0.0061 0.0056 0.0137 0.0137 0.0137 2 0.1507 0.1507 0.0061 0.0209 0.1507 0.1507 0.1507 3 0.2262 0.2262 0.0061 0.0286 0.2262 0.2262 0.2262 4 0.2263 0.2262 0.0061 0..0341 0.3674 0.5315 0.5789 5 0.2263 0.5789 0.0061 0.0399 0.5899 0.6987 0.7033 6 0.2263 0.7028 0.0061 0.0481 0.7675 0.7543 0.8032 7 0.2263 0.7035 0.0061 0.0540 0.8236 0.9275 1.0000 8 0.2263 0.7288 0.0061 0.0661 1.0000 1.0000 1.0000 9 0.2263 1.0000 0.0061 0.0665 1.0000 1.0000 1.0000 10 0.2263 1.0000 0.0061 0.0666 1.0000 1.0000 1.0000 11 0.2263 1.0000 0.0061 0.0667 1.0000 1.0000 1.0000 12 0.2263 1.0000 0.0062 1.0000 1.0000 1.0000 1.0000
下载: 导出CSV
-
[1] Liu H, Xu X H, Lu J A, Chen G R, Zeng Z G 2021 IEEE Trans. Syst. Man Cybern. Syst. 51 786
Google Scholar
[2] 刘慧, 王炳珺, 陆君安, 李增扬 2021 70 056401
Google Scholar
Liu H, Wang B J, Lu J A, Li Z Y 2021 Acta Phys. Sin. 70 056401
Google Scholar
[3] Zhou F, Su C, Xu S Q, Lü L Y 2022 Chin. Phys. B 31 068901
Google Scholar
[4] Dai J Y, Wang B, Sheng J F, Sun Z J, Khawaja F R, Ullah A 2019 IEEE Access 7 131719
Google Scholar
[5] 孔江涛, 黄健, 龚建兴, 李尔玉 2018 67 098901
Google Scholar
Kong J T, Huang J, Gong J X, Li E Y 2018 Acta Phys. Sin. 67 098901
Google Scholar
[6] 汪亭亭, 梁宗文, 张若曦 2023 72 048901
Google Scholar
Wang T T, Lang Z W, Zhang R X 2023 Acta Phys. Sin. 72 048901
Google Scholar
[7] 杨松青, 蒋沅, 童天驰, 严玉为, 淦各升 2021 70 216401
Google Scholar
Yang S Q, Jiang Y, Tong T C, Yan Y W, Gan G S 2021 Acta Phys. Sin. 70 216401
Google Scholar
[8] 姜廷帅, 阮逸润, 李海, 白亮, 袁逸飞, 于天元 2025 74 126401
Google Scholar
Jiang T S, Ruan Y R, Li H, Bai L, Yuan Y F, Yu T Y 2025 Acta Phys. Sin. 74 126401
Google Scholar
[9] Rezaei A A, Munoz J, Jalili M, Khayyam H 2023 Expert Syst. Appl. 214 119086
Google Scholar
[10] Zhang Y H, Lu Y L, Yang G Z, Hang Z J 2022 Appl. Sci. 12 1944
Google Scholar
[11] 王博雅, 杨小春, 卢升荣, 唐勇平, 洪树权, 蒋惠园 2024 73 226401
Google Scholar
Wang B Y, Yang X C, Lu S R, Tang Y P, Hong S Q, Jiang H Y 2024 Acta Phys. Sin. 73 226401
Google Scholar
[12] Lü L Y, Zhou T, Zhang Q M, Stanley H E 2016 Nat. Commun. 7 10168
Google Scholar
[13] Kou J H, Jia P, Liu J Y, Dai J Q, Luo H R 2023 Neurocomputing 530 23
Google Scholar
[14] Qiu Z H, Fan T L, Li M, Lü L Y 2021 New J. Phys. 23 033036
Google Scholar
[15] Chakrabarti S, Dom B, Raghavan P, Rajagopalan S, Gibson D, Kleinberg J 1998 CNIS 30 65
Google Scholar
[16] Fan C J, Zeng L, Sun Y Z, Liu Y Y 2020 Nat. Mach. Intell. 2 317
Google Scholar
[17] Zhao X Y, Huang B, Tang M, Zhang H F, Chen D B 2014 Europhys. Lett. 108 68005
Google Scholar
[18] Bao Z K, Liu J G, Zhang H F 2017 Phys. Lett. A 381 976
Google Scholar
[19] Ji S G, Lü L Y, Yeung C H, Hu Y Q 2017 New J. Phys. 19 073020
Google Scholar
[20] Anderson R M, May R M 1991 Infectious Diseases of Humans: Dynamics and Control (Oxford University Press
[21] Pastor-Satorras R, Castellano C, Mieghem P V, Vespignani A 2015 Rev. Mod. Phys. 87 925
Google Scholar
[22] Feng M L, Zhang S F, Xia C Y, Zhao D W 2024 Chaos 34 073128
Google Scholar
[23] Avraam D, Hadjichrysanthou C 2024 J. Theor. Biol. 599 112010
Google Scholar
[24] Lu J A, Liu H, Chen J 2016 Synchronization in Complex Dynamical Networks (Vol. 1) (Beijing: Higher Education Press) p49
[25] Pirani M, Sundaram S 2016 IEEE Trans. Autom. Control 61 509
Google Scholar
[26] Bapat R B 2010 Graphs and Matrices (Springer London
[27] Zhu H Y, Klein D J, Lukovits I 1996 J. Chem. Inf. Model. 36 420
Google Scholar
[28] Gutman I, Mohar B 1996 J. Chem. Inf. Comput. Sci. 36 982
Google Scholar
[29] 关治, 陈景良 1990 数值计算方法(北京: 清华大学出版社)
Guan Z, Chen J L 1990 Numerical Calculation Method (Beijing: Tsinghua University Press
[30] 刘砚青, 陆君安 2007 复杂系统与复杂性科学 4 13
Liu Y Q, Lu J A 2007 Complex Syst. Complexity Sci. 4 13
[31] Dean J, Ghemawat S 2008 Commun. ACM 51 107
Google Scholar
[32] Yin H, Benson A R, Leskovec J, Gleich D F 2017 Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’17 ) Halifax, NS, Canada, August 13–17, 2017 p555
[33] 吴英晗, 田阔, 李明达, 胡枫 2023 计算机工程与应用 19 66
Google Scholar
Wu Y H, Tian K, Li M D, Hu F 2023 Comput. Appl. Eng. Educ. 19 66
Google Scholar
[34] Meng L, Xu G Q, Dong C 2025 Physica A 657 130237
Google Scholar
[35] Zhu S Q, Zhan J, Li X 2023 Sci. Rep. 13 16404
Google Scholar
[36] Snap: Stanford network analysis project https://snap.stanford.edu/.
[37] Jiang W C, Wang Y H 2020 IEEE Access 8 32432
Google Scholar
下载:
计量
- 文章访问数: 610
- PDF下载量: 15
- 被引次数: 0
