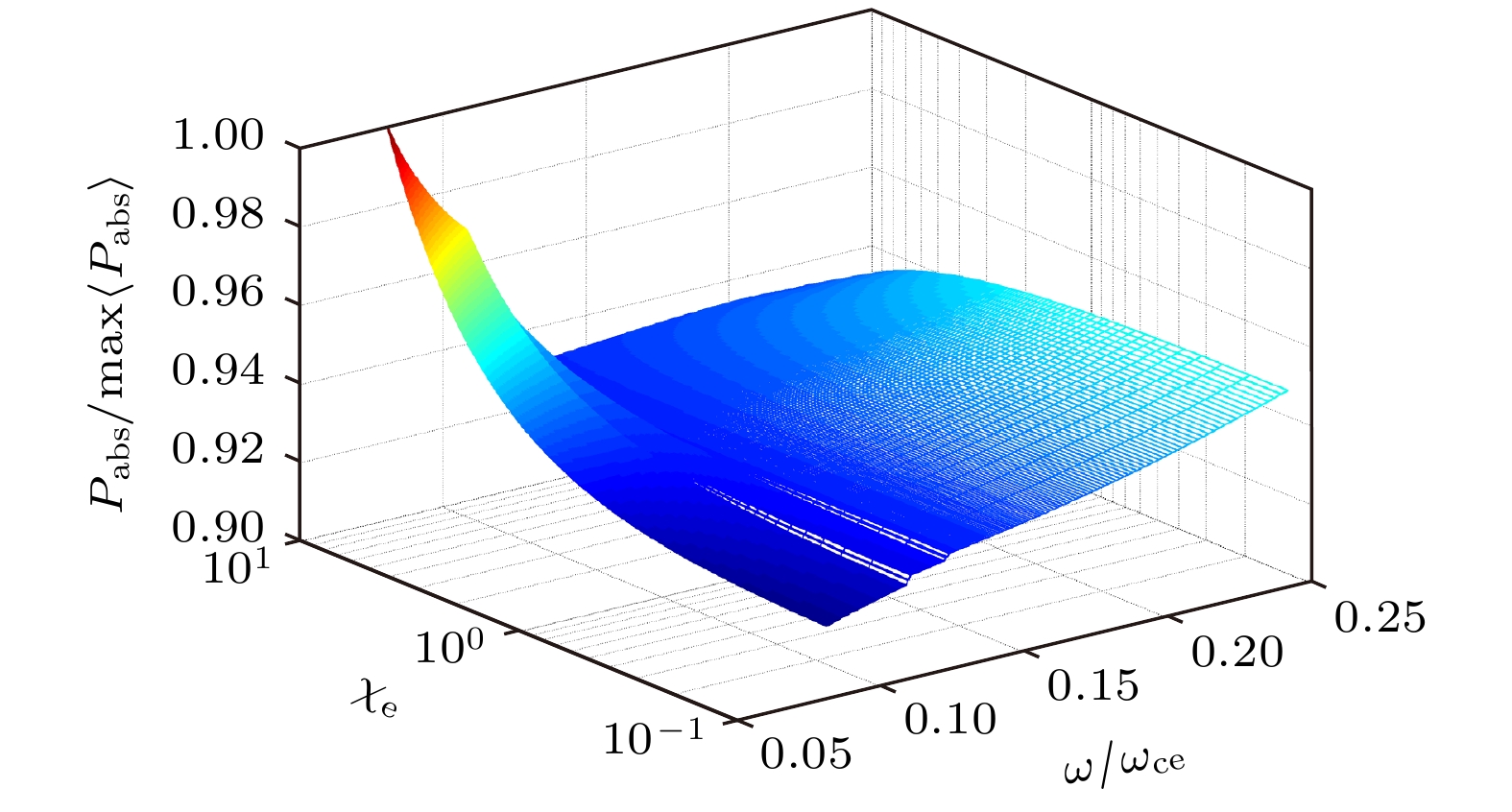
-
深入理解螺旋波等离子体中的低磁场密度峰值现象, 对全面揭示螺旋波放电机制至关重要. 本研究基于低温等离子体动理学效应和带电粒子温度各向异性假设, 利用均匀等离子体中电磁波的一般色散关系, 理论分析了低磁场(<100 G (1 G = 10–4 T))、低气压条件下Trivelpiece-Gould (TG) 波的色散特性、波数关系及功率沉积特性. 研究结果表明: 在波频率ω/2π = 13.56 MHz、离子与电子轴向温度比值Ti, z/Te, z = 0.1、等离子体密度n0 = 1×1011 cm–3、中性气体(Ar)气压pAr = 0.5 mTorr (1 mTorr = 0.133 Pa)参量条件下, 粒子间的碰撞阻尼效应彻底改变了螺旋波与TG波的色散特性和波数关系; 对于TG波 m = 0角向模, n = 1径向模较其余高次径向模在功率沉积中扮演主要角色; 对于TG波(m = 0, n = 1)模, 在电子温度Te, z $\in $ (3, 8) eV范围内, 在低磁场和电子温度各向异性因子$\chi_{\rm{e}} \ll 1 $(χe = Te, ⊥/Te, z)条件下朗道阻尼在功率沉积中占据主导地位, 而在高磁场和$ \chi_{\rm{e}} \gg 1$条件下碰撞阻尼主导功率沉积.
Low-field peak phenomenon, which has been observed in low magnetic helicon plasma discharge, is generally considered to have great commercial value in the field of low-cost semiconductor etching ion sources. As an important phenomenon in helicon plasma discharge, in-depth theoretical investigation on it may help us fully understand the physical mechanism behind the helicon plasma discharge. As a theoretical attempt to explore this phenomenon, which still lacks a unified explanation, we employ a plasma dielectric tensor model that better aligns with the actual discharge situation. Specifically, we use the general plasma dielectric tensor while accounting for the low temperature plasma kinetic effects and charged particle temperature anisotropy. Under typical helicon plasma discharge parameters, i.e. wave frequency ω/2π = 13.56 MHz, plasma column radius a = 3 cm, neutral gas pressure pAr = 0.5 mTorr, plasma density n0 = 1 × 1011 cm–3, and ratio of axial ion temperature to axial electron temperature Ti, z/Te, z = 0.1, we theoretically investigate the dispersion characteristics and wave number relations of Whistler waves, the mode coupling between helicon and Trivelpiece-Gould (TG) waves, and the power deposition properties of TG wave in low magnetic field circumstances. Analytical results suggest that under low electron temperature Te = 3 eV and low magnetic field (B0 < 48 G) circumstances, the high-order (|s| > 1) electron cyclotron harmonics can be ignored; the electron finite Larmor radius effect should be considered, while the ion finite Larmor radius effect can be ignored; the collision effect (collision damping) among particles completely changes the dispersion characteristics and wave number relations of the Whistler waves; for the helicon and TG waves, the value B0, mcs (where the mode coupling surface (MCS) is located) decreases with the increase of the axial wave number, meanwhile, the collision effect greatly affects the mode coupling characteristic of helicon and TG waves near the mode coupling surface; collision damping and Landau damping respectively dominate wave power deposition in different axial electron temperature ranges; in the typical helicon plasma electron temperature range, Te, z ∈ (3, 8) eV, the TG wave (m = 0, n = 1) mode dominates the power deposition; for the TG wave (m = 0, n = 1) mode, its power deposition peaks at the central axis of the plasma column, for low perpendicular electron temperature and low magnetic field, Landau damping dominates the power deposition, while under high perpendicular electron temperature and higher magnetic field, the collision damping dominates the power deposition. These conclusions not only further deepens our understanding of the low magnetic field density peak phenomenon at the theoretical level, but also provides new clues for fully revealing the mechanism of helicon discharge mechanism. -
Keywords:
- plasma kinetic equations /
- electromagnetic waves /
- dispersion characteristics /
- nonlinear phenomena
[1] Degeling A W, Jung C O, Boswell R W, Ellingboe A R 1996 Phys. Plasmas 3 2788
Google Scholar
[2] Chen F F, Jiang X, Evans J D, Tynan G, Arnush D 1997 Plasma Phys. Controlled Fusion 39 A411
Google Scholar
[3] Braginskii O V, Vasil'Eva A N, Kovalev A S 1998 Plasma Phys. Rep. 24 762
Google Scholar
[4] Wang S J, Kwak J G, Kim C B, Kim S K 2003 Phys. Lett. A 313 278
Google Scholar
[5] Shinohara S, Soejima T 1998 Plasma Phys. Controlled Fusion 40 2081
Google Scholar
[6] Degeling A W, Borg G G, Boswell R W 2004 Phys. Plasmas 11 2144
Google Scholar
[7] Lafleur T, Charles C, Boswell R W 2010 Phys. Plasmas 17 073508
Google Scholar
[8] Chen F F 1992 J. Vac. Sci. Technol. , A 10 1389
Google Scholar
[9] Chen F F 2003 Phys. Plasmas 10 2586
Google Scholar
[10] Cho S 2006 Phys. Plasmas 13 033504
Google Scholar
[11] Sato G, Oohara W, Hatakeyama R 2007 Plasma Sources Sci. Technol. 16 734
Google Scholar
[12] Barada K K, Chattopadhyay P K, Ghosh J, Kumar S, Saxena Y C 2013 Phys. Plasmas 20 042119
Google Scholar
[13] Wang Y, Zhao G, Liu Z W, Ouyang J T, Chen Q 2015 Phys. Plasmas 22 093507
Google Scholar
[14] Cui R, Zhang T, He F, Zheng B, Ouyang J 2024 Plasma Sources Sci. Technol. 33 025021
Google Scholar
[15] Swanson D G 1989 Plasma Waves (New York: Academic Press) p155
[16] 李文秋, 唐彦娜, 刘雅琳, 王刚 2024 73 075202
Google Scholar
Li W Q, Tang Y N, Liu Y L, Wang G 2024 Acta Phys. Sin. 73 075202
Google Scholar
[17] Fried B D, Conte S D 2015 The Plasma Dispersion Function: the Hilbert Transform of the Gaussian (New York: Academic Press) p1
[18] Huba J D 2016 NRL Plasma Formulary (Washington: Naval Research Laboratory) p34
[19] Kamenski I V, Borg G G 1998 Comput. Phys. Commun. 113 10
Google Scholar
[20] 李文秋, 唐彦娜, 刘雅琳, 王刚 2023 72 055202
Google Scholar
Li W Q, Tang Y N, Liu Y L, Wang G 2023 Acta Phys. Sin. 72 055202
Google Scholar
[21] Mouzouris Y, Scharer J E 1998 Phys. Plasmas 5 4253
Google Scholar
[22] Martin P, Olivares J, Maass F, Valero E 2018 Results Phys. 11 1028
Google Scholar
[23] Chen F F, Arnush D 1997 Phys. Plasmas 4 3411
Google Scholar
[24] Borg G, Boswell R 1998 Phys. Plasmas 5 564
Google Scholar
[25] Glaude V M M, Moisan M, Pantel R, Leprince P, Marec J 1980 J. Appl. Phys. 51 5693
Google Scholar
[26] Shamrai K P, Shinohara S 2001 Phys. Plasmas 8 4659
Google Scholar
[27] 李文秋, 赵斌, 王刚, 相东 2020 69 115201
Google Scholar
Li W Q, Zhao B, Wang G, Xiang D 2020 Acta Phys. Sin. 69 115201
Google Scholar
[28] Loewenhardt P K, Blackwell B D, Boswell R W, Conway G D, Hamberger S M 1991 Phys. Rev. Lett. 67 2792
Google Scholar
-
图 2 等离子体色散函数宗量随归一化电子回旋频率的对应关系
Fig. 2. Relation of the plasma dispersion function argument on normalized electron cyclotron frequency.
图 3 有限拉莫尔半径效应因子随归一化电子回旋频率的变化
Fig. 3. Dependence of the finite Larmor radius effects on normalized electron cyclotron frequency.
图 4 Whistler波的色散关系(ω - kz 空间) (a) 碰撞频率$ {\nu _\ell } = 0 $; (b) 碰撞频率$ {\nu _\ell } \ne 0 $
Fig. 4. Dispersion relation of Whistler waves (ω - kz space): (a) collisional frequency $ {\nu _\ell } = 0 $; (b) collisional frequency $ {\nu _\ell } \ne 0 $.
图 5 Whistler波的色散关系(k⊥-kz 空间)
Fig. 5. Dispersion relation of the whistler waves (k⊥-kz space)
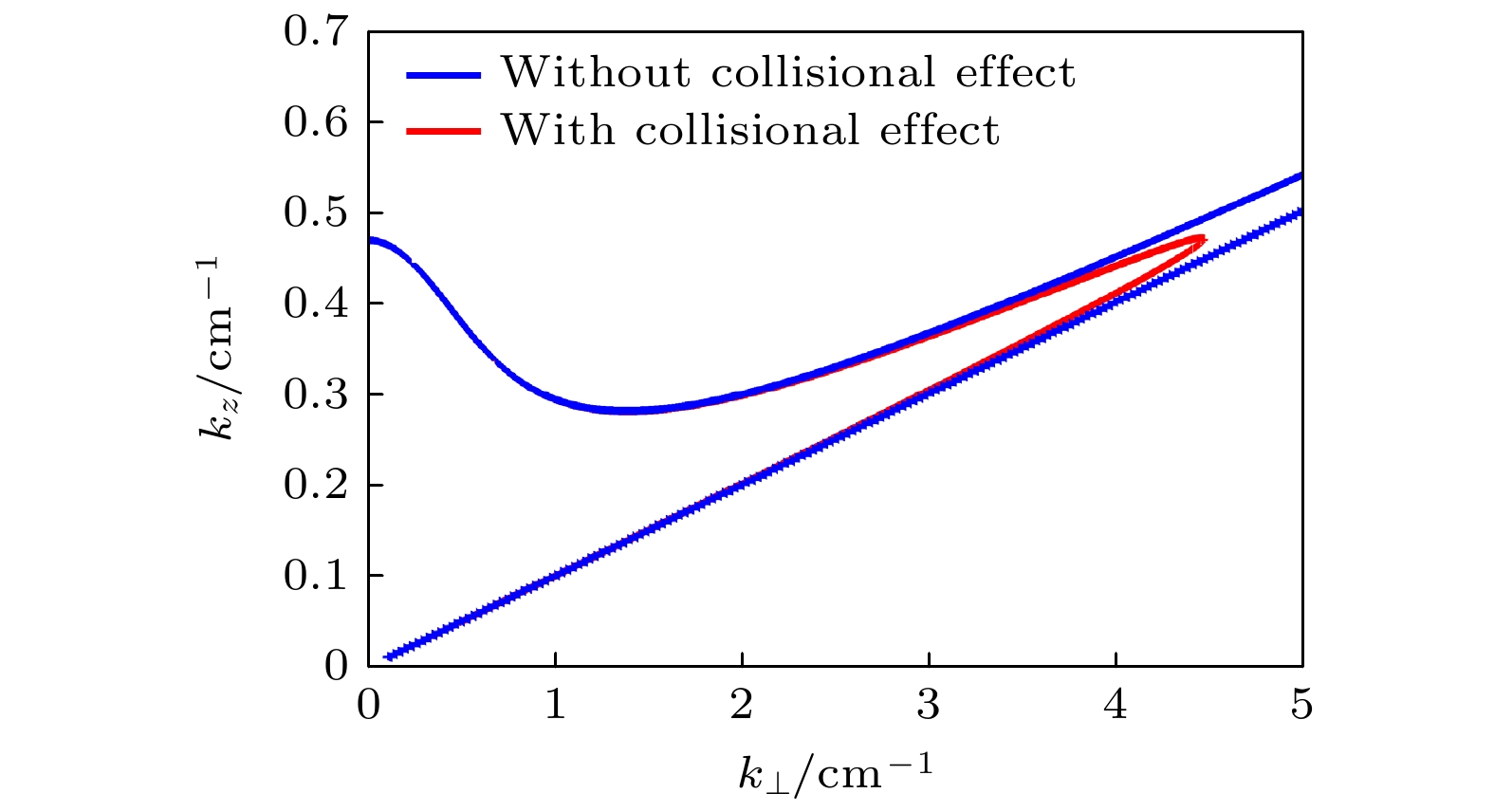
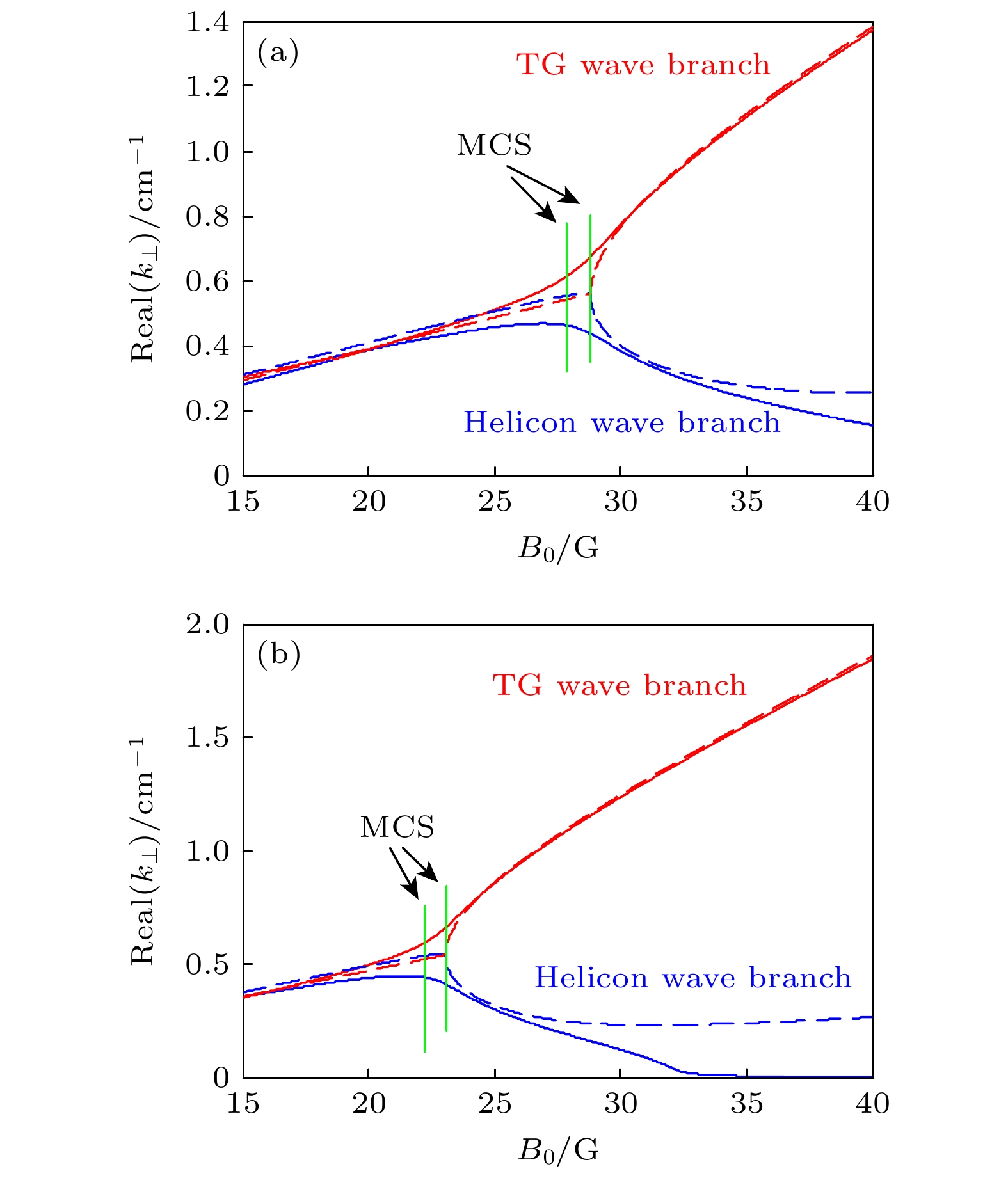
图 6 给定轴向波数时螺旋波与TG波横向波数的实部随轴向静磁场的变化 (a) $ {k_z} = 0.2{\text{ c}}{{\text{m}}^{ - 1}} $; (b)$ {k_z} = 0.25{\text{ c}}{{\text{m}}^{ - 1}} $
Fig. 6. Dependence of real part of the perpendicular wave number of helicon and TG waves on axial static magnetic field for given axial wave number: (a) Axial wave number $ {k_z} = 0.2{\text{ c}}{{\text{m}}^{ - 1}} $; (b) axial wave number $ {k_z} = 0.25{\text{ c}}{{\text{m}}^{ - 1}} $.
图 7 TG波(m = 0, n = 1)模的碰撞阻尼频率和朗道阻尼频率
Fig. 7. Collision damping frequency and Landua damping frequency of the TG wave (m = 0, n = 1) mode.
图 8 TG波$m = 0$角向模对应的前三个径向模的功率沉积比较
Fig. 8. Comparison of power deposition for the first three radial modes of the m = 0 TG wave.
图 9 TG波(m = 0, n = 1)模归一化功率沉积在(r, Te, z)参量空间的分布
Fig. 9. Normalized power deposition of the TG wave (m = 0, n = 1) mode in the (r, Te, z) parameter space.
图 10 TG波(m = 0, n = 1)模归一化功率沉积在(ω/ωce, χe)参量空间的分布
Fig. 10. Normalized power deposition of the TG wave (m = 0, n = 1) mode in the (ω/ωce, χe) parameter space.
-
[1] Degeling A W, Jung C O, Boswell R W, Ellingboe A R 1996 Phys. Plasmas 3 2788
Google Scholar
[2] Chen F F, Jiang X, Evans J D, Tynan G, Arnush D 1997 Plasma Phys. Controlled Fusion 39 A411
Google Scholar
[3] Braginskii O V, Vasil'Eva A N, Kovalev A S 1998 Plasma Phys. Rep. 24 762
Google Scholar
[4] Wang S J, Kwak J G, Kim C B, Kim S K 2003 Phys. Lett. A 313 278
Google Scholar
[5] Shinohara S, Soejima T 1998 Plasma Phys. Controlled Fusion 40 2081
Google Scholar
[6] Degeling A W, Borg G G, Boswell R W 2004 Phys. Plasmas 11 2144
Google Scholar
[7] Lafleur T, Charles C, Boswell R W 2010 Phys. Plasmas 17 073508
Google Scholar
[8] Chen F F 1992 J. Vac. Sci. Technol. , A 10 1389
Google Scholar
[9] Chen F F 2003 Phys. Plasmas 10 2586
Google Scholar
[10] Cho S 2006 Phys. Plasmas 13 033504
Google Scholar
[11] Sato G, Oohara W, Hatakeyama R 2007 Plasma Sources Sci. Technol. 16 734
Google Scholar
[12] Barada K K, Chattopadhyay P K, Ghosh J, Kumar S, Saxena Y C 2013 Phys. Plasmas 20 042119
Google Scholar
[13] Wang Y, Zhao G, Liu Z W, Ouyang J T, Chen Q 2015 Phys. Plasmas 22 093507
Google Scholar
[14] Cui R, Zhang T, He F, Zheng B, Ouyang J 2024 Plasma Sources Sci. Technol. 33 025021
Google Scholar
[15] Swanson D G 1989 Plasma Waves (New York: Academic Press) p155
[16] 李文秋, 唐彦娜, 刘雅琳, 王刚 2024 73 075202
Google Scholar
Li W Q, Tang Y N, Liu Y L, Wang G 2024 Acta Phys. Sin. 73 075202
Google Scholar
[17] Fried B D, Conte S D 2015 The Plasma Dispersion Function: the Hilbert Transform of the Gaussian (New York: Academic Press) p1
[18] Huba J D 2016 NRL Plasma Formulary (Washington: Naval Research Laboratory) p34
[19] Kamenski I V, Borg G G 1998 Comput. Phys. Commun. 113 10
Google Scholar
[20] 李文秋, 唐彦娜, 刘雅琳, 王刚 2023 72 055202
Google Scholar
Li W Q, Tang Y N, Liu Y L, Wang G 2023 Acta Phys. Sin. 72 055202
Google Scholar
[21] Mouzouris Y, Scharer J E 1998 Phys. Plasmas 5 4253
Google Scholar
[22] Martin P, Olivares J, Maass F, Valero E 2018 Results Phys. 11 1028
Google Scholar
[23] Chen F F, Arnush D 1997 Phys. Plasmas 4 3411
Google Scholar
[24] Borg G, Boswell R 1998 Phys. Plasmas 5 564
Google Scholar
[25] Glaude V M M, Moisan M, Pantel R, Leprince P, Marec J 1980 J. Appl. Phys. 51 5693
Google Scholar
[26] Shamrai K P, Shinohara S 2001 Phys. Plasmas 8 4659
Google Scholar
[27] 李文秋, 赵斌, 王刚, 相东 2020 69 115201
Google Scholar
Li W Q, Zhao B, Wang G, Xiang D 2020 Acta Phys. Sin. 69 115201
Google Scholar
[28] Loewenhardt P K, Blackwell B D, Boswell R W, Conway G D, Hamberger S M 1991 Phys. Rev. Lett. 67 2792
Google Scholar
下载:
计量
- 文章访问数: 368
- PDF下载量: 24
- 被引次数: 0
