-
光学非互易性因其能够有效地用于全光二极管、隔离器等新型光子器件的设计, 近年来相关研究备受关注. 本研究组在2024年利用晶格缺陷打破极化率空间对称性实现了非互易光反射, 该工作中缺陷是由固定数量空晶格周期性调制的. 为了进一步展开缺陷原子晶格中非互易光传播特性的研究, 我们提出用斐波那契数列调控空晶格的排布规律, 构成准周期缺陷原子晶格系统, 实现了探测光左右反射非互易的操控. 分析了单个准周期中满晶格数量、斐波那契数列和准周期数对非互易反射的优化过程以及产生影响的物理实质, 并讨论了耦合场失谐对非互易频率域和带宽的调制. 这些结果为宽频、对比度高的非互易光反射调控提供了更多的自由度, 在量子计算和信息处理领域具有潜在的应用.In order to further investigate the non-reciprocity of light propagation in the defective atomic lattices, and due to its effective application in designing novel photonic devices, such as all-optical diodes and isolators, which are powerful tools for information processing and quantum simulation, we innovatively propose to use the Fibonacci sequence to modulate the arrangement of empty lattice cells that form a quasi periodic defective atomic lattices. In the electromagnetically induced transparency window, the probe light is almost not absorbed under the control of a strong coupling field (see Fig. 1). The numerical simulation indicates that a wide nonreciprocal reflection band can be achieved by modulating the number of filled lattice cells, Fibonacci sequence, the period number in a single quasi period (see Fig. 2). These results provide more degrees of freedom for regulating nonreciprocal reflection with wide bandwidth and high contrast, and have potential applications in quantum computing and information processing.
[1] White A D, Ahn G H, Gasse K V, Yang K Y, Chang L, Bowers J E, Vučković J 2023 Nat. Photonics 17 143
Google Scholar
[2] Prabu K, Nasre D 2019 Plasmonics 14 1261
Google Scholar
[3] Xia K Y, Nori F, Xiao M 2018 Phys. Rev. Lett. 121 203602
Google Scholar
[4] Tian H, Liu J Q, Siddharth A, Wang R N, Blésin T, He J J, Kippenberg T J, Bhave S A 2021 Nat. Photonics 15 828
Google Scholar
[5] Chan E H W 2014 Opt. Commun. 324 127
Google Scholar
[6] Litinskaya M, Shapiro E A 2015 Phys. Rev. A 91 033802
Google Scholar
[7] Shen H Z, Wang Q, Wang J, Yi X X 2020 Phys. Rev. A 101 013826
Google Scholar
[8] Wu J, Wang Z M, Zhai H, Shi Z X, Wu X H, Wu F 2021 Opt. Mater. Express 11 4058
Google Scholar
[9] Wang Z Y, Qian J, Wang Y P, Li J, You J Q 2023 Appl. Phys. Lett. 123 153904
Google Scholar
[10] Chakraborty S, Das C 2023 Phys. Rev. A 108 063704
Google Scholar
[11] Wang Y M, Xiong W, Xu Z Y, Zhang G Q, You J Q 2022 Sci. China-Phys. , Mech. Astron. 65 260314
Google Scholar
[12] He X W, Wang Z Y, Han X, Zhang S, Wang H F 2023 Opt. Express 31 43506
Google Scholar
[13] Yang Y, Guan B, Zhang C L, Liu L C, Liu K 2020 Optoelectron. Sci. Mater. 11606 74
[14] Kim M K 2015 Opt. Express 23 2040
Google Scholar
[15] Kawaguchi Y, Alù A, Khanikaev A B 2022 Opt. Mater. Express 12 1453
Google Scholar
[16] Sounas D L, Alù A 2017 Nat. Photonics 11 774
Google Scholar
[17] Fleury R, Sounas D L, Alù A 2018 J. Opt. 20 034007
Google Scholar
[18] Cardin A E, Silva S R, Vardeny S R, Padilla W J, Saxena A, Taylor A J, Kort-Kamp W J M, Chen H T, Dalvit D A R, Azad A K 2020 Nat. Commun. 11 1469
Google Scholar
[19] Kittlaus E A, Otterstrom N T, Kharel P, Gertler S, Rakich P T 2018 Nat. Photonics 12 613
Google Scholar
[20] Sohn D B, Kim S, Bahl G 2018 Nat. Photonics 12 91
Google Scholar
[21] Rodriguez S R K, Goblot V, Zambon N C, Amo A, Bloch J 2019 Phys. Rev. A 99 013851
Google Scholar
[22] Shen Z, Zhang Y L, Chen Y, Zou C L, Xiao Y F, Zou X B, Sun F W, Guo G C, Dong C H 2016 Nat. Photonics 10 657
Google Scholar
[23] Ruesink F, Miri M A, Alù A, Verhagen E 2016 Nat. Commun. 7 13662
Google Scholar
[24] Barzanjeh S, Wulf M, Peruzzo M, Kalaee M, Dieterle P B , Painter O, Fink J M 2017 Nat. Commun. 8 953
Google Scholar
[25] Tang L, Tang J S, Chen M Y, Nori F, Xiao M, Xia K Y 2022 Phys. Rev. Lett. 128 083604
Google Scholar
[26] Yang P F, Xia X W, He H, Li S K, Han X, Zhang P, Li G, Zhang P F, Xu J P, Yang Y P, Zhang T C 2019 Phys. Rev. Lett. 123 233604
Google Scholar
[27] Zhang S C, Hu Y Q, Lin G W, Niu Y P, Xia K Y, Gong J B, Gong S Q 2018 Nat. Photonics 12 744
Google Scholar
[28] Lin G W, Zhang S C, Hu Y Q, Niu Y P, Gong J B, Gong S Q 2019 Phys. Rev. Lett. 123 033902
Google Scholar
[29] Zhang Y, Wu J H, Artoni M, La Rocca G C 2021 Opt. Express 29 5890
Google Scholar
[30] Guo T J, Argyropoulos C 2022 Phys. Rev. B 106 235418
Google Scholar
[31] Zheng D D, Zhang Y, Liu Y M, Zhang X J, Wu J H 2023 Phys. Rev. A 107 013704
Google Scholar
[32] Horsley S A R, Artoni M, La Rocca G C 2015 Nat. Photonics 9 436
Google Scholar
[33] Pei X S, Zhang H X, Pan M M, Geng Y, Li T M, Yang H 2023 Opt. Express 31 14694
Google Scholar
[34] Peng P S, Thapa G, Zhou J F, Talbayev D 2023 Optica 10 155
Google Scholar
[35] Guddala S, Kawaguchi Y, Komissarenko F, Kiriushechkina S, Vakulenko A, Chen K, Alù A, Menon V M, Khanikaev A B 2021 Nat. Commun. 12 3746
Google Scholar
[36] Gao W T, Yang C W, Tan Y T, Ren J 2022 Appl. Phys. Lett. 121 071702
Google Scholar
[37] Chamanara N, Taravati S, Deck-Léger Z L, Caloz C 2017 Phys. Rev. B 96 155409
Google Scholar
[38] Hack S A, van der Vegt J J W, Vos W L 2019 Phys. Rev. B 99 115308
Google Scholar
[39] Yoon T, Bajcsy M 2019 Phys. Rev. A 99 023415
Google Scholar
[40] Yang H, Zhang T G, Zhang Y, Wu J H 2020 Phys. Rev. A 101 053856
Google Scholar
[41] Wu J H, Artoni M, La Rocca G C 2017 Phys. Rev. A 95 053862
Google Scholar
[42] Artoni M, La Rocca G C, Bassani F 2005 Phys. Rev. E 72 046604
Google Scholar
[43] Li T M, Wang M H, Yin C P, Wu J H, Yang H 2021 Opt. Express 29 31767
Google Scholar
[44] Yang H, Yang L, Wang X C, Cui C L, Zhang Y, Wu J H 2013 Phys. Rev. A 88 063832
Google Scholar
[45] Wu J H, Artoni M, La Rocca G C 2015 Phys. Rev. A 91 033811
Google Scholar
[46] Chaung Y L, Shamsi A, Abbas M, Ziauddin 2020 Opt. Express 28 1701
Google Scholar
[47] Yang L, Zhang Y, Yan X B, Sheng Y, Cui C L, Wu J H 2015 Phys. Rev. A 92 053859
Google Scholar
[48] Wang D W, Zhou H T, Guo M J, Zhang J X, Evers J, Zhu S Y 2013 Phys. Rev. Lett. 110 093901
Google Scholar
[49] Wang C Q, Jiang X F, Zhao G M, Zhang M Z, Hsu C W, Peng B, Stone A D, Jiang L, Yang L 2020 Nat. Phys. 16 334
Google Scholar
[50] Finkelstein R, Bali S, Firstenberg O, Novikova I 2023 New J. Phys. 25 035001
Google Scholar
[51] 刘建基, 刘甲琛, 张国权 2023 72 094201
Google Scholar
Liu J J, Liu J C, Zhang G Q 2023 Acta Phys. Sin. 72 094201
Google Scholar
[52] Li T M, Yang H, Wang M H, Yin C P, Zhang T G, Zhang Y 2024 Phys. Rev. Res. 6 023122
Google Scholar
[53] Yuan J P, Wu C H, Wang L R, Chen G, Jia S T 2019 Opt. Lett. 44 4123
Google Scholar
[54] Yuan J P, Zhang H F, Wu C H, Wang L R, Xiao L T, Jia S T 2021 Opt. Lett. 46 4184
Google Scholar
[55] Yuan J P, Zhang H F, Wu C H, Chen G, Wang L R, Xiao L T, Jia S T 2023 Laser Photonics Rev. 17 2200667
Google Scholar
[56] Schilke A, Zimmermann C, Guerin W 2012 Phys. Rev. A 86 023809.
Google Scholar
[57] Kuraptsev A S, Sokolov I M 2015 Phys. Rev. A 91 053822
Google Scholar
[58] Artoni M, La Rocca G C 2006 Phys. Rev. Lett. 96 073905
Google Scholar
[59] Zhang Y, Xue Y, Wang G, Cui C L, Wang R, Wu J H 2011 Opt. Express 19 2111
Google Scholar
-
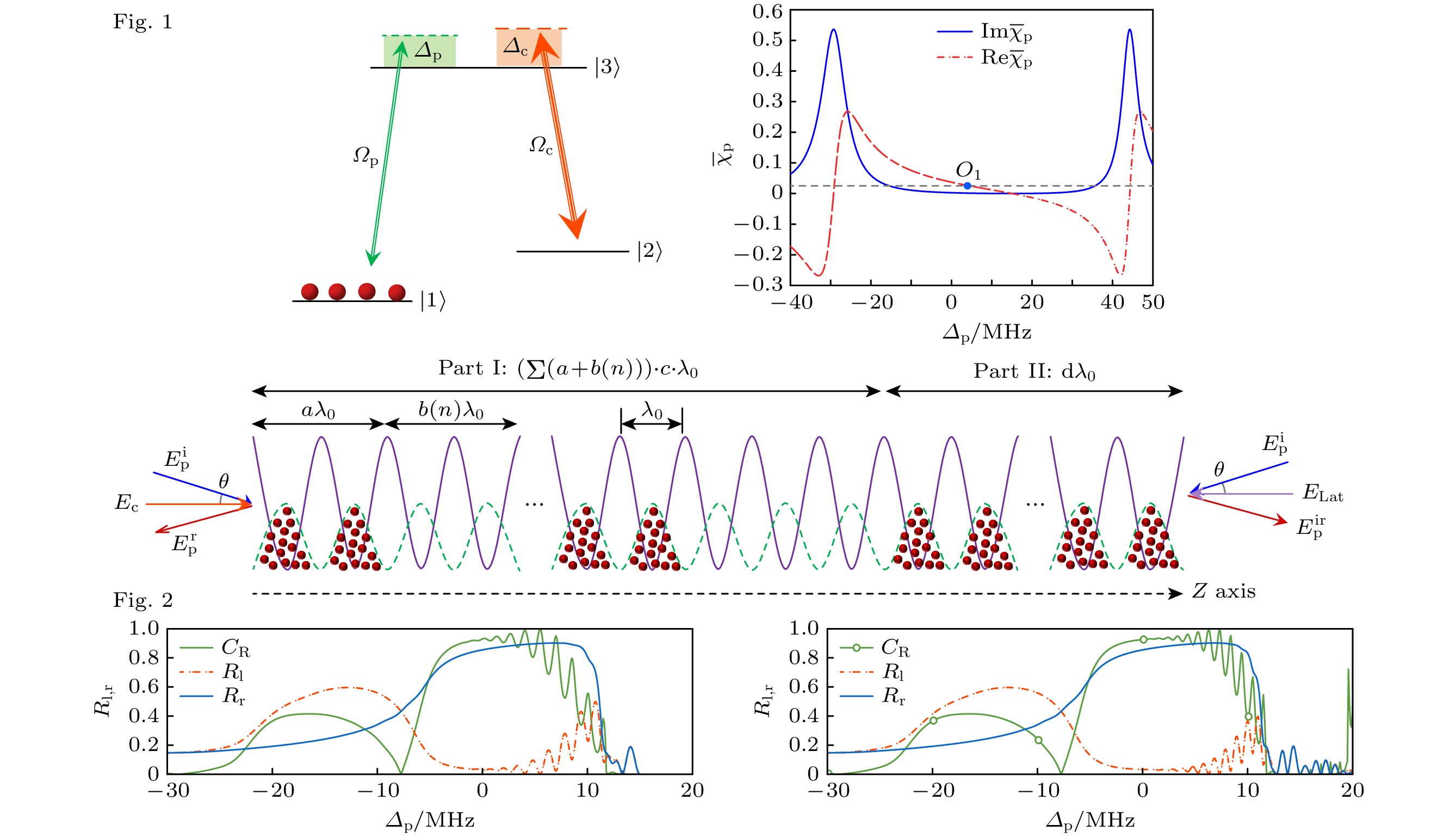
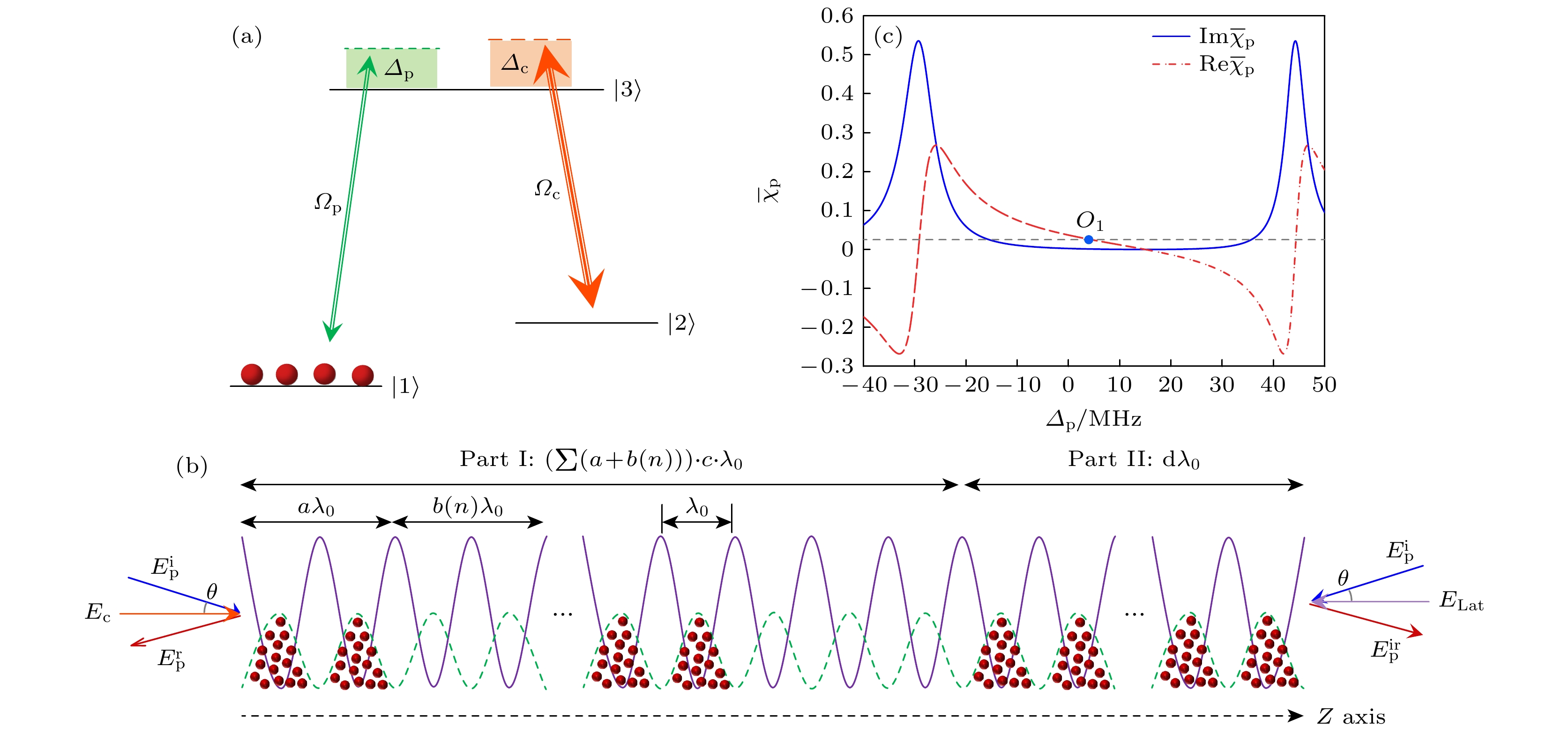
图 1 (a)三能级Lambda型相干原子系统; (b)一维准周期缺陷原子晶格与相干光场的作用; (c)一个满晶格周期中探测场平均极化率实部和虚部随失谐的变化及其与$ - 2\varDelta {\lambda _{{\mathrm{Lat}}}}/{\lambda _{{\mathrm{Lat}}}} \approx 0.0023 $的交点
Fig. 1. (a) Three-level Lambda model coherent atomic system; (b) interaction between 1D quasi-periodic atomic lattice and coherent optical field; (c) the real and imaginary parts of average susceptibility in one filled lattice cell v.s. probe detuning, and the intersection with $ - 2\varDelta {\lambda _{{\text{Lat}}}}/{\lambda _{{\text{Lat}}}} \approx 0.0023 $.
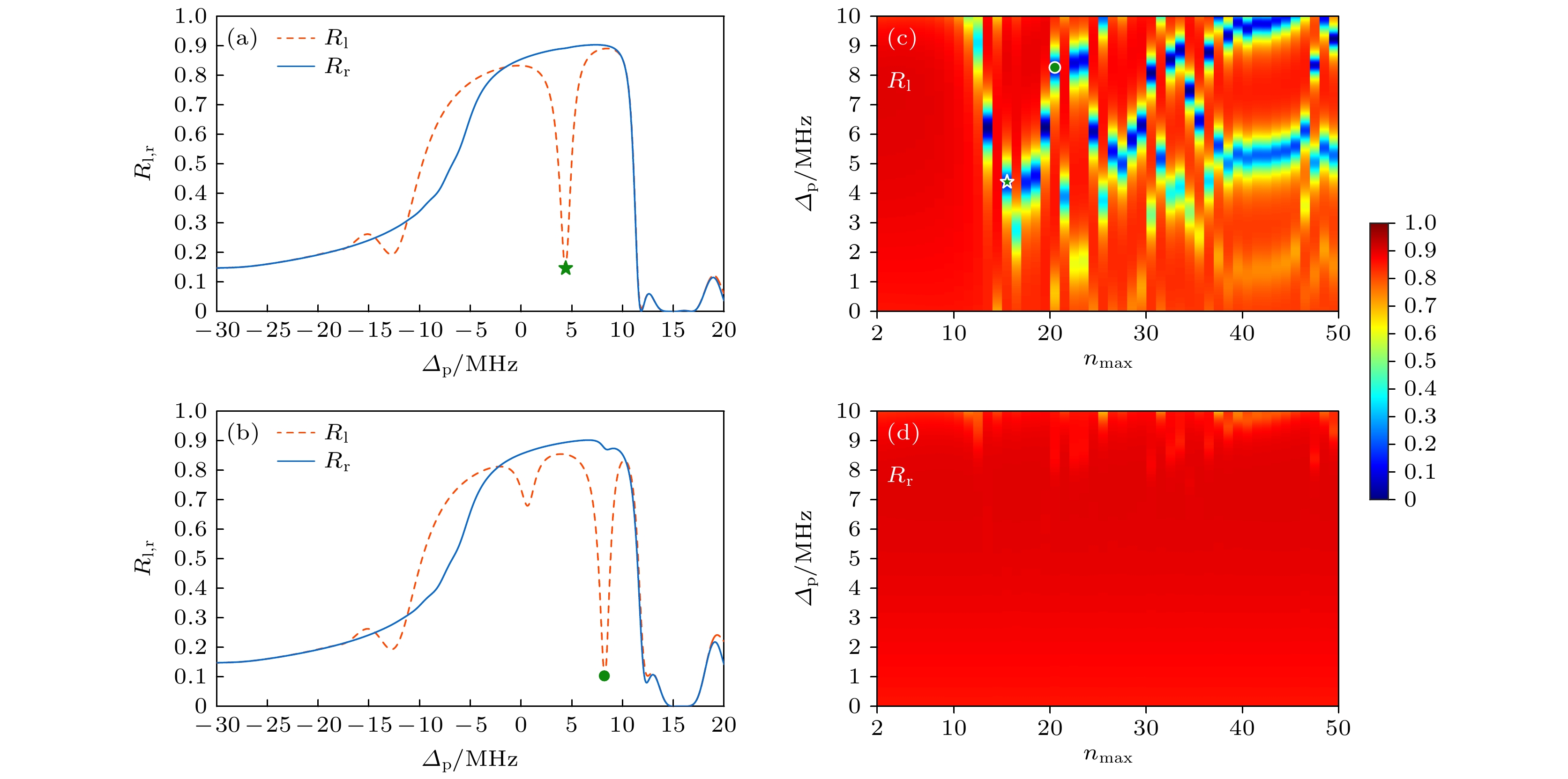
图 2 (a), (b)展示了左右反射率$ {R_{\mathrm{l}}}_{, {\mathrm{r}}} $随失谐$ {\varDelta _{\mathrm{p}}} $的变化, 分别对应$ n \in \left[ {2, 16} \right] $和$ n \in \left[ {2, 21} \right] $; (c), (d)展示了左右反射率$ {R_{\mathrm{l}}}_{, {\mathrm{r}}} $随失谐$ {\varDelta _{\mathrm{p}}} $和斐波那契数列数量$ b(n) $中最大n值的变化. 其他参数: $ {{{N}}_0} = 7 \times {10^{11}}{\text{ }}{\mathrm{c{m}}^{ - 3}} $, $ \eta = 5 $, $ a = 40 $, $ c = 1 $, $ d = 1500 $, $ {\gamma _{31}} = $$ 6{\text{ MHz}} $, $ {\gamma _{21}} = 0.001{\text{ MHz}} $, $ {\varDelta _{\mathrm{c}}} = 15{\text{ MHz}} $, $ {\varOmega _{\mathrm{c}}} = 36{\text{ MHz}} $, $ {\lambda _{{\mathrm{Lat0}}}} = 781{\text{ nm}} $, $ {\lambda _{\mathrm{p}}} = 780.24{\text{ nm}} $, $ \varDelta {\lambda _{{\mathrm{Lat}}}} = - 0.9{\text{ nm}} $, $ {\boldsymbol d} _{13} = 1.0357 \times $$ {10^{ - 29}}{\text{ }}{\mathrm{C}}{ \cdot} {\mathrm{m}} $
Fig. 2. (a) $ n \in \left[ {2, 16} \right] $ and (b) $ n \in \left[ {2, 21} \right] $ shows the reflectivities $ {R_{\mathrm{l}}}_{, {\mathrm{r}}} $ v.s. detuning $ {\varDelta _{\mathrm{p}}} $; (c), (d) the reflectivities $ {R_{\mathrm{l}}}_{, {\mathrm{r}}} $ v.s. the number of dissonance and Fibonacci series $ b(n) $ and detuning $ {\varDelta _{\mathrm{p}}} $, respectively. Other relevant parameters: $ {{{N}}_0} = 7 \times {10^{11}}{\text{ }}{\mathrm{c{m}}^{ - 3}} $, $ \eta = 5 $, $ a = 40 $, $ c = 1 $, $ d = 1500 $, $ {\gamma _{31}} = 6{\text{ MHz}} $, $ {\gamma _{21}} = 0.001{\text{ MHz}} $, $ {\varDelta _{\mathrm{c}}} = 15 \;{\mathrm{MHz}} $, $ {\varOmega _{\mathrm{c}}} = 36{\text{ MHz}} $, $ {\lambda _{{\mathrm{Lat0}}}} = 781{\text{ nm}} $, $ {\lambda _{\mathrm{p}}} = $$ 780.24{\text{ nm}} $, $ \varDelta {\lambda _{{\mathrm{Lat}}}} = - 0.9{\text{ nm}} $, ${\boldsymbol d _{13}}= 1.0357 \times {10^{ - 29}}{\text{ }}{\mathrm{C}} {\cdot} {\mathrm{m}} $.
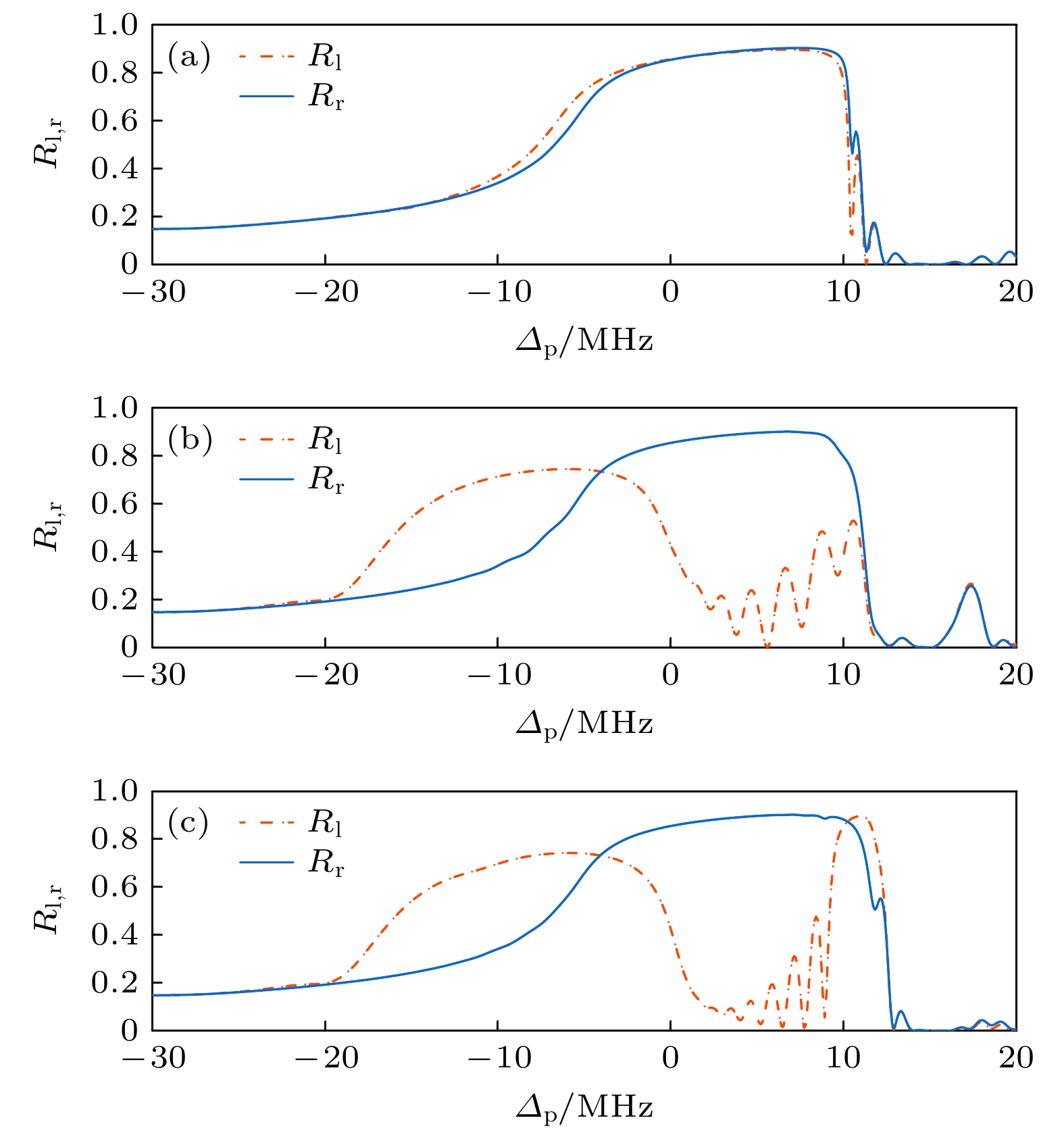
图 3 左右反射率$ {R_{\mathrm{l}}}_{, r} $随失谐$ {\varDelta _{\mathrm{p}}} $的变化(a) $ n \in \left[ {2, 7} \right] $; (b) $ n \in \left[ {8, 13} \right] $; (c) $ n \in \left[ {8, 17} \right] $. 相关参数: $ c = 10 $, 其他参数如图2所示
Fig. 3. The reflectivities $ {R_{\mathrm{l}}}_{, r} $ v.s. detuning $ {\varDelta _{\mathrm{p}}} $: (a) $ n \in $$ \left[ {2, 7} \right] $; (b) $ n \in \left[ {8, 13} \right] $; (c) $ n \in \left[ {8, 17} \right] $. Here $ c = 10 $, other parameters are shown in Fig 2.
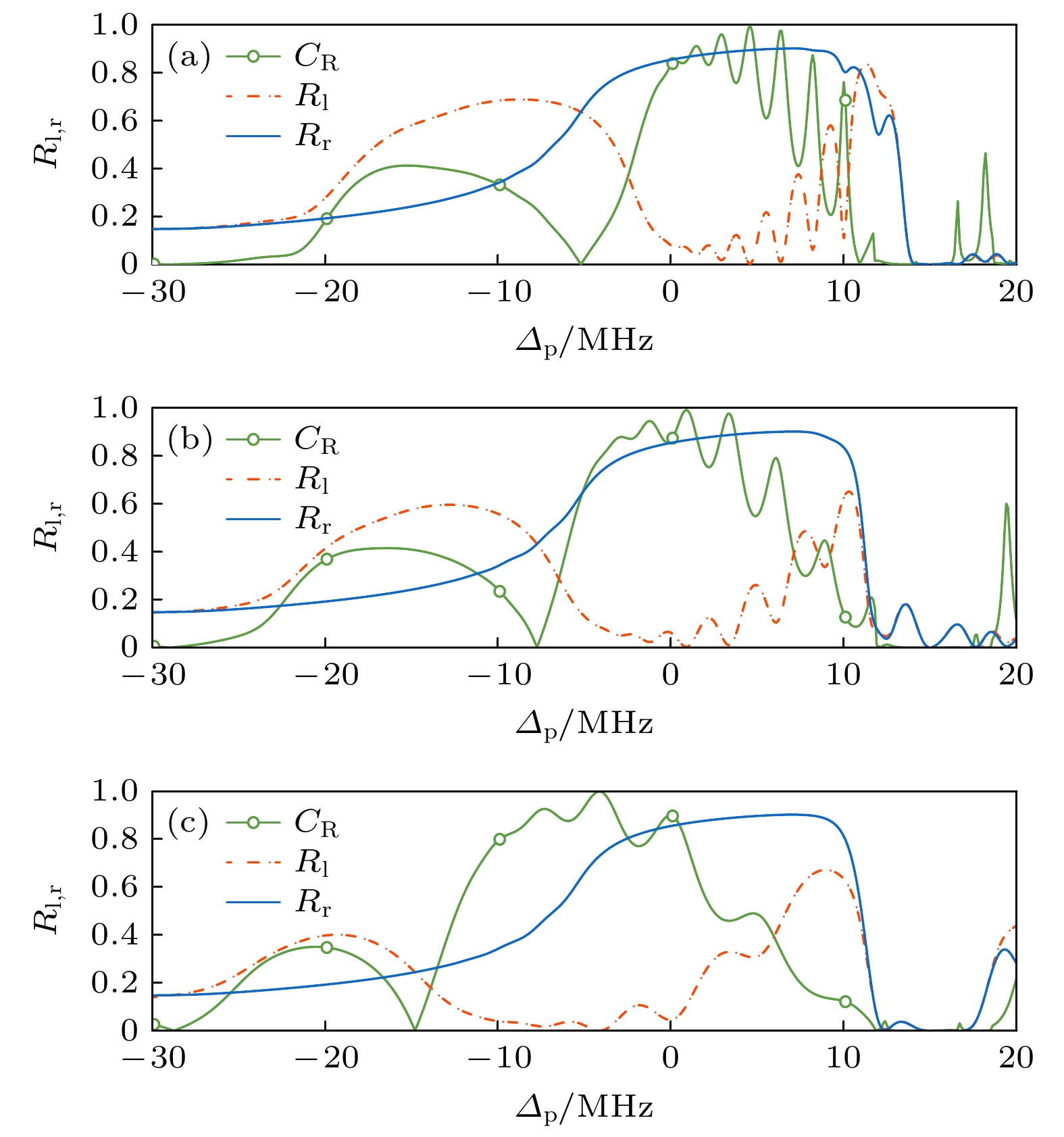
图 4 左右反射率$ {R_{\mathrm{l}}}_{, r} $和反射对比度$ {C_{{R}}} $随失谐$ {\varDelta _{\mathrm{p}}} $的变化 (a) $ a = 30 $; (b) $ a = 20 $; (c) $ a = 10 $. 相关参数: $ n \in $$ \left[ {8, 17} \right] $, $ c = 10 $, 其他参数如图2所示
Fig. 4. The reflectivities $ {R_{\mathrm{l}}}_{, r} $ and the reflection contrast $ {C_{{R}}} $ v.s. detuning $ {\varDelta _{\mathrm{p}}} $: (a) $ a = 30 $; (b) $ a = 20 $; (c) $ a = 10 $. Here $ n \in \left[ {8, 17} \right] $, $ c = 10 $, other parameters are shown in Fig 2.
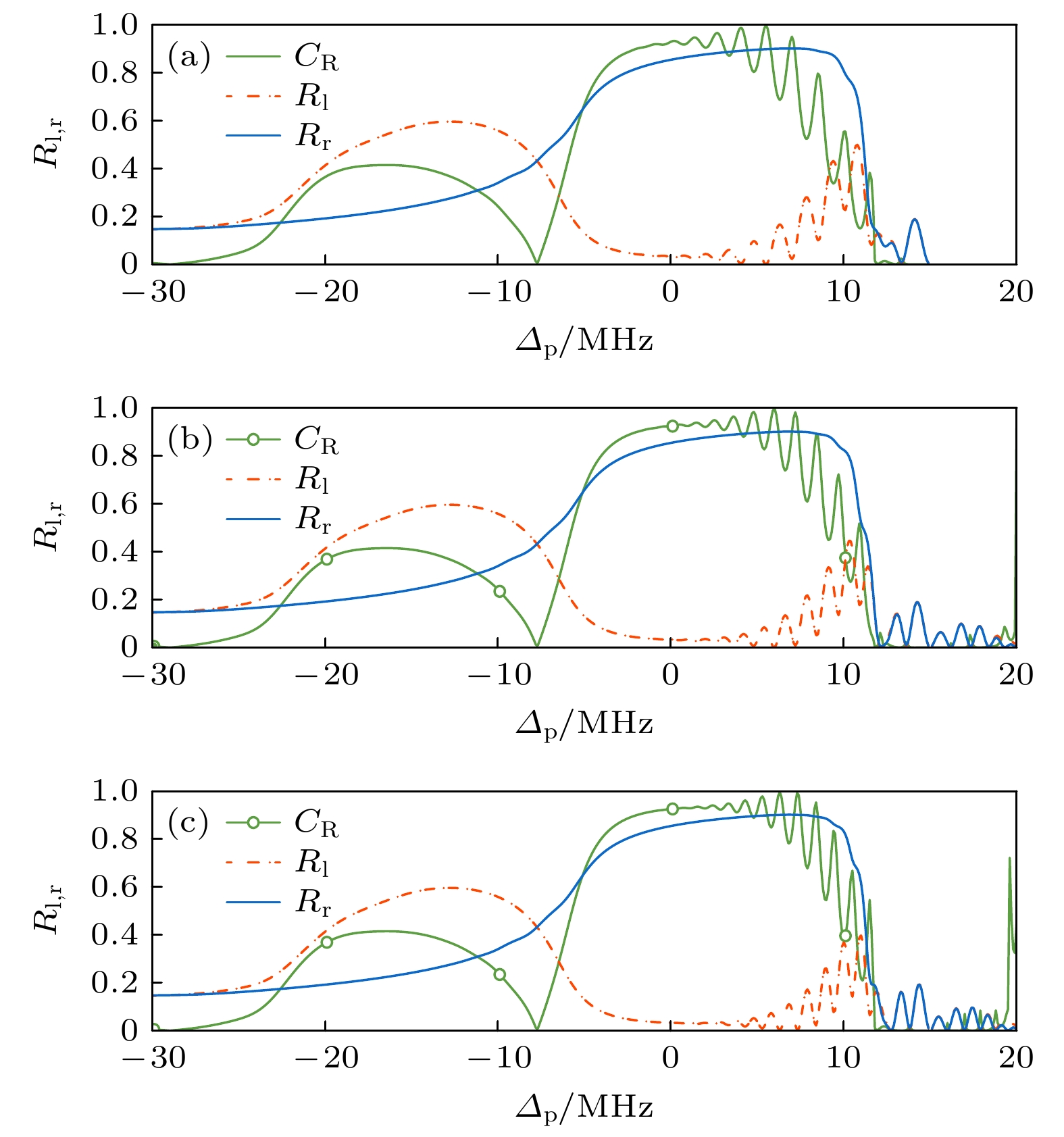
图 5 左右反射率$ {R_{\mathrm{l}}}_{, r} $和反射对比度$ {C_{{R}}} $随失谐$ {\varDelta _{\mathrm{p}}} $的变化 (a) $ c = 20 $; (b) $ c = 25 $; (c) $ c = 30 $. 相关参数: $ n \in $$ \left[ {8, 17} \right] $, $ a = 20 $, 其他参数如图2所示
Fig. 5. The reflectivities $ {R_{\mathrm{l}}}_{, r} $ and the reflection contrast $ {C_{{R}}} $ v.s. detuning $ {\varDelta _{\mathrm{p}}} $: (a) $ c = 20 $; (b) $ c = 25 $; (c) $ c = 30 $. Here $ n \in \left[ {8, 17} \right] $, $ a = 20 $, other parameters are shown in Fig 2.
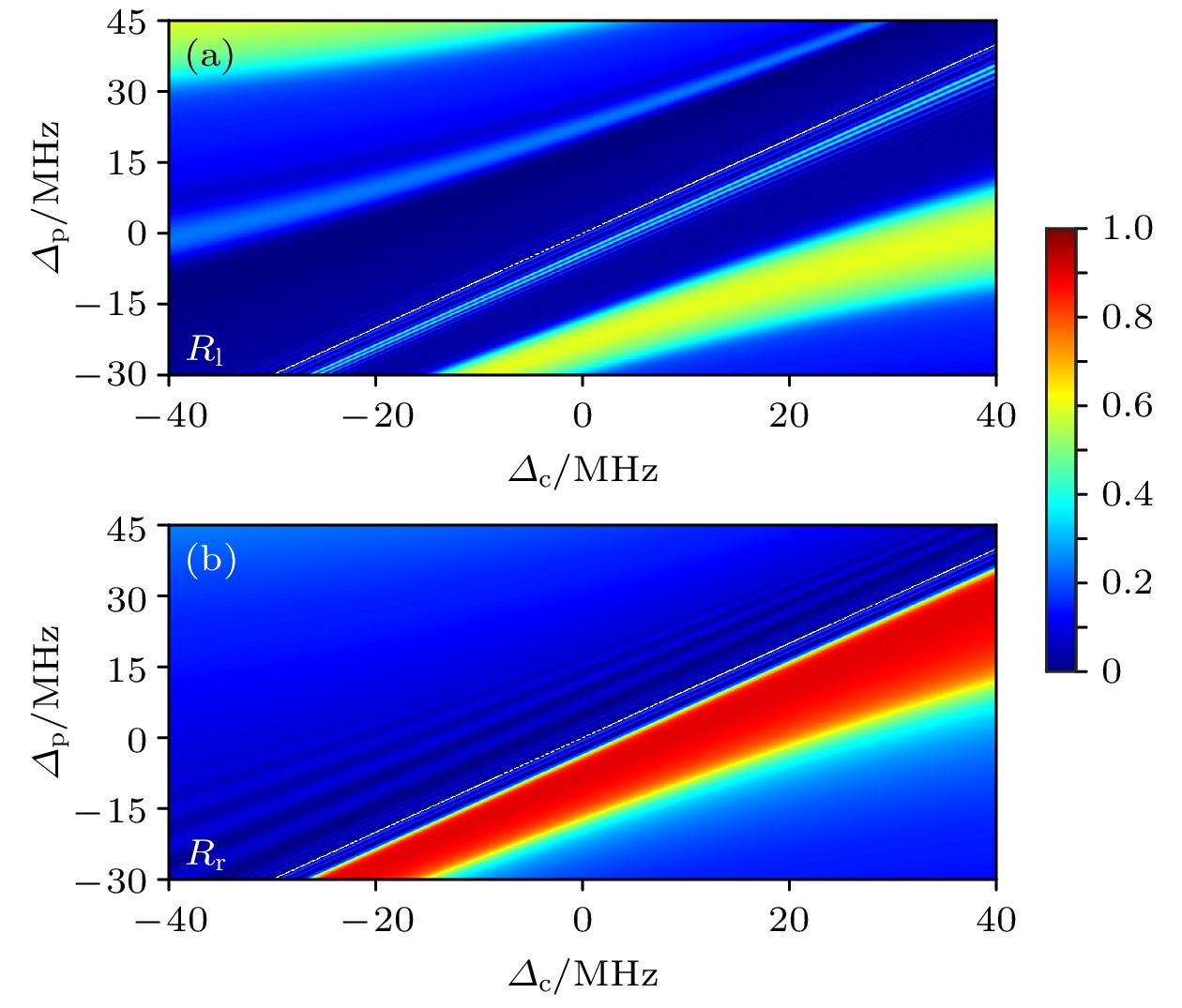
图 6 (a)左反射率$ {R_{\mathrm{l}}} $和(b)右反射率$ {R_{\mathrm{r}}} $随探测场失谐$ {\varDelta _{\mathrm{p}}} $和强耦合场失谐$ {\varDelta _{\mathrm{c}}} $的变化. 相关参数: $ n \in \left[ {8, 17} \right] $, $ a = $$ 20 $, $ c = 30 $, 其他参数如图2所示
Fig. 6. (a) The left reflectivity $ {R_{\mathrm{l}}} $ and (b) the right reflectivity $ {R_{\mathrm{r}}} $ v.s. the probe detuning $ {\varDelta _{\mathrm{p}}} $ and the strong coupling field detuning $ {\varDelta _{\mathrm{c}}} $. Here $ n \in \left[ {8, 17} \right] $, $ a = 20 $, $ c = 30 $, other parameters are shown in Fig 2.
-
[1] White A D, Ahn G H, Gasse K V, Yang K Y, Chang L, Bowers J E, Vučković J 2023 Nat. Photonics 17 143
Google Scholar
[2] Prabu K, Nasre D 2019 Plasmonics 14 1261
Google Scholar
[3] Xia K Y, Nori F, Xiao M 2018 Phys. Rev. Lett. 121 203602
Google Scholar
[4] Tian H, Liu J Q, Siddharth A, Wang R N, Blésin T, He J J, Kippenberg T J, Bhave S A 2021 Nat. Photonics 15 828
Google Scholar
[5] Chan E H W 2014 Opt. Commun. 324 127
Google Scholar
[6] Litinskaya M, Shapiro E A 2015 Phys. Rev. A 91 033802
Google Scholar
[7] Shen H Z, Wang Q, Wang J, Yi X X 2020 Phys. Rev. A 101 013826
Google Scholar
[8] Wu J, Wang Z M, Zhai H, Shi Z X, Wu X H, Wu F 2021 Opt. Mater. Express 11 4058
Google Scholar
[9] Wang Z Y, Qian J, Wang Y P, Li J, You J Q 2023 Appl. Phys. Lett. 123 153904
Google Scholar
[10] Chakraborty S, Das C 2023 Phys. Rev. A 108 063704
Google Scholar
[11] Wang Y M, Xiong W, Xu Z Y, Zhang G Q, You J Q 2022 Sci. China-Phys. , Mech. Astron. 65 260314
Google Scholar
[12] He X W, Wang Z Y, Han X, Zhang S, Wang H F 2023 Opt. Express 31 43506
Google Scholar
[13] Yang Y, Guan B, Zhang C L, Liu L C, Liu K 2020 Optoelectron. Sci. Mater. 11606 74
[14] Kim M K 2015 Opt. Express 23 2040
Google Scholar
[15] Kawaguchi Y, Alù A, Khanikaev A B 2022 Opt. Mater. Express 12 1453
Google Scholar
[16] Sounas D L, Alù A 2017 Nat. Photonics 11 774
Google Scholar
[17] Fleury R, Sounas D L, Alù A 2018 J. Opt. 20 034007
Google Scholar
[18] Cardin A E, Silva S R, Vardeny S R, Padilla W J, Saxena A, Taylor A J, Kort-Kamp W J M, Chen H T, Dalvit D A R, Azad A K 2020 Nat. Commun. 11 1469
Google Scholar
[19] Kittlaus E A, Otterstrom N T, Kharel P, Gertler S, Rakich P T 2018 Nat. Photonics 12 613
Google Scholar
[20] Sohn D B, Kim S, Bahl G 2018 Nat. Photonics 12 91
Google Scholar
[21] Rodriguez S R K, Goblot V, Zambon N C, Amo A, Bloch J 2019 Phys. Rev. A 99 013851
Google Scholar
[22] Shen Z, Zhang Y L, Chen Y, Zou C L, Xiao Y F, Zou X B, Sun F W, Guo G C, Dong C H 2016 Nat. Photonics 10 657
Google Scholar
[23] Ruesink F, Miri M A, Alù A, Verhagen E 2016 Nat. Commun. 7 13662
Google Scholar
[24] Barzanjeh S, Wulf M, Peruzzo M, Kalaee M, Dieterle P B , Painter O, Fink J M 2017 Nat. Commun. 8 953
Google Scholar
[25] Tang L, Tang J S, Chen M Y, Nori F, Xiao M, Xia K Y 2022 Phys. Rev. Lett. 128 083604
Google Scholar
[26] Yang P F, Xia X W, He H, Li S K, Han X, Zhang P, Li G, Zhang P F, Xu J P, Yang Y P, Zhang T C 2019 Phys. Rev. Lett. 123 233604
Google Scholar
[27] Zhang S C, Hu Y Q, Lin G W, Niu Y P, Xia K Y, Gong J B, Gong S Q 2018 Nat. Photonics 12 744
Google Scholar
[28] Lin G W, Zhang S C, Hu Y Q, Niu Y P, Gong J B, Gong S Q 2019 Phys. Rev. Lett. 123 033902
Google Scholar
[29] Zhang Y, Wu J H, Artoni M, La Rocca G C 2021 Opt. Express 29 5890
Google Scholar
[30] Guo T J, Argyropoulos C 2022 Phys. Rev. B 106 235418
Google Scholar
[31] Zheng D D, Zhang Y, Liu Y M, Zhang X J, Wu J H 2023 Phys. Rev. A 107 013704
Google Scholar
[32] Horsley S A R, Artoni M, La Rocca G C 2015 Nat. Photonics 9 436
Google Scholar
[33] Pei X S, Zhang H X, Pan M M, Geng Y, Li T M, Yang H 2023 Opt. Express 31 14694
Google Scholar
[34] Peng P S, Thapa G, Zhou J F, Talbayev D 2023 Optica 10 155
Google Scholar
[35] Guddala S, Kawaguchi Y, Komissarenko F, Kiriushechkina S, Vakulenko A, Chen K, Alù A, Menon V M, Khanikaev A B 2021 Nat. Commun. 12 3746
Google Scholar
[36] Gao W T, Yang C W, Tan Y T, Ren J 2022 Appl. Phys. Lett. 121 071702
Google Scholar
[37] Chamanara N, Taravati S, Deck-Léger Z L, Caloz C 2017 Phys. Rev. B 96 155409
Google Scholar
[38] Hack S A, van der Vegt J J W, Vos W L 2019 Phys. Rev. B 99 115308
Google Scholar
[39] Yoon T, Bajcsy M 2019 Phys. Rev. A 99 023415
Google Scholar
[40] Yang H, Zhang T G, Zhang Y, Wu J H 2020 Phys. Rev. A 101 053856
Google Scholar
[41] Wu J H, Artoni M, La Rocca G C 2017 Phys. Rev. A 95 053862
Google Scholar
[42] Artoni M, La Rocca G C, Bassani F 2005 Phys. Rev. E 72 046604
Google Scholar
[43] Li T M, Wang M H, Yin C P, Wu J H, Yang H 2021 Opt. Express 29 31767
Google Scholar
[44] Yang H, Yang L, Wang X C, Cui C L, Zhang Y, Wu J H 2013 Phys. Rev. A 88 063832
Google Scholar
[45] Wu J H, Artoni M, La Rocca G C 2015 Phys. Rev. A 91 033811
Google Scholar
[46] Chaung Y L, Shamsi A, Abbas M, Ziauddin 2020 Opt. Express 28 1701
Google Scholar
[47] Yang L, Zhang Y, Yan X B, Sheng Y, Cui C L, Wu J H 2015 Phys. Rev. A 92 053859
Google Scholar
[48] Wang D W, Zhou H T, Guo M J, Zhang J X, Evers J, Zhu S Y 2013 Phys. Rev. Lett. 110 093901
Google Scholar
[49] Wang C Q, Jiang X F, Zhao G M, Zhang M Z, Hsu C W, Peng B, Stone A D, Jiang L, Yang L 2020 Nat. Phys. 16 334
Google Scholar
[50] Finkelstein R, Bali S, Firstenberg O, Novikova I 2023 New J. Phys. 25 035001
Google Scholar
[51] 刘建基, 刘甲琛, 张国权 2023 72 094201
Google Scholar
Liu J J, Liu J C, Zhang G Q 2023 Acta Phys. Sin. 72 094201
Google Scholar
[52] Li T M, Yang H, Wang M H, Yin C P, Zhang T G, Zhang Y 2024 Phys. Rev. Res. 6 023122
Google Scholar
[53] Yuan J P, Wu C H, Wang L R, Chen G, Jia S T 2019 Opt. Lett. 44 4123
Google Scholar
[54] Yuan J P, Zhang H F, Wu C H, Wang L R, Xiao L T, Jia S T 2021 Opt. Lett. 46 4184
Google Scholar
[55] Yuan J P, Zhang H F, Wu C H, Chen G, Wang L R, Xiao L T, Jia S T 2023 Laser Photonics Rev. 17 2200667
Google Scholar
[56] Schilke A, Zimmermann C, Guerin W 2012 Phys. Rev. A 86 023809.
Google Scholar
[57] Kuraptsev A S, Sokolov I M 2015 Phys. Rev. A 91 053822
Google Scholar
[58] Artoni M, La Rocca G C 2006 Phys. Rev. Lett. 96 073905
Google Scholar
[59] Zhang Y, Xue Y, Wang G, Cui C L, Wang R, Wu J H 2011 Opt. Express 19 2111
Google Scholar
下载:
计量
- 文章访问数: 314
- PDF下载量: 16
- 被引次数: 0
