-
相互依赖网络中的级联故障过程一直是网络级联分析的一个重要领域. 与以往研究不同的是, 本文考虑了人们在出行时最小化成本的需求, 提出了基于成本约束的网络动力学模型. 同时, 研究了相互依赖网络中不同层次的特性, 定义了不同的负载传播模式. 在此基础上, 本文通过改变网络结构和模型中的参数, 仿真现实中的网络防护策略并验证这些措施的防护效果, 并发现了一些有趣的结论. 一般认为, 增加网络中连边的数量或提高连边的质量可以有效地增强网络的鲁棒性. 然而, 本文的实验结果表明, 这些方法在某些情况下实际上可能会降低网络的鲁棒性. 一方面, 网络中一些特殊边的复活是导致边能力提升网络鲁棒性却下降的主要原因, 因为这些边会破坏原有网络的稳定结构; 另一方面, 无论是提高单层网络的内部连通性来增加网络连边数量, 还是提高相互依赖的网络之间的耦合强度来增加连边数量, 都不能完全有效地提高网络的鲁棒性. 这是因为随着边数量的增加, 网络中可能会出现一些关键边, 这些边会吸引大量的网络负载, 导致网络的鲁棒性下降.Cascading failure process in interdependent networks has always been an important field of network cascading analysis. Unlike the previous studies, we take people’s demand for minimizing travel costs into consideration in this article and propose a network dynamics model based on the cost constraint. On this basis, we pay attention to the characteristics of different layers in the interdependent network, and taking the real-world traffic network for example, we define different load propagation modes for different layers. Then, we carry out the simulation experiment on cascade failure in the artificial network. By changing the structure of the network and the parameters in the model, such as the capability value of the network side and the connectivity of the network, we are able to focus on the effects of traditional protection strategies during the simulation and obtain some interesting conclusions. It is generally believed that increasing the quantity of connections in the network or improving the quality of edges will enhance the network robustness effectively. However, our experimental results show that these methods may actually reduce network robustness in some cases. On the one hand, we find that the resurrection of some special edges in the network is the main reason for the capacity paradox, as these edges will destroy the stable structure of the original network. On the other hand, neither improving the internal connectivity of a single-layer network nor enhancing the coupling strength between interdependent networks will effectively improve network robustness. This is because as the number of edges increases, some critical edges may appear in the network, attracting a large amount of the network load and leading the network robustness to decrease. These conclusions remind us that blindly investing resources in network construction cannot achieve the best protection effect. Only by scientifically designing the network structures and allocating network resources reasonably can the network robustness be effectively improved.
-
Keywords:
- cascading failures /
- interdependent networks /
- robustness /
- capacity paradox
[1] Kinney R, Crucitti P, Albert R, Latora V 2005 Eur. Phys. J. B 46 101
Google Scholar
[2] Glanz J, Perez-Pena R https://www.nytimes.com/2003/08/26/nyregion/90-seconds-that-left-tens-of-millions-of-people-in-the-dark.html [2024-7-17]
[3] Turkey P G https://docs.entsoe.eu/dataset/ops-report-turkey-blackout-march-2015 [2024-7-17]
[4] Li Y F, Sansavini G, Zio E 2013 Reliab. Eng. Syst. Saf. 111 195
Google Scholar
[5] Hamzelou N, Ashtiani M 2019 Future Gener. Comput. Syst. 94 564
Google Scholar
[6] Azzolin A, Dueñas-Osorio L, Cadini F, Zio E 2018 Reliab. Eng. Syst. Saf. 175 196
Google Scholar
[7] Li Z, Guo Y H, Xu G A, Hu Z M 2014 Acta Phys. Sin. 63 158901 (in Chinses) [李钊, 郭燕慧, 徐国爱, 胡正名 2014 63 158901]
Google Scholar
Li Z, Guo Y H, Xu G A, Hu Z M 2014 Acta Phys. Sin. 63 158901 (in Chinses)
Google Scholar
[8] Artime O, Grassia M, De Domenico M, Gleeson J P, Makse H A, Mangioni G, Perc M, Radicchi F 2024 Nat. Rev. Phys. 6 114
Google Scholar
[9] Peng X Z, Yao H, Du J, Wang Z, Ding C 2015 Acta Phys. Sin. 64 048901 (in Chinses) [彭兴钊, 姚宏, 杜军, 王哲, 丁超 2015 64 048901]
Google Scholar
Peng X Z, Yao H, Du J, Wang Z, Ding C 2015 Acta Phys. Sin. 64 048901 (in Chinses)
Google Scholar
[10] Alessandro V 2010 Nature 464 984
Google Scholar
[11] Sun H, Wang H, Yang M, Reniers G 2024 Saf. Sci. 171 106375
Google Scholar
[12] Wu J, You W, Wu T, Xia Y 2018 Physica A 506 451
Google Scholar
[13] Zhang L, Du Y 2023 Reliab. Eng. Syst. Saf. 237 109379
Google Scholar
[14] Wang J, Zhao N, Xiang L, Wang C 2023 Physica A 627 129128
Google Scholar
[15] Zhang Y, Ren W, Feng J, Zhao J, Chen Y, Mi Y 2024 Appl. Energy 371 123655
Google Scholar
[16] Wang J, Zhang C, Huang Y, Xin C 2014 Nonlinear Dyn. 78 37
Google Scholar
[17] Crucitti P, Latora V, Marchiori M 2004 Phys. Rev. E 69 045104
Google Scholar
[18] Albert R, Jeong H, Barabási A L 2000 Nature 406 378
Google Scholar
[19] Li M, Li M, Wu Q, Xu X, Shen J 2024 Electr. Power Syst. Res. 235 110844
Google Scholar
[20] Zhang C, Xu X, Dui H 2020 Reliab. Eng. Syst. Saf. 202 106963
Google Scholar
[21] Wang J, Rong L 2009 Saf. Sci. 47 1332
Google Scholar
[22] Huang S, Li C 2024 Int. J. Electr. Power Energy Syst. 160 110136
Google Scholar
[23] Wang J 2013 Physica A 392 2257
Google Scholar
[24] Dang H, Bai J Z, Lu Y, Li J 2024 Sustainable Cities and Society 114 105749
Google Scholar
[25] Zhou M, Liu J 2014 Physica A 410 131
Google Scholar
[26] Fu X, Xu X, Li W 2024 Physica A 634 129478
Google Scholar
[27] Zhang L, Xu M, Wang S 2023 Reliab. Eng. Syst. Saf. 235 109250
Google Scholar
[28] Zheng K, Liu Y, Wang Y, Wang W 2021 Europhys. Lett. 133 48003
Google Scholar
[29] Dong G, Gao J, Tian L, Du R, He Y 2012 Phys. Rev. E 85 016112
Google Scholar
[30] Wang J, Wang S, Wang Z 2022 Physica A 585 126399
Google Scholar
[31] Goh K I, Lee D S, Kahng B, Kim D 2003 Phys. Rev. Lett. 91 148701
Google Scholar
[32] Lee D S, Goh K I, Kahng B, Kim D 2004 Physica A 338 84
Google Scholar
[33] Watts D J 2002 Proc. Natl. Acad. Sci. U.S.A. 99 5766
Google Scholar
[34] Wang X F, Xu J 2004 Phys. Rev. E 70 056113
Google Scholar
[35] Motter A E, Lai Y C 2002 Phys. Rev. E 66 065102
Google Scholar
[36] Moreno Y, Gómez J B, Pacheco A F 2002 Europhys. Lett. 58 630
Google Scholar
[37] Hamedmoghadam H, Jalili M, Vu H L, Stone L 2021 Nat. Commun. 12 1254
Google Scholar
[38] Albert R, Albert I, Nakarado G L 2004 Phys. Rev. E 69 025103
Google Scholar
[39] Dey P, Mehra R, Kazi F, Wagh S, Singh N M 2016 IEEE Trans. Smart Grid 7 1970
Google Scholar
[40] Xue F, Bompard E, Huang T, Jiang L, Lu S, Zhu H 2017 Physica A 482 728
Google Scholar
[41] Cai Y, Li Y, Cao Y, Li W, Zeng X 2017 Int. J. Electr. Power Energy Syst. 89 106
Google Scholar
[42] Hu Y, Ksherim B, Cohen R, Havlin S 2011 Phys. Rev. E 84 066116
Google Scholar
[43] Tan F, Xia Y, Wei Z 2015 Phys. Rev. E 91 052809.
Google Scholar
[44] Huang X, Gao J, Buldyrev S V, Havlin S, Stanley H E 2011 Phys. Rev. E 83 065101
Google Scholar
[45] Wang S, Hong L, Ouyang M, Zhang J, Chen X 2013 Saf. Sci. 51 328
Google Scholar
[46] Bureau of Public Roads 1964 Traffic Assignment Manual for Application with a Large, High Speed Compute (Oxford University
[47] Wang J, Xu B, Wu Y 2015 Sci. Rep. 5 13939
Google Scholar
[48] Tan S Y, Wu J, Lu L, Li M J, Lu X 2016 Sci. Rep. 6 22916
Google Scholar
[49] Wu J, Barahona M, Tan Y J, Deng H Z 2011 IEEE Trans. Syst. Man Cybern. Part A Syst. Humans 41 1244
Google Scholar
[50] Dai B T, Qin S, Tan S Y, Liu C C, Mou J H, Deng H Z, Liljeros F Z, Lu X 2023 J. Comput. Sci. 69 102030
Google Scholar
[51] Holme P, Kim B J, Yoon C N, Han S K 2002 Phys. Rev. E 65 056109
Google Scholar
-
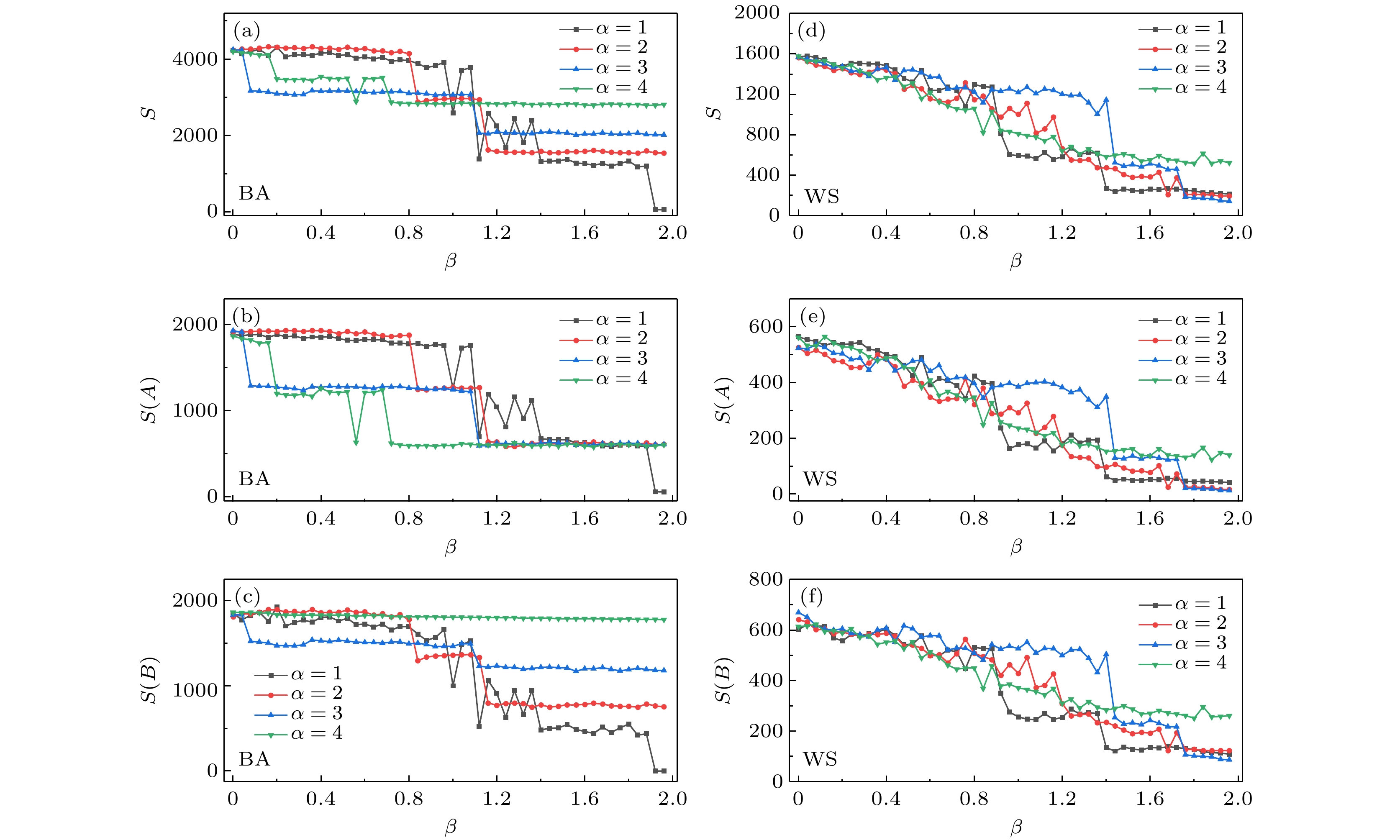
图 2 不同$ \alpha $值下BA与WS网络各自失效边数与$ \beta $值的关系(控制$ \gamma $值为1) (a) 不同$ \alpha $值下BA网络整体失效边数变化情况; (b), (c) 不同$ \alpha $值下BA网络上下层失效边数各自变化情况; (d) 不同$ \alpha $值下WS网络整体失效边数变化情况; (e), (f) 不同$ \alpha $值下WS网络上下层失效边数各自变化情况
Fig. 2. Cascading failures in BA and WS networks for different values of $ \alpha $ ($ \gamma $ is fixed at 1): (a) Cascading failures in BA networks; (b), (c) cascading failures in the upper and lower levels of BA networks; (d) cascading failures in WS networks; (e), (f) cascading failures in the upper and lower levels of WS networks.
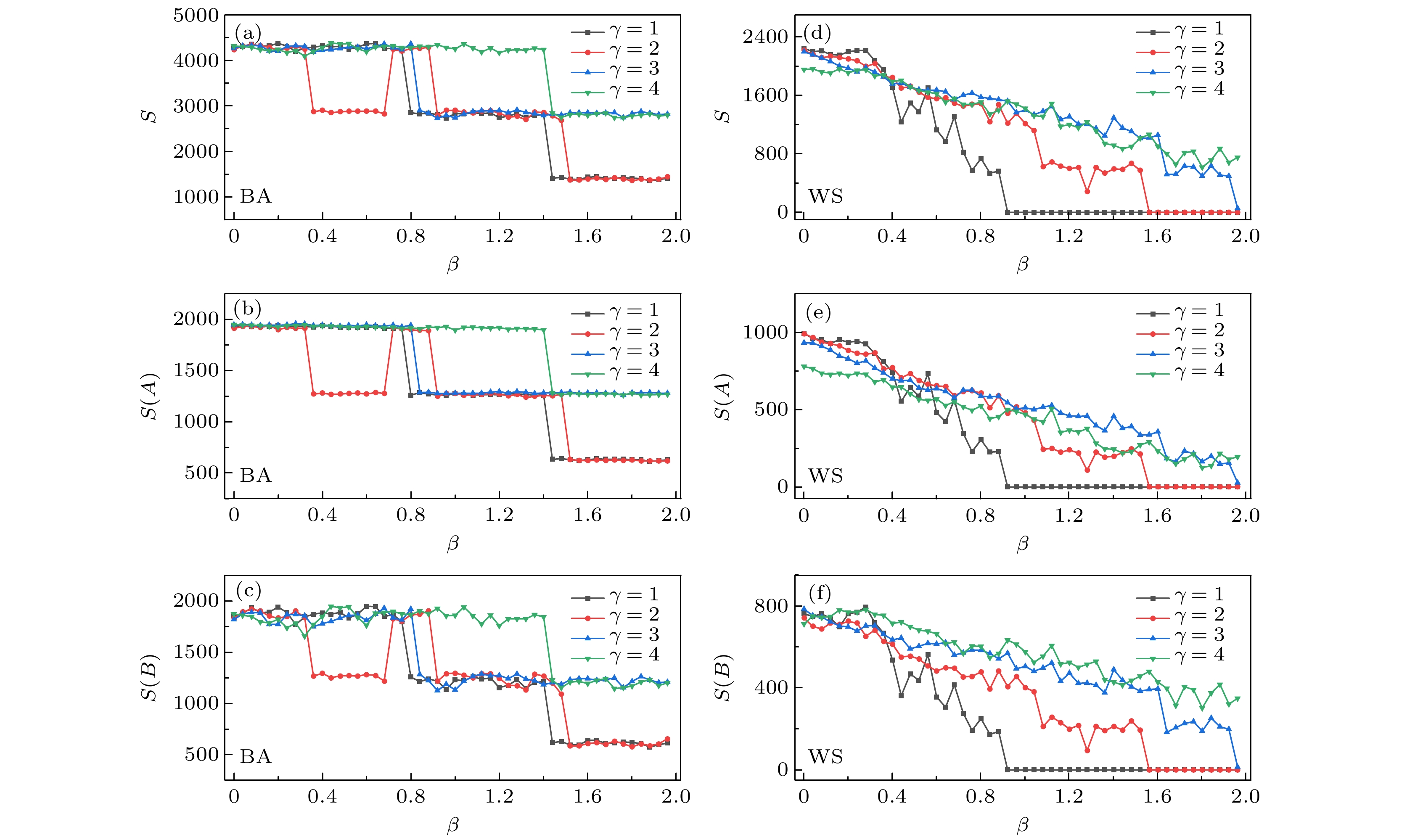
图 3 不同$ \gamma $值下BA与WS网络各自失效边数与$ \beta $值的关系(控制$ \alpha $值为2) (a) 不同$ \gamma $值下BA网络整体失效边数变化情况; (b), (c) 不同$ \gamma $值下BA网络上下层失效边数各自变化情况; (d) 不同$ \gamma $值下WS网络整体失效边数变化情况; (e), (f) 不同$ \gamma $值下WS网络上下层失效边数各自变化情况
Fig. 3. Cascading failures in BA and WS networks for different values of $ \gamma $ ($ \alpha $ is fixed at 2): (a) Cascading failures in BA networks; (b), (c) cascading failures in the upper and lower levels of BA networks; (d) cascading failures in WS networks; (e), (f) cascading failures in the upper and lower levels of WS networks.
图 4 每层12个节点与24条连边的小型人工网络
Fig. 4. Artificial network with 12 nodes and 24 edges on each layer.
图 6 人工网络上层网络$ A $的负载量变化过程 (a)—(d) $ \beta =0. 1 $时的变化情况; (e)—(h) $ \beta =0.2 $时的变化情况; (i)—(l) $ \beta =0. 3 $时的变化情况
Fig. 6. Dynamic change of load on network $ A $: (a)–(d) The situation of $ \beta =0. 1 $; (e)–(h) the situation of $ \beta =0.2 $; (i)–(l) the situation of $ \beta =0. 3 $.
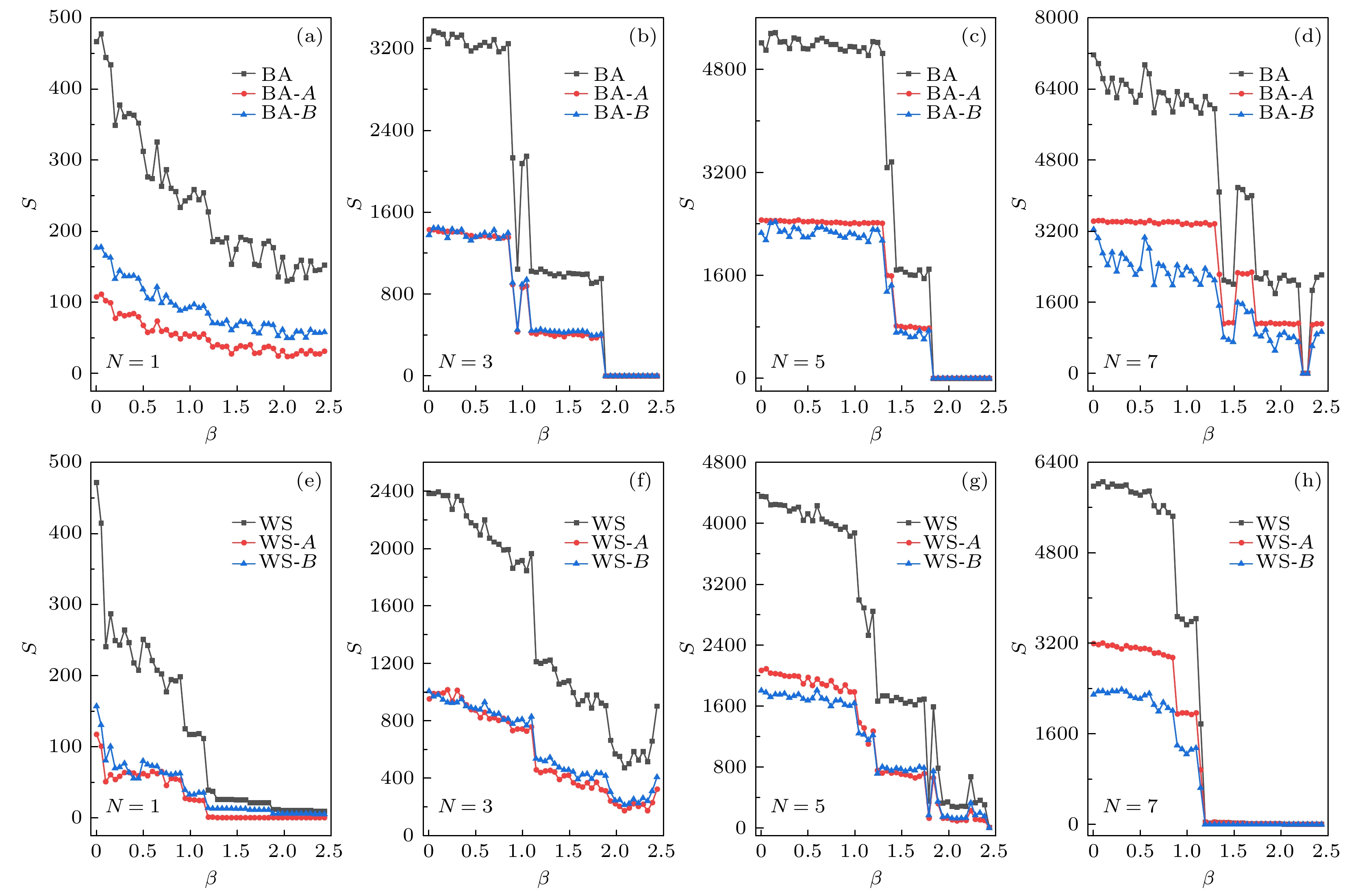
图 7 BA和WS网络中不同$ N{\mathrm{值}} $(网络节点平均度)的级联故障仿真结果(固定$ \alpha $与$ \gamma $) (a)—(d) BA网络的级联故障仿真结果; (e)—(h) WS网络的级联故障仿真结果
Fig. 7. Cascading failure simulation in BA and WS networks with different values of $ N $ ($ \alpha $ and $ \gamma $ are fixed): (a)–(d) Cascading failure simulation in BA networks; (e)–(h) cascading failure simulation in WS networks. N is the average degree of network nodes.
图 8 网络中失效边数百分比与$ N $值的关系(固定$ \alpha $与$ \gamma $) (a) BA网络的仿真结果; (b) WS网络的仿真结果
Fig. 8. Correlation between $ N $ and the percentage of failed edges ($ \alpha $ and $ \gamma $ are fixed): (a) Simulation in BA networks; (b) simulation in WS networks.
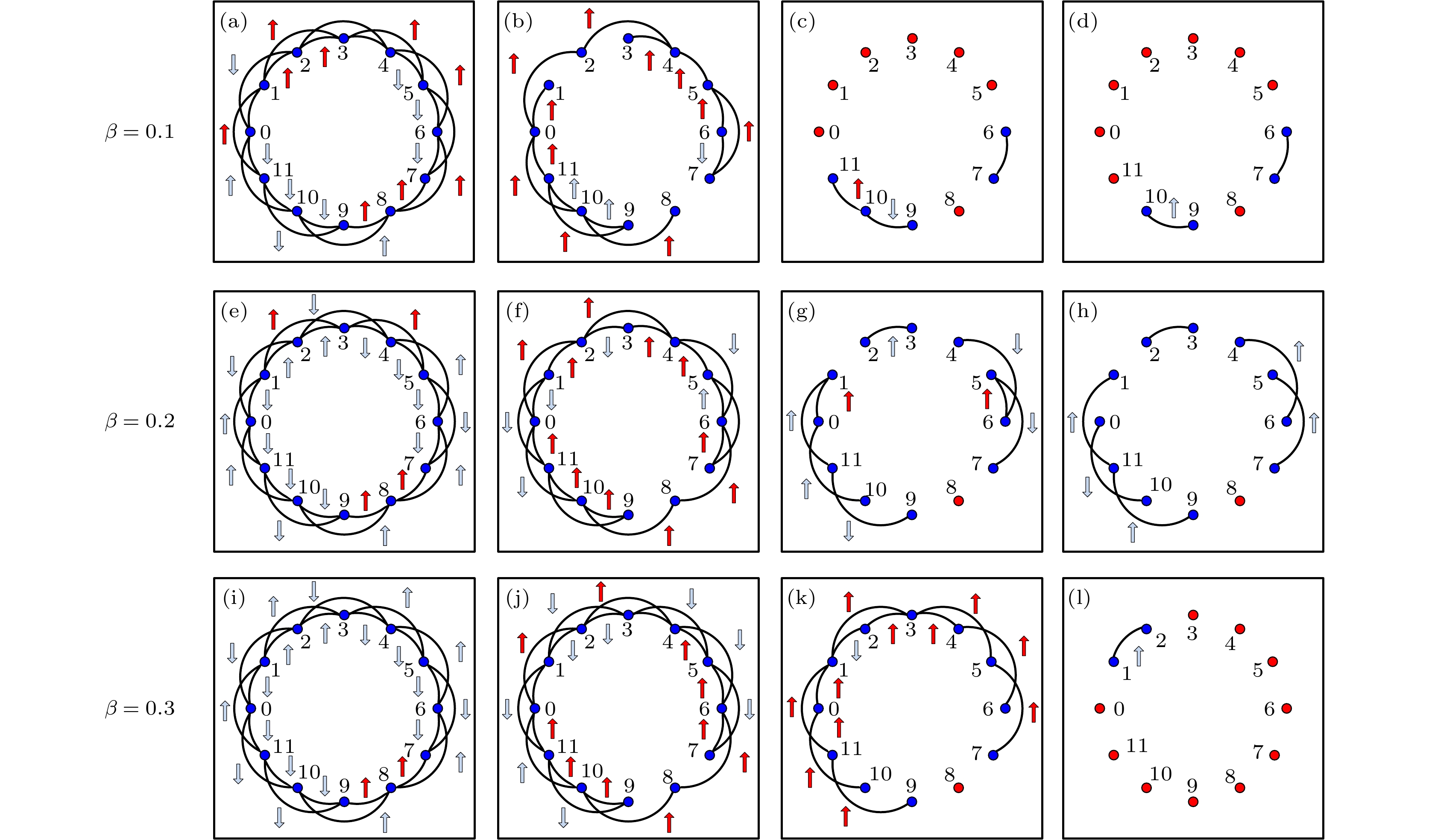
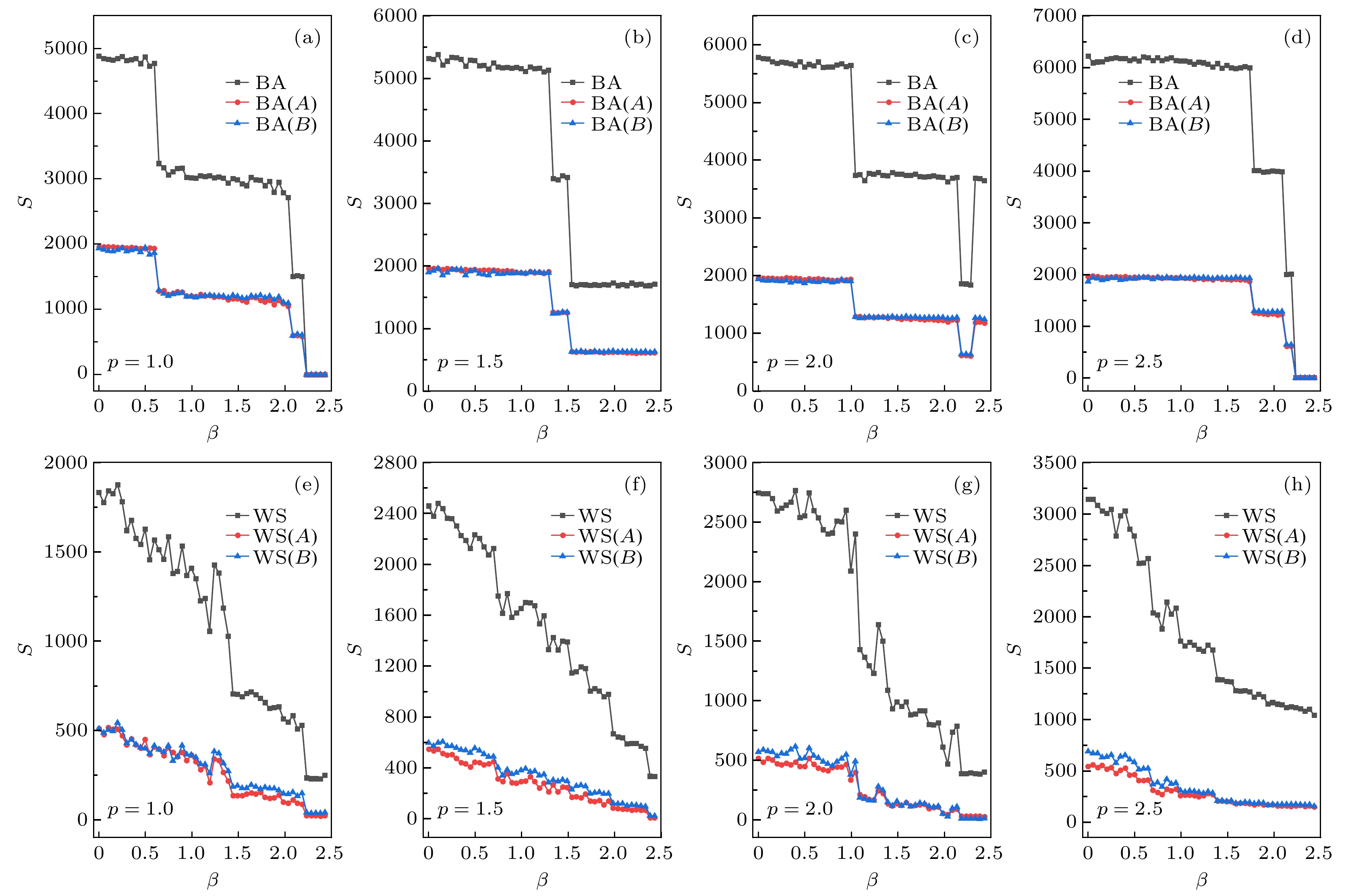
图 11 BA和WS网络中不同$ p $值(网络耦合强度)的级联故障仿真结果(固定$ \alpha $与$ \gamma $) (a)—(d) BA网络的级联故障仿真结果; (e)—(h) WS网络的级联故障仿真结果
Fig. 11. Cascading failure simulation in BA and WS networks with different values of $ p $ (coupling strength) ($ \alpha $ and $ \gamma $ are fixed): (a)–(d) Cascading failure simulation in BA networks; (e)–(h) cascading failure simulation in WS networks.
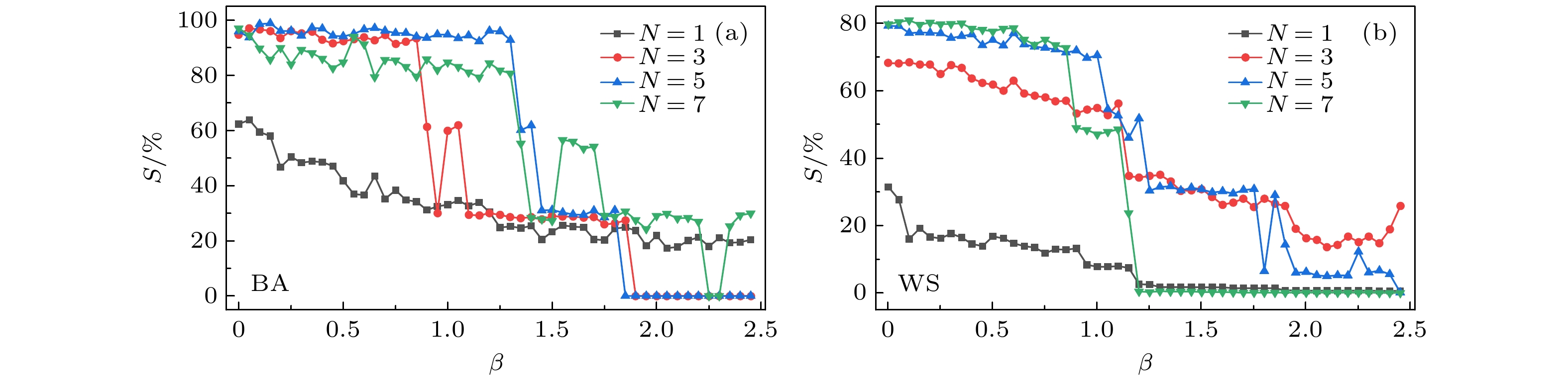
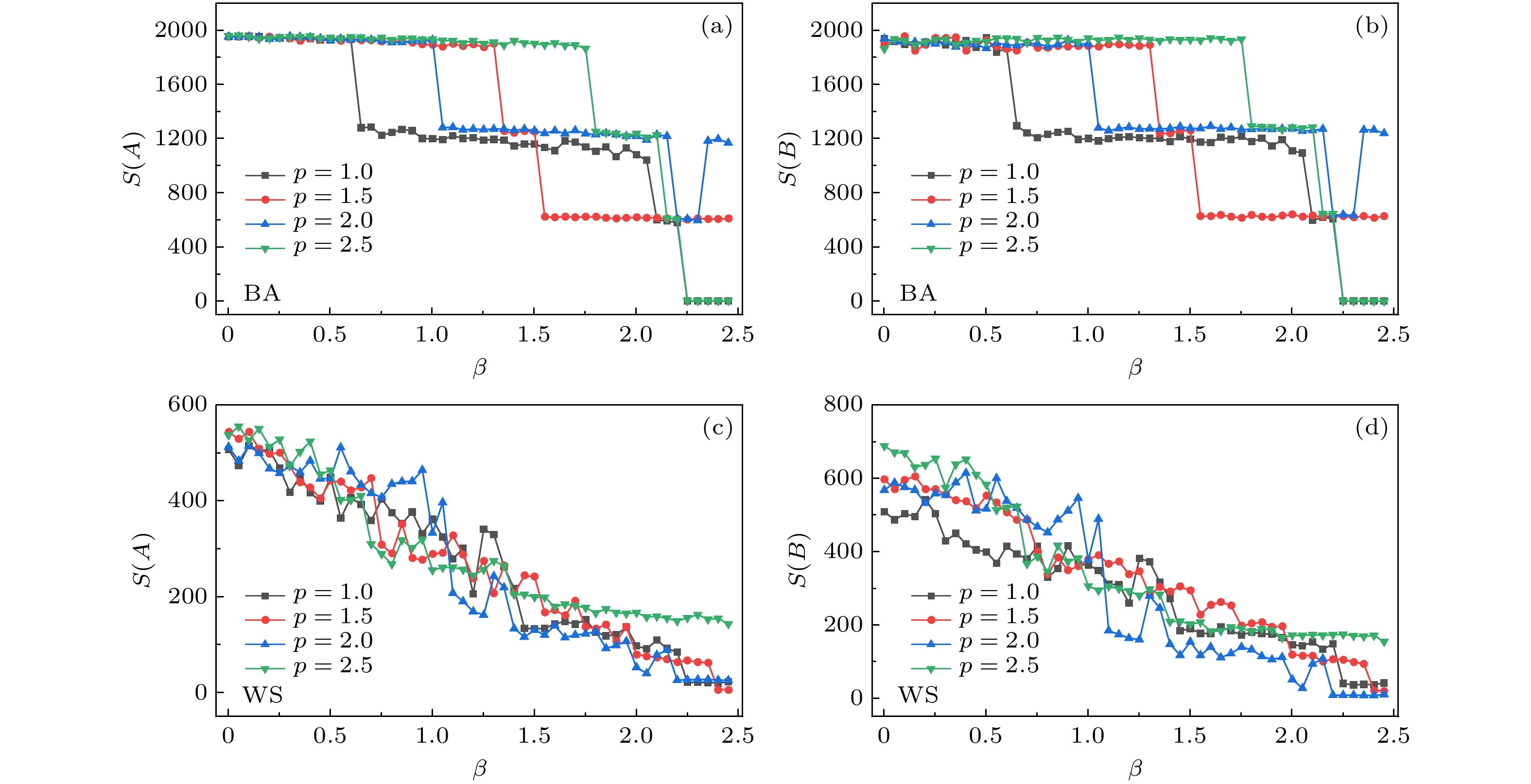
图 12 不同网络层中$ p $值变化对网络级联故障结果的影响(固定$ \alpha $与$ \gamma $) (a) BA上层网络的级联故障仿真结果; (b) BA下层网络的级联故障仿真结果; (c) WS上层网络的级联故障仿真结果; (d) WS下层网络的级联故障仿真结果
Fig. 12. Correlation between $ p $ and failed edges in different layers ($ \alpha $ and $ \gamma $ are fixed): (a) Results of the upper layer of BA networks; (b) results of the lower layer of BA networks; (c) results of the upper layer of WS networks; (d) results of the lower layer of WS networks.
表 1 级联故障模型组件和过程定义
Table 1. Definition of cascading failure model component and process.
组件或过程 定义方式 负载流动过程 $ {F}_{i\to j}={F}_{i\to }\cdot \dfrac{{\omega }_{j}/{t}_{ij}^{\gamma }}{\displaystyle\sum\limits_{n\in N\cap n\ne i}^{N} \dfrac{{\omega }_{n}}{{t}_{in}^{\gamma }}} $ 边初始负载 $ {L}_{m}\left(0\right)=\displaystyle \sum\limits_{i, j\in N}{F}_{i\to j}\cdot {R}_{m}^{i, j} $ 边能力 $ {C}_{m}=\left(1+\beta \right){L}_{m}\left(0\right), m\in E $ 级联失效过程 若$ {L}_{m}\left(T\right) > {C}_{m} $, 则删除边$ m $ 鲁棒性统计指标 失效边数$ S $ 
下载: 导出CSV
表 2 BA和WS网络上层网络A失效边数百分比与$ \alpha $值变化对应关系
Table 2. Correlation between $ \alpha $ and the percentage of failed edges in the upper layer A of BA and WS network.
$ \alpha $ = 1 $ \alpha $ = 2 $ \alpha $ = 3 $ \alpha $ = 4 $ {\mathrm{B}}{\mathrm{A}} $ 55.25% 47.61% 40.67% 31.03% $ {\mathrm{W}}{\mathrm{S}} $ 39.33% 35.54% 40.37% 38.92%
下载: 导出CSV
表 3 BA和WS网络上层网络A负载量百分比与$ \alpha $值变化对应关系
Table 3. Correlation between $ \alpha $ and the percentage of loads in the upper layer A of BA and WS network.
$ \alpha $ = 1 $ \alpha $ = 2 $ \alpha $ = 3 $ \alpha $ = 4 $ {\mathrm{B}}{\mathrm{A}} $ 60.74% 52.41% 46.83% 44.11% $ {\mathrm{W}}{\mathrm{S}} $ 45.54% 46.70% 43.69% 41.15%
下载: 导出CSV
表 4 BA和WS网络上层网络A通行时间平均值与$ \alpha $值变化对应关系(假定每条边长度为1)
Table 4. Correlation between $ \alpha $ and the passage time in the upper layer A of BA and WS network (with the length of each edge equals to 1).
$ \alpha $ = 1 $ \alpha $ = 2 $ \alpha $ = 3 $ \alpha $ = 4 $ {\mathrm{B}}{\mathrm{A}} $ 1.0454 1.0762 1.0968 1.1375 $ {\mathrm{W}}{\mathrm{S}} $ 1.1124 1.1287 1.0962 1.0931
下载: 导出CSV
表 5 BA和WS网络上层网络A失效边数百分比与$ \gamma $值变化对应关系(当$ \alpha =2 $)
Table 5. Correlation between $ \gamma $ and the percentage of failed edges in the upper layer A of BA and WS network when $ \alpha =2 $.
$ \gamma $ = 1 $ \gamma $ = 2 $ \gamma $ = 3 $ \gamma $ = 4 $ {\mathrm{B}}{\mathrm{A}} $ 50.85% 50.59% 51.25% 52.20% $ {\mathrm{W}}{\mathrm{S}} $ 56.30% 55.64% 50.71% 42.02%
下载: 导出CSV
表 6 BA和WS网络上层网络A失效边数百分比与$ \gamma $值变化对应关系(当$ \alpha =0 $)
Table 6. Correlation between $ \gamma $ and the percentage of failed edges in the upper layer A of BA and WS network when $ \alpha =0 $.
$ \gamma $ = 1 $ \gamma $ = 2 $ \gamma $ = 3 $ \gamma $ = 4 $ {\mathrm{B}}{\mathrm{A}} $ 50.63% 52.21% 55.84% 57.16% $ {\mathrm{W}}{\mathrm{S}} $ 48.15% 49.32% 55.47% 58.94%
下载: 导出CSV
表 7 BA网络聚类系数与网络不平均分配指数及失效边数占比变化对应关系
Table 7. Corresponding values of unequal distribution index and the proportion of failure edges with the change of clustering coefficient in BA network.
聚类系数 0.2311 0.4647 0.6536 不平均分配指数 0.637 0.819 0.845 失效边数占比/% 59.80 84.72 84.70
下载: 导出CSV
表 8 WS网络聚类系数与网络不平均分配指数及失效边数占比变化对应关系
Table 8. Corresponding values of unequal distribution index and the proportion of failure edges with the change of clustering coefficient in WS network.
聚类系数 0.2149 0.3681 0.4276 不平均分配指数 0.452 0.611 0.656 失效边数占比/% 54.78 70.46 67.07
下载: 导出CSV
-
[1] Kinney R, Crucitti P, Albert R, Latora V 2005 Eur. Phys. J. B 46 101
Google Scholar
[2] Glanz J, Perez-Pena R https://www.nytimes.com/2003/08/26/nyregion/90-seconds-that-left-tens-of-millions-of-people-in-the-dark.html [2024-7-17]
[3] Turkey P G https://docs.entsoe.eu/dataset/ops-report-turkey-blackout-march-2015 [2024-7-17]
[4] Li Y F, Sansavini G, Zio E 2013 Reliab. Eng. Syst. Saf. 111 195
Google Scholar
[5] Hamzelou N, Ashtiani M 2019 Future Gener. Comput. Syst. 94 564
Google Scholar
[6] Azzolin A, Dueñas-Osorio L, Cadini F, Zio E 2018 Reliab. Eng. Syst. Saf. 175 196
Google Scholar
[7] Li Z, Guo Y H, Xu G A, Hu Z M 2014 Acta Phys. Sin. 63 158901 (in Chinses) [李钊, 郭燕慧, 徐国爱, 胡正名 2014 63 158901]
Google Scholar
Li Z, Guo Y H, Xu G A, Hu Z M 2014 Acta Phys. Sin. 63 158901 (in Chinses)
Google Scholar
[8] Artime O, Grassia M, De Domenico M, Gleeson J P, Makse H A, Mangioni G, Perc M, Radicchi F 2024 Nat. Rev. Phys. 6 114
Google Scholar
[9] Peng X Z, Yao H, Du J, Wang Z, Ding C 2015 Acta Phys. Sin. 64 048901 (in Chinses) [彭兴钊, 姚宏, 杜军, 王哲, 丁超 2015 64 048901]
Google Scholar
Peng X Z, Yao H, Du J, Wang Z, Ding C 2015 Acta Phys. Sin. 64 048901 (in Chinses)
Google Scholar
[10] Alessandro V 2010 Nature 464 984
Google Scholar
[11] Sun H, Wang H, Yang M, Reniers G 2024 Saf. Sci. 171 106375
Google Scholar
[12] Wu J, You W, Wu T, Xia Y 2018 Physica A 506 451
Google Scholar
[13] Zhang L, Du Y 2023 Reliab. Eng. Syst. Saf. 237 109379
Google Scholar
[14] Wang J, Zhao N, Xiang L, Wang C 2023 Physica A 627 129128
Google Scholar
[15] Zhang Y, Ren W, Feng J, Zhao J, Chen Y, Mi Y 2024 Appl. Energy 371 123655
Google Scholar
[16] Wang J, Zhang C, Huang Y, Xin C 2014 Nonlinear Dyn. 78 37
Google Scholar
[17] Crucitti P, Latora V, Marchiori M 2004 Phys. Rev. E 69 045104
Google Scholar
[18] Albert R, Jeong H, Barabási A L 2000 Nature 406 378
Google Scholar
[19] Li M, Li M, Wu Q, Xu X, Shen J 2024 Electr. Power Syst. Res. 235 110844
Google Scholar
[20] Zhang C, Xu X, Dui H 2020 Reliab. Eng. Syst. Saf. 202 106963
Google Scholar
[21] Wang J, Rong L 2009 Saf. Sci. 47 1332
Google Scholar
[22] Huang S, Li C 2024 Int. J. Electr. Power Energy Syst. 160 110136
Google Scholar
[23] Wang J 2013 Physica A 392 2257
Google Scholar
[24] Dang H, Bai J Z, Lu Y, Li J 2024 Sustainable Cities and Society 114 105749
Google Scholar
[25] Zhou M, Liu J 2014 Physica A 410 131
Google Scholar
[26] Fu X, Xu X, Li W 2024 Physica A 634 129478
Google Scholar
[27] Zhang L, Xu M, Wang S 2023 Reliab. Eng. Syst. Saf. 235 109250
Google Scholar
[28] Zheng K, Liu Y, Wang Y, Wang W 2021 Europhys. Lett. 133 48003
Google Scholar
[29] Dong G, Gao J, Tian L, Du R, He Y 2012 Phys. Rev. E 85 016112
Google Scholar
[30] Wang J, Wang S, Wang Z 2022 Physica A 585 126399
Google Scholar
[31] Goh K I, Lee D S, Kahng B, Kim D 2003 Phys. Rev. Lett. 91 148701
Google Scholar
[32] Lee D S, Goh K I, Kahng B, Kim D 2004 Physica A 338 84
Google Scholar
[33] Watts D J 2002 Proc. Natl. Acad. Sci. U.S.A. 99 5766
Google Scholar
[34] Wang X F, Xu J 2004 Phys. Rev. E 70 056113
Google Scholar
[35] Motter A E, Lai Y C 2002 Phys. Rev. E 66 065102
Google Scholar
[36] Moreno Y, Gómez J B, Pacheco A F 2002 Europhys. Lett. 58 630
Google Scholar
[37] Hamedmoghadam H, Jalili M, Vu H L, Stone L 2021 Nat. Commun. 12 1254
Google Scholar
[38] Albert R, Albert I, Nakarado G L 2004 Phys. Rev. E 69 025103
Google Scholar
[39] Dey P, Mehra R, Kazi F, Wagh S, Singh N M 2016 IEEE Trans. Smart Grid 7 1970
Google Scholar
[40] Xue F, Bompard E, Huang T, Jiang L, Lu S, Zhu H 2017 Physica A 482 728
Google Scholar
[41] Cai Y, Li Y, Cao Y, Li W, Zeng X 2017 Int. J. Electr. Power Energy Syst. 89 106
Google Scholar
[42] Hu Y, Ksherim B, Cohen R, Havlin S 2011 Phys. Rev. E 84 066116
Google Scholar
[43] Tan F, Xia Y, Wei Z 2015 Phys. Rev. E 91 052809.
Google Scholar
[44] Huang X, Gao J, Buldyrev S V, Havlin S, Stanley H E 2011 Phys. Rev. E 83 065101
Google Scholar
[45] Wang S, Hong L, Ouyang M, Zhang J, Chen X 2013 Saf. Sci. 51 328
Google Scholar
[46] Bureau of Public Roads 1964 Traffic Assignment Manual for Application with a Large, High Speed Compute (Oxford University
[47] Wang J, Xu B, Wu Y 2015 Sci. Rep. 5 13939
Google Scholar
[48] Tan S Y, Wu J, Lu L, Li M J, Lu X 2016 Sci. Rep. 6 22916
Google Scholar
[49] Wu J, Barahona M, Tan Y J, Deng H Z 2011 IEEE Trans. Syst. Man Cybern. Part A Syst. Humans 41 1244
Google Scholar
[50] Dai B T, Qin S, Tan S Y, Liu C C, Mou J H, Deng H Z, Liljeros F Z, Lu X 2023 J. Comput. Sci. 69 102030
Google Scholar
[51] Holme P, Kim B J, Yoon C N, Han S K 2002 Phys. Rev. E 65 056109
Google Scholar
下载:
计量
- 文章访问数: 490
- PDF下载量: 31
- 被引次数: 0
