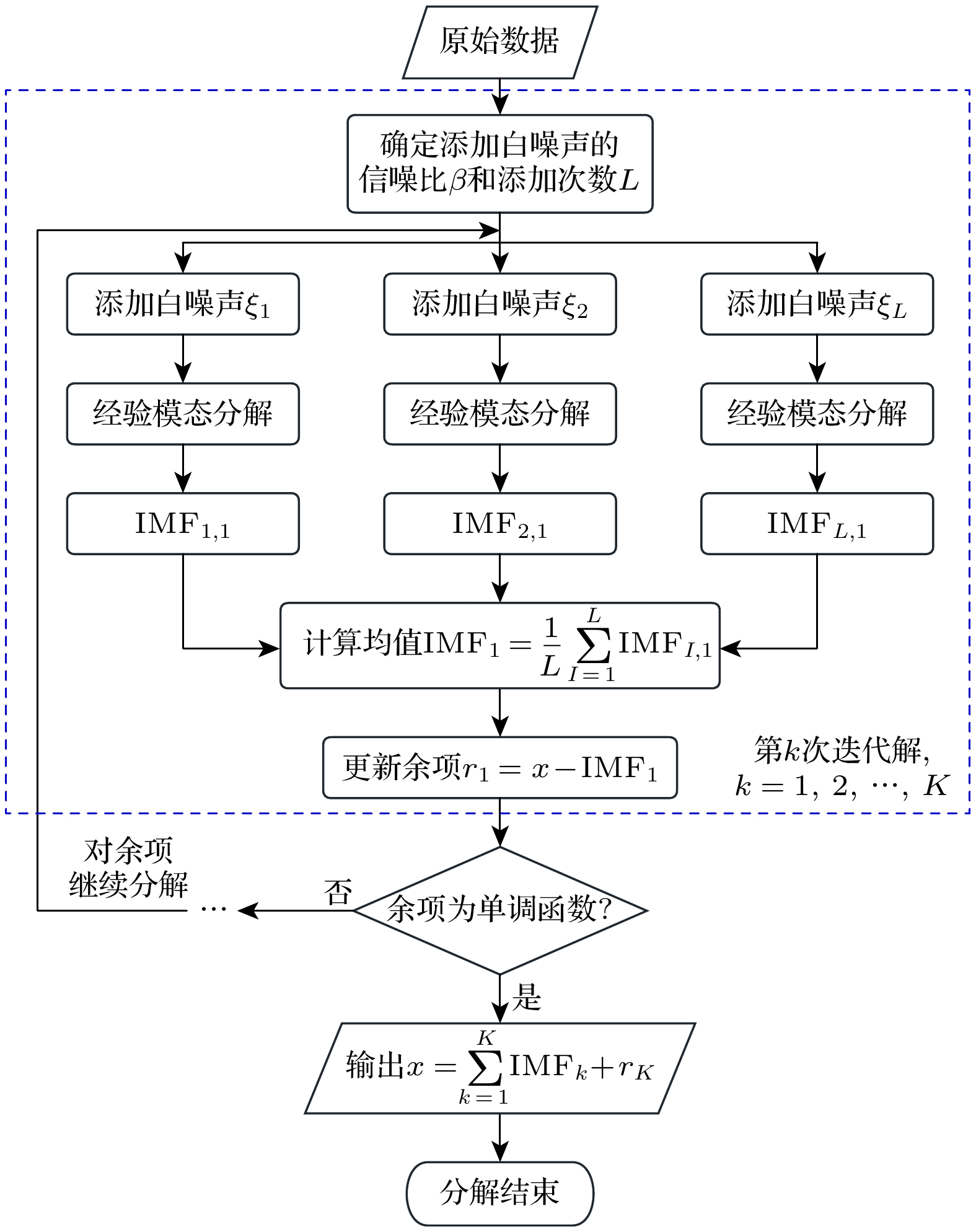
-
为研究地球自转速率变化的非线性特性, 结合自适应噪声完备经验模态分解、定量递归分析和Grassberger-Procaccia算法, 从周期、混沌和分形多角度对1962年1月1日至2023年12月31日反映地球自转速率变化的日长变化(length of day, ΔLOD)观测序列的非线性特性进行全面分析, 并着重对比分析扣除周期成分或混沌成分前后ΔLOD特性是否存在明显区别. 主要结论如下: 1) ΔLOD时间序列由趋势成分、周期成分和混沌成分构成, 具有明显的多时间尺度、混沌动力学特性和分形结构; 2)扣除混沌成分后的时间序列周期与原始ΔLOD时间序列的周期完全相同; 3)原始ΔLOD时间序列和其扣除趋势成分和周期成分后的时间序列的混沌特性无显著性差异, 但前者分形结构的复杂性相对更强.To study the nonlinear characteristics of changes in the Earth's rotation rate, a comprehensive analysis of the nonlinear characteristics of the length of day (ΔLOD) observations reflecting changes in the Earth’s rotation rate is conducted from multiple perspectives, including periodicity, chaos, and fractal, by using the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN), recursive quantitative analysis (RAQ), and Grassberger-Procaccia (GP) algorithms. The long-term high-accuracy ΔLOD observations from January 1, 1962 to December 31, 2023, were comprehensively and reliably analyzed and then used as dataset published by the International Earth Rotation and Reference Systems Service, IERS) 14C04 series. The present workfocuses on comparing and analyzing whether there are any significant differences in the ΔLOD characteristics before and after deducting the periodic or chaotic components of ΔLOD time series. The main conclusions obtained are as follows. 1) The ΔLOD time series consists of the well-known trend components, many periodic components, and chaotic components, and therefore can be characterized by obvious multi timescales, chaotic dynamics, and fractal structure. The characteristics were not considered in previous research. 2) The period of the ΔLOD time series after deducting the chaotic components is exactly the same as the period of the original ΔLOD time series, implying that the chaotic components have no effects on reconstruction nor analysis of the periodic components. 3) There is no significant difference in chaotic characteristics between the original ΔLOD time series and its time series after deducting trend and periodic components, but the complexity of the fractal structure of the former is relatively stronger. Not only can this work provide a valuable reference for studying the mechanism of changes in the Earth’s rotation rate, but also model such rotation changes and then predict the chances on different timescales.
-
Keywords:
- Earth’s rotation /
- period /
- chaos /
- fractal
[1] Holme R, de Viron O 2013 Nature 499 202
Google Scholar
[2] Buffett B, Knezek N, Holme R 2016 Geophys. J. Int. 204 1789
Google Scholar
[3] Meyrath T, van Dam T 2016 J. Geodyn. 99 1
Google Scholar
[4] Milyukov V, Mironov A, Kravchuk V, Amoruso A, Crescentini L 2013 J. Geodyn. 67 97
Google Scholar
[5] Duan P S, Liu G Y, Liu L T, Hu X G, Hao X G, Huang Y, Zhang Z M, Wang B B 2015 Earth, Planets Space 67 161
Google Scholar
[6] An Y C, Ding H, Chen Z F, Shen W B, Jiang W P 2023 Nat. Commun. 14 8130
Google Scholar
[7] Wolfgang R D, Daniela Thaller 2023 IERS Annual Report 2019 (Central Bureau. Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie) pp1233–127
[8] Bizouard C, Lambert S, Gattano C, Becker O, Richard J Y 2019 J. Geod. 93 621
Google Scholar
[9] Ray R D, Erofeeva S Y 2013 J. Geophys. Res. Solid Earth 119 1498
Google Scholar
[10] Dill R, Dobslaw H 2019 Geophys. J. Int. 218 801
Google Scholar
[11] Chen J L, Wilson C R, Kuang W J, Chao B F 2019 J. Geophys. Res. Solid Earth 124 13404
Google Scholar
[12] Yu N, Ray J, Li J C, Chen G, Chao N F, Chen W 2021 Earth Space Sci. 8 1563
Google Scholar
[13] Chao B F, Chung W Y, Shih Z R, Hsieh Y 2014 Terra Nova 26 260
Google Scholar
[14] Shen W B, Peng C C 2016 Geod. Geodyn. 7 180
Google Scholar
[15] Ding H 2019 Earth Planet. Sci. Lett. 507 131
Google Scholar
[16] Duan P S, Huang C L 2020 Nat. Commun. 11 2273
Google Scholar
[17] Ding H, Chao B F 2018 J. Geophys. Res. Solid Earth 123 8249
Google Scholar
[18] Ogunjo S, Rabiu B, Fuwape I, Atikekeresola O 2024 Adv. Space Res. 73 5406
Google Scholar
[19] Bolzan M J A, Paula K S S 2023 Adv. Space Res. 71 5114
Google Scholar
[20] David V, Galtier S, Meyrand R 2024 Phys. Rev. Lett. 132 85201
Google Scholar
[21] 周双, 冯勇, 吴文渊 2015 64 130504
Google Scholar
Zhou S, Fen Y, Wu W Y 2015 Acta Phys. Sin. 64 130504
Google Scholar
[22] Charles L, Marwan N 2015 Recurrence Quantification Analysis: Theory and Best Practices (New York: Springer) pp43–45
[23] Falconer K 2013 Fractals: A Very Short Introduction (New York: Oxford University Press) pp35–36
[24] Fernández-Martínez M, Sánchez-Granero M Á 2014 Topol. Appl. 163 93
Google Scholar
[25] Leonov G A, Florinskii A A 2019 Vestnik St Petersburg Univ. Math. 52 327
Google Scholar
[26] Rosenberg E 2020 Fractal Dimensions of Networks (New York: Springer) pp177–179
[27] Yeh J R, Shieh J S, Huang N E 2010 Adv. Adapt. Data Anal. , Theor. Appl. 2 135
Google Scholar
[28] Oppenheim A V, Schafer R W 2009 Discrete-Time Signal Processing (Upper Saddle River: Prentice Hall Press) pp53–60
[29] Eckmann J P, Kamphorst S O, Ruelle D 1987 Europhys. Lett. 4 973
Google Scholar
[30] Grassberger P, Procaccia 1983 Physica D 9 189
Google Scholar
[31] 师思, 周永宏, 许雪晴 2017 天文学进展 39 448
Google Scholar
Shi S, Zhou Y H, Xu X Q 2017 Prog. Astron. 39 448
Google Scholar
[32] Wang C J, Li H Y, Zhao D 2018 Circuits Syst. Signal Process. 37 5417
Google Scholar
[33] 许雪晴, 董大南, 周永宏 2014 天文学进展 32 338
Google Scholar
Xu X Q, Dong D N, Zhou Y H 2014 Prog. Astron. 32 338
Google Scholar
[34] Ding H, Li J C, Jiang W P, Shen W B 2024 Chin. Sci. Bull. 69 2038
Google Scholar
-
图 1 IERS EOP 14 C04发布的1962—2023年ΔLOD序列
Fig. 1. ΔLOD time series from 1962 to 2023 published by the IERS EOP 14 C04.
图 3 不同信号的递归图 (a) 随机信号; (b) 混沌信号; (c) 周期信号
Fig. 3. Signals recurrence plot of different signals: (a) Stochastic signals; (b) chaotic signals; (c) periodic signals.
图 4 GP算法估计关联维流程
Fig. 4. Flowchart of the GP algorithm for estimating correlation dimensions.
图 5 1962—2023年ΔLOD的IMF分量与趋势项 (a)—(i) IMF1—IMF9; (j) 趋势项
Fig. 5. IMF components and trend of the ΔLOD time-series from 1962 to 2023: (a)–(i) IMF1–IMF9; (j) trend.
图 6 IMF分量的频谱 (a)—(i) IMF1 —IMF9
Fig. 6. Frequency spectrum of the IMF components: (a)–(i) IMF1–IMF9.
图 7 扣除 IMF3分量的ΔLOD的频谱
Fig. 7. Frequency spectrum of the ΔLOD time series with the IMF3 component removed.
图 8 ΔLOD及其扣除趋势项和周期项的残差项的递归图 (a)—(d) ΔLOD的递归图; (e)—(h) ΔLOD残差 (IMF3分量)的递归图
Fig. 8. Recurrence plot of the ΔLOD and residual time series after the trend and periodic components removed: (a)–(d) Recurrence plot of the ΔLOD; (e)–(h) recurrence plot of the ΔLOD residuals (IMF3).
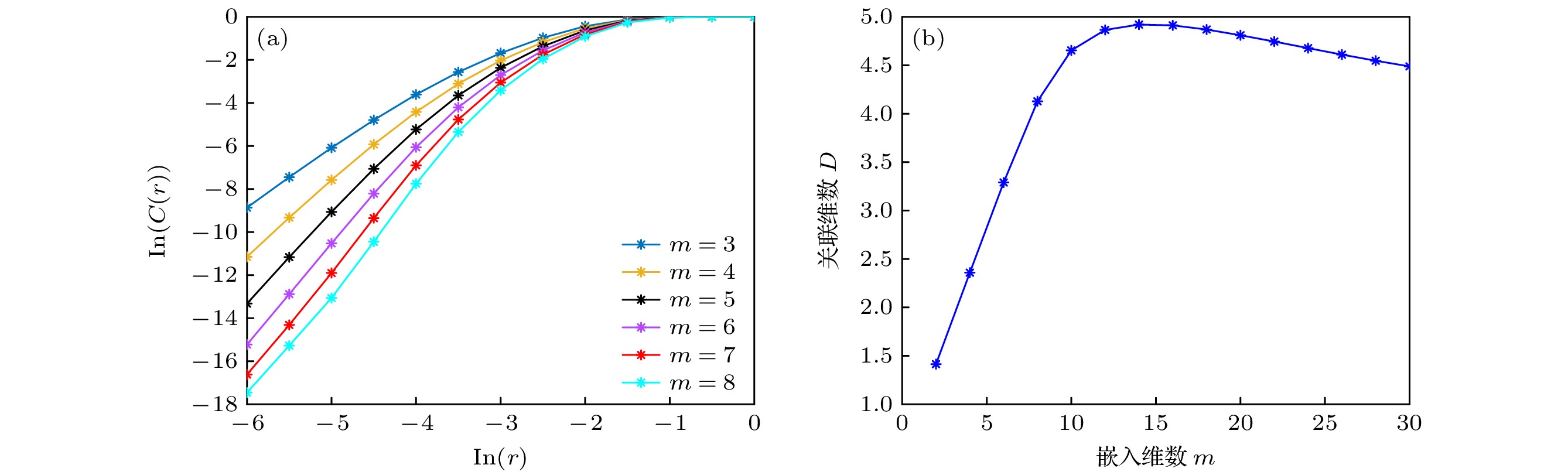
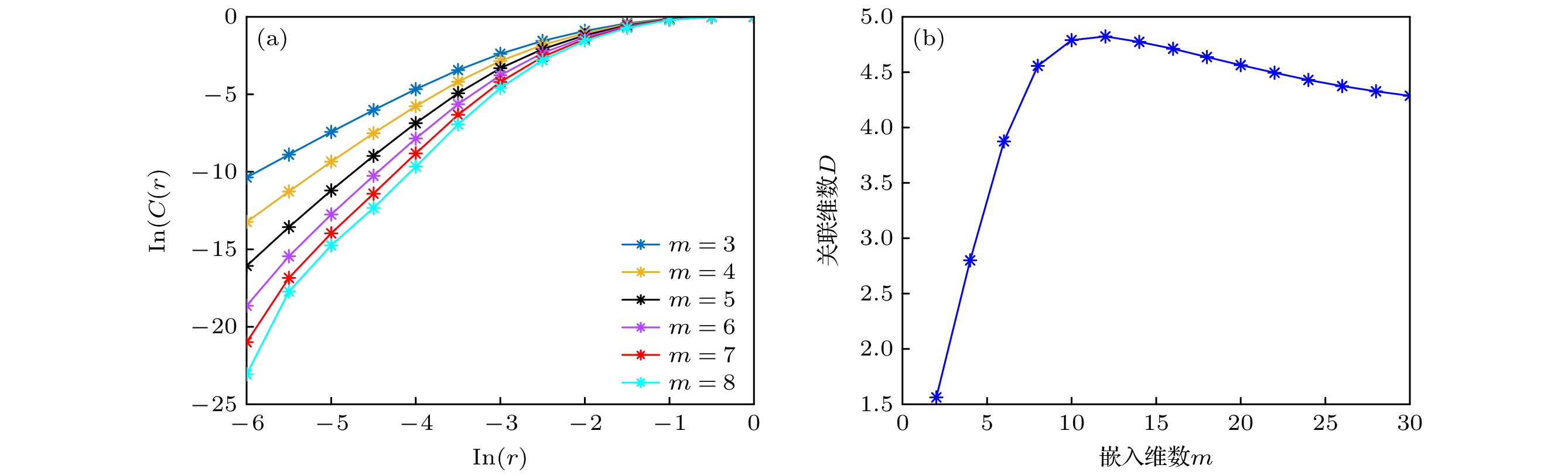
图 9 ΔLOD序列的关联维与嵌入维数之间的关系 (a) $ {\text{In}}\lambda $与$ {\text{In}}C\left( \lambda \right) $的关系; (b) 关联维D与嵌入维数m的关系
Fig. 9. Relationship between the correlation and embedding dimensions of the ΔLOD time series: (a) Relationship between $ {\text{In}}\lambda $ and $ {\text{In}}C\left( \lambda \right) $; (b) relationship between correlation and embedding dimensions.
图 10 ΔLOD残差项的关联维与嵌入维数之间的关系
Fig. 10. Relationship between the correlation and embedding dimensions of the ΔLOD residuals.
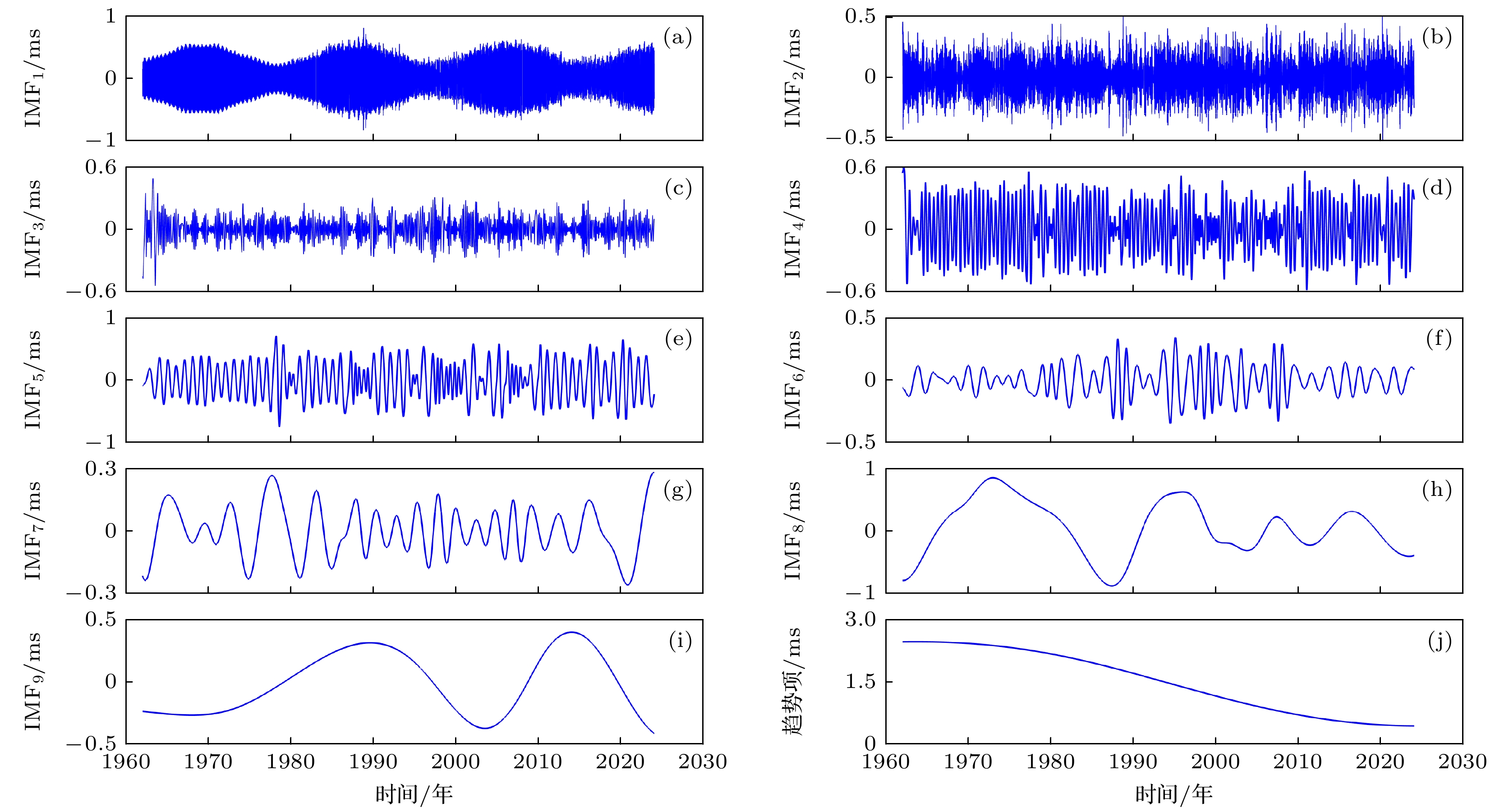
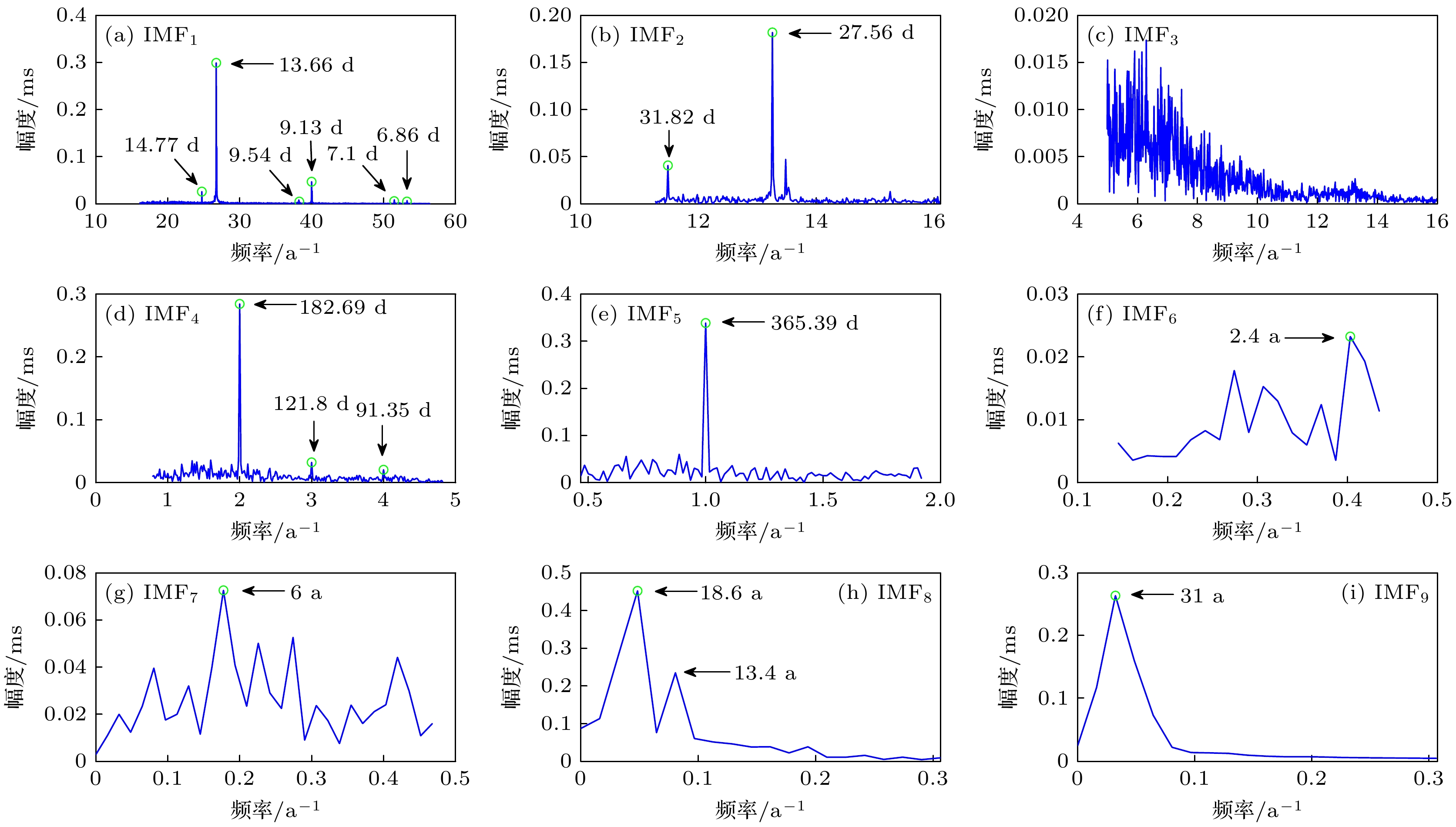
表 1 各IMF分量的方差贡献率
Table 1. Variance contribution rate of each IMF component.
模态分量 方差贡献率/% 模态分量 方差贡献率/% IMF1 10.43 IMF6 4.45 IMF2 6.03 IMF7 4.29 IMF3 3.85 IMF8 15.73 IMF4 8.93 IMF9 8.72 IMF5 10.66 趋势分量 26.91 
下载: 导出CSV
-
[1] Holme R, de Viron O 2013 Nature 499 202
Google Scholar
[2] Buffett B, Knezek N, Holme R 2016 Geophys. J. Int. 204 1789
Google Scholar
[3] Meyrath T, van Dam T 2016 J. Geodyn. 99 1
Google Scholar
[4] Milyukov V, Mironov A, Kravchuk V, Amoruso A, Crescentini L 2013 J. Geodyn. 67 97
Google Scholar
[5] Duan P S, Liu G Y, Liu L T, Hu X G, Hao X G, Huang Y, Zhang Z M, Wang B B 2015 Earth, Planets Space 67 161
Google Scholar
[6] An Y C, Ding H, Chen Z F, Shen W B, Jiang W P 2023 Nat. Commun. 14 8130
Google Scholar
[7] Wolfgang R D, Daniela Thaller 2023 IERS Annual Report 2019 (Central Bureau. Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie) pp1233–127
[8] Bizouard C, Lambert S, Gattano C, Becker O, Richard J Y 2019 J. Geod. 93 621
Google Scholar
[9] Ray R D, Erofeeva S Y 2013 J. Geophys. Res. Solid Earth 119 1498
Google Scholar
[10] Dill R, Dobslaw H 2019 Geophys. J. Int. 218 801
Google Scholar
[11] Chen J L, Wilson C R, Kuang W J, Chao B F 2019 J. Geophys. Res. Solid Earth 124 13404
Google Scholar
[12] Yu N, Ray J, Li J C, Chen G, Chao N F, Chen W 2021 Earth Space Sci. 8 1563
Google Scholar
[13] Chao B F, Chung W Y, Shih Z R, Hsieh Y 2014 Terra Nova 26 260
Google Scholar
[14] Shen W B, Peng C C 2016 Geod. Geodyn. 7 180
Google Scholar
[15] Ding H 2019 Earth Planet. Sci. Lett. 507 131
Google Scholar
[16] Duan P S, Huang C L 2020 Nat. Commun. 11 2273
Google Scholar
[17] Ding H, Chao B F 2018 J. Geophys. Res. Solid Earth 123 8249
Google Scholar
[18] Ogunjo S, Rabiu B, Fuwape I, Atikekeresola O 2024 Adv. Space Res. 73 5406
Google Scholar
[19] Bolzan M J A, Paula K S S 2023 Adv. Space Res. 71 5114
Google Scholar
[20] David V, Galtier S, Meyrand R 2024 Phys. Rev. Lett. 132 85201
Google Scholar
[21] 周双, 冯勇, 吴文渊 2015 64 130504
Google Scholar
Zhou S, Fen Y, Wu W Y 2015 Acta Phys. Sin. 64 130504
Google Scholar
[22] Charles L, Marwan N 2015 Recurrence Quantification Analysis: Theory and Best Practices (New York: Springer) pp43–45
[23] Falconer K 2013 Fractals: A Very Short Introduction (New York: Oxford University Press) pp35–36
[24] Fernández-Martínez M, Sánchez-Granero M Á 2014 Topol. Appl. 163 93
Google Scholar
[25] Leonov G A, Florinskii A A 2019 Vestnik St Petersburg Univ. Math. 52 327
Google Scholar
[26] Rosenberg E 2020 Fractal Dimensions of Networks (New York: Springer) pp177–179
[27] Yeh J R, Shieh J S, Huang N E 2010 Adv. Adapt. Data Anal. , Theor. Appl. 2 135
Google Scholar
[28] Oppenheim A V, Schafer R W 2009 Discrete-Time Signal Processing (Upper Saddle River: Prentice Hall Press) pp53–60
[29] Eckmann J P, Kamphorst S O, Ruelle D 1987 Europhys. Lett. 4 973
Google Scholar
[30] Grassberger P, Procaccia 1983 Physica D 9 189
Google Scholar
[31] 师思, 周永宏, 许雪晴 2017 天文学进展 39 448
Google Scholar
Shi S, Zhou Y H, Xu X Q 2017 Prog. Astron. 39 448
Google Scholar
[32] Wang C J, Li H Y, Zhao D 2018 Circuits Syst. Signal Process. 37 5417
Google Scholar
[33] 许雪晴, 董大南, 周永宏 2014 天文学进展 32 338
Google Scholar
Xu X Q, Dong D N, Zhou Y H 2014 Prog. Astron. 32 338
Google Scholar
[34] Ding H, Li J C, Jiang W P, Shen W B 2024 Chin. Sci. Bull. 69 2038
Google Scholar
下载:
计量
- 文章访问数: 694
- PDF下载量: 31
- 被引次数: 0
