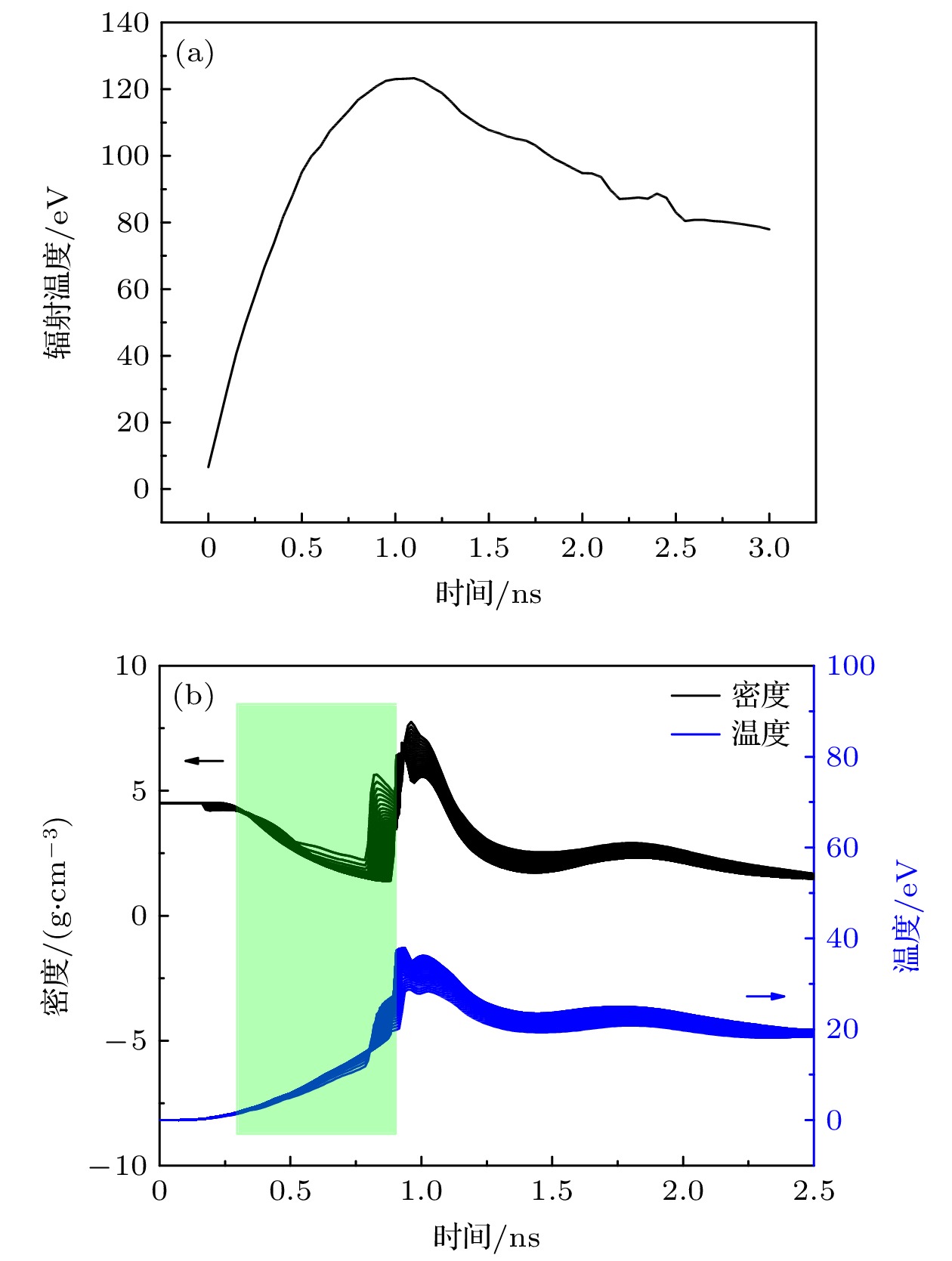
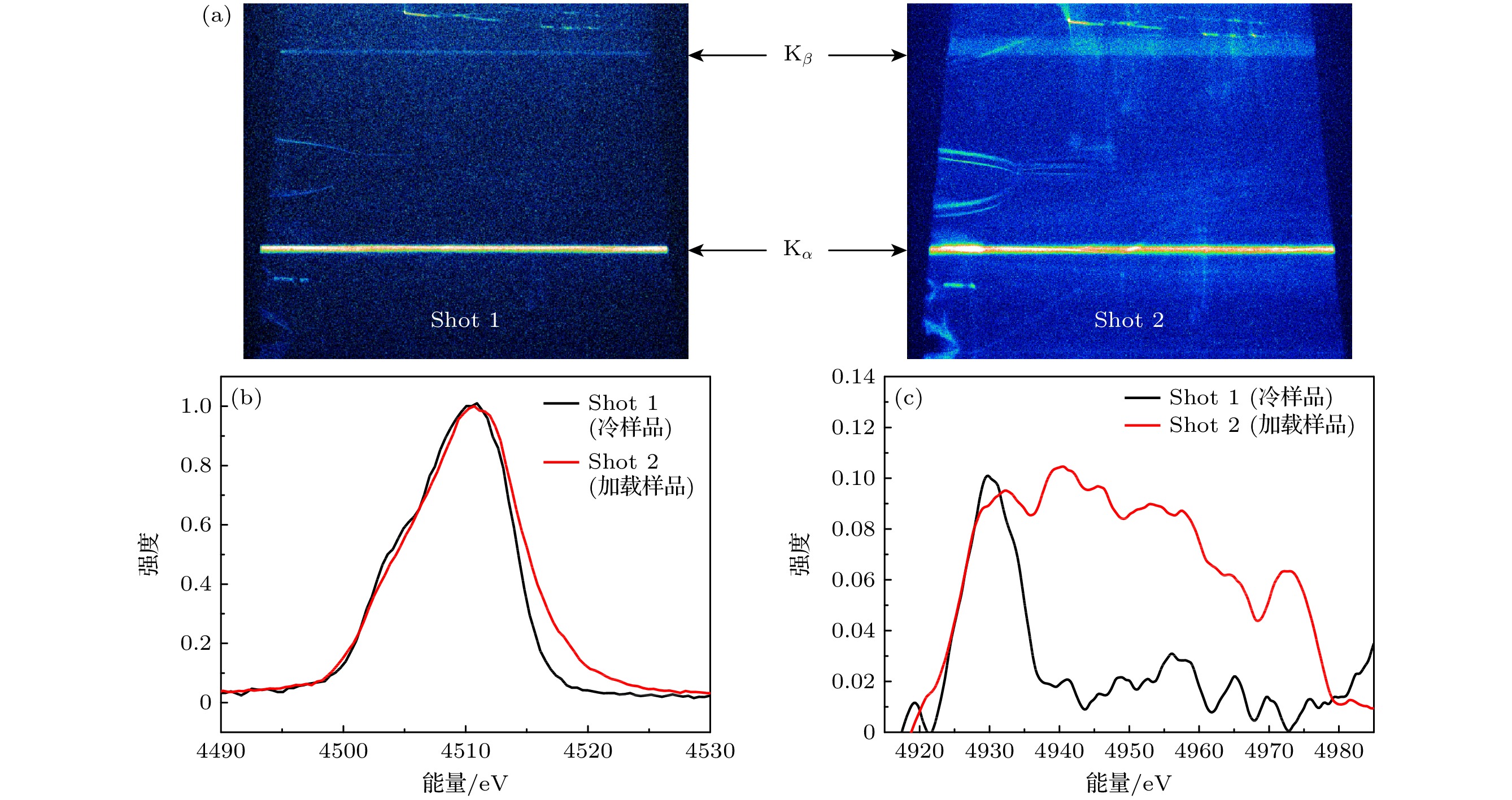
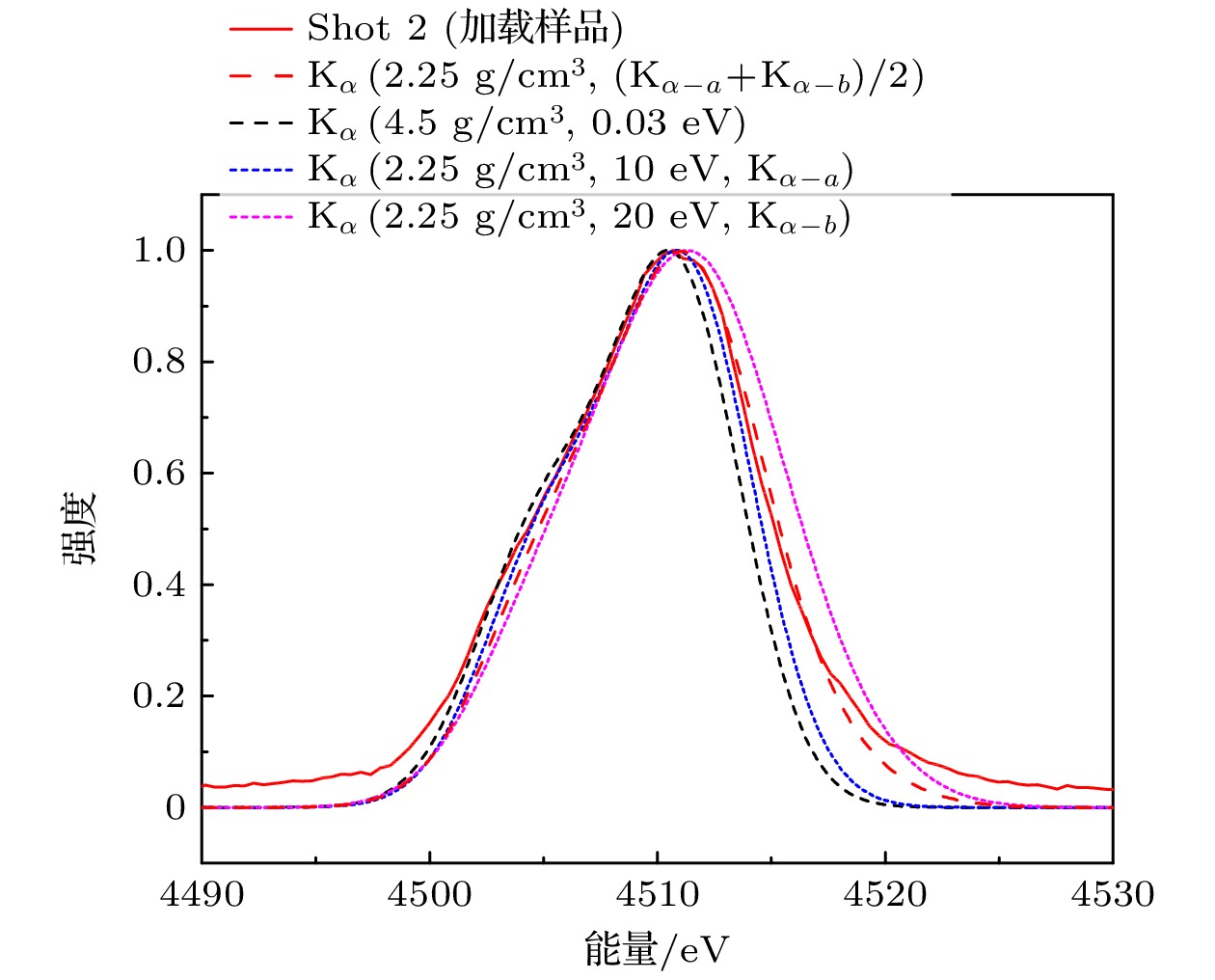
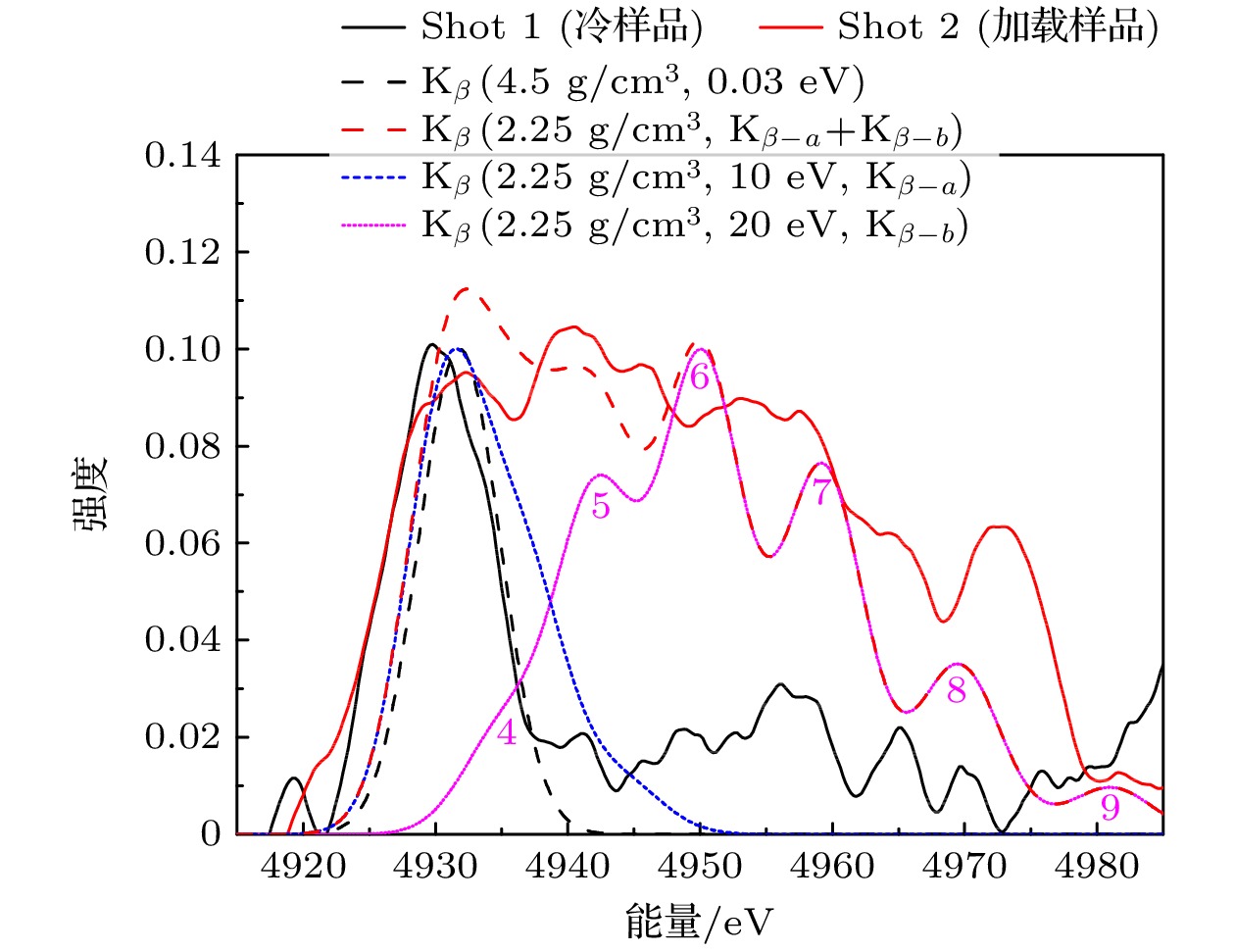
-
受温度及密度等环境效应影响, 温稠密物质的电子结构发生显著变化, 其理论描述非常复杂, 精密实验测量亦极其困难. 本文发展了基于X射线荧光光谱研究温稠密物质离化分布的实验方法, 结合理论研究有助于深入理解温稠密物质的电子结构变化. 在万焦耳激光装置上, 设计特殊构型黑腔复合加载产生数十eV、近固体密度的稠密Ti物质, 利用激光辐照V产生的热发射线泵浦Ti的荧光, 并采用晶体谱仪诊断样品的X射线荧光光谱. 实验中获得冷样品和加载样品的荧光光谱, 观测到加载样品Kα及Kβ荧光谱线相对于冷样品光谱在高能侧的显著变化, 结合理论计算解释了加载样品荧光谱线的变化主要来源于其温度上升后离化分布的改变, 建立了基于X射线荧光光谱的温稠密物质离化分布实验研究能力.Warm dense matter (WDM), a state of matter that lies at the frontier between condensed matter and plasma, is one of the main research objects of high energy density physics (HEDP). Comparing with the isolated atom, the electron structure of WDM will change because of the influence of density and temperature effect. Both the accurate theoretical representation and the accurate experimental study of WDM electron structure are challenging, as it is strongly coupled and partially degenerated. In this work, an experimental method of studying the ionization distribution of WDM based on X-ray fluorescence spectroscopy is developed. In the experiment, in a specially designed hohlraum, warm and dense titanium with several tens of electron volts and nearly solid density is produced by simultaneous driving of high-energy X-ray heating and shock compression. Then, using the characteristic line spectrum emitted by the laser irradiation on pump material (Vanadium) as a pump source, the titanium emits fluorescence. The X-ray fluorescence spectra of titanium with different states (cold sample, 1.8–4.5 g/cm3 and 1–25 eV) are diagnosed by changing the experimental strategy. The experimental results indicate that the line profiles of Kα and Kβ fluorescence spectrum of the heated sample change obviously compared with those of the cold sample. According to the theoretical calculation of the two-step Hartree-Fock-Slater (TSHFS) method, the main reason for the change of the line profile is the change of ionization distribution caused by temperature rising. The future work will focus on optimizing the experimental method of X-ray fluorescence spectrum, such as improving the spectrum resolution, characterizing the temperature and density experimentally, obtaining a set of ionization distribution data, and then studying the influence of dense environment on electronic structure.
-
Keywords:
- warm dense matter /
- electron structure /
- ionization distribution /
- X-ray fluorescence spectrum
[1] Saumon D, Chabrier G 1991 Phys. Rev. A 44 5122
Google Scholar
[2] Lindl J D 1995 Phys. Plasmas 2 3933
Google Scholar
[3] Surh M P, Barbee T W, Yang L H 2001 Phys. Rev. Lett. 86 5958
Google Scholar
[4] Mazevet S, Zérah G 2008 Phys. Rev. Lett. 101 155001
Google Scholar
[5] 金阳, 张平, 李永军, 侯永, 曾交龙, 袁建民 2021 70 073102
Google Scholar
Jin Y, Zhang P, Li Y J, Hou Y, Zeng J L, Yuan J M 2021 Acta Phys. Sin. 70 073102
Google Scholar
[6] Zhang S, Zhao S J, Kang W, Zhang P, He X T 2016 Phys. Rev. B 93 115114
Google Scholar
[7] Dai J Y, Hou Y, Yuan J M 2010 Phys. Rev. Lett. 104 245001
Google Scholar
[8] Wang C, He X T, Zhang P 2011 Phys. Rev. Lett. 106 145002
Google Scholar
[9] Bradley D K, Kilkenny J, Rose S J, Hares J D 1987 Phys. Rev. Lett. 59 2995
Google Scholar
[10] DaSilva L, Ng A, Godwal B K, Chiu G, Cottet F, Richardson M C, Jaanimagi P A, Lee Y T 1989 Phys. Rev. Lett. 62 1623
Google Scholar
[11] Yaakobi B, Boehly T R, Sangster T C, Meyerhofer D D, Remington B A, Allen P G, Pollaine S M, Lorenzana H E, Lorenz K T, Hawreliak J A 2008 Phys. Plasmas 15 062703
Google Scholar
[12] Benuzzi-Mounaix A, Dorchies F, Recoules V, Festa F, Peyrusse O, Levy A, Ravasio A, Hall T, Koenig M, Amadou N, Brambrink E, Mazevet S 2011 Phys. Rev. Lett. 107 165006
Google Scholar
[13] Zhao Y, Yang J M, Zhang J Y, Yang G H, Wei M X, Xiong G, Song T M, Zhang Z Y, Bao L H, Deng B, Li Y K, He X A, Li C G, Mei Y, Yu R Z, Jiang S E, Liu S Y, Ding Y K, Zhang B H 2013 Phys. Rev. Lett. 111 155003
Google Scholar
[14] Zhao Y, Zhang Z Y, Qing B, Yang J M, Zhang J Y, Wei M X, Yang G H, Song T M, Xiong G, Lü M, Hu Z M, Deng B, Hu X, Zhang W H, Shang W L, Hou L F, Du H B, Zhan X Y, Yu R Z 2017 EPL 117 65001
Google Scholar
[15] Hansen S B, Harding E C, Knapp P F, Gomez M R, Nagayama T, Bailey J E 2017 High Energy Density Phys. 24 39
Google Scholar
[16] Hansen S B, Harding E C, Knapp P F, Gomez M R, Nagayama T, Bailey J E 2018 Phys. Plasmas 25 056301
Google Scholar
[17] Jiang S, Lazicki A E, Hansen S B, Sterne P A, Grabowski P, Shepherd R, Scott H A 2020 Phys. Rev. E 101 023204
Google Scholar
[18] Mančić A, Lévy A, Harmand M, Nakatsutsumi M, Antici P, Audebert P, Combis P, Fourmaux S, Mazevet S, Peyrusse O, Recoules V, Renaudin P, Robiche J, Dorchies F, Fuchs J 2010 Phys. Rev. Lett. 104 035002
Google Scholar
[19] Park H, Remington B A, Braun D, Celliers P, Collins G W, Eggert J, Giraldez E, Pape S L, Lorenz T, Maddox B, Hamza A, Ho D, Hicks D, Patel P, Pollaine S, Prisbrey S, Smith R, Swift D, Wallace R 2008 J. Phys. Conf. Ser. 112 042024
Google Scholar
[20] Lee H J, Neumayer P, Castor J, Döppner T, Falcone R W, Fortmann C, Hammel B A, Kritcher A L, Landen O L, Lee R W, Meyerhofer D D, Munro D H, Redmer R, Regan S P, Weber S, Glenzer S H 2009 Phys. Rev. Lett. 102 115001
Google Scholar
[21] Benuzzi-Mounaix A, Mazevet S, Ravasio A, Vinci T, Denoeud A, Koenig M, Amadou N, Brambrink E, Festa F, Levy A, Harmand M, Brygoo S, Huser G, Recoules V, Bouchet J, Morard G, Guyot F, Resseguier T, Myanishi K, Ozaki N, Dorchies F, Gaudin J, Leguay P M, Peyrusse O, Henry O, Raffestin D, Pape S, Smith R, Musella R 2014 Phys. Scr. T161 014060
Google Scholar
[22] Zhang Z Y, Zhao Y, Zhang J Y, Hu Z M, Jing L F, Qing B, Xiong G, Lü M, Du H B, Yang Y M, Zhan X Y, Yu R Z, Mei Y, Yang J M 2019 Phys. Plasmas 26 072704
Google Scholar
[23] Eidmann K, Andiel U, Pisani F, Hakel P, Mancini R C, Junkel-Vives G C, Abdallah J, Witte K 2003 J. Quant. Spectrosc. Radiat. Transfer 81 133
Google Scholar
[24] Ramis R, Schmalz R, Meyer-Ter-Vehn J 1988 Comput. Phys. Commun. 49 475
Google Scholar
[25] Son S K, Thiele R, Jurek Z, Ziaja B, Santra R 2014 Phys. Rev. X 4 031004
Google Scholar
[26] Lin C L 2019 Phys. Plasmas 26 122707
Google Scholar
-
图 1 温稠密Ti的荧光光谱实验示意图 (a)荧光光谱测量; (b)样品处辐射源测量
Fig. 1. Schematic of the X-ray fluorescence spectrum experiment of warm dense Ti: (a) Measurement of the X-ray fluorescence spectrum; (b) measurement of the radiation source for sample
图 2 (a)样品处辐射源; (b) Ti样品的温度密度演化过程模拟结果, 绿色区域对应Shot 2的诊断时间窗口
Fig. 2. (a) Incident flux for the sample; (b) simulated density and temperature evolution of Ti sample, and the green area corresponds to the diagnostic window for Shot 2
图 3 不同状态Ti样品的荧光光谱 (a)原始图像; (b) $ {\mathrm{K}}_{\alpha} $解谱结果; (c) $ {\mathrm{K}}_{\beta} $解谱结果
Fig. 3. X-ray fluorescence spectrum of Ti samples with different state: (a) Original images; (b) spectral results of $ {\mathrm{K}}_{\alpha} $; (c) spectral results of $ {\mathrm{K}}_{\beta} $
图 4 冷Ti样品$ {\mathrm{K}}_{\alpha} $计算结果与实验结果的比较
Fig. 4. Comparison between simulated results and experimental results of cold Ti sample $ {\mathrm{K}}_{\alpha}$
图 5 加载Ti样品$ {\mathrm{K}}_\alpha $荧光光谱计算结果与实验结果的对比
Fig. 5. Comparison between simulated results and experimental results of warm dense Ti sample $ {\mathrm{K}}_\alpha $
图 6 Ti样品$ {\mathrm{K}}_{\beta} $计算结果与实验结果的比较, 图中数字代表Ti的价态
Fig. 6. Comparison between simulated results and experimental results of Ti sample $ {\mathrm{K}}_{\beta}$, the numbers in the figure represent the valence state of Ti
表 1 密度为2.25 $ {\mathrm{g/cm}}^3 $、不同温度Ti的离化分布的相应荧光谱线能量
Table 1. Ionization distribution and spectrum line energy of Ti with 2.25 $ {\mathrm{g/cm}}^3 $ and different temperature
温度/eV 价态 组态 组态占比率 $ {\mathrm{K}}_{\alpha1} $能量/eV $ {\mathrm{K}}_{\beta} $能量/eV 10 4 $ 1 {\mathrm{s}}^22 {\mathrm{s}}^22 {\mathrm{p}}^63 {\mathrm{s}}^23 {\mathrm{p}}^6 $ 0.59 4510.78 4930.90 5 $ 1 {\mathrm{s}}^22 {\mathrm{s}}^22 {\mathrm{p}}^63 {\mathrm{s}}^23 {\mathrm{p}}^5 $ 0.31 4511.95 4936.91 5 $ 1 {\mathrm{s}}^22 {\mathrm{s}}^22 {\mathrm{p}}^63 {\mathrm{s}}^13 {\mathrm{p}}^6 $ 0.01 4511.80 4936.99 6 $ 1 s^22 s^22 p^63 s^23 p^4 $ 0.07 4513.47 4944.08 20 4 $ 1{\mathrm{ s}}^22 {\mathrm{s}}^22 {\mathrm{p}}^63 {\mathrm{s}}^23{\mathrm{ p}}^6 $ 0.07 4508.75 4935.17 5 $ 1 {\mathrm{s}}^22 {\mathrm{s}}^22 {\mathrm{p}}^63 {\mathrm{s}}^23 {\mathrm{p}}^5 $ 0.20 4510.24 4942.15 5 $ 1 {\mathrm{s}}^22 {\mathrm{s}}^22 {\mathrm{p}}^63 {\mathrm{s}}^13 {\mathrm{p}}^6 $ 0.02 4510.01 4942.00 6 $ 1 {\mathrm{s}}^22 {\mathrm{s}}^22 {\mathrm{p}}^63 {\mathrm{s}}^23 {\mathrm{p}}^4 $ 0.25 4512.07 4950.23 6 $ 1 {\mathrm{s}}^22 {\mathrm{s}}^22 {\mathrm{p}}^63 {\mathrm{s}}^13 {\mathrm{p}}^5 $ 0.06 4511.80 4949.96 7 $ 1 {\mathrm{s}}^22 {\mathrm{s}}^22 {\mathrm{p}}^63 {\mathrm{s}}^23 {\mathrm{p}}^3 $ 0.16 4514.26 4959.43 7 $ 1 {\mathrm{s}}^22{\mathrm{ s}}^22 {\mathrm{p}}^63 {\mathrm{s}}^13 {\mathrm{p}}^4 $ 0.08 4513.95 4959.03 8 $ 1 {\mathrm{s}}^22 {\mathrm{s}}^22 {\mathrm{p}}^63 {\mathrm{s}}^23{\mathrm{ p}}^2 $ 0.06 4516.83 4969.80 8 $ 1 {\mathrm{s}}^22 {\mathrm{s}}^22 {\mathrm{p}}^63 {\mathrm{s}}^13 {\mathrm{p}}^3 $ 0.05 4516.47 4969.27 9 $ 1 {\mathrm{s}}^22 {\mathrm{s}}^22 {\mathrm{p}}^63 {\mathrm{s}}^23{\mathrm{ p}}^1 $ 0.01 4519.78 4981.40 9 $ 1 {\mathrm{s}}^22{\mathrm{ s}}^22 {\mathrm{p}}^63 {\mathrm{s}}^13{\mathrm{ p}}^2 $ 0.02 4519.38 4980.74 注: 组态占比率小于0.01的组态已忽略 
下载: 导出CSV
-
[1] Saumon D, Chabrier G 1991 Phys. Rev. A 44 5122
Google Scholar
[2] Lindl J D 1995 Phys. Plasmas 2 3933
Google Scholar
[3] Surh M P, Barbee T W, Yang L H 2001 Phys. Rev. Lett. 86 5958
Google Scholar
[4] Mazevet S, Zérah G 2008 Phys. Rev. Lett. 101 155001
Google Scholar
[5] 金阳, 张平, 李永军, 侯永, 曾交龙, 袁建民 2021 70 073102
Google Scholar
Jin Y, Zhang P, Li Y J, Hou Y, Zeng J L, Yuan J M 2021 Acta Phys. Sin. 70 073102
Google Scholar
[6] Zhang S, Zhao S J, Kang W, Zhang P, He X T 2016 Phys. Rev. B 93 115114
Google Scholar
[7] Dai J Y, Hou Y, Yuan J M 2010 Phys. Rev. Lett. 104 245001
Google Scholar
[8] Wang C, He X T, Zhang P 2011 Phys. Rev. Lett. 106 145002
Google Scholar
[9] Bradley D K, Kilkenny J, Rose S J, Hares J D 1987 Phys. Rev. Lett. 59 2995
Google Scholar
[10] DaSilva L, Ng A, Godwal B K, Chiu G, Cottet F, Richardson M C, Jaanimagi P A, Lee Y T 1989 Phys. Rev. Lett. 62 1623
Google Scholar
[11] Yaakobi B, Boehly T R, Sangster T C, Meyerhofer D D, Remington B A, Allen P G, Pollaine S M, Lorenzana H E, Lorenz K T, Hawreliak J A 2008 Phys. Plasmas 15 062703
Google Scholar
[12] Benuzzi-Mounaix A, Dorchies F, Recoules V, Festa F, Peyrusse O, Levy A, Ravasio A, Hall T, Koenig M, Amadou N, Brambrink E, Mazevet S 2011 Phys. Rev. Lett. 107 165006
Google Scholar
[13] Zhao Y, Yang J M, Zhang J Y, Yang G H, Wei M X, Xiong G, Song T M, Zhang Z Y, Bao L H, Deng B, Li Y K, He X A, Li C G, Mei Y, Yu R Z, Jiang S E, Liu S Y, Ding Y K, Zhang B H 2013 Phys. Rev. Lett. 111 155003
Google Scholar
[14] Zhao Y, Zhang Z Y, Qing B, Yang J M, Zhang J Y, Wei M X, Yang G H, Song T M, Xiong G, Lü M, Hu Z M, Deng B, Hu X, Zhang W H, Shang W L, Hou L F, Du H B, Zhan X Y, Yu R Z 2017 EPL 117 65001
Google Scholar
[15] Hansen S B, Harding E C, Knapp P F, Gomez M R, Nagayama T, Bailey J E 2017 High Energy Density Phys. 24 39
Google Scholar
[16] Hansen S B, Harding E C, Knapp P F, Gomez M R, Nagayama T, Bailey J E 2018 Phys. Plasmas 25 056301
Google Scholar
[17] Jiang S, Lazicki A E, Hansen S B, Sterne P A, Grabowski P, Shepherd R, Scott H A 2020 Phys. Rev. E 101 023204
Google Scholar
[18] Mančić A, Lévy A, Harmand M, Nakatsutsumi M, Antici P, Audebert P, Combis P, Fourmaux S, Mazevet S, Peyrusse O, Recoules V, Renaudin P, Robiche J, Dorchies F, Fuchs J 2010 Phys. Rev. Lett. 104 035002
Google Scholar
[19] Park H, Remington B A, Braun D, Celliers P, Collins G W, Eggert J, Giraldez E, Pape S L, Lorenz T, Maddox B, Hamza A, Ho D, Hicks D, Patel P, Pollaine S, Prisbrey S, Smith R, Swift D, Wallace R 2008 J. Phys. Conf. Ser. 112 042024
Google Scholar
[20] Lee H J, Neumayer P, Castor J, Döppner T, Falcone R W, Fortmann C, Hammel B A, Kritcher A L, Landen O L, Lee R W, Meyerhofer D D, Munro D H, Redmer R, Regan S P, Weber S, Glenzer S H 2009 Phys. Rev. Lett. 102 115001
Google Scholar
[21] Benuzzi-Mounaix A, Mazevet S, Ravasio A, Vinci T, Denoeud A, Koenig M, Amadou N, Brambrink E, Festa F, Levy A, Harmand M, Brygoo S, Huser G, Recoules V, Bouchet J, Morard G, Guyot F, Resseguier T, Myanishi K, Ozaki N, Dorchies F, Gaudin J, Leguay P M, Peyrusse O, Henry O, Raffestin D, Pape S, Smith R, Musella R 2014 Phys. Scr. T161 014060
Google Scholar
[22] Zhang Z Y, Zhao Y, Zhang J Y, Hu Z M, Jing L F, Qing B, Xiong G, Lü M, Du H B, Yang Y M, Zhan X Y, Yu R Z, Mei Y, Yang J M 2019 Phys. Plasmas 26 072704
Google Scholar
[23] Eidmann K, Andiel U, Pisani F, Hakel P, Mancini R C, Junkel-Vives G C, Abdallah J, Witte K 2003 J. Quant. Spectrosc. Radiat. Transfer 81 133
Google Scholar
[24] Ramis R, Schmalz R, Meyer-Ter-Vehn J 1988 Comput. Phys. Commun. 49 475
Google Scholar
[25] Son S K, Thiele R, Jurek Z, Ziaja B, Santra R 2014 Phys. Rev. X 4 031004
Google Scholar
[26] Lin C L 2019 Phys. Plasmas 26 122707
Google Scholar
下载:
计量
- 文章访问数: 1825
- PDF下载量: 45
- 被引次数: 0
