-
时域有限差分方法(finite-difference time-domain, FDTD(2, 2))被广泛用于量子力学中薛定谔方程的求解, 然而受Courant-Friedrichs-Lewy (CFL)条件的影响, 计算空间中的网格尺寸会限制时间步长的取值范围, 极大降低了FDTD(2, 2)方法的数值计算效率. 另外, FDTD(2, 2)方法在时间域和空间域只具有二阶数值精度, 在计算中往往会导致较大的误差累计, 影响仿真结果的正确性. 为了克服这些问题, 结合空间滤波方法(spatial filtering, SF)和高阶辛时域有限差分 (symplectic finite-difference time-domain, SFDTD(3, 4))方法(3和4分别表示时间和空间数值精度), 提出了一种时间稳定性条件可扩展的SF-SFDTD(3, 4)方法用于求解含时薛定谔方程. SF-SFDTD(3, 4)方法无需对传统SFDTD(3, 4)方法的迭代公式进行进一步的推导, 只需要在每一次的数值迭代过程中加入空间滤波操作, 滤除因采用不满足CFL条件的时间步长而产生的不稳定空间域高频分量, 保证数值方法的稳定性, 因此所提方法与传统SFDTD(3, 4)方法具有较高的兼容性. 同时, 理论分析了SF-SFDTD(3, 4)方法的数值色散误差. 最后, 通过数值算例验证了本文所提方法的正确性和有效性.The traditional finite-difference time-domain (FDTD (2, 2)) method with second-order numerical accuracy in time and space has been extensively employed in the field of quantum mechanics to solve the Schrödinger equation. Nevertheless, the presence of the Courant-Friedrichs-Lewy (CFL) condition imposes limitations on the grid size in the computational space, thereby constraining the admissible range of time steps. Accordingly, the efficiency of the FDTD(2, 2) method significantly decreases. In addition, the second-order numerical accuracy of the FDTD(2, 2) method both in time domain and in space domain often results in significant error accumulation during calculations, thereby undermining the fidelity of the simulation results. To surmount the constraints imposed by the CFL stability conditions and enhance the accuracy of computations, a novel approach termed SF-SFDTD(3, 4) method has been proposed, with 3 and 4 referring to the accuracy in space and time, respectively. This method combines spatial filtering (SF) with the high-order symplectic finite-difference time-domain (SFDTD) method. Its primary objective is to solve the time-dependent Schrödinger equation while ensuring time stability and scalability. The SF-SFDTD(3, 4) method obviates the need for further deriving the iterative formula employed in the conventional SFDTD(3, 4) method. Therefore, the method under consideration exhibits a remarkable degree of compatibility with its traditional counterpart. It is merely necessary to include a spatial filtering operation during each numerical iteration to eliminate spatial high-frequency components arising from the utilization of time step sizes that fail to satisfy the CFL stability condition, thereby ensuring the stability of the numerical scheme. Moreover, when the time step value satisfies the CFL stability condition, the amplitude of the high-frequency component approaches zero, thereby exerting a minimal influence on the accuracy of the computational results. The adoption of time steps that do not meet the CFL stability conditions leads to an amplification in the amplitude of the high-frequency component. However, this finding solely affects the stability of the computational results, and the elimination of these unstable high-frequency components scarcely affect the accuracy of the computational results. The SF-SFDTD(3, 4) retains the simplicity and efficacy inherent in the traditional SFDTD(3, 4) methods, while enhancing computational efficiency. Additionally, the numerical stability and dispersion error of the SF-SFDTD(3, 4) method are analyzed theoretically. Finally, the validity and efficacy of the proposed method are corroborated through numerical illustrations.
-
Keywords:
- symplectic finite-difference time-domain method /
- spatial filtering /
- time stability condition /
- Schrödinger equation
[1] Jin J M 2010 Theory and Computational of Electromagnetic Fields (Hoboken, NJ, USA: Wiley
[2] Harrington R F 1968 Field Computation by Moment Methods (New York: Macmillan
[3] Feng B, Chen J, Chung K L, Wang L, Li Y 2022 IEEE Trans. Antennas Propag. 70 3058
Google Scholar
[4] Manoufali M, Mobashsher A T, Mohammed B, et al. 2020 IEEE Trans. Biomed. Circuits Sys. 14 452
Google Scholar
[5] Schwierz F 2010 Nat. Nanotechnol. 5 487
Google Scholar
[6] Russer P, Fichtner N, Lugli P, Porod W, Russer J A, Yordanov H 2010 IEEE Microwave Mag. 11 58
Google Scholar
[7] Datta S 2005 Quantum Transport: Atom to Transistor (New York: Cambridge University Press
[8] Joe Y S, Satanin A M, Kim C S 2006 Phys. Scr. 74 259
Google Scholar
[9] Griffiths D J 2004 Introduction to Quantum Mechanics (2nd Ed.) (Boston: Addison-Wesley
[10] Soriano A, Navarro E A, Portì J A, Such V 2004 J. Appl. Phys 95 8011
Google Scholar
[11] Sullivan D M, Citrin D S 2005 J. Appl. Phys. 97 104305
Google Scholar
[12] Zhu M, Wang Y 2020 2020 Cross Strait Radio Science & Wireless Technology Conference (CSRSWTC), Fuzhou, China, October 11–14, 2020 p1
[13] Decleer P, Van Londersele A, Rogier H, Vande Ginste D 2021 J. Comput. Appl. Math. 381 113023
Google Scholar
[14] 沈晶, 沙威, 黄志祥, 陈明生, 吴先良 2012 61 190202
Google Scholar
Shen J, Sha Wei E I, Huang Z X, Chen M S, Wu X L 2012 Acta Phys. Sin. 61 190202
Google Scholar
[15] Taflove A, Hagness S C 2005 Computational Electrodynamics: the Finite-Difference Time-Domain Method (3rd Ed.) (Boston: Artech House
[16] Sarris C D 2011 IEEE Microwave Wireless Compon. Lett. 21 176
Google Scholar
[17] Chang C, Sarris C D 2013 IEEE Trans. Microwave Theory Tech. 61 351
Google Scholar
[18] Gao Y J, Zhang J H, Yao Z X 2019 J. Comput. Phys. 397 108853
Google Scholar
[19] Decleer P 2018 M. S. Thesis (Ghent: Ghent University
[20] Cao Q, Chen Y, Mittra R 2002 IEEE Trans. Microwave Theory Tech. 50 1578
Google Scholar
-
图 1 kmax$\varDelta $ = 0.1π时, Q(θ, $\varphi $)随θ, $\varphi $的变化
Fig. 1. Variation of Q(θ, $\varphi $) with θ, $\varphi $ at kmax$\varDelta $ = 0.1π.
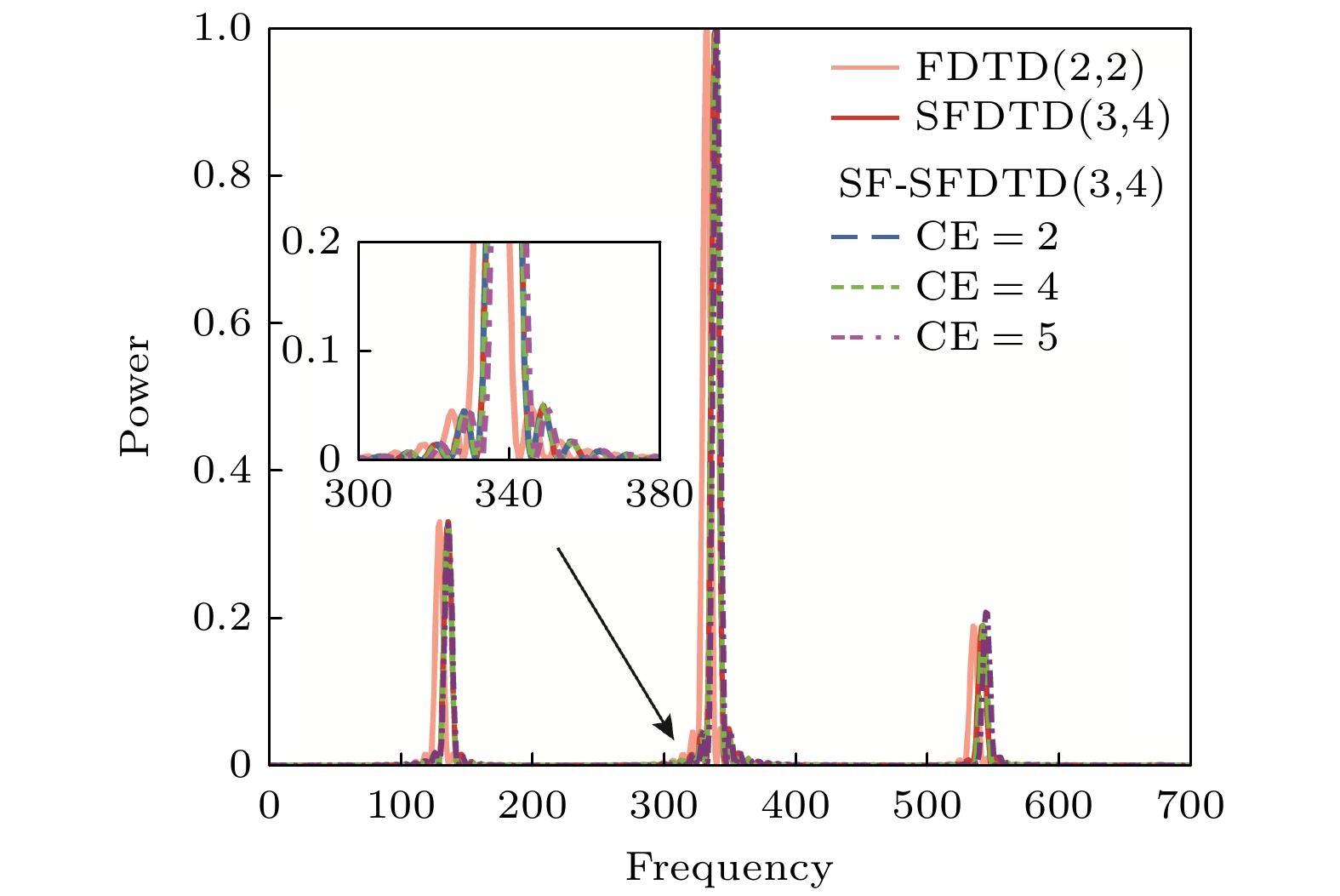
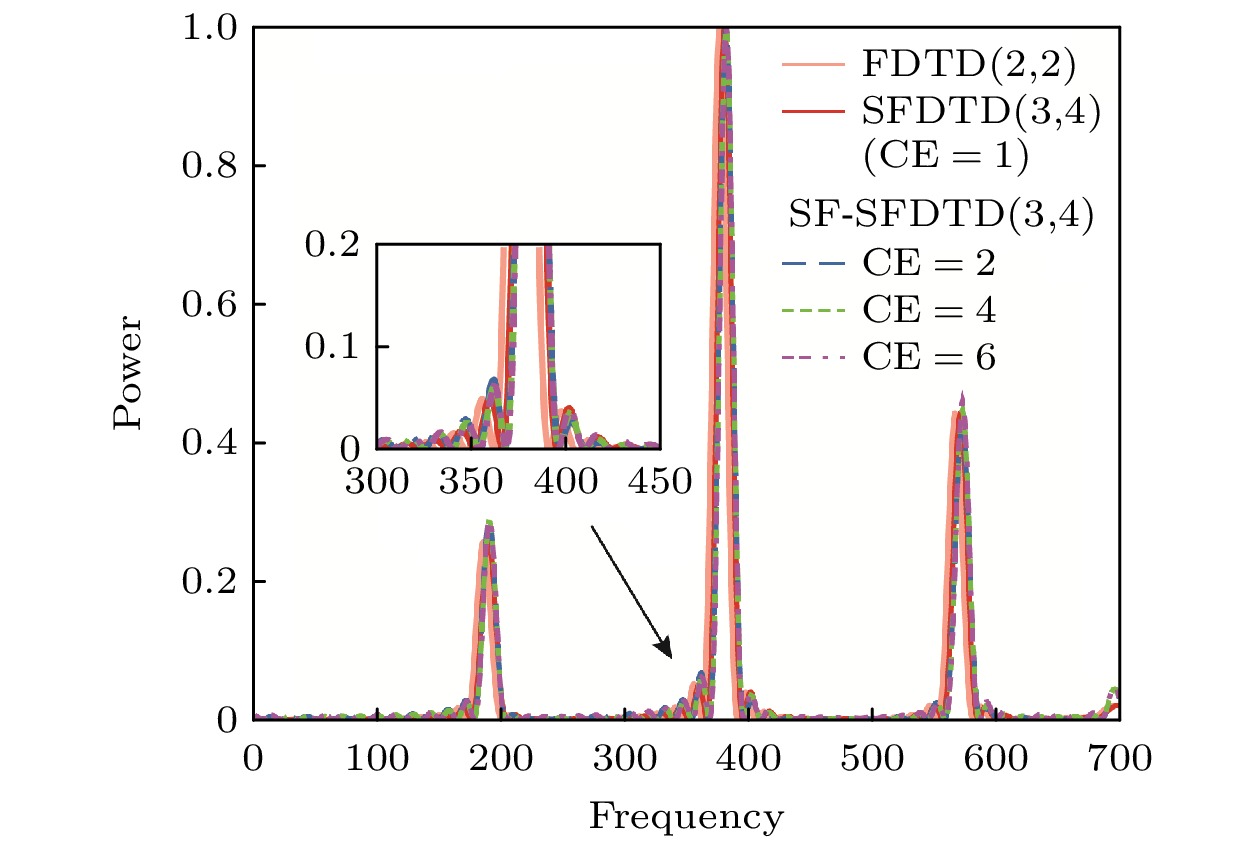
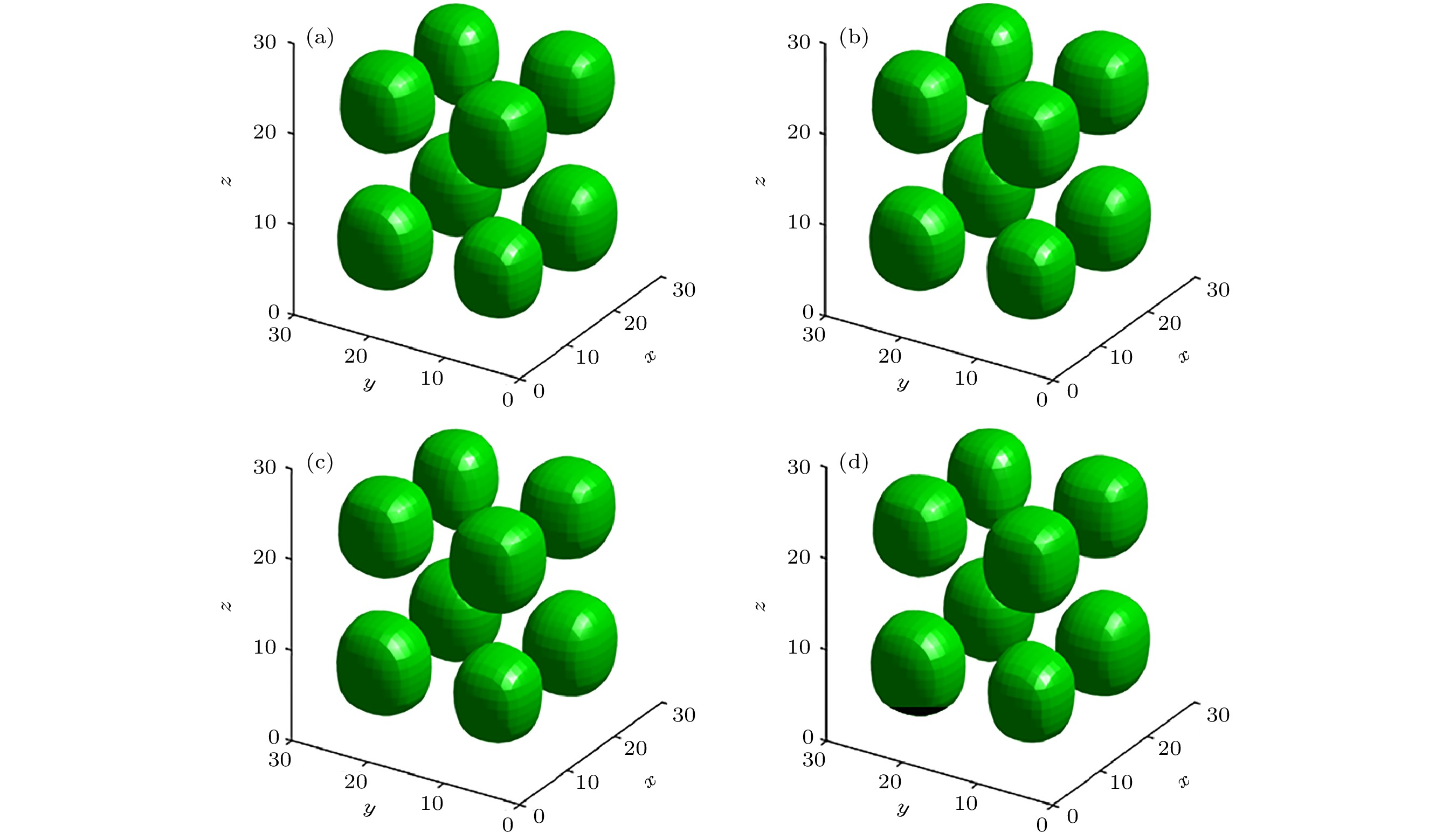
图 4 FDTD(2, 2), SFDTD(3, 4)和SF-SFDTD(3, 4)方法的数值色散误差 (a) FDTD(2, 2)(CE = 1); (b) SFDTD(3, 4)(CE = 1); (c) SF-SFDTD(3, 4)(CE = 5); (d) SF-SFDTD(3, 4)(CE = 10)
Fig. 4. Curves of numerical dispersion error for the FDTD(2, 2), SFDTD(3, 4) and SF-SFDTD(3, 4) method: (a) FDTD(2, 2)(CE = 1); (b) SFDTD(3, 4)(CE = 1); (c) SF-SFDTD(3, 4)(CE = 5); (d) SF-SFDTD(3, 4)(CE = 10).
图 5 二维薛定谔方程的特征频率
Fig. 5. Eigenfrequencies of the two-dimensional Schrödinger equation.
图 6 二维薛定谔方程在不同时间步长下的本征态(ψ2, 2) (a) CE = 1; (b) CE = 2; (c) CE = 4; (d) CE = 5
Fig. 6. Eigenstates of two-dimensional Schrödinger equation at different time steps (ψ2, 2): (a) CE = 1; (b) CE = 2; (c) CE = 4; (d) CE = 5.
图 7 三维薛定谔方程的特征频率
Fig. 7. Eigenfrequencies of the three-dimensional Schrödinger equation.
图 8 三维薛定谔方程在不同时间步下的本征态(ψ2, 2, 2) (a) CE = 1; (b) CE = 2; (c) CE = 4; (d) CE = 6
Fig. 8. Eigenstates of three -dimensional Schrödinger equation at different time steps (ψ2, 2, 2): (a) CE = 1; (b) CE = 2; (c) CE = 4; (d) CE = 6.
图 9 FDTD(2, 2), SFDTD(3, 4)和SF-SFDTD(3, 4)方法计算所得前四个特征频率点的相对计算误差
Fig. 9. Relative calculation errors of the first four characteristic frequency points were calculated by FDTD(2, 2), SFDTD(3, 4) and SF-SFDTD(3, 4) methods.
表 1 SFDTD(3, 4)和SF-SFDTD(3, 4)方法数值求解二维薛定谔方程的运行时间
Table 1. Execution time(s) for SFDTD(3, 4) and SF-SFDTD(3, 4) methods for solving two-dimensional Schrödinger equation.
计算方法 CE 迭代步数 运行时间/s SFDTD(3, 4) 1 40000 7.78 SF-SFDTD(3, 4) 2 20000 16.18 SF-SFDTD(3, 4) 4 10000 7.98 SF-SFDTD(3, 4) 5 8000 4.51 
下载: 导出CSV
表 2 SFDTD(3, 4)和SF-SFDTD(3, 4)方法数值求解三维薛定谔方程的运行时间的运行时间
Table 2. Execution time(s) for SFDTD(3, 4) and SF-SFDTD(3, 4) methods for solving three-dimensional Schrödinger equation.
计算方法 CE 迭代次数 运行时间/s SFDTD(3, 4) 1 30000 117.37 SF-SFDTD(3, 4) 2 15000 231.15 SF-SFDTD(3, 4) 4 7500 121.20 SF-SFDTD(3, 4) 6 5000 79.40
下载: 导出CSV
-
[1] Jin J M 2010 Theory and Computational of Electromagnetic Fields (Hoboken, NJ, USA: Wiley
[2] Harrington R F 1968 Field Computation by Moment Methods (New York: Macmillan
[3] Feng B, Chen J, Chung K L, Wang L, Li Y 2022 IEEE Trans. Antennas Propag. 70 3058
Google Scholar
[4] Manoufali M, Mobashsher A T, Mohammed B, et al. 2020 IEEE Trans. Biomed. Circuits Sys. 14 452
Google Scholar
[5] Schwierz F 2010 Nat. Nanotechnol. 5 487
Google Scholar
[6] Russer P, Fichtner N, Lugli P, Porod W, Russer J A, Yordanov H 2010 IEEE Microwave Mag. 11 58
Google Scholar
[7] Datta S 2005 Quantum Transport: Atom to Transistor (New York: Cambridge University Press
[8] Joe Y S, Satanin A M, Kim C S 2006 Phys. Scr. 74 259
Google Scholar
[9] Griffiths D J 2004 Introduction to Quantum Mechanics (2nd Ed.) (Boston: Addison-Wesley
[10] Soriano A, Navarro E A, Portì J A, Such V 2004 J. Appl. Phys 95 8011
Google Scholar
[11] Sullivan D M, Citrin D S 2005 J. Appl. Phys. 97 104305
Google Scholar
[12] Zhu M, Wang Y 2020 2020 Cross Strait Radio Science & Wireless Technology Conference (CSRSWTC), Fuzhou, China, October 11–14, 2020 p1
[13] Decleer P, Van Londersele A, Rogier H, Vande Ginste D 2021 J. Comput. Appl. Math. 381 113023
Google Scholar
[14] 沈晶, 沙威, 黄志祥, 陈明生, 吴先良 2012 61 190202
Google Scholar
Shen J, Sha Wei E I, Huang Z X, Chen M S, Wu X L 2012 Acta Phys. Sin. 61 190202
Google Scholar
[15] Taflove A, Hagness S C 2005 Computational Electrodynamics: the Finite-Difference Time-Domain Method (3rd Ed.) (Boston: Artech House
[16] Sarris C D 2011 IEEE Microwave Wireless Compon. Lett. 21 176
Google Scholar
[17] Chang C, Sarris C D 2013 IEEE Trans. Microwave Theory Tech. 61 351
Google Scholar
[18] Gao Y J, Zhang J H, Yao Z X 2019 J. Comput. Phys. 397 108853
Google Scholar
[19] Decleer P 2018 M. S. Thesis (Ghent: Ghent University
[20] Cao Q, Chen Y, Mittra R 2002 IEEE Trans. Microwave Theory Tech. 50 1578
Google Scholar
下载:
计量
- 文章访问数: 2305
- PDF下载量: 118
- 被引次数: 0
