-
高压放电充气毛细管可产生等离子体通道, 用于激光尾波加速. 为探究尾波级联加速所使用毛细管内的气体流动及分布规律, 本文建立了基于标准k-ε模型的弯曲毛细管内气体流动计算模型. 以氦气为工质, 对弯曲毛细管内可压气体流动过程进行数值模拟, 分析了不同结构、充气背压、充气口位置对毛细管内气体密度分布及速度场的影响. 结果表明: 双侧对冲弯曲毛细管在充气口之间管段具有较为稳定的气体密度分布, 充气口附近气体密度波动随充气口与毛细管两端距离的增大而减小; 在“直+弯”结构的级联加速毛细管中, 负责电子注入的直通道口径会对弯管内气体密度分布造成影响, 当电子注入通道口径小于150 μm时, 弯曲毛细管内气体流动受到直通道的影响较小, 可作为级联结构中的电子束导引通道.
Based on the standard k-ε model, a gas flow calculation model in a curved capillary is established, and the flow process of helium working medium in a curved capillary with gradually changing curvature is numerically simulated. Compared with other methods of studying micro-scale gas flow, this simulation obtains the gas density distribution in the curved capillary more conveniently, and has the same variation trend as the experimental measurement of the plasma electron density distribution, and can predict the gas flow distribution in the tube more accurately. The situation provides a theoretical basis for designing the discharge capillary experiment. Based on this model, the gas flow process in the capillary of the one-sided direct flushing, double-sided hedging and “straight + curved” cascade acceleration structures are numerically simulated. The results and conclusions are summarized as follows. 1) Comparing with the single-sided straight-bent capillary structure, the gas density fluctuation between the left gas inlet and the right gas inlet of the double-sided hedging-bend capillary is smaller, the gas flow is more stable, and a relatively stable plasma density channel can be generated. 2) In the double-sided hedged curved capillary, a relatively uniform gas density distribution is formed between the two inlets of the capillary under the same inflation back pressure; further research results show that a more uniform plasma density distribution with different lengths can be obtained by controlling the position of the gas inlet. 3) In the “traight + curved” cascaded accelerating capillary structure, the diameter of the electron injection channel will affect the gas density distribution in the bend. When the diameter of the electron injection channel is small, the absolute pressure in the capillary is low. The larger pressure difference between them will lead to a higher gas flow rate in the elbow, which will increase the fluctuation of the gas density in the elbow; the final research shows that the diameters of the electron injection channel, 100 μm and 150 μm are more suitable for the application in the “direct + bend” cascade acceleration capillary structure design. In summary, the calculation model of gas flow in the curved capillary constructed in this paper can accurately predict the gas flow distribution in the tube. The double-sided hedged curved capillary can generate a relatively stable plasma density channel, and the electron injection channel diameters, 100 μm and 150 μm, are more suitable for application in the “straight + curved” cascade accelerating capillary structure design. The research results obtained are expected to provide theoretical guidance and technical support for the laser wake cascade acceleration experiment based on the curved capillary with gradually changing curvature. -
Keywords:
- curved capillary /
- compressive flow /
- gas density /
- laser wakefield acceleration
[1] 陈民, 刘峰, 李博原, 翁苏明, 陈黎明, 盛政明, 张杰 2020 强激光与粒子束 32 7
Google Scholar
Chen M, Liu F, Li B Y, Weng S M, Chen L M, Sheng Z M, Zhang J 2020 High Power Laser Particle Beams 32 7
Google Scholar
[2] Esarey E, Schroeder C B, Leemans W P 2009 Rev. Mod. Phys. 81 1229
Google Scholar
[3] Geddes C G R, Toth C, van Tilborg J, Esarey E, Schroeder C B, Bruhwiler D, Nieter C, Cary J, Leemans W P 2004 Nature 431 538
Google Scholar
[4] Leemans W, Esarey E 2009 Phys. Today 62 44
Google Scholar
[5] Gonsalves A J, Rowlands-Rees T P, Broks B H, van der Mullen J J, Hooker S M 2007 Phys. Rev. Lett. 98 025002
Google Scholar
[6] Zigler A, Botton M, Ferber Y, Johansson G, Pollak O, Dekel E, Filippi F, Anania M P, Bisesto F, Pompili R, Ferrario M 2018 Appl. Phys. Lett. 113 183505
Google Scholar
[7] 祝昕哲, 李博原, 刘峰, 李建龙, 毕择武, 鲁林, 远晓辉, 闫文超, 陈民, 陈黎明, 盛政明, 张杰 2022 71 095202
Google Scholar
Zhu X Z, Li B Y, Liu F, Li J L, Bi Z W, Lu L, Yuan X H, Yan W C, Chen M, Chen L M, Sheng Z M, Zhang J 2022 Acta Phys. Sin. 71 095202
Google Scholar
[8] Gonsalves A J, Nakamura K, Daniels J, Benedetti C, Pieronek C, de Raadt T C H, Steinke S, Bin J H, Bulanov S S, van Tilborg J, Geddes C G R, Schroeder C B, Toth C, Esarey E, Swanson K, Fan-Chiang L, Bagdasarov G, Bobrova N, Gasilov V, Korn G, Sasorov P, Leemans W P 2019 Phys. Rev. Lett. 122 084801
Google Scholar
[9] Steinke S, van Tilborg J, Benedetti C, Geddes C G, Schroeder C B, Daniels J, Swanson K K, Gonsalves A J, Nakamura K, Matlis N H, Shaw B H, Esarey E, Leemans W P 2016 Nature 530 190
Google Scholar
[10] Luo J, Chen M, Wu W Y, Weng S M, Sheng Z M, Schroeder C B, Jaroszynski D A, Esarey E, Leemans W P, Mori W B, Zhang J 2018 Phys. Rev. Lett. 120 154801
Google Scholar
[11] Biagioni A, Anania M P, Arjmand S, Behar E, Costa G, Del Dotto A, Ferrario M, Galletti M, Lollo V, Pellegrini D, Di Pirro G, Pompili R, Raz Y, Russo G, Zigler A 2021 Plasma Phys. Control. Fusion 63 115013
Google Scholar
[12] Yang Y, Wen C 2017 Sep. Purif. Technol. 174 22
Google Scholar
[13] Peng M, Chen L, Ji W T, Tao W Q 2020 Int. J. Heat Mass Transf. 157 119982
Google Scholar
[14] Qin M, Liao K, Chen S, He G, Zhang S 2023 Chem. Eng. Res. Des. 190 605
Google Scholar
[15] 闫寒, 张文明, 胡开明, 刘岩, 孟光 2013 62 174701
Google Scholar
Yan H, Zhang W M, Hu K M, Liu Y, Meng G 2013 Acta Phys. Sin. 62 174701
Google Scholar
[16] 闫晨帅, 徐进良 2020 69 044401
Google Scholar
Yan C S, Xu J L 2020 Acta Phys. Sin. 69 044401
Google Scholar
[17] 顾娟, 黄荣宗, 刘振宇, 吴慧英 2017 66 114701
Google Scholar
Gu J, Huang R Z, Liu Z Y, Wu H Y 2017 Acta Phys. Sin. 66 114701
Google Scholar
[18] Dai W, Wu H, Liu Z Y, Zhang S 2022 Phys. Rev. E 105 025310
Google Scholar
[19] Jeong N, Lin C L, Choi D H 2006 J. Micromech. Microeng. 16 1741
Google Scholar
[20] 王佐, 刘雁, 张家忠 2016 65 014703
Google Scholar
Wang Z, Liu Y, Zhang J Z 2016 Acta Phys. Sin. 65 014703
Google Scholar
[21] Xue H, Fan Q, Shu C 2000 Probab. Eng. Eng. Mech. 15 213
Google Scholar
[22] Wang M, Li Z 2004 Int. J. Heat Fluid Flow 25 975
Google Scholar
[23] Shariati V, Ahmadian M H, Roohi E 2019 Sci. Rep. 9 17183
Google Scholar
[24] Li J L, Li B Y, Zhu X Z, Bi Z W, Wen X H, Lu L, Yuan X H, Liu F, Chen M 2023 High Power Laser Sci. Eng. 11 E58
Google Scholar
[25] Deng H, Zhang Z, Chen M, Li J, Cao Q, Hu X 2023 Materials 16 3278
Google Scholar
[26] Zhu X Z, Li B Y, Liu F, Li J L, Bi Z W, Ge X L, Deng H Y, Zhang Z Y, Cui P L, Lu L, Yan W C, Yuan X H, Chen L M, Cao Q, Liu Z Y, Sheng Z M, Chen M, Zhang J 2023 Phys. Rev. Lett. 130 215001
Google Scholar
-
图 2 弯曲毛细管结构网格划分及边界设置
Fig. 2. Mesh division and boundary setting of curved capillary structure.
图 3 实验等离子体密度与模拟气体密度对比图 (a)实验等离子体密度; (b)模拟毛细管中心轴线上气体密度
Fig. 3. Comparison of experimental plasma density and simulated gas density: (a) Experimental plasma density; (b) simulated gas density on the central axis of the capillary.
图 4 模拟计算域气体流速分布
Fig. 4. Gas flow velocity distribution in the simulated computational domain.
图 5 不同充气方式和充气压力下模拟管内气体密度 (a)单侧直冲; (b)双侧对冲
Fig. 5. Gas density in the simulated tube under different inflation methods and inflation pressures: (a) One-side inflation; (b) double-side inflation
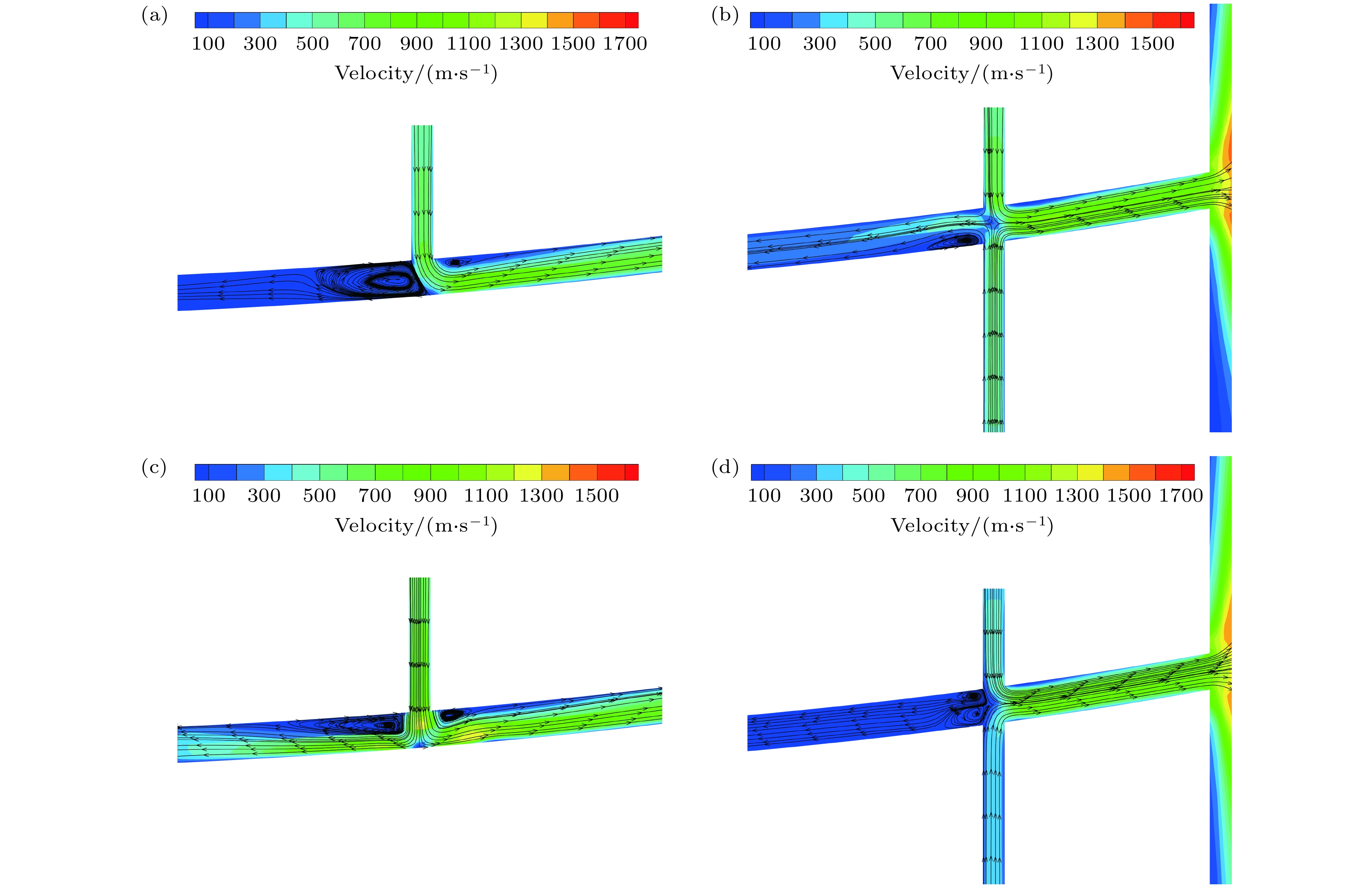
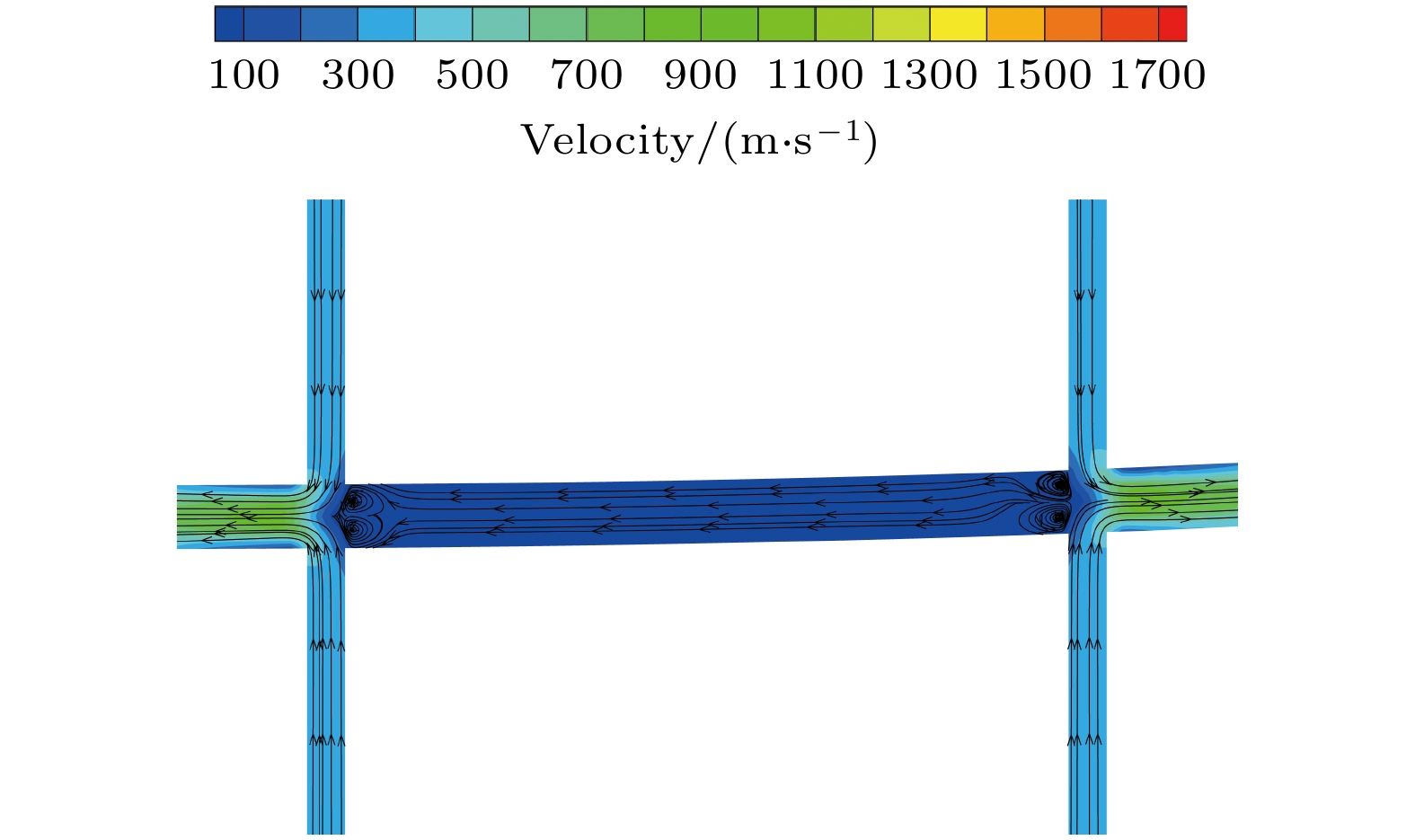
图 6 不同充气压力下, 不同充气方式管内气体流线图 (a) 68950 Pa单侧直冲; (b) 68950 Pa双侧对冲; (c) 137900 Pa单侧直冲; (d) 137900 Pa双侧对冲
Fig. 6. Gas streamlines in the simulated pipe with different inflation methods: (a) One-side inflation under 68950 Pa; (b) double-side inflation under 68950 Pa; (c) one-side inflation under 137900 Pa; (d) double-side inflation under 137900 Pa.
图 7 不同充气口位置毛细管中心轴线上气体密度
Fig. 7. Gas density on the central axis of the capillary at different gas filling positions.
图 8 充气位置距毛细管两端12 mm时, 充气口之间流线图
Fig. 8. Streamline diagram between the left and right inflation port at 12 mm from both ends of the capillary.
图 9 充气位置距毛细管两端12 mm时, 充气口之间压力云图
Fig. 9. Pressure cloud diagram between the left and right inflation port at 12 mm from both ends of the capillary.
图 10 “直+弯”放电毛细管结构示意图
Fig. 10. Schematic diagram of the “straight + curved” discharge capillary.
图 11 不同电子注入通道口径下弯曲毛细管内的气体密度分布 (a)直管径50 μm; (b)直管径100 μm; (c)直管径150 μm; (d)直管径200 μm; (e)直管径300 μm
Fig. 11. Gas density distribution in curved capillary tubes with different electron injection channel diameters: (a) 50 μm diameter; (b) 100 μm diameter; (c) 150 μm diameter; (d) 200 μm diameter; (e) 300 μm diameter.
图 12 不同电子注入通道口径下弯曲毛细管内的气体流速分布图 (a)直管径50 μm; (b)直管径100 μm; (c)直管径150 μm; (d)直管径200 μm; (e)直管径300 μm
Fig. 12. Gas velocity distribution in curved capillary tubes with different electron injection channel diameters: (a) 50 μm diameter; (b) 100 μm diameter; (c) 150 μm diameter; (d) 200 μm diameter; (e) 300 μm diameter.
表 1 网格无关性验证
Table 1. Grid independence verification.
网格数 管内气体
流速/(m·s–1)与前计算值的相对
误差绝对值/%6581 586 59.23 11524 368 29.50 26044 533 15.48 39977 452 4.63 70628 432 3.57 160003 448 — 
下载: 导出CSV
表 2 物性参数表
Table 2. Physical parameters.
比热容/
(J·kg–1)导热系数/
(W·m–1·K–1)黏度/
(Pa·s)分子质量/
(kg·kmol–1)氦气 5193 0.152 1.99 × 10–5 4.0026
下载: 导出CSV
-
[1] 陈民, 刘峰, 李博原, 翁苏明, 陈黎明, 盛政明, 张杰 2020 强激光与粒子束 32 7
Google Scholar
Chen M, Liu F, Li B Y, Weng S M, Chen L M, Sheng Z M, Zhang J 2020 High Power Laser Particle Beams 32 7
Google Scholar
[2] Esarey E, Schroeder C B, Leemans W P 2009 Rev. Mod. Phys. 81 1229
Google Scholar
[3] Geddes C G R, Toth C, van Tilborg J, Esarey E, Schroeder C B, Bruhwiler D, Nieter C, Cary J, Leemans W P 2004 Nature 431 538
Google Scholar
[4] Leemans W, Esarey E 2009 Phys. Today 62 44
Google Scholar
[5] Gonsalves A J, Rowlands-Rees T P, Broks B H, van der Mullen J J, Hooker S M 2007 Phys. Rev. Lett. 98 025002
Google Scholar
[6] Zigler A, Botton M, Ferber Y, Johansson G, Pollak O, Dekel E, Filippi F, Anania M P, Bisesto F, Pompili R, Ferrario M 2018 Appl. Phys. Lett. 113 183505
Google Scholar
[7] 祝昕哲, 李博原, 刘峰, 李建龙, 毕择武, 鲁林, 远晓辉, 闫文超, 陈民, 陈黎明, 盛政明, 张杰 2022 71 095202
Google Scholar
Zhu X Z, Li B Y, Liu F, Li J L, Bi Z W, Lu L, Yuan X H, Yan W C, Chen M, Chen L M, Sheng Z M, Zhang J 2022 Acta Phys. Sin. 71 095202
Google Scholar
[8] Gonsalves A J, Nakamura K, Daniels J, Benedetti C, Pieronek C, de Raadt T C H, Steinke S, Bin J H, Bulanov S S, van Tilborg J, Geddes C G R, Schroeder C B, Toth C, Esarey E, Swanson K, Fan-Chiang L, Bagdasarov G, Bobrova N, Gasilov V, Korn G, Sasorov P, Leemans W P 2019 Phys. Rev. Lett. 122 084801
Google Scholar
[9] Steinke S, van Tilborg J, Benedetti C, Geddes C G, Schroeder C B, Daniels J, Swanson K K, Gonsalves A J, Nakamura K, Matlis N H, Shaw B H, Esarey E, Leemans W P 2016 Nature 530 190
Google Scholar
[10] Luo J, Chen M, Wu W Y, Weng S M, Sheng Z M, Schroeder C B, Jaroszynski D A, Esarey E, Leemans W P, Mori W B, Zhang J 2018 Phys. Rev. Lett. 120 154801
Google Scholar
[11] Biagioni A, Anania M P, Arjmand S, Behar E, Costa G, Del Dotto A, Ferrario M, Galletti M, Lollo V, Pellegrini D, Di Pirro G, Pompili R, Raz Y, Russo G, Zigler A 2021 Plasma Phys. Control. Fusion 63 115013
Google Scholar
[12] Yang Y, Wen C 2017 Sep. Purif. Technol. 174 22
Google Scholar
[13] Peng M, Chen L, Ji W T, Tao W Q 2020 Int. J. Heat Mass Transf. 157 119982
Google Scholar
[14] Qin M, Liao K, Chen S, He G, Zhang S 2023 Chem. Eng. Res. Des. 190 605
Google Scholar
[15] 闫寒, 张文明, 胡开明, 刘岩, 孟光 2013 62 174701
Google Scholar
Yan H, Zhang W M, Hu K M, Liu Y, Meng G 2013 Acta Phys. Sin. 62 174701
Google Scholar
[16] 闫晨帅, 徐进良 2020 69 044401
Google Scholar
Yan C S, Xu J L 2020 Acta Phys. Sin. 69 044401
Google Scholar
[17] 顾娟, 黄荣宗, 刘振宇, 吴慧英 2017 66 114701
Google Scholar
Gu J, Huang R Z, Liu Z Y, Wu H Y 2017 Acta Phys. Sin. 66 114701
Google Scholar
[18] Dai W, Wu H, Liu Z Y, Zhang S 2022 Phys. Rev. E 105 025310
Google Scholar
[19] Jeong N, Lin C L, Choi D H 2006 J. Micromech. Microeng. 16 1741
Google Scholar
[20] 王佐, 刘雁, 张家忠 2016 65 014703
Google Scholar
Wang Z, Liu Y, Zhang J Z 2016 Acta Phys. Sin. 65 014703
Google Scholar
[21] Xue H, Fan Q, Shu C 2000 Probab. Eng. Eng. Mech. 15 213
Google Scholar
[22] Wang M, Li Z 2004 Int. J. Heat Fluid Flow 25 975
Google Scholar
[23] Shariati V, Ahmadian M H, Roohi E 2019 Sci. Rep. 9 17183
Google Scholar
[24] Li J L, Li B Y, Zhu X Z, Bi Z W, Wen X H, Lu L, Yuan X H, Liu F, Chen M 2023 High Power Laser Sci. Eng. 11 E58
Google Scholar
[25] Deng H, Zhang Z, Chen M, Li J, Cao Q, Hu X 2023 Materials 16 3278
Google Scholar
[26] Zhu X Z, Li B Y, Liu F, Li J L, Bi Z W, Ge X L, Deng H Y, Zhang Z Y, Cui P L, Lu L, Yan W C, Yuan X H, Chen L M, Cao Q, Liu Z Y, Sheng Z M, Chen M, Zhang J 2023 Phys. Rev. Lett. 130 215001
Google Scholar
下载:
计量
- 文章访问数: 3693
- PDF下载量: 138
- 被引次数: 0
