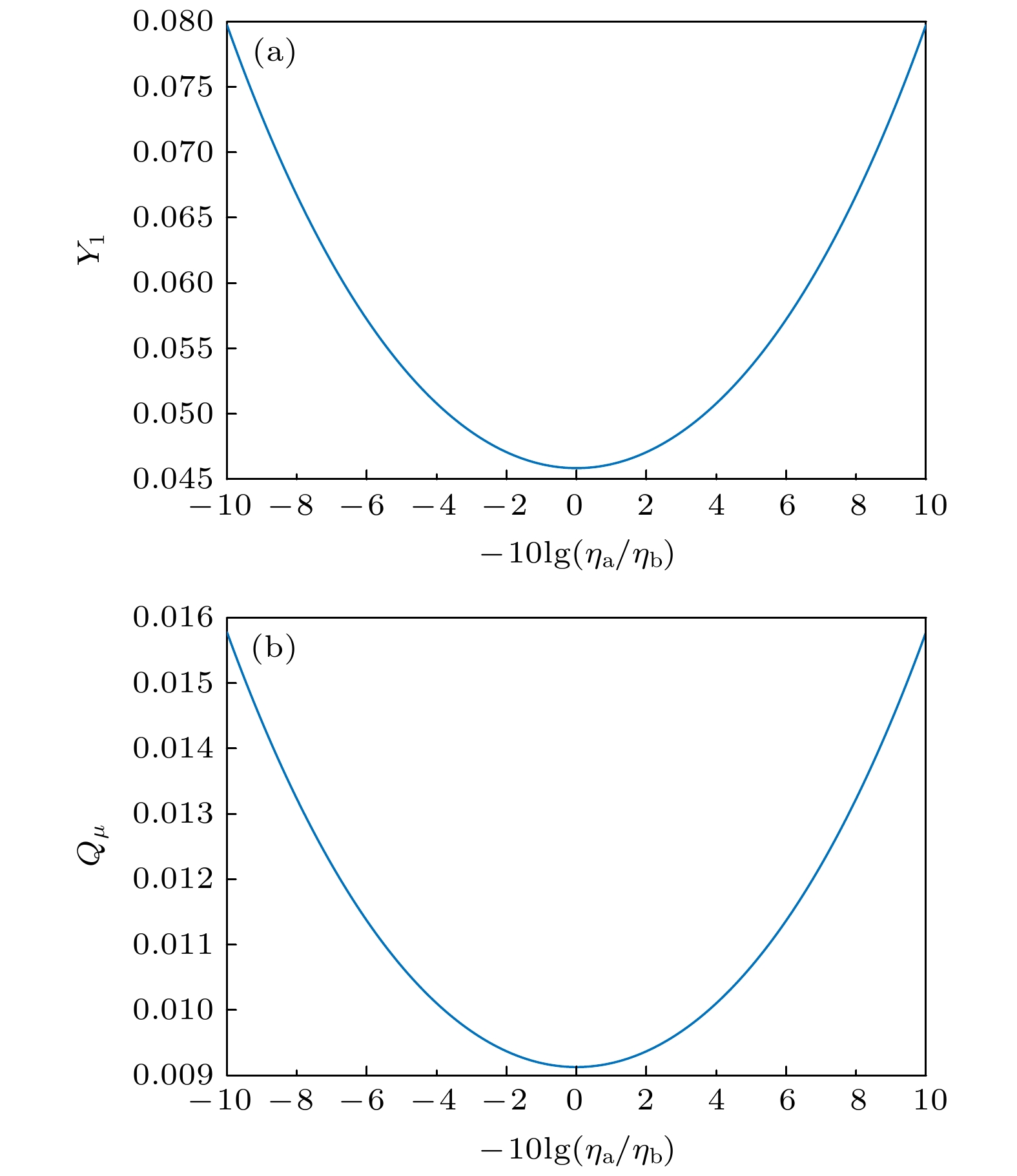
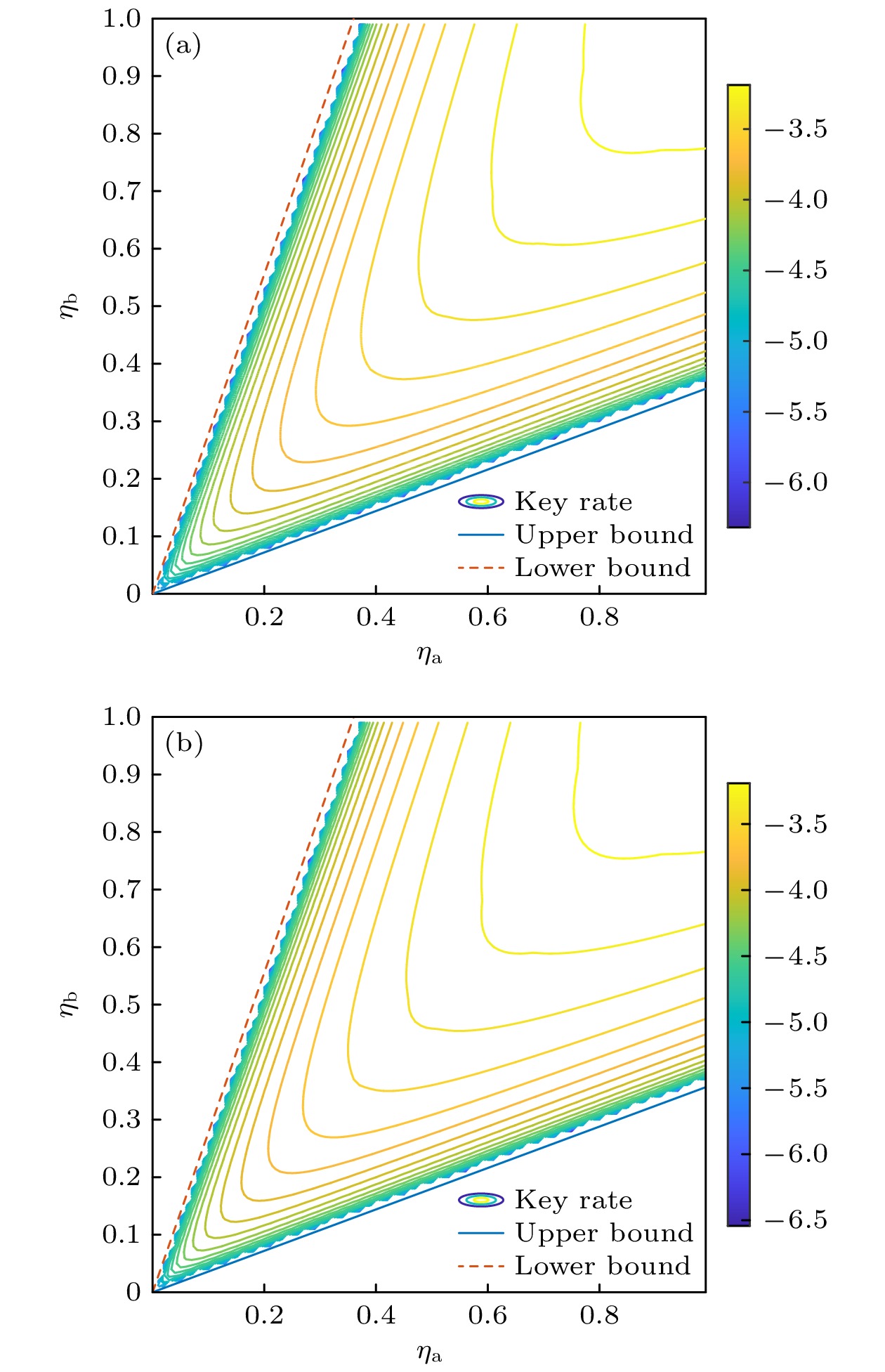
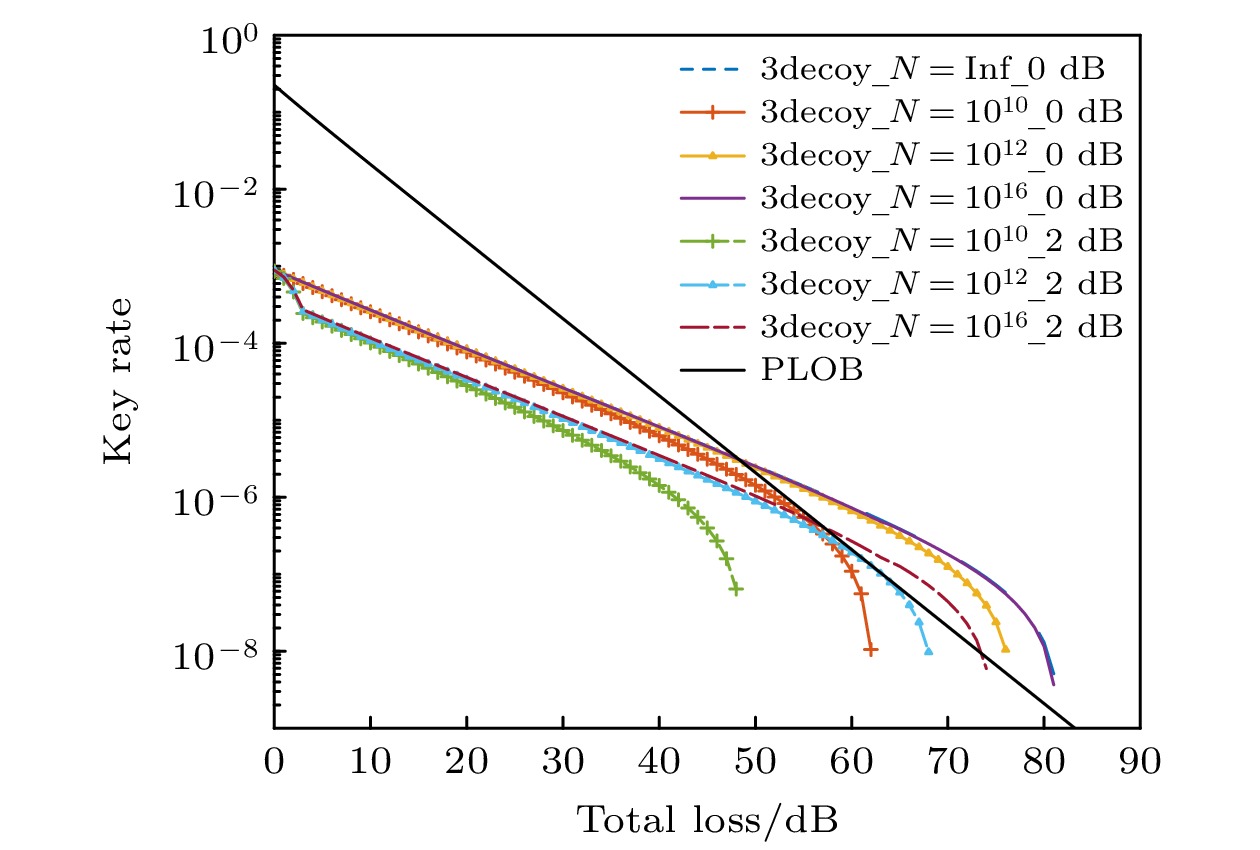
-
经典相位匹配量子密钥分发要求信道对称, 而实际应用中非对称信道应用场景更加普遍. 为研究信道非对称性对相位匹配协议性能的影响, 基于经典相位匹配协议框架提出非对称相位匹配协议, 建立相关数学仿真模型, 并对信道非对称情况下诱骗态和统计波动等对系统的影响进行仿真分析. 结果表明: 信道非对称性对系统性能影响巨大, 随着信道衰减差异的增大系统性能减小, 且减小速度逐渐加快, 超过4 dB时已无法生成密钥; 诱骗态方案不能改变系统对信道衰减差异的容忍度, 但在信道衰减差异较大时, 增加诱骗态可以显著提升系统性能; 随着数据长度的增大, 系统对信道衰减差异的容忍度逐渐提升, 当数据长度大于1012时, 这种提升不再明显, 与对称信道相比, 当信道衰减差异为2 dB时, 随着数据长度的增大, 系统性能提升更加明显.The phase-matching protocol is a practical and promising protocol that can surpass the linear key generation rate boundary. However, classical phase-matching quantum key distribution requires the channel attenuation between communicating parties to be symmetric. In practice, channels used are often asymmetric, owing to geographical reasons in a quantum key distribution network. To enhance the practicality of phase-matching, this paper proposes an asymmetric phase-matching protocol based on the classical framework and establishes a relevant mathematical simulation model to study the influence of channel asymmetry on its performance. The simulation results show that channel asymmetry significantly affects the count rate, error rate, gain, and quantum bit error rate (QBER), ultimately, system performance. As the channel attenuation difference increases, the system performance decreases and the rate of decrease accelerates. Key generation becomes impossible when the channel attenuation difference exceeds 4 dB. Although the decoy-state scheme cannot change the system's tolerance to channel attenuation difference, when the channel attenuation difference is large, the increasing of the number of decoy states significantly can improve system performance, with a three-decoy-state phase-matching protocol outperforming a two-decoy-state protocol. Considering the limited data length, the system performance is improved as the data length increases, and the tolerance to channel attenuation differences gradually increases. When the data length exceeds 1012, this improvement does not continue any more. The system cannot break through the boundary of linear key generation rate when the channel attenuation difference is 2 dB and the data length is less than 1012. Comparing with symmetric channels, the system performance improvement is very significant under asymmetric channel conditions as the data length increases.
-
Keywords:
- quantum key distribution /
- phase matching /
- asymmetric channel /
- channel attenuation difference
[1] Bennett C H, Brassard G 1984 Process IEEE International Conference Computer System Signal Processing Bangalore, India, December 9–12, 1984 pp175–179
[2] Lo H K, Ma X, Chen K 2005 Phys. Rev. Lett. 94 230504
Google Scholar
[3] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503
Google Scholar
[4] Sasaki T, Yamamoto Y, Koashi M 2014 Nature 509 475
Google Scholar
[5] Takeoka M, Guha S, Wilde M M 2014 Nat. Commun. 5 5235
Google Scholar
[6] Pirandola S, Laurenza R, Ottaviani C, Banchi L 2017 Nat. Commun. 8 15043
Google Scholar
[7] Lucamarini M, Yuan Z L, Dynes J F, Shields A J 2018 Nature 557 400
Google Scholar
[8] Ma X F, Zeng P, Zhou H Y 2018 Phys. Rev. X 8 031043
Google Scholar
[9] Xu F, Ma X, Zhang Q, Lo H K, Pan J W 2020 Rev. Mod. Phys. 92 025002
Google Scholar
[10] Lin J, Lütkenhaus N 2018 Phys. Rev. A 98 042332
Google Scholar
[11] Zeng P, Wu W, Ma X 2020 Phys. Rev. Appl. 13 064013
Google Scholar
[12] Shen Z, Chen G, Wang L, Li W, Mao Q, Zhao S 2022 Laser Phys. Lett. 19 095202
Google Scholar
[13] Yu B, Mao Q P, Zhu X M, Yu Y, Zhao S M 2021 Phys. Lett. A 418 127702
Google Scholar
[14] Yu Y, Wang L, Zhao S, Mao Q 2022 Europhys. Lett. 138 28001
Google Scholar
[15] Cui W, Song Z, Huang G, Jiao R 2022 Quantum Inf. Process. 21 313
Google Scholar
[16] Han L, Yu Y, Lu W, Xue K, Li W, Zhao S 2022 Quantum Inf. Process. 22 37
Google Scholar
[17] Li W T, Wang L, Li W, Zhao S M 2022 Chin. Phys. B 31 050310
Google Scholar
[18] Fang X T, Zeng P, Liu H, Zou M, Wu W, Tang Y L, Sheng Y J, Xiang Y, Zhang W, Li H, Wang Z, You L, Li M J, Chen H, Chen Y A, Zhang Q, Peng C Z, Ma X, Chen T Y, Pan J W 2020 Nat. Photonics 14 422
Google Scholar
[19] Ma H Q, Han Y, Dou T, Li P 2023 Chin. Phys. B 32 020304
Google Scholar
[20] Wang W, Xu F, Lo H K 2019 Phys. Rev. X 9 041012
Google Scholar
[21] Yu Y, Wang L, Zhao S, Mao Q 2021 13 th International Conference on Wireless Communications and Signal Processing Changsha, China, October 20, 2021 pp1–4
[22] Lo H K, Chau H F 1999 Science 283 2050
Google Scholar
[23] Shor P W, Preskill J 2000 Phys. Rev. Lett. 85 441
Google Scholar
[24] Wang W, Lo H K 2020 New J. Phys. 22 013020
Google Scholar
-
图 1 (a) 非对称PM协议模型; (b) 基于纠缠的PM协议模型
Fig. 1. (a) Asymmetric PM protocol model; (b) entanglement-based PM protocol model.
图 2 单光子计数率和全局增益随信道衰减差变化情况 (a)单光子计数率Y1; (b)全局增益Qμ
Fig. 2. Variation of the single-photon yield and total gain with channel attenuation difference: (a) Single photon counting rate Y1; (b) global gain Qμ.
图 3 量子比特误码率和相位错误率随信道衰减差的变化
Fig. 3. Variation of QBER and phase error rate with channel attenuation difference.
图 4 PM协议密钥生成率随信道衰减差的变化
Fig. 4. Variation of PM protocol key generation rate with channel attenuation difference.
图 5 不同信道差异时密钥生成率随信道总衰减的变化
Fig. 5. Variation of key generation rate with total channel attenuation for different channel differences.
图 6 不同诱骗态数量时密钥生成率随信道传输效率变化等高线图 (a) 二诱骗态; (b)三诱骗态
Fig. 6. The contour plot of key generation rate as a function of channel transmission efficiency for different numbers of decoy states: (a) Two-decoy-state; (b) three-decoy-state.
图 7 不同诱骗态数量时密钥生成率随信道总衰减变化情况
Fig. 7. Variation of key generation rate with total channel attenuation for different decoy states.
图 8 不同数据长度情况下密钥生成率随信道传输率变化图像 (a) N = 108; (b) N = 1010; (c) N = 1012; (d) N = 1016
Fig. 8. Image of key generation rate changing with channel transmission rate under different data lengths: (a) N = 108; (b) N = 1010; (c) N = 1012; (d) N = 1016.
图 9 不同信道衰减差情况下数据长度对密钥生成率的影响
Fig. 9. Effect of data length on key rate under different channel attenuation differences.
表 1 主要仿真参数
Table 1. The Main parameters in numerical simulations.
参数 暗记数
pd纠错
效率$ f $相位分
片数$ M $置信度
1 – θ取值 $ 8 \times {10^{ - 8}} $ 1.15 16 $1-5.73 \times {10^{ - 7} }$ 
下载: 导出CSV
-
[1] Bennett C H, Brassard G 1984 Process IEEE International Conference Computer System Signal Processing Bangalore, India, December 9–12, 1984 pp175–179
[2] Lo H K, Ma X, Chen K 2005 Phys. Rev. Lett. 94 230504
Google Scholar
[3] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503
Google Scholar
[4] Sasaki T, Yamamoto Y, Koashi M 2014 Nature 509 475
Google Scholar
[5] Takeoka M, Guha S, Wilde M M 2014 Nat. Commun. 5 5235
Google Scholar
[6] Pirandola S, Laurenza R, Ottaviani C, Banchi L 2017 Nat. Commun. 8 15043
Google Scholar
[7] Lucamarini M, Yuan Z L, Dynes J F, Shields A J 2018 Nature 557 400
Google Scholar
[8] Ma X F, Zeng P, Zhou H Y 2018 Phys. Rev. X 8 031043
Google Scholar
[9] Xu F, Ma X, Zhang Q, Lo H K, Pan J W 2020 Rev. Mod. Phys. 92 025002
Google Scholar
[10] Lin J, Lütkenhaus N 2018 Phys. Rev. A 98 042332
Google Scholar
[11] Zeng P, Wu W, Ma X 2020 Phys. Rev. Appl. 13 064013
Google Scholar
[12] Shen Z, Chen G, Wang L, Li W, Mao Q, Zhao S 2022 Laser Phys. Lett. 19 095202
Google Scholar
[13] Yu B, Mao Q P, Zhu X M, Yu Y, Zhao S M 2021 Phys. Lett. A 418 127702
Google Scholar
[14] Yu Y, Wang L, Zhao S, Mao Q 2022 Europhys. Lett. 138 28001
Google Scholar
[15] Cui W, Song Z, Huang G, Jiao R 2022 Quantum Inf. Process. 21 313
Google Scholar
[16] Han L, Yu Y, Lu W, Xue K, Li W, Zhao S 2022 Quantum Inf. Process. 22 37
Google Scholar
[17] Li W T, Wang L, Li W, Zhao S M 2022 Chin. Phys. B 31 050310
Google Scholar
[18] Fang X T, Zeng P, Liu H, Zou M, Wu W, Tang Y L, Sheng Y J, Xiang Y, Zhang W, Li H, Wang Z, You L, Li M J, Chen H, Chen Y A, Zhang Q, Peng C Z, Ma X, Chen T Y, Pan J W 2020 Nat. Photonics 14 422
Google Scholar
[19] Ma H Q, Han Y, Dou T, Li P 2023 Chin. Phys. B 32 020304
Google Scholar
[20] Wang W, Xu F, Lo H K 2019 Phys. Rev. X 9 041012
Google Scholar
[21] Yu Y, Wang L, Zhao S, Mao Q 2021 13 th International Conference on Wireless Communications and Signal Processing Changsha, China, October 20, 2021 pp1–4
[22] Lo H K, Chau H F 1999 Science 283 2050
Google Scholar
[23] Shor P W, Preskill J 2000 Phys. Rev. Lett. 85 441
Google Scholar
[24] Wang W, Lo H K 2020 New J. Phys. 22 013020
Google Scholar
下载:
计量
- 文章访问数: 2527
- PDF下载量: 66
- 被引次数: 0
