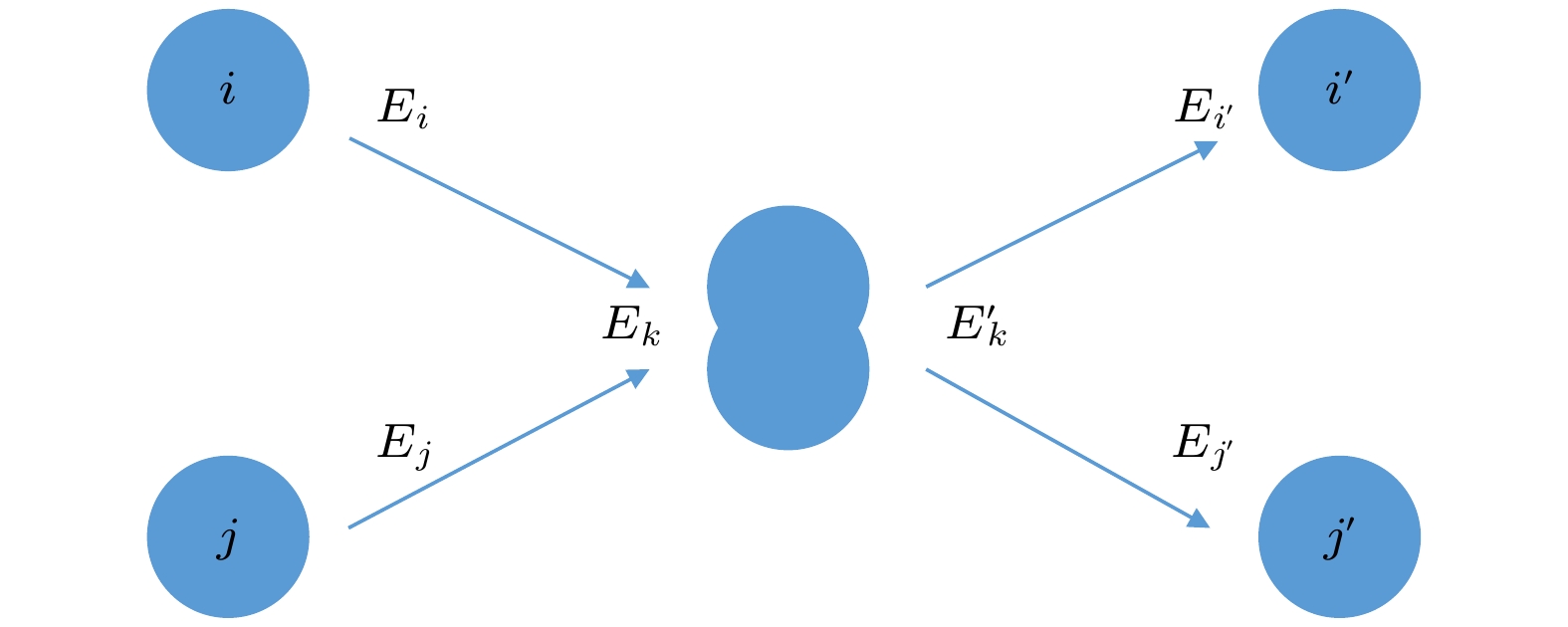
-
镥-177是目前全球医用同位素的研究热点之一, 可使用通过电子束物理气相沉积技术(EB-PVD)辅助生产和加工的镥-176经由反应堆辐照制得. 金属蒸发过程是EB-PVD的重要一环, 金属原子蒸气的各宏观特征量分布将直接影响后续的沉积镀膜过程. 本文基于直接模拟蒙特卡罗方法, 将原子亚稳态引入碰撞假设, 建立了金属蒸发过程的二维和三维模型, 对是否考虑镥原子亚稳态的金属蒸发过程中各宏观特征量进行分析比较, 并对中心处宏观特征量随狭缝开口大小和蒸发源表面温度的变化特点进行讨论. 研究结果表明, 原子亚稳态会导致经过束流装置的金属原子蒸气数密度降低、运动速度和速度的离散程度上升, 同时狭缝开口大小和蒸发源表面温度均会引发金属原子蒸气宏观特征量分布的变化. 在二维模型基础上进行的三维模拟结果与其变化一致, 本工作可为电子束金属蒸发过程的实验研究提供参考和指导.
-
关键词:
- 直接模拟蒙特卡罗方法 /
- 镥 /
- 原子亚稳态 /
- 金属蒸发
Lutetium-177, one of the current global research hotspots for medical isotopes, can be produced by reactor irradiation of lutetium-176, which can be produced and processed with the assistance of the electron beam physical vapor deposition (EB-PVD). The metal evaporation process is an important part of EB-PVD, which aims to convert solid metal into metal atomic vapor. The distribution of each macroscopic characteristic quantity, such as thermal population distribution, density distribution, velocity distribution, and temperature distribution of metal atomic vapor, will directly affect the utilization of metal vapor atoms, the subsequent deposition process, and coating process. In this paper, two-dimensional model and three-dimensional model of the metal evaporation process are established based on the direct simulation Monte Carlo method, and atomic metastable state is introduced into the collision assumption. The macroscopic characteristic quantities, such as the number density of metal atomic vapor, the motion velocity and the discrete degree of the total motion velocity in the evaporation process with or without considering the lutetium atomic metastable state, are analyzed and compared. The spatial distribution characteristics of each energy level of metal atomic vapor are observed, and the variation characteristics of the macroscopic characteristic quantities in the center with the slit opening size and the evaporation source surface temperature are discussed. The study results show that the number density of metal vapor passing through the beam flow device decreases, the average velocity in the x-direction and z-direction and the discrete degree of the total motion velocity increase, with the atomic metastable state taken into consideration. The beam flow device intensifies the transformation of the atomic energy level of the metal vapor and changes the physical parameters of the metal atomic vapor. At the same time, the slit opening size and the evaporation source surface temperature trigger off the change of the macroscopic characteristic quantity distribution of the metal vapor, including the degree of anomalous protrusion of each macroscopic characteristic quantity above the slit. The results of the three-dimensional simulation based on the two-dimensional model are consistent with the changes in the order of magnitude of data distribution and spatial distribution pattern, which can serve as a reference and guidance for the experimental study of the electron beam metal evaporation process.-
Keywords:
- direct simulation Monte Carlo method /
- lutetium /
- atomic metastable state /
- metal evaporation
[1] 卓连刚, 杨宇川, 岳海东, 熊晓玲, 王关全, 王海麟, 杨林, 林青川, 陈琪萍, 涂俊, 魏洪源 2022 同位素 35 217
Google Scholar
Zhuo L G, Yang Y C, Yue H D, Xiong X L, Wang G Q, Wang H L, Yang L, Lin Q C, Chen Q P, Tu J, Wei H Y 2022 J. Isot. 35 217
Google Scholar
[2] Bournaud C, Kelly A, Hindié E, Tenenbaum F, Faivre-Chauvet A, Courbon F, Taïeb D, Dierickx L O, Coriat R, Ansquer C 2017 Med. Nucl. 41 42
Google Scholar
[3] Strosberg J, El-Haddad G, Wolin E, Hendifar A, Yao J, Chasen B, Mittra E, Kunz P L, Kulke M H, Jacene H, Bushnell D, O’Dorisio T M, Baum R P, Kulkarni H R, Caplin M, Lebtahi R, Hobday T, Delpassand E, Van Cutsem E, Benson A, Srirajaskanthan R, Pavel M, Mora J, Berlin J, Grande E, Reed N, Seregni E, Öberg K, Lopera Sierra M, Santoro P, Thevenet T, Erion J L, Ruszniewski P, Kwekkeboom D, Krenning E, NETTER-1 Trial Investigators 2017 N. Engl. J. Med. 376 125
Google Scholar
[4] 彭述明, 杨宇川, 谢翔, 钱达志 2020 科学通报 65 3526
Google Scholar
Peng S M, Yang Y C, Xie X, Qian D Z 2020 Chin Sci Bull 65 3526
Google Scholar
[5] 胡映江, 王磊, 吴建荣, 李波, 罗宁, 陈云明, 曾俊杰, 孙志中, 贾致军, 张劲松 2023 同位素 36 83
Google Scholar
Hu Y J, Wang L, Wu J R, Li B, Luo N, Chen Y M, Zeng J J, Sun Z Z, Jia Z J, Zhang J S 2023 J. Isot. 36 83
Google Scholar
[6] 张世宏, 王启民, 郑军 2020 气相沉积技术原理及应用 (北京: 冶金工业出版社) 第36, 37页
Zhang S H, Wang Q M, Zheng J 2020 Principle and Application of Vapor Deposition Technology (Beijing: Metallurgical Industry Press) pp36, 37
[7] 赖奇, 李俊翰, 吴恩辉, 崔晏, 李亮, 廖先杰 2020 钢铁钒钛 41 76
Google Scholar
Lai Q, Li J H, Wu E H, Cui Y, Li L, Liao X J 2020 Iron, Steel, Vanadium, Titanium 41 76
Google Scholar
[8] 杨光, 刘欢, 王丁丁, 罗立平, 吕绪明, 祁阳 2021 真空 58 81
Google Scholar
Yang G, Liu H, Wang D D, Luo L P, Lv X M, Qi Y 2021 Vacuum (Shenyang, China) 58 81
Google Scholar
[9] 滕晓丹, 彭徽, 李刘合, 郭洪波, 宫声凯 2023 航空制造技术 66 40
Google Scholar
Teng X D, Peng H, Li L H, Guo H B, Gong S K 2023 Aeronautical Manufacturing Technology 66 40
Google Scholar
[10] 王德武 1999 激光分离同位素理论及其应用 (北京: 原子能出版社) 第338—340页
Wang D W 1999 Theory and Application of Laser Isotope Separation (Beijing: Atomic Energy Press) pp338–340
[11] 谢国锋, 王德武, 应纯同 2002 51 584
Google Scholar
Xie G F, Wang D W, Ying C T 2002 Acta Phys. Sin. 51 584
Google Scholar
[12] 谢国锋, 王德武, 应纯同 2002 51 2286
Google Scholar
Xie G F, Wang D W, Ying C T 2002 Acta Phys. Sin. 51 2286
Google Scholar
[13] 翟蕊 2019 硕士学位论文 (北京: 清华大学)
Zhai R 2019 M. S. Dissertation (Beijing: Tsinghua University
[14] 卢肖勇, 张小章 2018 67 154701
Google Scholar
Lu X Y, Zhang X Z 2018 Acta Phys. Sin. 67 154701
Google Scholar
[15] Lu X Y, Zhang X Z, Zhang Z Z 2018 Chin. Phys. B 27 124702
Google Scholar
[16] Lu X Y, Chai J J 2019 Chin. Phys. B 28 074702
Google Scholar
[17] 卢肖勇 2020 博士学位论文 (北京: 清华大学)
Lu X Y 2020 Ph. D. Dissertation (Beijing: Tsinghua University
[18] Fan J, Boyd I D, Shelton C 2000 J. Vac. Sci. Technol. A 18 2937
Google Scholar
[19] Balakrishnan J, Boyd I D, Braun D G 2000 J. Vac. Sci. Technol. A 18 907
Google Scholar
[20] 谢国锋, 王德武, 应纯同 2002 原子能科学技术 36 147
Google Scholar
Xie G F, Wang D W, Ying C T 2002 Atom. Energ. Sci. Tech. 36 147
Google Scholar
[21] Bird G A 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows (New York: Oxford University Press) pp218–220
[22] 沃尔夫冈·戴姆特瑞德 著 (姬扬 译) 2012 激光光谱学 (第1卷: 基础理论) (北京: 科学出版社) 第10—13页
Demtröder W (translated by Ji Y) 2012 Laser Spectroscopy (Vol. 1: Basic Principles) (Beijing: Science Press) pp10–13
[23] 李阳 2015 硕士学位论文 (天津: 天津大学)
Li Y 2015 M. S. Dissertation (Tianjin: Tianjin University
[24] 沈青 2003 稀薄气体动力学 (北京: 国防工业出版社) 第122—127页
Shen Q 2003 Rarefied Gas Dynamics (Beijing: National Defense Industry Press) pp122–127
[25] 王权, 李小江, 陈勇, 陈英 2019 化学反应工程与工艺 35 129
Google Scholar
Wang Q, Li X J, Chen Y, Chen Y 2019 Chem. React. Eng. Technol. 35 129
Google Scholar
-
图 1 镥前5个能级的热布居分布比例
Fig. 1. Thermal population distribution proportion of lutetium’s first five energy levels.
图 2 二维非弹性碰撞的能量变化示意图
Fig. 2. Schematic diagram of the energy change in a two-dimensional inelastic collision.
图 3 二维和三维模型示意图 (a) 二维模型; (b) 三维模型
Fig. 3. Schematic diagram of two-dimensional and three-dimensional models: (a) Two-dimensional model; (b) three-dimensional model.
图 4 金属原子蒸气各宏观特征量的二维空间分布(左为不考虑原子亚稳态, 右为考虑原子亚稳态) (a) 数密度
$n$ ; (b) 总运动速度的离散程度$T$ ; (c)$x$ 方向平均速度${u_x}$ ; (d)$z$ 方向平均速度${u_z}$ Fig. 4. Two-dimensional spatial distribution of macroscopic characteristic quantities of metal atomic vapor (left is not considering atomic metastable states, right is considering atomic metastable states): (a) Number density
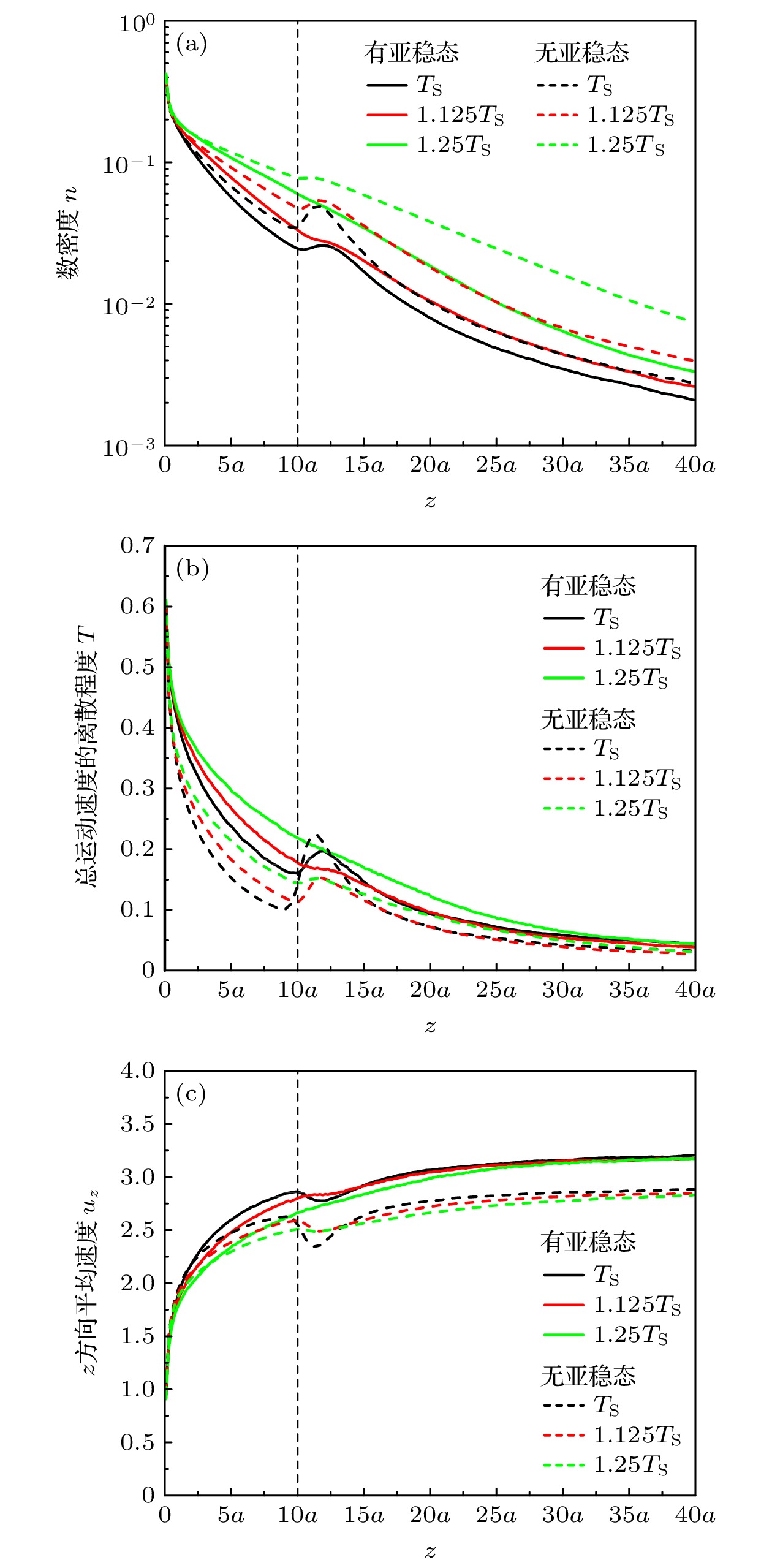
$n$ ; (b) the discrete degree of total motion velocity$T$ ; (c) average velocity${u_x}$ in the$x$ -direction; (d) average velocity${u_z}$ in the$z$ -direction.
图 5 各能级占比分布图 (a) 能级1; (b) 能级2; (c) 能级3; (d) 能级4
Fig. 5. Layout of the proportion of each energy level: (a) Energy level 1; (b) energy level 2; (c) energy level 3; (d) energy level 4.
图 6 金属原子蒸气在蒸发源中心位置处的宏观特征量变化曲线(不同狭缝开口大小) (a) 数密度
$n$ ; (b) 总运动速度的离散程度$T$ ; (c)$z$ 方向平均速度${u_z}$ Fig. 6. Variation curves of macroscopic characteristic quantities of metal atomic vapor at the center of the evaporation source (different slit opening sizes): (a) Number density
$n$ ; (b) the discrete degree of total motion velocity$T$ ; (c) average velocity${u_z}$ in the$z$ -direction.
图 7 金属原子蒸气在蒸发源中心位置处的宏观特征量变化曲线(不同蒸发源表面温度) (a) 数密度
$n$ ; (b) 总运动速度的离散程度$T$ ; (c)$z$ 方向平均速度${u_z}$ Fig. 7. Variation curves of macroscopic characteristic quantities of metal atomic vapor at the center of the evaporation source (different surface temperatures of evaporation source): (a) Number density
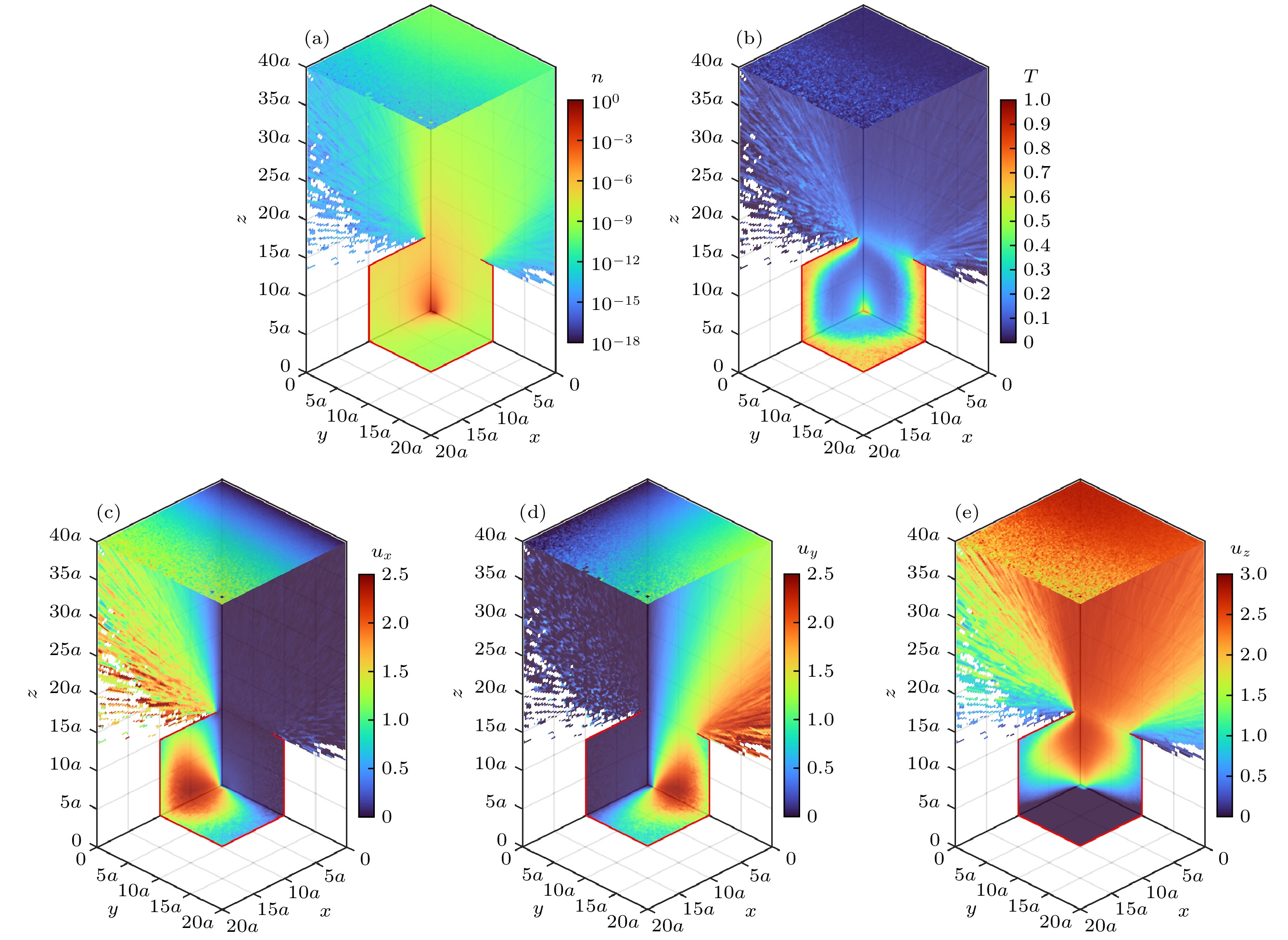
$n$ ; (b) the discrete degree of total motion velocity$T$ ; (c) average velocity${u_z}$ in the$z$ -direction.
图 8 金属原子蒸气各宏观特征量的三维空间分布 (a) 数密度
$n$ ; (b) 总运动速度的离散程度$T$ ; (c)$x$ 方向平均速度${u_x}$ ; (d)$y$ 方向平均速度${u_y}$ ; (e)$z$ 方向平均速度${u_z}$ Fig. 8. Three-dimensional spatial distribution of macroscopic characteristic quantities of metal atomic vapor: (a) Number density
$n$ ; (b) the discrete degree of total motion velocity$T$ ; (c) average velocity${u_x}$ in the$x$ -direction; (d) average velocity${u_y}$ in the$y$ -direction; (e) average velocity${u_z}$ in the$z$ -direction. -
[1] 卓连刚, 杨宇川, 岳海东, 熊晓玲, 王关全, 王海麟, 杨林, 林青川, 陈琪萍, 涂俊, 魏洪源 2022 同位素 35 217
Google Scholar
Zhuo L G, Yang Y C, Yue H D, Xiong X L, Wang G Q, Wang H L, Yang L, Lin Q C, Chen Q P, Tu J, Wei H Y 2022 J. Isot. 35 217
Google Scholar
[2] Bournaud C, Kelly A, Hindié E, Tenenbaum F, Faivre-Chauvet A, Courbon F, Taïeb D, Dierickx L O, Coriat R, Ansquer C 2017 Med. Nucl. 41 42
Google Scholar
[3] Strosberg J, El-Haddad G, Wolin E, Hendifar A, Yao J, Chasen B, Mittra E, Kunz P L, Kulke M H, Jacene H, Bushnell D, O’Dorisio T M, Baum R P, Kulkarni H R, Caplin M, Lebtahi R, Hobday T, Delpassand E, Van Cutsem E, Benson A, Srirajaskanthan R, Pavel M, Mora J, Berlin J, Grande E, Reed N, Seregni E, Öberg K, Lopera Sierra M, Santoro P, Thevenet T, Erion J L, Ruszniewski P, Kwekkeboom D, Krenning E, NETTER-1 Trial Investigators 2017 N. Engl. J. Med. 376 125
Google Scholar
[4] 彭述明, 杨宇川, 谢翔, 钱达志 2020 科学通报 65 3526
Google Scholar
Peng S M, Yang Y C, Xie X, Qian D Z 2020 Chin Sci Bull 65 3526
Google Scholar
[5] 胡映江, 王磊, 吴建荣, 李波, 罗宁, 陈云明, 曾俊杰, 孙志中, 贾致军, 张劲松 2023 同位素 36 83
Google Scholar
Hu Y J, Wang L, Wu J R, Li B, Luo N, Chen Y M, Zeng J J, Sun Z Z, Jia Z J, Zhang J S 2023 J. Isot. 36 83
Google Scholar
[6] 张世宏, 王启民, 郑军 2020 气相沉积技术原理及应用 (北京: 冶金工业出版社) 第36, 37页
Zhang S H, Wang Q M, Zheng J 2020 Principle and Application of Vapor Deposition Technology (Beijing: Metallurgical Industry Press) pp36, 37
[7] 赖奇, 李俊翰, 吴恩辉, 崔晏, 李亮, 廖先杰 2020 钢铁钒钛 41 76
Google Scholar
Lai Q, Li J H, Wu E H, Cui Y, Li L, Liao X J 2020 Iron, Steel, Vanadium, Titanium 41 76
Google Scholar
[8] 杨光, 刘欢, 王丁丁, 罗立平, 吕绪明, 祁阳 2021 真空 58 81
Google Scholar
Yang G, Liu H, Wang D D, Luo L P, Lv X M, Qi Y 2021 Vacuum (Shenyang, China) 58 81
Google Scholar
[9] 滕晓丹, 彭徽, 李刘合, 郭洪波, 宫声凯 2023 航空制造技术 66 40
Google Scholar
Teng X D, Peng H, Li L H, Guo H B, Gong S K 2023 Aeronautical Manufacturing Technology 66 40
Google Scholar
[10] 王德武 1999 激光分离同位素理论及其应用 (北京: 原子能出版社) 第338—340页
Wang D W 1999 Theory and Application of Laser Isotope Separation (Beijing: Atomic Energy Press) pp338–340
[11] 谢国锋, 王德武, 应纯同 2002 51 584
Google Scholar
Xie G F, Wang D W, Ying C T 2002 Acta Phys. Sin. 51 584
Google Scholar
[12] 谢国锋, 王德武, 应纯同 2002 51 2286
Google Scholar
Xie G F, Wang D W, Ying C T 2002 Acta Phys. Sin. 51 2286
Google Scholar
[13] 翟蕊 2019 硕士学位论文 (北京: 清华大学)
Zhai R 2019 M. S. Dissertation (Beijing: Tsinghua University
[14] 卢肖勇, 张小章 2018 67 154701
Google Scholar
Lu X Y, Zhang X Z 2018 Acta Phys. Sin. 67 154701
Google Scholar
[15] Lu X Y, Zhang X Z, Zhang Z Z 2018 Chin. Phys. B 27 124702
Google Scholar
[16] Lu X Y, Chai J J 2019 Chin. Phys. B 28 074702
Google Scholar
[17] 卢肖勇 2020 博士学位论文 (北京: 清华大学)
Lu X Y 2020 Ph. D. Dissertation (Beijing: Tsinghua University
[18] Fan J, Boyd I D, Shelton C 2000 J. Vac. Sci. Technol. A 18 2937
Google Scholar
[19] Balakrishnan J, Boyd I D, Braun D G 2000 J. Vac. Sci. Technol. A 18 907
Google Scholar
[20] 谢国锋, 王德武, 应纯同 2002 原子能科学技术 36 147
Google Scholar
Xie G F, Wang D W, Ying C T 2002 Atom. Energ. Sci. Tech. 36 147
Google Scholar
[21] Bird G A 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows (New York: Oxford University Press) pp218–220
[22] 沃尔夫冈·戴姆特瑞德 著 (姬扬 译) 2012 激光光谱学 (第1卷: 基础理论) (北京: 科学出版社) 第10—13页
Demtröder W (translated by Ji Y) 2012 Laser Spectroscopy (Vol. 1: Basic Principles) (Beijing: Science Press) pp10–13
[23] 李阳 2015 硕士学位论文 (天津: 天津大学)
Li Y 2015 M. S. Dissertation (Tianjin: Tianjin University
[24] 沈青 2003 稀薄气体动力学 (北京: 国防工业出版社) 第122—127页
Shen Q 2003 Rarefied Gas Dynamics (Beijing: National Defense Industry Press) pp122–127
[25] 王权, 李小江, 陈勇, 陈英 2019 化学反应工程与工艺 35 129
Google Scholar
Wang Q, Li X J, Chen Y, Chen Y 2019 Chem. React. Eng. Technol. 35 129
Google Scholar
下载:
计量
- 文章访问数: 2852
- PDF下载量: 71
- 被引次数: 0
