-
皮质骨是一种高衰减、各向异性、高声阻抗的多层生物组织. 其结构和材料特性导致高频超声难以穿透其多层结构, 从而获取高质量图像. 传统超声动态聚焦成像以均匀声速假设为前提, 且受制于发射能量和帧率, 难以实现多层结构的准确、快速重建, 限制其临床应用的推广. 针对以上问题, 本文提出一种基于相位迁移的平面波骨成像方法(PSM-PW-VI), 实现了皮质骨多层结构的精确和快速重建. 首先利用超声走时反演估计成像区域的声速分布; 然后应用频域相位迁移平面波相干复合方法并行重建上下两个相控阵探头对应的超声图像; 最后将两幅图像融合得到完整的皮质骨超声图像. 仿真、仿体、离体实验共同验证了该方法的有效性. 无论是三层还是五层模型的皮质骨, 其厚度的平均误差均小于0.2 mm, 相对误差小于7%. 此外, 与基于相位迁移合成孔径(PSM-SA)方法相比, 在相同的工作频率下, 该方法具有更深的成像深度和更快的成像速度. 实验结果表明, 该方法是一种准确高效的皮质骨超声成像方法, 对超声骨成像技术的发展和临床研究具有一定的借鉴意义.Cortical bone, a highly attenuated, anisotropic, and multilayered biological medium with high acoustic impedance, presents significant challenges for high-frequency ultrasound to penetrate its complex structure and acquire high-quality images. The traditional method of using uniform sound velocity in ultrasonic dynamic focusing imaging is limited by emission energy and frame rate, which hinders the accurate and rapid reconstruction of multi-layer structures and clinical applications. In order to meet these challenges, this study proposes a novel method, called the phase shift migration-based plane-wave bone imaging via velocity inversion (PSM-PW-VI), that can accurately and quickly image the multi-layer structure of cortical bone. In the PSM-PW-VI method, two identical linear array probes are arranged in parallel on both sides of the cortical bone for data acquisition. First, the ultrasound velocity distribution in the imaging region is obtained by using ultrasound travel time inversion. Next, two images corresponding to the upper probe and lower probe are acquired in parallel in the frequency domain by employing a phase shift migration-based coherent plane-wave compounding method. Finally, the two images are merged to generate a complete ultrasound image of the cortical bone. Wave propagation in cortical bone is simulated by using the open source toolbox k-wave in MATLAB. Ex-vivo experiments are conducted on 2.5-mm-thick sawbones phantom and 2.45-mm-thick bovine bone plates to evaluate the feasibility of the proposed method, by using the Verasonics platform. Simulation, phantom (Sawbones), and ex-vivo experiments validate the effectiveness of the method. Notably, the average error of the thickness is less than 0.2 mm, and the relative error is less than 7% for both three-layer and five-layer cortical bone. The influence of the number of plane wave compounding angles on imaging quality is investigated, revealing that only 15 angles are sufficient to produce high-quality images. The influence of the velocity model on imaging accuracy is also examined since accurate sound velocity estimation is crucial for obtaining high-quality images of cortical bone. Finally, the performances of PSM-PW-VI and PSM-SA in imaging depth and efficiency are compared. The results demonstrate that the proposed PSM-PW-VI method offers significant improvements in temporal resolution, data storage and processing quantity, emission energy, and imaging depth. The experimental findings validate the effectiveness of the proposed method as an accurate and efficient ultrasound imaging tool for cortical bone, and its substantial role in promoting ultrasound bone imaging technology and clinical applications.
-
Keywords:
- plane wave imaging /
- cortical bone /
- multilayered medium /
- frequency domain
[1] Compston J E, McClung M R, Leslie W D 2019 Lancet 393 364
 Google Scholar
Google Scholar
[2] 杨慧林 2022 中华骨与关节外科杂志 15 652
 Google Scholar
Google Scholar
Yang H L 2022 Chin. J. Bone Joint Surg. 15 652
 Google Scholar
Google Scholar
[3] Langton C M, Njeh C F 2008 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 55 1546
 Google Scholar
Google Scholar
[4] 东蕊, 刘成成, 蔡勋兵, 邵留磊, 李博艺, 他得安 2019 68 150
 Google Scholar
Google Scholar
Dong R, Liu C C, Cai X B, Shao L L, Li B Y, Ta D A 2019 Acta Phys. Sin. 68 150
 Google Scholar
Google Scholar
[5] Moilanen P, Nicholson Patrick H F, Kilappa V, Cheng, Timonen 2007 Ultrasound Med. Biol. 33 254
 Google Scholar
Google Scholar
[6] Minonzio J G, Talmant M, Laugier P 2010 J. Acoust. Soc. Am. 127 2913
 Google Scholar
Google Scholar
[7] Manes G, Tortoli P, Andreuccetti F, Avitabile G, Atzeni C 1988 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 35 14
 Google Scholar
Google Scholar
[8] Adams R B 2022 Surg. Open Sci. 10 182
 Google Scholar
Google Scholar
[9] Weismann C, Mayr C, Egger H, Auer A 2011 Breast Care 6 98
 Google Scholar
Google Scholar
[10] Zu Siederdissen C H, Potthoff A 2020 Internist 61 115
 Google Scholar
Google Scholar
[11] Nguyen Minh H, Du J, Raum K 2020 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 67 568
 Google Scholar
Google Scholar
[12] Nowicki A, Gambin B 2014 Arch. Acoust. 39 427
 Google Scholar
Google Scholar
[13] 孙宝申, 沈建中 1993 应用声学 3 43
 Google Scholar
Google Scholar
Sun B S, Shen J Z 1993 Appl. Acoust. 3 43
 Google Scholar
Google Scholar
[14] Renaud G, Kruizinga P, Cassereau D, Laugier P 2018 Phys. Med. Biol. 63 125010
 Google Scholar
Google Scholar
[15] 李云清, 江晨, 李颖, 徐峰, 许凯亮, 他得安, 黎仲勋 2019 68 184302
 Google Scholar
Google Scholar
Li Y Q, Jiang C, Li Y, Xu F, Xu K L, Ta D A, Li Z X 2019 Acta Phys. Sin. 68 184302
 Google Scholar
Google Scholar
[16] Jiang C, Li Y, Li B, Liu C, Xu F, Xu K, Ta D 2019 IEEE Access 7 163013
 Google Scholar
Google Scholar
[17] Jiang C, Li Y, Xu K L, Ta D A 2021 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 68 72
 Google Scholar
Google Scholar
[18] Li Y F, Shi Q Z, Liu Y, Gu M L, Liu C C, Song X J, Ta D A, Wang W Q 2021 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 68 2619
 Google Scholar
Google Scholar
[19] Montaldo G, Tanter M, Bercoff J, Benech N, Fink M 2009 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56 489
 Google Scholar
Google Scholar
[20] Bercoff J, Montaldo G, Loupas T, Savery D, Meziere F, Fink M, Tanter M 2011 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58 134
 Google Scholar
Google Scholar
[21] Tanter M, Fink M 2014 IEEE Trans. Ultrason. Ferroelect. Freq. Control 61 102
 Google Scholar
Google Scholar
[22] Mace E, Montaldo G, Osmanski B F, Cohen I, Fink M, Tanter M 2013 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 60 492
 Google Scholar
Google Scholar
[23] Song P F, Trzasko J D, Manduca A, Huang R Q, Kadirvel R, Kallmes D F, Chen S G 2018 IEEE Trans. Ultrason. Ferroelect. Freq. Control 65 149
 Google Scholar
Google Scholar
[24] Rachev R K, Wilcox P D, Velichko A, McAughey K L 2020 IEEE Trans. Ultrason. Ferroelect. Freq. Control 67 1303
 Google Scholar
Google Scholar
[25] Lu J Y 1998 IEEE Trans. Ultrason. Ferroelect. Freq. Control 45 84
 Google Scholar
Google Scholar
[26] Cheng J, Lu J Y 2006 IEEE Trans. Ultrason. Ferroelect. Freq. Control 53 880
 Google Scholar
Google Scholar
[27] Garcia D, Tarnec L L, Muth S, Montagnon E, Poree J, Gloutier G 2013 IEEE Trans. Ultrason. Ferroelect. Freq. Control 60 1853
 Google Scholar
Google Scholar
[28] Le Jeune L, Robert S, Prada C 2016 AIP Conference Proceedings 1706 020010
 Google Scholar
Google Scholar
[29] Rakhmatov D 2021 IEEE International Symposium on Circuits and Systems (ISCAS) Daegu, South Korea, May 22–28, 2021 p22
[30] Lukomski T 2016 Ultrasonics 70 241
 Google Scholar
Google Scholar
[31] Gazdag J 1978 Geophysics 43 1342
 Google Scholar
Google Scholar
[32] Treeby B E, Jaros J, Rohrbac D, Cox B T 2014 IEEE International Ultrasonics Symposium (IUS) Chicago, IL, Sep 03–06, 2014 p146
[33] Peralta L, Cai X, Laugier P, Grimal Q 2017 Ultrasonics 80 119
 Google Scholar
Google Scholar
[34] Li Y F, Xu K L, Li Y, Xu F, Ta D A, Wang W Q 2021 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 68 935
 Google Scholar
Google Scholar
[35] van Wijk M C, Thijssen J M 2002 Ultrasonics 40 585
 Google Scholar
Google Scholar
[36] Li H J, Le L H, Sacchi M D, Lou E H M 2013 Ultrasound Med. Biol. 39 1482
 Google Scholar
Google Scholar
[37] Merabet L, Robert S, Prada C 2019 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 66 772
 Google Scholar
Google Scholar
[38] Zhuang Z Y, Zhang J, Lian G X, Drinkwater B W 2020 Sensors 20 4951
 Google Scholar
Google Scholar
-
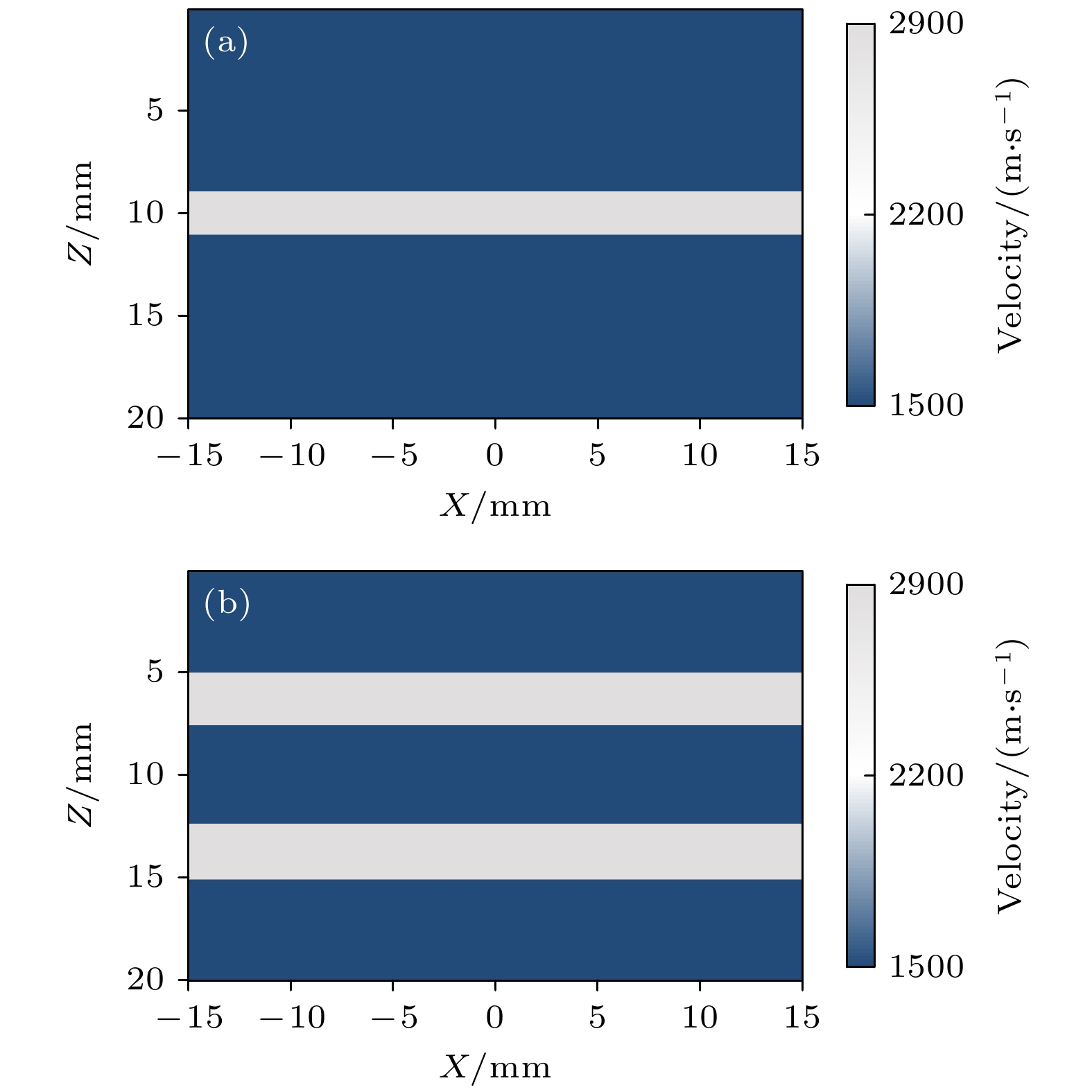
表 1 模型参数设置
Table 1. Model parameter setting.
表 2 仿真和实验设置
Table 2. Simulation and experiment setup.
设置 仿真研究 实验研究 中心频率/MHz 3.5 3.5 脉冲周期数 2 2 采样率/MHz 25 25 相邻阵元中心/mm 0.3 0.3 外推步长/mm 0.044 0.044 –6 dB带宽/MHz 2.3—4.7 2.3—4.7 阵元间距/mm 0.1 0.1 有效孔径长度/mm 38.4 38.4 网格尺寸 0.02 mm×0.02 mm — 时间步长/s 4×10–9 — 表 3 PSM-SA与PSM-PW-VI方法计算复杂度
Table 3. Computational complexity of PSM-SA and PSM-PW-VI algorithms.
操作 PSM-SA复杂度 PSM-PW-VI复杂度 2维插值 ${N_{\text{e}}}{N_x}{N_z}$ ${N_{\text{p}}}{N_x}{N_z}$ ${\mathscr{F} }_{x, t}\{\cdot\}$ $2{N_{\text{e}}}{N_{\text{t}}}{\log _2}({N_{\text{e}}}{N_{\text{t}}})$ ${N_{\text{t}}}{\log _2}({N_{\text{t}}}) + {N_{\text{p}}}{N_{\text{e}}}{\log _2}({N_{\text{e}}})$ ${\mathscr{F} }_{x}^{-1}\{\cdot\}$ $2{N_{\text{e}}}{N_x}{N_z}{\log _2}({N_x})$ ${N_{\text{p}}}{N_x}{N_z}{\log _2}({N_x})$ 表 4 PSM-SA与PSM-PW-VI方法运行时间
Table 4. Running time of PSM-SA and PSM-PW-VI imaging algorithms.
成像深度/mm PSM-SA时间/s PSM-PW-VI时间/s 7.5 158.37 8.26 25.0 208.27 9.79 -
[1] Compston J E, McClung M R, Leslie W D 2019 Lancet 393 364
 Google Scholar
Google Scholar
[2] 杨慧林 2022 中华骨与关节外科杂志 15 652
 Google Scholar
Google Scholar
Yang H L 2022 Chin. J. Bone Joint Surg. 15 652
 Google Scholar
Google Scholar
[3] Langton C M, Njeh C F 2008 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 55 1546
 Google Scholar
Google Scholar
[4] 东蕊, 刘成成, 蔡勋兵, 邵留磊, 李博艺, 他得安 2019 68 150
 Google Scholar
Google Scholar
Dong R, Liu C C, Cai X B, Shao L L, Li B Y, Ta D A 2019 Acta Phys. Sin. 68 150
 Google Scholar
Google Scholar
[5] Moilanen P, Nicholson Patrick H F, Kilappa V, Cheng, Timonen 2007 Ultrasound Med. Biol. 33 254
 Google Scholar
Google Scholar
[6] Minonzio J G, Talmant M, Laugier P 2010 J. Acoust. Soc. Am. 127 2913
 Google Scholar
Google Scholar
[7] Manes G, Tortoli P, Andreuccetti F, Avitabile G, Atzeni C 1988 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 35 14
 Google Scholar
Google Scholar
[8] Adams R B 2022 Surg. Open Sci. 10 182
 Google Scholar
Google Scholar
[9] Weismann C, Mayr C, Egger H, Auer A 2011 Breast Care 6 98
 Google Scholar
Google Scholar
[10] Zu Siederdissen C H, Potthoff A 2020 Internist 61 115
 Google Scholar
Google Scholar
[11] Nguyen Minh H, Du J, Raum K 2020 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 67 568
 Google Scholar
Google Scholar
[12] Nowicki A, Gambin B 2014 Arch. Acoust. 39 427
 Google Scholar
Google Scholar
[13] 孙宝申, 沈建中 1993 应用声学 3 43
 Google Scholar
Google Scholar
Sun B S, Shen J Z 1993 Appl. Acoust. 3 43
 Google Scholar
Google Scholar
[14] Renaud G, Kruizinga P, Cassereau D, Laugier P 2018 Phys. Med. Biol. 63 125010
 Google Scholar
Google Scholar
[15] 李云清, 江晨, 李颖, 徐峰, 许凯亮, 他得安, 黎仲勋 2019 68 184302
 Google Scholar
Google Scholar
Li Y Q, Jiang C, Li Y, Xu F, Xu K L, Ta D A, Li Z X 2019 Acta Phys. Sin. 68 184302
 Google Scholar
Google Scholar
[16] Jiang C, Li Y, Li B, Liu C, Xu F, Xu K, Ta D 2019 IEEE Access 7 163013
 Google Scholar
Google Scholar
[17] Jiang C, Li Y, Xu K L, Ta D A 2021 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 68 72
 Google Scholar
Google Scholar
[18] Li Y F, Shi Q Z, Liu Y, Gu M L, Liu C C, Song X J, Ta D A, Wang W Q 2021 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 68 2619
 Google Scholar
Google Scholar
[19] Montaldo G, Tanter M, Bercoff J, Benech N, Fink M 2009 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56 489
 Google Scholar
Google Scholar
[20] Bercoff J, Montaldo G, Loupas T, Savery D, Meziere F, Fink M, Tanter M 2011 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58 134
 Google Scholar
Google Scholar
[21] Tanter M, Fink M 2014 IEEE Trans. Ultrason. Ferroelect. Freq. Control 61 102
 Google Scholar
Google Scholar
[22] Mace E, Montaldo G, Osmanski B F, Cohen I, Fink M, Tanter M 2013 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 60 492
 Google Scholar
Google Scholar
[23] Song P F, Trzasko J D, Manduca A, Huang R Q, Kadirvel R, Kallmes D F, Chen S G 2018 IEEE Trans. Ultrason. Ferroelect. Freq. Control 65 149
 Google Scholar
Google Scholar
[24] Rachev R K, Wilcox P D, Velichko A, McAughey K L 2020 IEEE Trans. Ultrason. Ferroelect. Freq. Control 67 1303
 Google Scholar
Google Scholar
[25] Lu J Y 1998 IEEE Trans. Ultrason. Ferroelect. Freq. Control 45 84
 Google Scholar
Google Scholar
[26] Cheng J, Lu J Y 2006 IEEE Trans. Ultrason. Ferroelect. Freq. Control 53 880
 Google Scholar
Google Scholar
[27] Garcia D, Tarnec L L, Muth S, Montagnon E, Poree J, Gloutier G 2013 IEEE Trans. Ultrason. Ferroelect. Freq. Control 60 1853
 Google Scholar
Google Scholar
[28] Le Jeune L, Robert S, Prada C 2016 AIP Conference Proceedings 1706 020010
 Google Scholar
Google Scholar
[29] Rakhmatov D 2021 IEEE International Symposium on Circuits and Systems (ISCAS) Daegu, South Korea, May 22–28, 2021 p22
[30] Lukomski T 2016 Ultrasonics 70 241
 Google Scholar
Google Scholar
[31] Gazdag J 1978 Geophysics 43 1342
 Google Scholar
Google Scholar
[32] Treeby B E, Jaros J, Rohrbac D, Cox B T 2014 IEEE International Ultrasonics Symposium (IUS) Chicago, IL, Sep 03–06, 2014 p146
[33] Peralta L, Cai X, Laugier P, Grimal Q 2017 Ultrasonics 80 119
 Google Scholar
Google Scholar
[34] Li Y F, Xu K L, Li Y, Xu F, Ta D A, Wang W Q 2021 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 68 935
 Google Scholar
Google Scholar
[35] van Wijk M C, Thijssen J M 2002 Ultrasonics 40 585
 Google Scholar
Google Scholar
[36] Li H J, Le L H, Sacchi M D, Lou E H M 2013 Ultrasound Med. Biol. 39 1482
 Google Scholar
Google Scholar
[37] Merabet L, Robert S, Prada C 2019 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 66 772
 Google Scholar
Google Scholar
[38] Zhuang Z Y, Zhang J, Lian G X, Drinkwater B W 2020 Sensors 20 4951
 Google Scholar
Google Scholar
计量
- 文章访问数: 6414
- PDF下载量: 126
- 被引次数: 0













 下载:
下载: