-
数字全息技术是目前应用最广泛的定量相位成像技术之一, 但是当测量相位较大的物体时, 需要解包裹算法才能计算出正确的相位信息. 目前, 已有的解包裹算法均面临计算量巨大、耗时的问题. 为了解决上述问题, 本文基于傅里叶变换相位恢复算法, 利用复振幅相位信息的完整性, 提出针对薄相位和连续大相位的基于数字差分-积分的快速直接解包裹算法. 该算法首先通过基本的傅里叶变换相位恢复算法操作后, 得到含有物体完整相位的复振幅信息; 随后, 从中提取两幅子复振幅信息, 并将二者相除, 再相位提取出其中信息, 便可得到一个物体真实相位差分信息; 最后, 沿差分方向对提取的相位差分信息进行积分, 便可得到解包裹后的相位信息. 同时通过仿真与具体实验对该算法进行了验证. 结果表明, 本文算法可以实现快速准确的解包裹相位直接恢复.Digital holography is one of the most widely used quantitative phase imaging technologies at present, owing to its non-contact, high-accuracy and full-filed measurement. However, when the optical path difference induced by the measurement sample is larger than the used wavelength, a phase unwrapping algorithm has to be utilized to unwrap the phase and retrieve the actual phase. And the existing phase unwrapping algorithms suffer huge computational burden and slow retrieval speed. Although they have been greatly improved, their retrieval speed is limited by the phase unwrapping. In order to solve the above-mentioned problems, a digital differentiation-integration based phase unwrapping is proposed in this paper. This algorithm is based on the fact that the actual phase information is contained in the complex-valued function after Fourier transform, band-pass filter and inverse Fourier transform. After Fourier transform, band-pass filter and inverse Fourier transform, a complex-valued function containing the actual phase is retrieved, and two sub complex-valued functions can be extracted with just one-pixel shift digitally. Then, two functions are divided pixel by pixel, and another complex-valued function containing the differentiation of the actual phase is obtained. So the differential phase can be retrieved easily by the phase extraction. Finally, the retrieved differential phase is integrated along the inverse direction of shifting, and the unwrapped phase can be obtained directly. This algorithm can work effectively when the variation of the measurement phase is in a range of (–π, π]. This algorithm is just based on the Fourier transform and the complex-valued division. Unlike the existing unwrapping algorithms, this algorithm is much easier to conduct and has light computation burden. Therefore, this algorithm can realize fast and accurate phase reconstruction directly. Several simulation and experimental results can verify the effectiveness of this algorithm.
-
Keywords:
- off-axis digital holography /
- phase retrieval /
- Fourier transform /
- phase unwrapping
[1] Popescu G, Ikeda T, Dasari R R, Feld M S 2006 Opt. Lett. 31 775
Google Scholar
[2] Du Y Z, Feng G Y, Li H R, Vargas J, Zhou S H 2012 Opt. Lett. 37 3927
Google Scholar
[3] Shaked N T 2012 Opt. Lett. 37 2016
Google Scholar
[4] Gabai H, Baranes-Zeevi M, Zilberman M, Shaked N T 2013 Opt. Lett. 38 3017
Google Scholar
[5] Girshovitz P, Shaked N T 2014 Light Sci. Appl. 3 e151
Google Scholar
[6] Mahajan S, Trivedi V, Vora P, Chhaniwal V, Javidi B, Anand A 2015 Opt. Lett. 40 3743
Google Scholar
[7] Nativ A, Shaked N T 2017 Opt. Lett. 42 1492
Google Scholar
[8] Jiao Y H, Kandel M E, Liu X J, Lu W L, Popescu G 2020 Opt. Express 28 34190
Google Scholar
[9] Rajput S K, Matoba O, Kumar M, Quan X Y, Awatsuji Y 2021 Opt. Las. Eng. 137 106331
Google Scholar
[10] Zhang J W, Dai S Q, Ma C J, Xi T L, Di J L, Zhao J L 2021 Light Adv. Manuf. 2 333
Google Scholar
[11] Barojas-Gutierrez E, Flores-Meneses C, Meneses-Fabian C 2023 Opt. Las. Tech. 157 108691
Google Scholar
[12] Pham H V, Edwards C, Goddard L V, Popescu G 2013 Appl. Opt. 52 A97
Google Scholar
[13] Hao B G, Shan M G, Zhong Z, Diao M, Wang Y, Zhang Y B 2015 J. Opt. 17 035602
Google Scholar
[14] Gao P, Harder I, Nercissian V, Mantel K, Yao B L 2010 Opt. Lett. 35 712
Google Scholar
[15] Bai H Y, Shan M G, Zhong Z, Guo L L, Zhang Y B 2015 Opt. Las. Eng.75 1
Google Scholar
[16] Bai H Y, Shan M G, Zhong Z, Guo L L, Zhang Y B 2015 Appl. Opt. 54 9513
Google Scholar
[17] Huang Z Z, Memmolo P, Ferraro P, Cao L C 2022 PhotoniX 3 3
Google Scholar
[18] 钟志, 赵婉婷, 单明广, 刘磊 2021 70 154202
Google Scholar
Zhong Z, Zhao W T, Shan M G, Liu L 2021 Acta Phys. Sin. 70 154202
Google Scholar
[19] Ma L H, Li Y, Wang H, Jin H Z 2012 Appl. Opt. 51 8800
Google Scholar
[20] Arevalillo-Herráez M, Villatoro F, Gdeisat M 2016 IEEE T. Image Process. 25 2601
Google Scholar
[21] de Souza J C, Oliveira M E, dos Santos P A M 2015 Opt. Lett. 40 3456
Google Scholar
[22] Pritt M D, Shipman J S 1994 IEEE T. Geosci. Remote 32 706
Google Scholar
[23] Li B Y, Tang C, Zhou Q L, Lei Z K 2019 Appl. Opt. 58 219
Google Scholar
[24] Wei C, Ma J, Miao X Y, Wang N F, Zong Y, Yuan C J 2022 Opt. Express 30 1686
Google Scholar
[25] Spoorthi G E, Gorthi R K S S, Gorthi S 2020 IEEE T. Image Process. 29 4862
Google Scholar
[26] Wang K Q, Qian K M, Di J L, Zhao J L 2022 Adv. Photonics Nexus 1 014001
Google Scholar
[27] Xu M, Tang C, Shen Y X, Hong N, Lei Z K 2022 Opt. Las. Eng. 151 106824
Google Scholar
[28] Zhong Z, Wang C, Liu L, Yu L, Shan M G 2022 J. Mod. Optics 69 219
Google Scholar
-
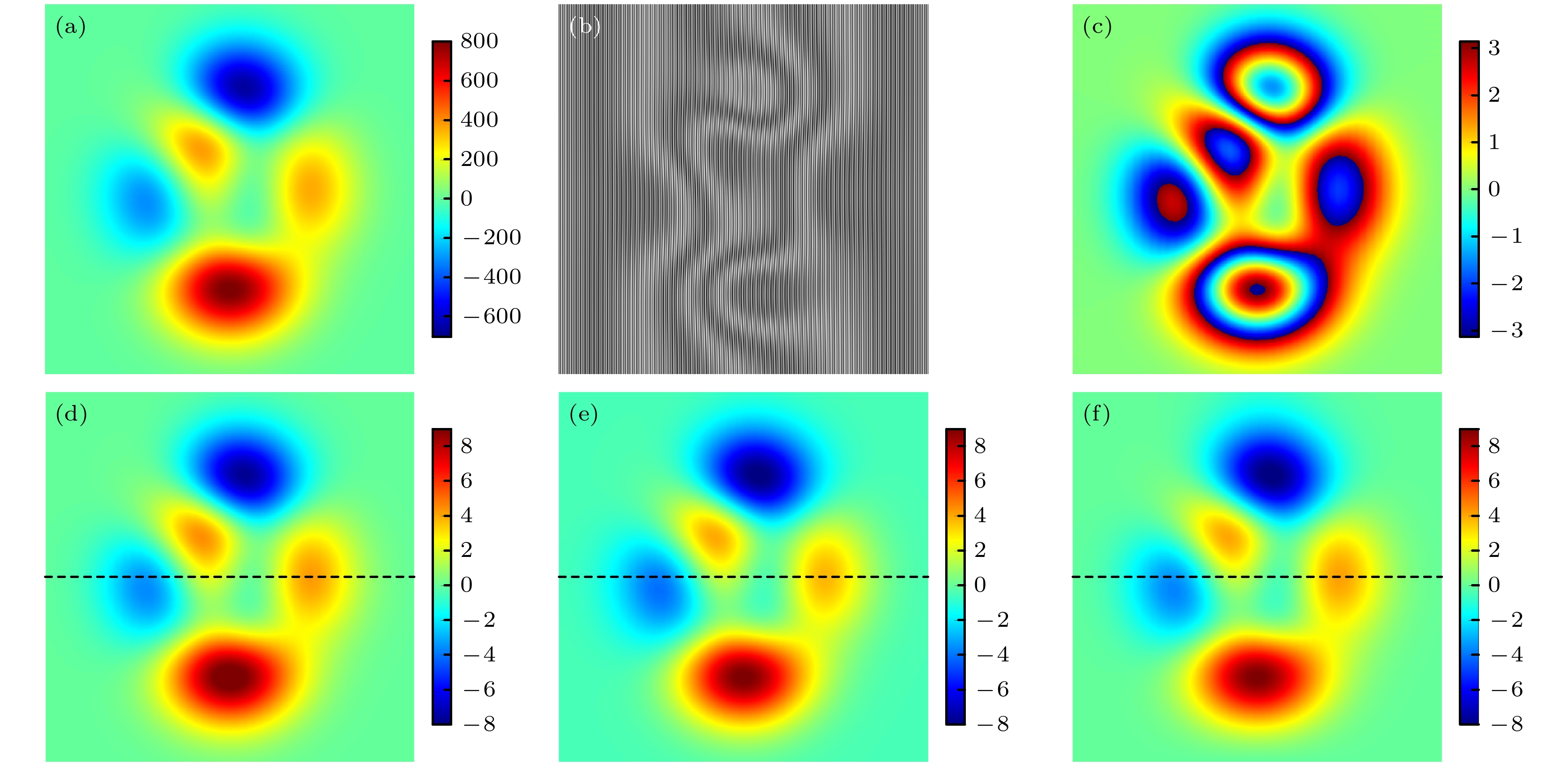
图 2 (a) Peak值相位型物体及其(b)离轴全息图; (c)傅里叶变换法的恢复结果; 使用(d)枝切法和 (e)最小二乘法的解包裹结果; (f)本文所提算法的恢复结果
Fig. 2. (a) Phase object with peak values and (b) its off-axis hologram; (c) the retrieved result of the Fourier transform; the unwrapped results by (d) branch-cut and (e) least square; (f) the retrieved result of this proposed algorithm.
Fig. 3. One-dimensional (1D) phase profile along the black dashed lines in Figs. 2 (d)—(f).
图 4 (a) 全息图; (b)傅里叶变换法恢复结果; (c)本文算法恢复结果
Fig. 4. (a) A hologram; (b) the retrieved result by Fourier transform; (c) the retrieved result by the proposed algorithm.
图 6 (a) 全息图; 使用(b)枝切法和(c)最小二乘的恢复结果; (d)本文算法恢复结果
Fig. 6. (a) A hologram; the retrieved results by (b) branch-cut and (c) least square; (d) the retrieved results by the proposed algorithm.
Fig. 7. 1D phase profile along the black dashed lines in Fig. 6 (b)-(d).
表 1 三种算法比较
Table 1. Comparison of three algorithms.
时间/s 256 ×256 512×512 1024×1024 枝切法 0.0223 0.0850 0.3744 最小二乘法 0.0069 0.0242 0.0798 本文算法 0.0031 0.0087 0.0293 
下载: 导出CSV
-
[1] Popescu G, Ikeda T, Dasari R R, Feld M S 2006 Opt. Lett. 31 775
Google Scholar
[2] Du Y Z, Feng G Y, Li H R, Vargas J, Zhou S H 2012 Opt. Lett. 37 3927
Google Scholar
[3] Shaked N T 2012 Opt. Lett. 37 2016
Google Scholar
[4] Gabai H, Baranes-Zeevi M, Zilberman M, Shaked N T 2013 Opt. Lett. 38 3017
Google Scholar
[5] Girshovitz P, Shaked N T 2014 Light Sci. Appl. 3 e151
Google Scholar
[6] Mahajan S, Trivedi V, Vora P, Chhaniwal V, Javidi B, Anand A 2015 Opt. Lett. 40 3743
Google Scholar
[7] Nativ A, Shaked N T 2017 Opt. Lett. 42 1492
Google Scholar
[8] Jiao Y H, Kandel M E, Liu X J, Lu W L, Popescu G 2020 Opt. Express 28 34190
Google Scholar
[9] Rajput S K, Matoba O, Kumar M, Quan X Y, Awatsuji Y 2021 Opt. Las. Eng. 137 106331
Google Scholar
[10] Zhang J W, Dai S Q, Ma C J, Xi T L, Di J L, Zhao J L 2021 Light Adv. Manuf. 2 333
Google Scholar
[11] Barojas-Gutierrez E, Flores-Meneses C, Meneses-Fabian C 2023 Opt. Las. Tech. 157 108691
Google Scholar
[12] Pham H V, Edwards C, Goddard L V, Popescu G 2013 Appl. Opt. 52 A97
Google Scholar
[13] Hao B G, Shan M G, Zhong Z, Diao M, Wang Y, Zhang Y B 2015 J. Opt. 17 035602
Google Scholar
[14] Gao P, Harder I, Nercissian V, Mantel K, Yao B L 2010 Opt. Lett. 35 712
Google Scholar
[15] Bai H Y, Shan M G, Zhong Z, Guo L L, Zhang Y B 2015 Opt. Las. Eng.75 1
Google Scholar
[16] Bai H Y, Shan M G, Zhong Z, Guo L L, Zhang Y B 2015 Appl. Opt. 54 9513
Google Scholar
[17] Huang Z Z, Memmolo P, Ferraro P, Cao L C 2022 PhotoniX 3 3
Google Scholar
[18] 钟志, 赵婉婷, 单明广, 刘磊 2021 70 154202
Google Scholar
Zhong Z, Zhao W T, Shan M G, Liu L 2021 Acta Phys. Sin. 70 154202
Google Scholar
[19] Ma L H, Li Y, Wang H, Jin H Z 2012 Appl. Opt. 51 8800
Google Scholar
[20] Arevalillo-Herráez M, Villatoro F, Gdeisat M 2016 IEEE T. Image Process. 25 2601
Google Scholar
[21] de Souza J C, Oliveira M E, dos Santos P A M 2015 Opt. Lett. 40 3456
Google Scholar
[22] Pritt M D, Shipman J S 1994 IEEE T. Geosci. Remote 32 706
Google Scholar
[23] Li B Y, Tang C, Zhou Q L, Lei Z K 2019 Appl. Opt. 58 219
Google Scholar
[24] Wei C, Ma J, Miao X Y, Wang N F, Zong Y, Yuan C J 2022 Opt. Express 30 1686
Google Scholar
[25] Spoorthi G E, Gorthi R K S S, Gorthi S 2020 IEEE T. Image Process. 29 4862
Google Scholar
[26] Wang K Q, Qian K M, Di J L, Zhao J L 2022 Adv. Photonics Nexus 1 014001
Google Scholar
[27] Xu M, Tang C, Shen Y X, Hong N, Lei Z K 2022 Opt. Las. Eng. 151 106824
Google Scholar
[28] Zhong Z, Wang C, Liu L, Yu L, Shan M G 2022 J. Mod. Optics 69 219
Google Scholar
下载:
计量
- 文章访问数: 2625
- PDF下载量: 66
- 被引次数: 0
