-
现有均匀场往往基于阵列天线的特殊排布, 通过平顶波束赋形在角远场区域或者通过点聚焦在近场区域生成的, 生成的均匀场直接受制于阵列排布形态且无法灵活调控. 提出了一种基于角谱域和改进时间反演方法相结合的均匀场生成方法, 该方法不受阵列排布的限制, 能够以同一阵列排布形态, 在包括近场区域在内的任意位置, 生成指定大小、形状以及偏转角度的多种均匀场. 首先理论解析了本方法不受阵列排布限制的原因; 其次数值验证了固定阵列排布形态灵活生成多种均匀场的能力; 最后引入时间反演方法, 并做出反演信号幅度倒数加权的改进, 解决了上述均匀场在生成过程中由幅度衰减和相位延迟带来均匀场平坦度恶化等问题. 研究结果表明, 合成场质量与其对应角谱域包络的主瓣和副瓣信息有关, 且生成任意均匀场必须包含至少1/2的角谱域主瓣信息和1/2的副瓣信息. 本方法能够灵活调控一维和二维均匀场的位置、大小、形状以及偏转角度, 为灵活生成均匀场提供了一条新思路.Existing uniform fields are usually based on the special arrangement of the array antenna. The uniform fields generated by flat-top beam shaping in angular far-field area or by point focusing in near-field area are directly subject to the array configuration and cannot be flexibly controlled. This paper presents a method of generating uniform field based on the combination of angular spectral domain and improved time reversal technique. This method is not limited by the array arrangement. It can generate a uniform field of specified size, shape and deflection angle in the same array arrangement at any position, including the near-field region. In this work, the reason why this method is not limited by array arrangement is explained theoretically. Secondly, the ability of the fixed array configuration to generate multiple uniform fields is validated numerically. Finally, the time-reversal technique of reversal signal amplitude reciprocal weighting is introduced. The problem of deterioration of uniform field flatness, caused by amplitude decay and phase delay during the generation of uniform field, is solved through this technology. The results show that the quality of the synthesized field is related to the main lobe and sidelobe information of its corresponding angular spectrum domain envelope, and the generated any uniform field must contain at least half of the angular spectrum domain main lobe information and half of the sidelobe information. This method can flexibly control the position, size, shape and deflection angle of one-dimensional and two-dimensional uniform field, which provides a new way to flexibly generating uniform fields.
-
Keywords:
- angular spectrum domain /
- time reversal /
- uniform field
[1] Qi Y H, Yang G, Liu L, Fan J, Antonio O, Kong H W, Yu W, Yang Z P 2017 IEEE Trans. Electromagn. Compat. 59 1661
Google Scholar
[2] 毕欣, 黄林, 杜劲松, 齐伟智, 高扬, 荣健, 蒋华北 2015 64 014301
Google Scholar
Bi X, Huang L, Du J S, Qi W Z, Gao Y, Rong J, Jiang H B 2015 Acta Phys. Sin. 64 014301
Google Scholar
[3] Seong H A, Chang H J, Dong M L, Wang S L 2020 IEEE Trans. Microwave Theory Tech. 68 2867
Google Scholar
[4] Yang Y, Fan Z P, Hong T, Chen M S, Tang X W, He J B, Chen X, Liu C J, Zhu H C, Huang K 2020 IEEE Trans. Microwave. Theory Tech. 68 4896
Google Scholar
[5] Giulio M B, Sara A, Gaetano M 2020 IEEE Trans. Antennas Propag. 68 6906
Google Scholar
[6] Wang J, Zheng Y N, He Z Y 2015 Antenna Array Theory and Engineering Applications (Vol. 1) (Beijing: Publishing House of Electronics Industry) pp93–101 (in Chines) [王建, 郑一农, 何子远 2015 阵列天线理论与工程应用 (北京: 电子工业出版社) 第93—101页
Wang J, Zheng Y N, He Z Y 2015 Antenna Array Theory and Engineering Applications (Vol. 1) (Beijing: Publishing House of Electronics Industry) pp93–101 (in Chines) [7] Li J Y, Qi Y X, Zhou S G 2017 IEEE Trans. Antennas Propag. 65 6157
Google Scholar
[8] Rao K S, Chakraborty A, Das B 1986 Antennas & Propagation Society International Symposium Philadelphia, PA, USA, June 08–13, 1986 p387
[9] Liu Y H, Liu Q H, Nie Z P 2010 IEEE Trans. Antennas Propag. 58 604
Google Scholar
[10] Shen H O, Wang B H, Li X 2017 IEEE Trans. Antennas Propag. 16 1098
Google Scholar
[11] Gu P F, Wang G, Fan Z H, Chen R S 2019 IEEE Trans. Antennas Propag. 67 7320
Google Scholar
[12] 张金玲, 万文钢, 郑占奇, 甘曦, 朱兴宇 2015 64 110504
Google Scholar
Zhang J L, Wen W G, Zheng Z Q, Gan X, Zhu X Y 2015 Acta Phys. Sin. 64 110504
Google Scholar
[13] Francisco J A P, Juan A R G, Emilio V L, S R R 1999 IEEE Trans. Antennas Propag. 47 506
Google Scholar
[14] Bitan M, G K Mahanti 2021 6th International Conference on Communication and Electronics Systems (ICCES) Coimbatre, India, July 8–10, 2021 p447
[15] Guo S, Zhao D S, Wang B Z 2022 IEEE Trans. Antennas Propag. 21 908
Google Scholar
[16] Elsa D T, Juan M C, Alejandro D M 2007 IEEE Trans. Microwave Theory Tech. 55 85
Google Scholar
[17] Kumari V, Ahmed A, Kanumuri T, Shakher C, Sheoran G 2020 Int. J. Imaging Syst. Technol. 30 391
Google Scholar
[18] 安腾远, 丁霄, 王秉中 2023 72 030401
Google Scholar
An T Y, Ding X, Wang B Z 2023 Acta Phys. Sin. 72 030401
Google Scholar
[19] Zhao D S, Zhu M 2016 IEEE Antennas Wireless Propag. Lett. 15 1739
Google Scholar
[20] 王秉中, 王任 2020 时间反演电磁学 (北京: 科学出版社 第165—179页
Wang B Z, Wang R 2020 Time Reversal Electromagnetism (Beijing: Science Press) pp165–179
[21] 臧锐, 王秉中, 丁帅, 龚志双 2016 65 204102
Google Scholar
Zang R, Wang B Z, Ding S, Gong Z S 2016 Acta Phys. Sin. 65 204102
Google Scholar
[22] 张知原, 李冰, 刘仕奇, 张洪林, 胡斌杰, 赵德双, 王楚楠 2022 71 014101
Google Scholar
Zhang Z Y, Li B, Liu S Q, Zhang H L, Hu B J, Zhao D S, Wang C N 2022 Acta Phys. Sin. 71 014101
Google Scholar
[23] Guo S, Zhao D S, Wang B Z, Cao W P 2020 IEEE Trans. Antennas Propag. 68 8249
Google Scholar
[24] Chen Z W, Liang F, Zhang Q L, Li B, Ge G D, Zhao D S 2021 IEEE Trans. Antennas Propag. 69 7011
Google Scholar
-
图 2 三种不同阵列排布对应的角谱域采样图和合成场分布图 (a)归一化角谱域采样图; (b)归一化电场分布图
Fig. 2. Angular spectrum domain sampling diagram and synthetic field distribution diagram of three different array configurations: (a) Normalized angular spectrum domain sampling diagram; (b) normalized electric field distribution diagram.
图 3 改变阵元数量后的角谱域和合成场 (a)阵元间距为0.5λ的角谱域采样结果; (b)不同阵元数量的阵列在目标位置的合成场
Fig. 3. Angular spectrum domain and generated field after changing number of array elements: (a) Angular spectrum domain sampling results with a spacing of 0.5λ between array elements; (b) composite field of arrays with different number of array elements at target position.
图 4 两阵列和目标均匀场的空间分布 (a)等空域直线阵列 (b)非均匀直线阵列
Fig. 4. Spatial distribution of two arrays and target uniform field: (a) Isospatial linear array; (b) non-uniform linear array.
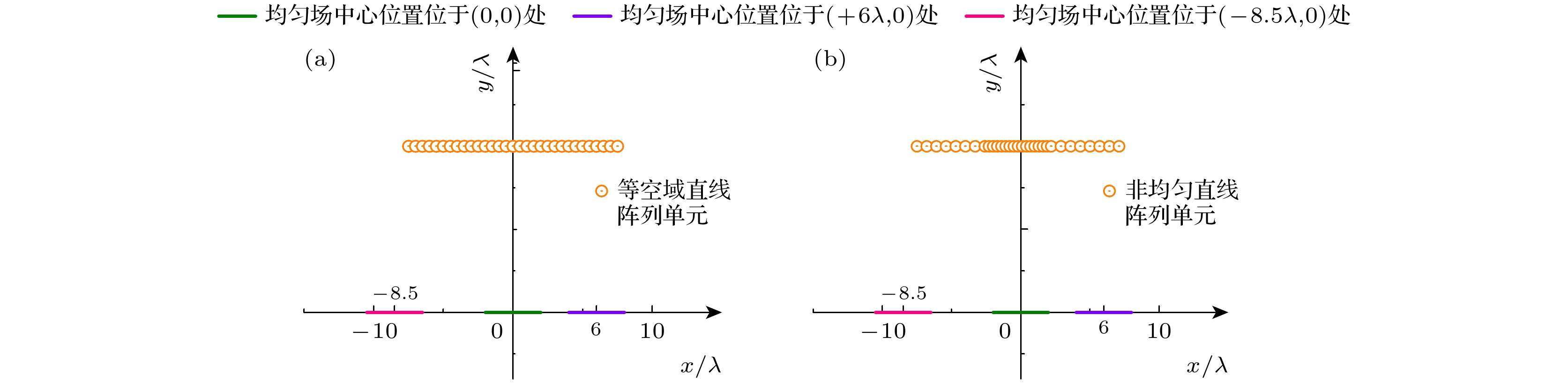
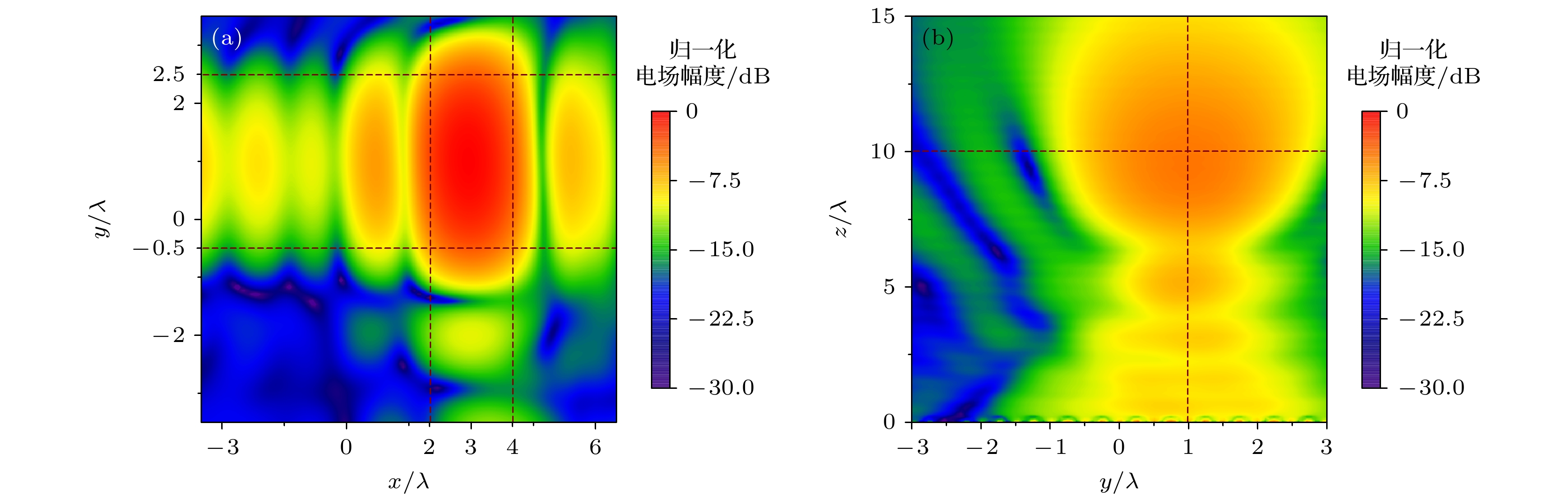
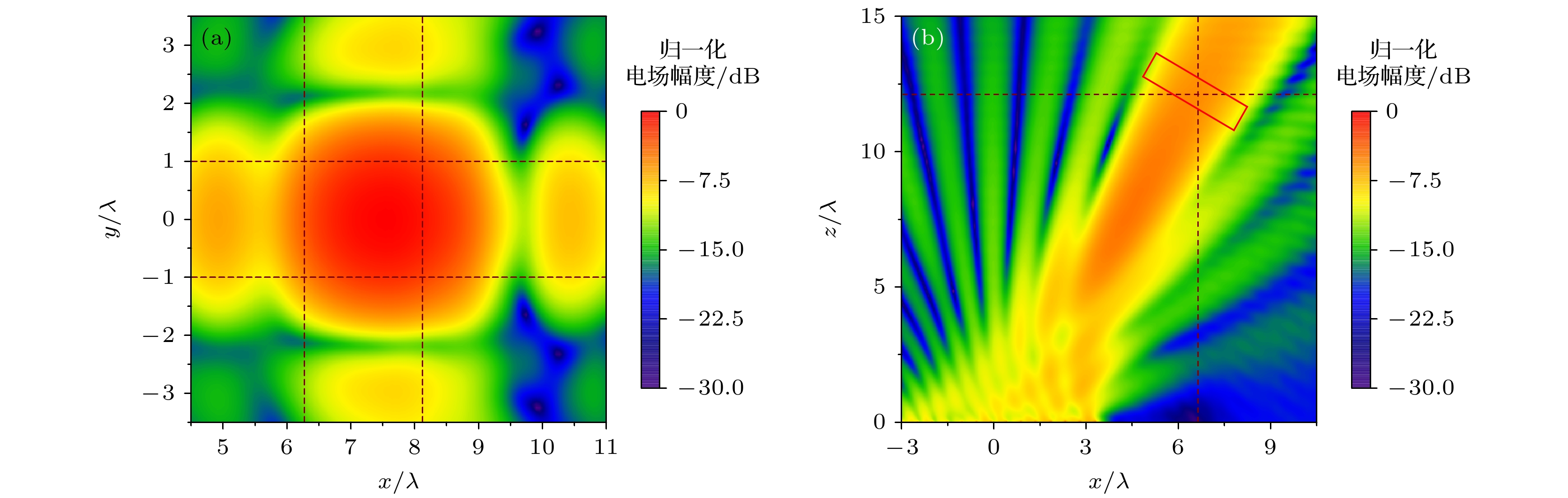
图 5 目标均匀场对应的角谱域采样图和合成场分布图 (a)等空域直线阵列归一化角谱域采样图; (b)等空域直线阵列归一化电场分布图; (c)非均匀直线阵列归一化角谱域采样图; (d)非均匀直线阵列归一化电场分布图
Fig. 5. Angular spectrum domain sampling diagram and composite field distribution diagram of uniform field: (a) Normalized angular spectrum domain sampling diagram for isospatial linear array; (b) normalized electric field distribution diagram for isospatial linear array; (c) normalized angular spectrum domain sampling diagram for non-uniform linear array; (d) normalized electric field distribution diagram for non-uniform linear array.
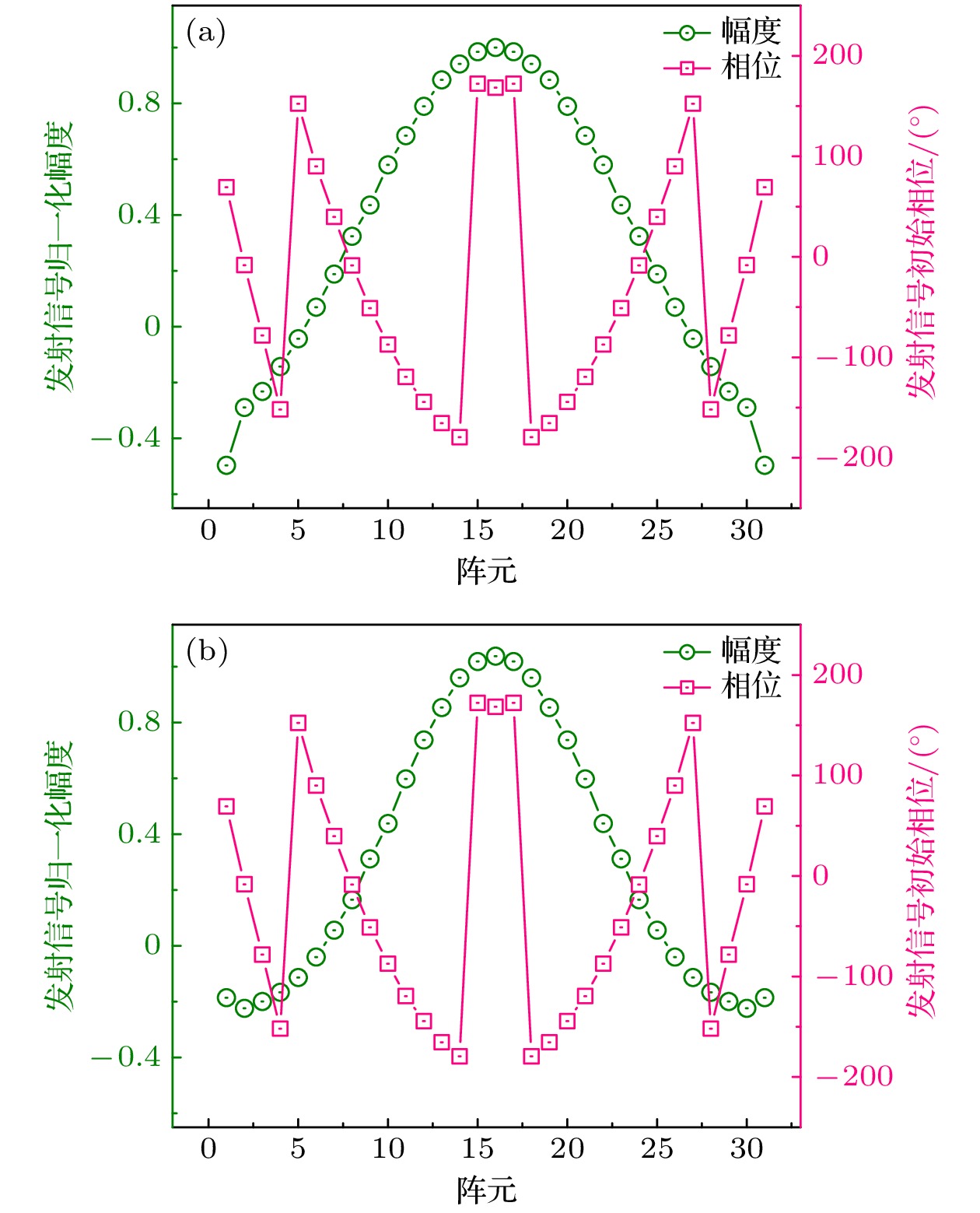
图 6 各个阵元对应的归一化角频率 (a)目标均匀场位于(0λ, 0λ); (b) 目标均匀场位于(0λ, –5λ); (c) 目标均匀场位于(–5λ, –5λ)
Fig. 6. Normalized angular frequency corresponding to each array element: (a) Target uniform field is located at (0λ, 0λ); (b) target uniform field is located at (0λ, –5λ); (c) target uniform field is located at (–5λ, –5λ).
图 7 幅度归一化合成场 (a)目标均匀场位于(0λ, 0λ); (b) 目标均匀场位于(0λ, –5λ); (c) 目标均匀场位于(–5λ, –5λ)
Fig. 7. Amplitude normalization field: (a) Target uniform field is located at (0λ, 0λ); (b) target uniform field is located at (0λ, –5λ); (c) target uniform field is located at (–5λ, –5λ).
图 8 各阵元辐射能量的幅度和初始相位 (a)本文提出的改进时间反演方法; (b)传统的时间反演方法
Fig. 8. Amplitude and initial phase of radiation energy of each array element: (a) Improved time reversal method proposed in this paper; (b) traditional time reversal method.
图 9 两种时间反演方法在目标位置的合成场对比
Fig. 9. Comparison of two time reversal methods in synthetic field of target location.
图 10 用于合成目标均匀微波场的等空域直线阵列
Fig. 10. Isospatial linear array for synthesizing uniform microwave field of target.
图 11 电场分布图 (a)目标场1; (b)目标场2; (c)目标场3; (d)目标场4; (e)目标场5
Fig. 11. Electric field distributions: (a) Target field 1; (b) target field 2; (c) target field 3; (d) target field 4; (e) target field 5.
图 12 用于合成目标均匀微波场的均匀栅格平面阵
Fig. 12. Uniform raster planar array for synthesizing uniform microwave field of target.
表 1 5个目标场对应的空域、角谱域表达式以及各阵元的投影夹角
Table 1. Five target field expression spatial domain, spatial frequency domain and projection angle of each element.
目标场 空域表达式 角谱域表达式 θn 1 $ E(x, 15\lambda ) = \left\{ {\begin{aligned} &{1, \;\;|x| \leqslant 1.5\lambda } \\ &{0, \;\;{\text{others}}}\end{aligned}} \right. $ $\widetilde{E} ({k_x}) = 2\dfrac{{\sin (3{k_x}\lambda /2)}}{{{k_x}}}$ ${\theta _n} = {\rm{arccos}}\left( {\dfrac{{(n - 16)\lambda /2}}{{\sqrt {{{\left[ {(n - 16)\lambda /2} \right]}^2} + {{\left( {15\lambda } \right)}^2}} }}} \right)$ 2 $E(x, 10\lambda ) = \left\{ {\begin{aligned} &{1, \;\;{{ - 3}}\lambda < x < \lambda } \\ &{0, \;\;{\text{others}}}\end{aligned}} \right.$ $\widetilde{E} ({k_x}) = 2\dfrac{{\sin (2{k_x}\lambda /2)}}{{{k_x}}}$ $ {\theta _n} = {\rm{arccos}}\left( {\dfrac{{(n - 16)\lambda /2 + 2\lambda }}{{\sqrt {{{\left[ {(n - 16)\lambda /2 + 2\lambda } \right]}^2} + {{\left( {10\lambda } \right)}^2}} }}} \right) $ 3 $ E(x, 10\lambda ) = \left\{ {\begin{aligned} &1 , \;\;{ - 3\lambda \leqslant x \leqslant - \lambda }\\ &{1, }\;\;{\lambda \leqslant x \leqslant 3\lambda {\text{ }}} \\ &{0, }\;\;{{\text{others }}}\end{aligned}} \right. $ $\widetilde{E} ({k_x}) = 2\dfrac{{\sin (3{k_x}\lambda /2) - \sin ({k_x}\lambda /2)}}{{{k_x}}}$ ${\theta _n} = {\rm{arccos}}\left( {\dfrac{{(n - 16)\lambda /2}}{{\sqrt {{{\left[ {(n - 16)\lambda /2} \right]}^2} + {{\left( {10\lambda } \right)}^2}} }}} \right)$ 4 $ E(x, y) = \left\{ {\begin{aligned} &{1,\;\; y = x + 13\lambda , {\text{ }}} \\ & ~~~- 3 - \dfrac{{\sqrt 2 }}{2} < \dfrac{x}{\lambda} < - 3 + \dfrac{{\sqrt 2 }}{2};\\ &0, \;\;{\text{others}} \end{aligned}} \right. $ $\widetilde{E} ({k_x}) = 2\dfrac{{\sin (2{k_x}\lambda /2)}}{{{k_x}}}$ ${\theta _n} = {\rm{arccos}}\left( {\dfrac{{(n - 16)\lambda /2 + 3\lambda }}{{\sqrt {{{\left[ {(n - 16)\lambda /2 + 3\lambda } \right]}^2} + {{\left( {10\lambda } \right)}^2}} }}} \right) + \dfrac{{\text{π }}}{4}$ 5 $ E(x, y) = \left\{ {\begin{aligned}& 1, \;\; y = x + 17.5\lambda ,\\ & ~~~- 8.5\lambda < x < - 6.5\lambda; \\ &0,\;\; {\text{others}} \end{aligned}} \right. $ $\widetilde{E} ({k_x}) = 2\dfrac{{\sin (2\sqrt 2 {k_x}\lambda /2)}}{{{k_x}}}$ ${\theta _n} = {\rm{arccos}}\left( {\dfrac{{(n - 16)\lambda /2 + 7.5\lambda }}{{\sqrt {{{\left[ {(n - 16)\lambda /2 + 7.5\lambda } \right]}^2} + {{\left( {10\lambda } \right)}^2}} }}} \right) + \dfrac{{\text{π }}}{4}$ 
下载: 导出CSV
表 2 3个目标场对应的空域、角谱域表达式
Table 2. Three target field expression spatial domain, spatial frequency domain.
目标场 空域表达式 角谱域表达式 1 $ E(x, y, 10\lambda ) = \left\{ \begin{aligned} &{1, }\;\;{\left| x \right| \leqslant \lambda , \left| y \right| \leqslant \lambda } \\ & {0, }\;\;{{\text{others }}} \end{aligned} \right. $ $\widetilde E ({k_x}, {k_y}) = 4\dfrac{{\sin (2{k_x}\lambda /2)}}{{{k_x}}} \cdot \dfrac{{\sin (2{k_y}\lambda /2)}}{{{k_y}}}$ 2 $ E(x, y, 10\lambda ) = \left\{ {\begin{aligned} &{1, }\;\;{\begin{aligned} &{2\lambda \leqslant x \leqslant 4\lambda {\text{ }}} \\ &{ - 0.5\lambda \leqslant y \leqslant 2.5\lambda } \end{aligned}} \\ & {0, }\;\;{{\text{others }}} \end{aligned}} \right. $ $\widetilde E ({k_x}, {k_y}) = 4\dfrac{{\sin (2{k_x}\lambda /2)}}{{{k_x}}} \cdot \dfrac{{\sin (3{k_y}\lambda /2)}}{{{k_y}}}$ 3 $ E(x, y, z) = \left\{ \begin{aligned} &{1, }\;\;{\begin{aligned} &{\sqrt 3 z = - x + 28\lambda } \\ &{6\lambda \leqslant x \leqslant 8\lambda } \\ & { - \lambda \leqslant y \leqslant \lambda {\text{ }}} \end{aligned}} \\ & {0, }\;\;{{\text{others }}} \end{aligned} \right.$ $\widetilde E ({k_x}, {k_y}) = 4\dfrac{{\sin (2{k_x}\lambda /2)}}{{{k_x}}} \cdot \dfrac{{\sin (2{k_y}\lambda /2)}}{{{k_y}}}$
下载: 导出CSV
表 3 3个目标场对应的各阵元的投影夹角
Table 3. Three target field projection angle of each element.
目标场 θn φn 1 $ {\rm{ arcsin}}\left( {\dfrac{{\sqrt {{{[({n_x} - 11)\lambda /2]}^2} + {{[({n_y} - 11)\lambda /2]}^2}} }}{{\sqrt {{{[({n_x} - 11)\lambda /2]}^2} + {{[({n_y} - 11)\lambda /2]}^2} + {{\left( {10\lambda } \right)}^2}} }}} \right) $ ${\rm{ arctan}}\left( {\dfrac{{({n_x} - 6)\lambda /2}}{{({n_y} - 6)\lambda /2}}} \right)$ 2 $ {\rm{ arcsin}}\left( {\dfrac{{\sqrt {{{\left[ {({n_x} - 6)\lambda /2 - 3\lambda } \right]}^2} + {{\left[ {({n_y} - 6)\lambda /2 - \lambda } \right]}^2}} }}{{\sqrt {{{\left[ {({n_x} - 6)\lambda /2 - 3\lambda } \right]}^2} + {{\left[ {({n_y} - 6)\lambda /2 - \lambda } \right]}^2} + {{\left( {10\lambda } \right)}^2}} }}} \right) $ $ {\rm{ arctan}}\left( {\dfrac{{({n_x} - 11)\lambda /2 - 3\lambda }}{{({n_y} - 11)\lambda /2 - \lambda }}} \right) $ 3 ${\rm{ arcsin}}\left( {\dfrac{{\sqrt {{\text{d}}{x_n^2} + {{\left[ {({n_y} - 11)\lambda /2} \right]}^2}} }}{{\sqrt {{\text{d}}{x_n^2} + {{\left[ {({n_y} - 11)\lambda /2} \right]}^2} + {\text{d}}{z_n^2}} }}} \right) ^*$ ${\rm{ arctan}}\left( {\dfrac{{{\text{d}}{x_n}}}{{({n_y} - 11)\lambda /2}}} \right) ^*$ 注: *其中 $ {\text{d}}{x_n} = \dfrac{{{{\left[ {\dfrac{{\left( {{n_x} - 11} \right)\lambda /2}}{{\cos ({\text{π }}/6)}}} \right]}^2} + \bigg\{ {{\left( {7\sqrt 3 \lambda } \right)}^2} + {{\left[ {\left( {{n_x} - 11} \right)\lambda /2} \right]}^2} \bigg\} - \left[ {7\sqrt 3 \lambda + \left( {{n_x} - 11} \right)\lambda /2\tan ({\text{π }}/6)} \right]}}{{\dfrac{{\left( {{n_x} - 11} \right)\lambda }}{{\cos ({\text{π }}/6)}}}} $,
${\text{d}}{z_n} = \sqrt {{{\left( {7\sqrt 3 \lambda } \right)}^2} + {{\left[ {\left( {{n_x} - 11} \right)\lambda /2} \right]}^2} - {\text{d}}{x_n^2}} $.
下载: 导出CSV
-
[1] Qi Y H, Yang G, Liu L, Fan J, Antonio O, Kong H W, Yu W, Yang Z P 2017 IEEE Trans. Electromagn. Compat. 59 1661
Google Scholar
[2] 毕欣, 黄林, 杜劲松, 齐伟智, 高扬, 荣健, 蒋华北 2015 64 014301
Google Scholar
Bi X, Huang L, Du J S, Qi W Z, Gao Y, Rong J, Jiang H B 2015 Acta Phys. Sin. 64 014301
Google Scholar
[3] Seong H A, Chang H J, Dong M L, Wang S L 2020 IEEE Trans. Microwave Theory Tech. 68 2867
Google Scholar
[4] Yang Y, Fan Z P, Hong T, Chen M S, Tang X W, He J B, Chen X, Liu C J, Zhu H C, Huang K 2020 IEEE Trans. Microwave. Theory Tech. 68 4896
Google Scholar
[5] Giulio M B, Sara A, Gaetano M 2020 IEEE Trans. Antennas Propag. 68 6906
Google Scholar
[6] Wang J, Zheng Y N, He Z Y 2015 Antenna Array Theory and Engineering Applications (Vol. 1) (Beijing: Publishing House of Electronics Industry) pp93–101 (in Chines) [王建, 郑一农, 何子远 2015 阵列天线理论与工程应用 (北京: 电子工业出版社) 第93—101页
Wang J, Zheng Y N, He Z Y 2015 Antenna Array Theory and Engineering Applications (Vol. 1) (Beijing: Publishing House of Electronics Industry) pp93–101 (in Chines) [7] Li J Y, Qi Y X, Zhou S G 2017 IEEE Trans. Antennas Propag. 65 6157
Google Scholar
[8] Rao K S, Chakraborty A, Das B 1986 Antennas & Propagation Society International Symposium Philadelphia, PA, USA, June 08–13, 1986 p387
[9] Liu Y H, Liu Q H, Nie Z P 2010 IEEE Trans. Antennas Propag. 58 604
Google Scholar
[10] Shen H O, Wang B H, Li X 2017 IEEE Trans. Antennas Propag. 16 1098
Google Scholar
[11] Gu P F, Wang G, Fan Z H, Chen R S 2019 IEEE Trans. Antennas Propag. 67 7320
Google Scholar
[12] 张金玲, 万文钢, 郑占奇, 甘曦, 朱兴宇 2015 64 110504
Google Scholar
Zhang J L, Wen W G, Zheng Z Q, Gan X, Zhu X Y 2015 Acta Phys. Sin. 64 110504
Google Scholar
[13] Francisco J A P, Juan A R G, Emilio V L, S R R 1999 IEEE Trans. Antennas Propag. 47 506
Google Scholar
[14] Bitan M, G K Mahanti 2021 6th International Conference on Communication and Electronics Systems (ICCES) Coimbatre, India, July 8–10, 2021 p447
[15] Guo S, Zhao D S, Wang B Z 2022 IEEE Trans. Antennas Propag. 21 908
Google Scholar
[16] Elsa D T, Juan M C, Alejandro D M 2007 IEEE Trans. Microwave Theory Tech. 55 85
Google Scholar
[17] Kumari V, Ahmed A, Kanumuri T, Shakher C, Sheoran G 2020 Int. J. Imaging Syst. Technol. 30 391
Google Scholar
[18] 安腾远, 丁霄, 王秉中 2023 72 030401
Google Scholar
An T Y, Ding X, Wang B Z 2023 Acta Phys. Sin. 72 030401
Google Scholar
[19] Zhao D S, Zhu M 2016 IEEE Antennas Wireless Propag. Lett. 15 1739
Google Scholar
[20] 王秉中, 王任 2020 时间反演电磁学 (北京: 科学出版社 第165—179页
Wang B Z, Wang R 2020 Time Reversal Electromagnetism (Beijing: Science Press) pp165–179
[21] 臧锐, 王秉中, 丁帅, 龚志双 2016 65 204102
Google Scholar
Zang R, Wang B Z, Ding S, Gong Z S 2016 Acta Phys. Sin. 65 204102
Google Scholar
[22] 张知原, 李冰, 刘仕奇, 张洪林, 胡斌杰, 赵德双, 王楚楠 2022 71 014101
Google Scholar
Zhang Z Y, Li B, Liu S Q, Zhang H L, Hu B J, Zhao D S, Wang C N 2022 Acta Phys. Sin. 71 014101
Google Scholar
[23] Guo S, Zhao D S, Wang B Z, Cao W P 2020 IEEE Trans. Antennas Propag. 68 8249
Google Scholar
[24] Chen Z W, Liang F, Zhang Q L, Li B, Ge G D, Zhao D S 2021 IEEE Trans. Antennas Propag. 69 7011
Google Scholar
下载:
计量
- 文章访问数: 3834
- PDF下载量: 94
- 被引次数: 0
