相对论重离子碰撞中的手征效应实验研究

寿齐烨; 赵杰; 徐浩洁; 李威; 王钢; 唐爱洪; 王福强

doi:10.7498/aps.72.20230109

摘要

量子色动力学中夸克和拓扑胶子场的相互作用可以产生局域宇称和电荷共轭宇称不守恒, 这为解释宇宙中物质-反物质的不对称性提供了一种可能. 在强磁场下, 宇称不守恒会导致粒子按正负电荷分离, 此现象称为手征磁效应(CME). 相对论重离子对撞中与CME类似的手征反常效应还有手征涡旋效应(CVE), 以及手征磁波效应(CMW)等. 本文简要综述了当前相对论重离子碰撞实验中CME, CVE, CMW的研究进展.

关键词:

Abstract

In quantum chromodynamics, the interactions of quarks with the topological gluon field can lead to nonconservation of local parity (P) and conjugated parity (CP) , which provides a solution to the strong CP problem and a possibility to explain the asymmetry of matter-antimatter in the current universe. Under the action of a strong magnetic field, the nonconservation of P and CP can lead to the separation of particles according to their electric charges, which is called the chiral magnetic effect (CME). An observation of the CME-induced charge separation will confirm several fundamental properties of quantum chromodynamics (QCD), namely, approximate chiral symmetry restoration, topological charge fluctuation, and local parity violation. In relativistic heavy-ion collisions, there are other chiral anomalous effects similar to the CME, such as the chiral vortical effect (CVE) and the chiral magnetic wave (CMW). This review briefly summarizes the current progress of experimental research on the CME, CVE, and CMW in relativistic heavy-ion collisions.

Keywords:

作者及机构信息

1.
复旦大学现代物理研究所, 核物理与离子束应用教育部重点实验室, 上海　200433

2.
复旦大学, 国家自然科学基金委理论物理专款-上海核物理理论研究中心, 上海　200438

3.
湖州师范学院理学院, 湖州　313000

4.
莱斯大学物理与天文系, 休斯顿　77005, 美国

5.
加州大学洛杉矶分校物理与天文系, 洛杉矶　90095, 美国

6.
布鲁克海文国家实验室物理系, 纽约　11973, 美国

7.
普渡大学物理与天文系, 西拉法叶　47907, 美国

通信作者: 赵杰, jie_zhao@fudan.edu.cn ; 徐浩洁, haojiexu@zjhu.edu.cn ; 李威, wl33@rice.edu ; 王钢, gwang@physics.ucla.edu ; 唐爱洪, aihong@bnl.gov ; 王福强, fqwang@purdue.edu

基金项目: 国家自然科学基金(批准号: 12275053, 11975078, 12275082, 12035006, 12075085, 12147219)、上海市青年科技启明星(批准号: 20QA1401500)、国家重点研发计划(批准号: 2022YFA1604900)和美国能源部(批准号: DE-FG02-88ER40424, DE-AC02-98CH10886, DE-FG02-89ER40531, DE-SC0012910)资助的课题

Authors and contacts

1.
Key Laboratory of Nuclear Physics and Ion-beam Application, Ministry of Education, Institute of Modern Physics, Fudan University, Shanghai 200433, China

2.
Shanghai Research Center for Theoretical Nuclear Physics, National Natural Science Foundion of China, Fudan University, Shanghai 200438, China

3.
School of Science, Huzhou University, Huzhou 313000, China

4.
Department of Physics and Astronomy, Rice University, Houston 77005, USA

5.
Department of Physics and Astronomy, University of California, Los Angeles 90095, USA

6.
Department of Physics, Brookhaven National Laboratory, New York 11973, USA

7.
Department of Physics and Astronomy, Purdue University, West Lafayette IN 47907, USA

Corresponding author: Zhao Jie, jie_zhao@fudan.edu.cn ; Xu Hao-Jie, haojiexu@zjhu.edu.cn ; Li Wei, wl33@rice.edu ; Wang Gang, gwang@physics.ucla.edu ; Tang Ai-Hong, aihong@bnl.gov ; Wang Fu-Qiang, fqwang@purdue.edu

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 12275053, 11975078, 12275082, 12035006, 12075085, 12147219), the Shanghai Rising-Star Program, China (Grant No. 20QA1401500), the National Key R&D Program of China (Grant No. 2022YFA1604900), and the U.S. Department of Energy (Grant Nos. DE-FG02-88ER40424, DE-AC02-98CH10886, DE-FG02-89ER40531, DE-SC0012910)

文章全文 : translate this paragraph

参考文献

[1]	Belavin A A, Polyakov A M, Schwartz A S, Tyupkin Y S 1975 Phys. Lett. B 59 85 Google Scholar
[2]	Callan C G, Dashen R F, Gross D J 1976 Phys. Lett. B 63 334 Google Scholar
[3]	Hooft G T 1976 Phys. Rev. D 14 3432
[4]	Schäfer T, Shuryak E V 1998 Rev. Mod. Phys. 70 323 Google Scholar
[5]	Kharzeev D E, Levin E M. 2015 Phys. Rev. Lett. 114 242001 Google Scholar
[6]	Adler S L 1969 Phys. Rev. 177 2426 Google Scholar
[7]	Bell J S, Jackiw R 1969 Nuovo Cim. A 60 74
[8]	Kharzeev D E 2006 Phys. Lett. B 633 260 Google Scholar
[9]	Kharzeev D E, McLerran L D, Warringa H J 2008 Nucl. Phys. A2008 227
[10]	Li Q, Kharzeev D E, Zhang C, Huang Y, Pletikosic I, Fedorov A V, Zhong R D, Schneeloch J A, Gu G D, Valla T 2016 Nat. Phys. 12 550 Google Scholar
[11]	Xiong J, Kushwaha S K, Liang T, Krizan J W, Hirschberger M, Wang W, Cava R J, Ong N P 2015 Science 350 413 Google Scholar
[12]	Li C Z, Wang L X, Liu H W, Wang J, Liao Z M, Yu D P 2015 Nat. Commun. 6 10137 Google Scholar
[13]	Long Y J, Wang P P, Chen D, Yang Z H, Liang H, Xue M Q, Weng H M, Fang Z, Dai X, Chen G F, Huang X C, Zhao L X 2015 Phys. Rev. X 5 031023
[14]	Kharzeev D E, Liao J F, Voloshin S A, Wang G 2016 Prog. Part. Nucl. Phys. 88 1 Google Scholar
[15]	Zhao J 2018 Int. J. Mod. Phys. A 33 1830010 Google Scholar
[16]	Zhao J, Tu Z, Wang F Q 2018 Nucl. Phys. Rev. 35 225
[17]	Zhao J, Wang F Q 2019 Prog. Part. Nucl. Phys. 107 200 Google Scholar
[18]	Li W, Wang G 2020 Ann. Rev. Nucl. Part. Sci. 70 293 Google Scholar
[19]	Kharzeev D E, Liao J F 2021 Nat. Rev. Phys. 3 55
[20]	Abelev B I, Aggarwal M M, Ahammed Z, et al. 2009 Phys. Rev. Lett. 103 251601 Google Scholar
[21]	Abelev B I, Aggarwal M M, Ahammed Z, et al. 2010 Phys. Rev. C 81 054908 Google Scholar
[22]	Adamczyk L, Adkins J K, Agakishiev G, et al. 2014 Phys. Rev. Lett. 113 052302 Google Scholar
[23]	Abelev B I, Adam J , Adamova D, et al. 2013 Phys. Rev. Lett. 110 012301 Google Scholar
[24]	Voloshin S A 2004 Phys. Rev. C 70 057901 Google Scholar
[25]	Pratt S, Schlichting S, Gavin S 2011 Phys. Rev. C 84 024909 Google Scholar
[26]	Bzdak A, Koch V, Liao J F 2013 Lect. Notes Phys. 871 503
[27]	Schlichting S, Pratt S 2011 Phys. Rev. C 83 014913 Google Scholar
[28]	Lin Z W, Ko C M, Li B A, Zhang B, Pal S 2005 Phys. Rev. C 72 064901 Google Scholar
[29]	Lin Z W 2014 Phys. Rev. C 90 014904 Google Scholar
[30]	Lin Z W, Zheng L 2021 Nucl. Sci. Tech. 32 113 Google Scholar
[31]	Zhang H X, Xiao Y X, Kang J W, Zhang B W 2022 Nucl. Sci. Tech. 33 150 Google Scholar
[32]	Khachatryan V, et al. 2017 Phys. Rev. Lett. 118 122301 Google Scholar
[33]	Adam J, et al. 2019 Phys. Lett. B 798 134975 Google Scholar
[34]	Zhao J, Feng Y C, Li H L, Wang F Q 2020 Phys. Rev. C 101 034912 Google Scholar
[35]	Adamczyk L, et al. 2014 Phys. Rev. C 89 044908 Google Scholar
[36]	Tu B In Poster Given at 25th International Conference on Ultrarelativistic Nucleus-Nucleus Collisions (Quark Matter 2015) Kobe, Japan, September 27-October 3, 2015
[37]	Acharya S, et al. 2018 Phys. Lett. B 777 151 Google Scholar
[38]	Sirunyan A M, et al. 2018 Phys. Rev. C 97 044912 Google Scholar
[39]	Wang F Q, Zhao J 2017 Phys. Rev. C 95 051901 (R Google Scholar
[40]	Zhao J, Li H L, Wang F Q 2019 Eur. Phys. J. C 79 168 Google Scholar
[41]	Abdallah M S, et al. 2022 Phys. Rev. C 106 034908 Google Scholar
[42]	Xu H J, Zhao J, Wang X B, Li H L, Lin Z W, Shen C W, Wang F Q 2018 Chin. Phys. C 42 084103 Google Scholar
[43]	Abdallah M S, et al. 2022 Phys. Rev. Lett. 128 092301 Google Scholar
[44]	Abdallah M, et al. 2022 Phys. Rev. C 105 014901 Google Scholar
[45]	Voloshin S A 2010 Phys. Rev. Lett. 105 172301 Google Scholar
[46]	Deng W T, Huang X G, Ma G L, Wang G 2016 Phys. Rev. C 94 041901 Google Scholar
[47]	Koch V, Schlichting S, Skokov V, Sorensen P, Thomas J, Voloshin S, Wang G, Yee H U 2017 Chin. Phys. C 41 072001 Google Scholar
[48]	Adam J, et al. 2021 Nucl. Sci. Tech. 32 48 Google Scholar
[49]	Choudhury S, et al. 2022 Chin. Phys. C 46 014101 Google Scholar
[50]	Xu H J, Wang X B, Li H L, Zhao J, Lin Z W, Shen C W, Wang F Q 2018 Phys. Rev. Lett. 121 022301 Google Scholar
[51]	Li H L, Xu H J, Zhou Y, Wang X B, Zhao J, Chen L W, Wang F Q 2020 Phys. Rev. Lett. 125 222301 Google Scholar
[52]	Feng Y C 2023 EPJ Web Conf. 276 06013
[53]	Kharzeev D E, Liao J F, Shi S Z 2022 Phys. Rev. C 106 L051903 Google Scholar
[54]	Feng Y C, Lin Y F, Zhao J, Wang F Q 2021 Phys. Lett. B 820 136549 Google Scholar
[55]	Tang A H 2020 Chin. Phys. C 44 054101 Google Scholar
[56]	Shi S Z, Jiang Y, Lilleskov E, Liao J F 2018 Annals Phys. 394 50 Google Scholar
[57]	Jiang Y, Shi S Z, Yin Y, Liao J F 2018 Chin. Phys. C 42 011001 Google Scholar
[58]	Shi S Z, Zhang H, Hou D F, Liao J F 2020 Phys. Rev. Lett. 125 242301 Google Scholar
[59]	Ajitanand N N, Lacey R A, Taranenko A, Alexander J M 2011 Phys. Rev. C 83 011901 Google Scholar
[60]	Magdy N, Shi S Z, Liao J F, Ajitanand N N, Lacey R A 2018 Phys. Rev. C 97 061901 Google Scholar
[61]	Liu Y C, Huang X G 2020 Nucl. Sci. Tech. 31 56 Google Scholar
[62]	Gao J H, Ma G L, Pu S, Wang Q 2020 Nucl. Sci. Tech. 31 90 Google Scholar
[63]	赵新丽, 马国亮, 马余刚 2023 72 112502 Google Scholar Zhao X L, Ma G L, Ma Y G 2023 Acta Phys. Sin. 72 112502 Google Scholar
[64]	Kharzeev D E, Son D T 2011 Phys. Rev. Lett. 106 062301 Google Scholar
[65]	Jiang Y, Lin Z W, Liao J F 2016 Phys. Rev. C 94 044910 Google Scholar
[66]	Baznat M, Gudima M, Sorin A, Teryaev O 2016 Phys. Rev. C 93 031902 Google Scholar
[67]	Zhao F 2014 Nucl. Phys. A 931 746 Google Scholar
[68]	Zhao J 2017 EPJ Web Conf. 141 01010 Google Scholar
[69]	Wen L W 2017 Nucl. Phys. A 967 756 Google Scholar
[70]	Son D T, Zhitnitsky A R 2004 Phys. Rev. D 70 074018 Google Scholar
[71]	Metlitski M A, Zhitnitsky A R 2005 Phys. Rev. D 72 045011 Google Scholar
[72]	Burnier Y, Kharzeev D E, Liao J F, Yee H U 2011 Phys. Rev. Lett. 107 052303 Google Scholar
[73]	Adamczyk L, Adkins J K, Agakishiev G, et al. 2015 Phys. Rev. Lett. 114 252302 Google Scholar
[74]	Adam J, et al. 2016 Phys. Rev. C 93 044903 Google Scholar
[75]	Bzdak A, Boek P 2013 Phys. Lett. B 726 239
[76]	STAR Collaboration Search for the Chiral Magnetic Wave Using Anisotropic Flow of Identified Particles at RHIC arXiv: 2210.14027
[77]	Sirunyan A M, et al. 2019 Phys. Rev. C 100 064908 Google Scholar
[78]	Xu H J, Zhao J, Feng Y C, Wang F Q 2021 Nucl. Phys. A 1005 121770 Google Scholar
[79]	Ma G L 2014 Phys. Lett. B 735 383 Google Scholar
[80]	Voloshin S A, Belmont R 2014 Nucl. Phys. A 931 992 Google Scholar
[81]	Xu H J, Zhao J, Feng Y C, Wang F Q 2020 Phys. Rev. C 101 014913 Google Scholar
[82]	Wu W Y, Wang C Z, Shou Q Y, Ma Y G, Zheng L 2021 Phys. Rev. C 103 034906 Google Scholar
[83]	Wang C Z, Wu W Y, Shou Q Y, Ma G L, Ma Y G, Zhang S 2021 Phys. Lett. B 820 136580 Google Scholar
[84]	Wu W Y 2023 EPJ Web Conf. 276 01001
[85]	Hatta Y, Monnai A, Xiao B W 2016 Nucl. Phys. A 947 155 Google Scholar

施引文献

图 1 RHIC-STAR合作组于2009年左右对$ \gamma_{112} $关联函数的首次测量结果^[20,21]. 粗实线和虚线表示HIJING模型计算的三粒子关联背景贡献. 碰撞中心度从左到右增加; 0%对应于中心碰撞

Fig. 1. First measurement of the $ \gamma_{112} $ correlator from RHIC-STAR experiment around 2009^[20,21]. The thick solid (Au+Au) and dashed (Cu+Cu) lines represent HIJING calculations of the contributions from three-particle correlations. Collision centrality increases from left to right. 0% corresponds to the most central collisions

下载: 全尺寸图片幻灯片

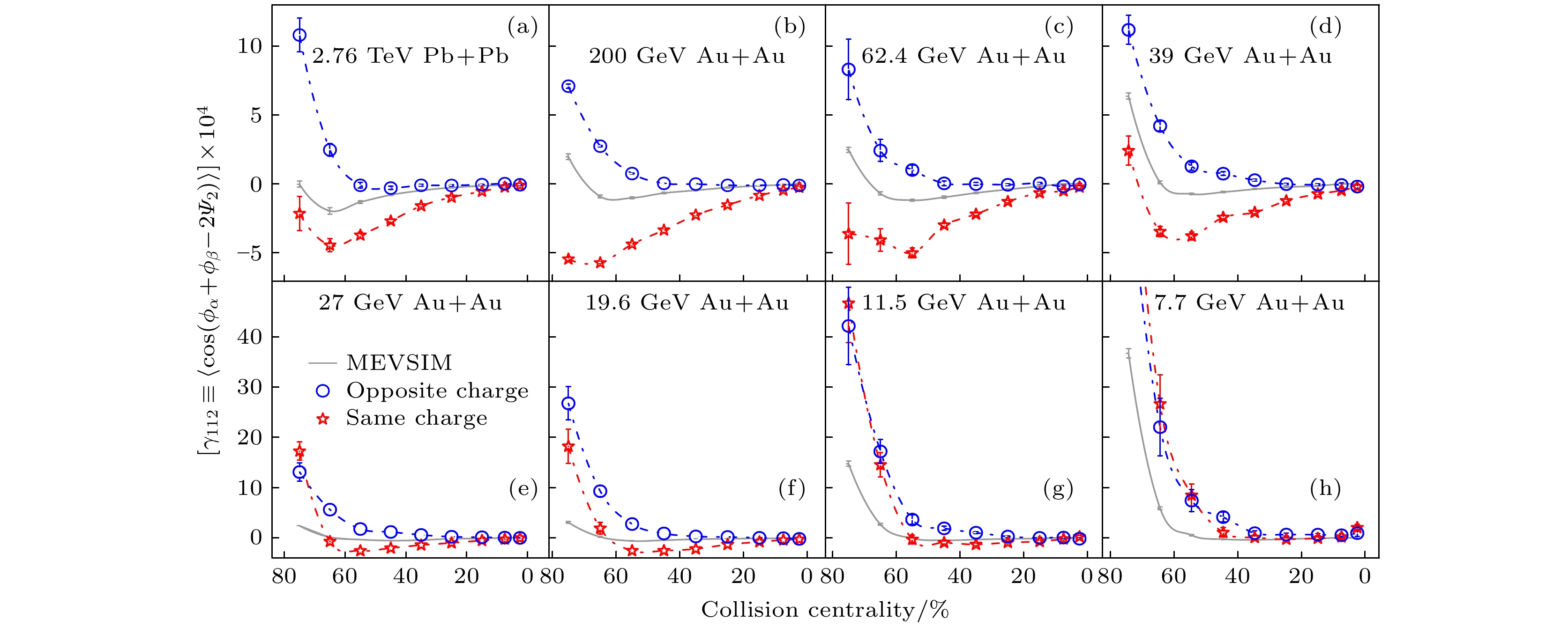
图 2 RHIC-STAR 7.7—200 GeV Au+Au以及LHC-ALICE 2.76 TeV Pb+Pb碰撞中$ \gamma_{112} $关联函数的中心度依赖性^[20-23]. 灰色线是MEVSIM模型估计的与电荷无关的背景贡献

Fig. 2. $ \gamma_{112} $ correlator as a function of centrality for Au+Au collisions at 7.7–200 GeV from RHIC-STAR, and for Pb+Pb collisions at 2.76 TeV from LHC-ALICE^[20-23]. Gray curves are the charge-independent results from MEVSIM calculations

下载: 全尺寸图片幻灯片

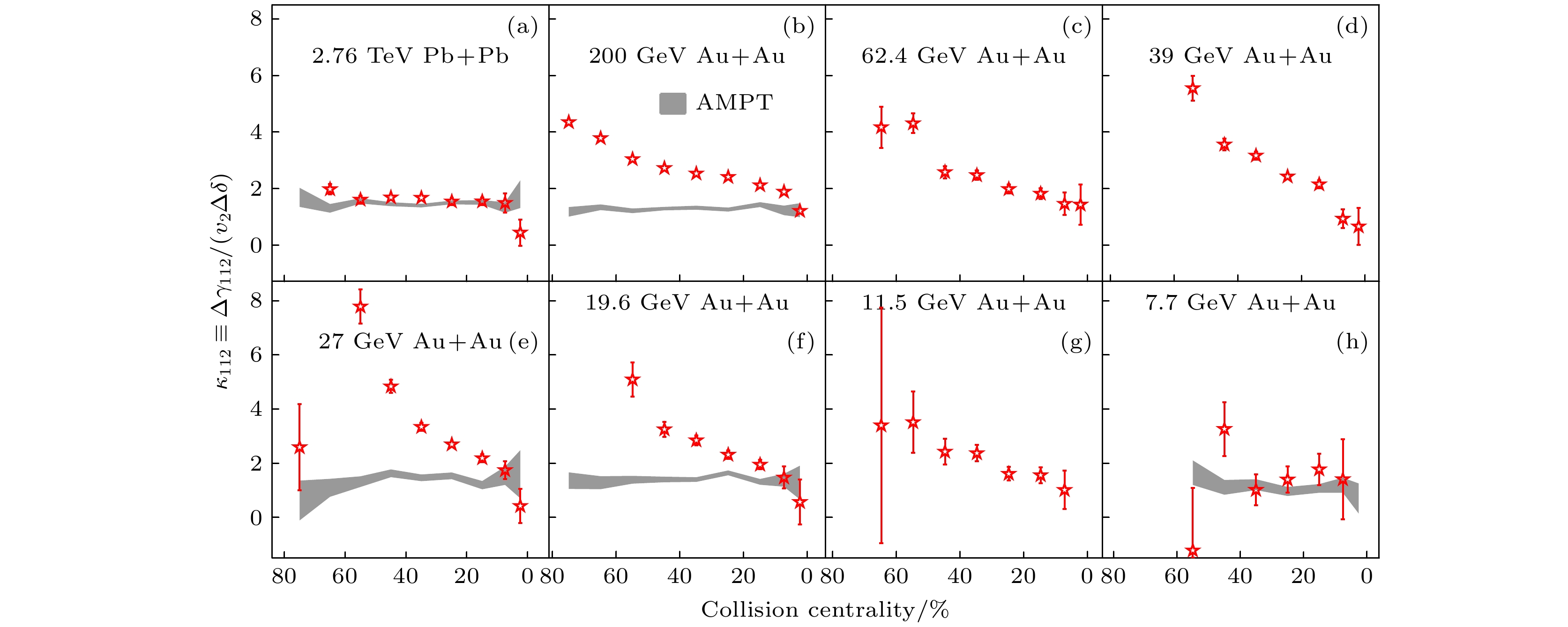
图 3 RHIC-STAR 7.7—200 GeV Au+Au以及LHC-ALICE 2.76 TeV Pb+Pb碰撞中$ \kappa_{112} $关联函数的中心度依赖性^[20-23]. 灰色粗实线是AMPT模型估计的与CME无关的背景贡献^[28-30]

Fig. 3. $ \kappa_{112} $ correlator as a function of centrality for Au+Au collisions at 7.7–200 GeV from RHIC-STAR, and for Pb+Pb collisions at 2.76 TeV from LHC-ALICE^[20-23]. Gray curves are the non-CME background estimations from AMPT^[28-30]

下载: 全尺寸图片幻灯片

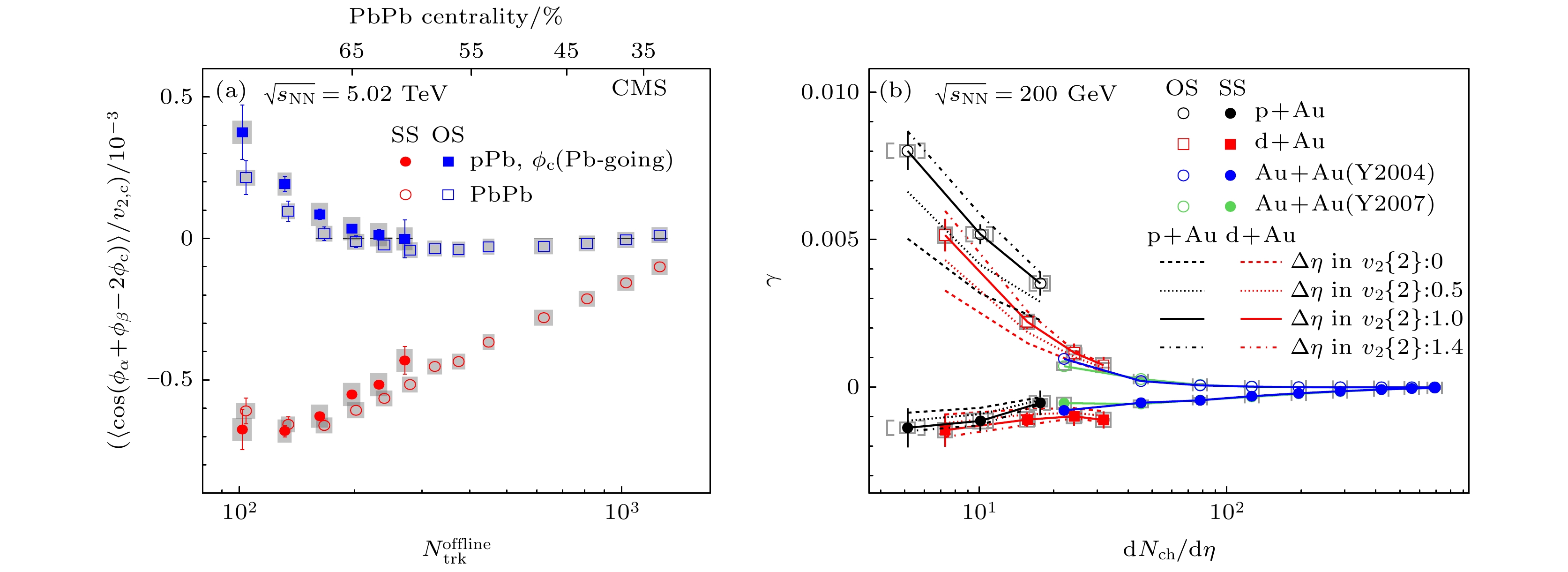
图 4 (a) LHC-CMS合作组在5.02 TeV p+Pb和 Pb+Pb碰撞中测量的$ \gamma_{112} $关联函数随多重数的依赖性^[32]; (b) RHIC-STAR合作组测量的小系统p+Au, d+Au碰撞中$ \gamma_{112} $关联函数与Au+Au碰撞结果的对比^[33]. 图中的灰色标记代表实验测量的系统误差

Fig. 4. (a) $ \gamma_{112} $ as a function of N in p+Pb and Pb+Pb collisions at 5.02 TeV from LHC-CMS collaboration^[32]; (b)$ \gamma_{112} $ as a function of N in p+Au, d+Au and Au+Au collisions at 200 GeV from RHIC-STAR collaboration^[33]. Systematic uncertainties are indicated by the shaded regions

下载: 全尺寸图片幻灯片

图 5 RHIC-STAR合作组通过事件形状筛选方法在200 GeV Au+Au碰撞中测量Δ关联函数与每个事件椭球形状观测量$ v_2^{\rm obs} $的关系^[35]

Fig. 5. Charge multiplicity asymmetry correlations (Δ) as a function of event-by-event $ v_2^{\rm obs} $ from 200 GeV Au+Au collisions^[35]

下载: 全尺寸图片幻灯片

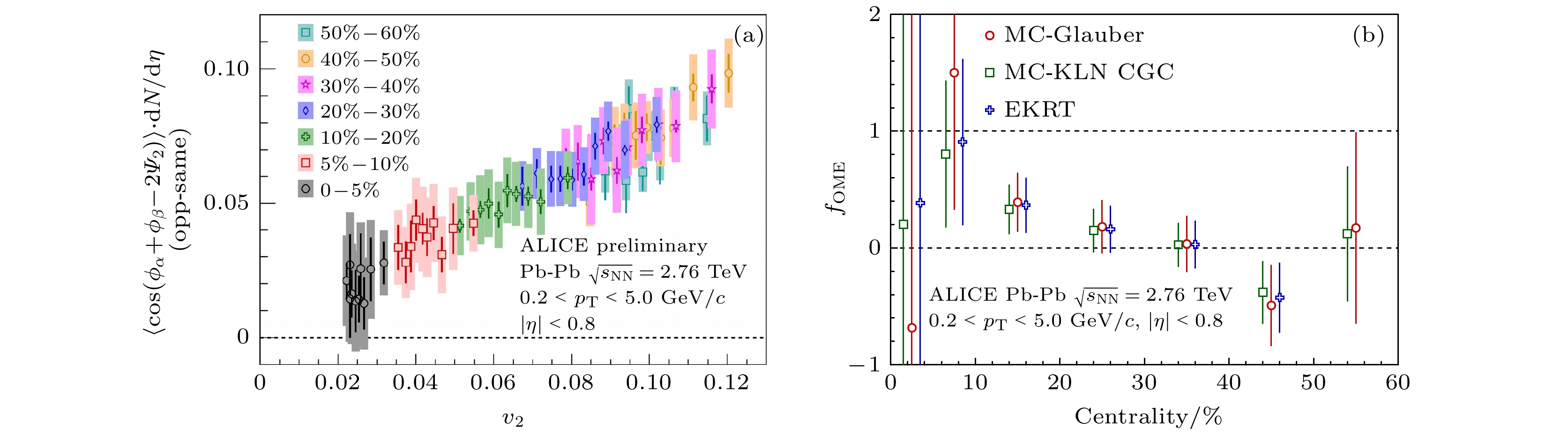
图 6 LHC-ALICE合作组(a)通过事件形状筛选方法在2.76 TeV Pb+Pb碰撞中测量的按粒子多重数缩放的$ \Delta\gamma_{112} $关联函数($\Delta\gamma_{112} \cdot {\rm{d}}N_{\rm ch}/{\rm{d}}\eta$)在不同中心度下随$ v_{2} $的关系, (b)通过事件形状筛选方法比较关联函数以及不同模型下磁场强度和$ v_{2} $的关系, 提取的手征磁效应的贡献^[37]

Fig. 6. (a) Charge-particle density scaled correlator ($\Delta\gamma_{112} \cdot {\rm{d}}N_{\rm ch}/{\rm{d}}\eta$) as a function of $ v_{2} $ for shape selected events in 2.76 TeV Pb+Pb collisions from LHC-ALICE; (b) extracted CME fraction ($ f_{\rm CME} $) by comparing the correlator and magnetic field dependence on $ v_{2} $ with different models^[37]

下载: 全尺寸图片幻灯片

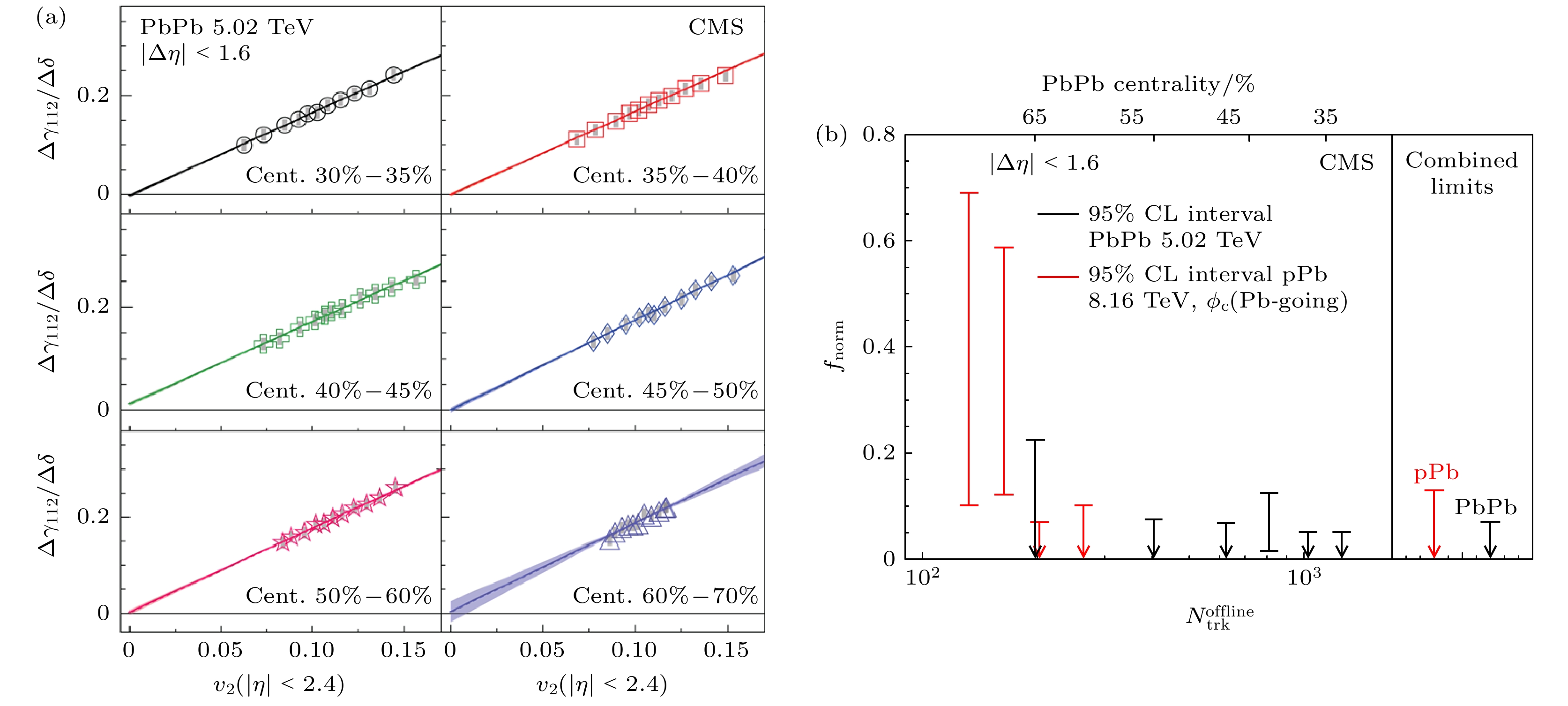
图 7 LHC-CMS合作组(a)通过事件形状筛选方法在5.02 TeV Pb+Pb碰撞中测量的按$ \Delta\delta $缩放的关联函数($ \Delta\gamma_{112}/\Delta\delta $)在不同中心度下随$ v_{2} $的关系, (b)通过事件形状筛选方法研究关联函数在$ v_{2}=0 $的结果, 提取的Pb+Pb以及p+Pb碰撞中手征磁效应的贡献^[38]

Fig. 7. (a) Scaled correlator, $ \Delta\gamma_{112}/\Delta\delta $, as a function of $ v_{2} $ evaluated with the ESE method, for different multiplicity ranges in Pb+Pb collisions from LHC-CMS; (b) extracted CME contributions, $ v_{2} $-independent component, in Pb+Pb and p+Pb collisions^[38]

下载: 全尺寸图片幻灯片

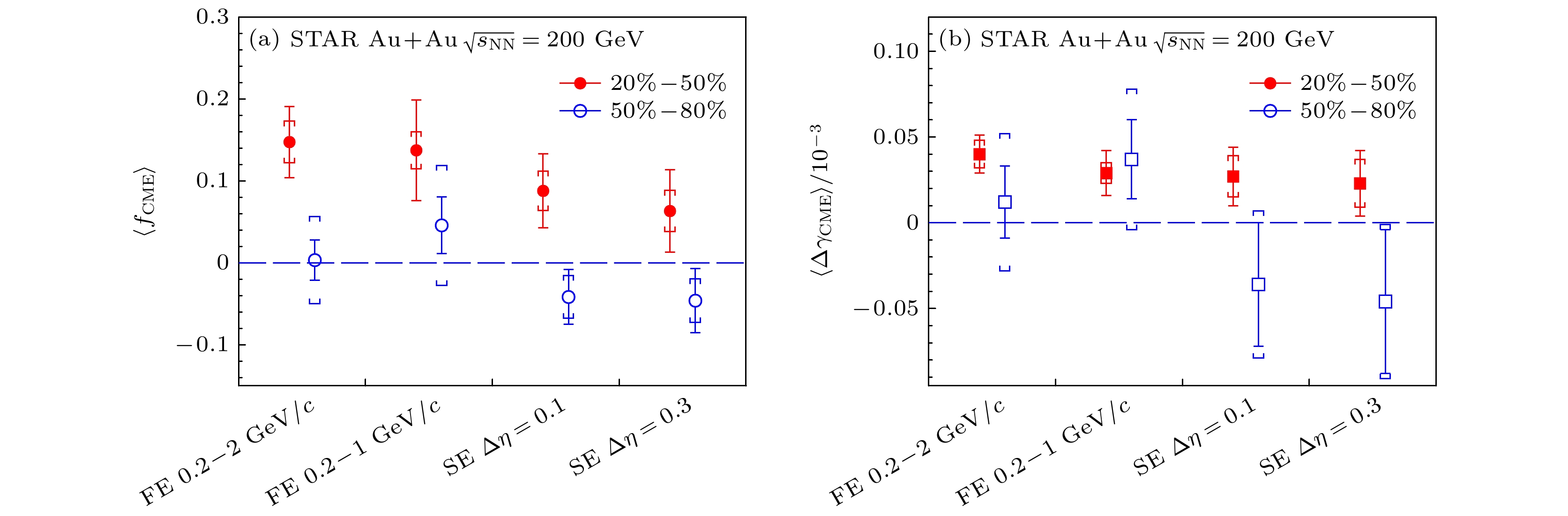
图 8 RHIC-STAR合作组(a)通过事件形状筛选方法选择的不同$ q_{2} $事件(A: large $ q_{2} $, B: small $ q_{2} $)中$ \Delta\gamma_{112} $关联函数与不变质量的关系, (b) A-B与无事件形状筛选的测量结果的比较^[41]

Fig. 8. (a) $ \Delta\gamma_{112} $ as functions of mass in different $ q_{2} $ events (A: large $ q_{2} $, B: small $ q_{2} $) using the event shape selection method; (b) inclusive measurement compared with the A-B^[41]

下载: 全尺寸图片幻灯片

图 9 RHIC-STAR合作组200 GeV Au+Au实验中通过比较旁观者平面和参与者平面测量结果而提取的手征磁效应信号百分比(a), 以及其信号大小(b)^[43]

Fig. 9. (a) Extracted CME fraction ($ f_{\rm CME} $) and (b) CME signal ($ \Delta\gamma_{\rm CME} $) using the spectator and participant planes method from RHIC-STAR^[43]

下载: 全尺寸图片幻灯片

图 10 RHIC-STAR合作组200 GeV 同位异素核Ru+Ru和Zr+Zr实验中的关联函数结果的比较^[44]

Fig. 10. Ratio of different observables between 200 GeV isobar Ru+Ru and Zr+Zr collisions from RHIC-STAR^[44]

下载: 全尺寸图片幻灯片

图 11 玩具模型显示$ r_{\mathrm{rest}} $和$R_{\rm{B}}$在不同CME强度下($ a_1 $)和共振态粒子椭圆流的关系^[55]

Fig. 11. $ r_{\mathrm{rest}} $ (Upper) and $ R_{\rm{B}} $ (Bottom) as functions of resonance $ v_{2} $ with different CME strength ($ a_1 $) using the Toy model simulation^[55]

下载: 全尺寸图片幻灯片

图 12 基于EBE-AVFD模拟数据计算的$ \Delta \gamma_{112} $ (a), $ \sigma^{-1}_{R2} $ ($ \sigma_{R2} $为R关联函数宽度) (c) 和 $ r_{\mathrm{lab}} $ (e) 关于$ n_{5}/s $的函数. $ n_{5}/s $在AVFD里表示原始植入的CME强度. 该计算是针对30%—40% 中心度同位异素$ \sqrt{s_{\rm NN}} = 200 $ GeV核核对撞. (b), (d), (f)观测量在Ru+Ru对Zr+Zr比值^[49]

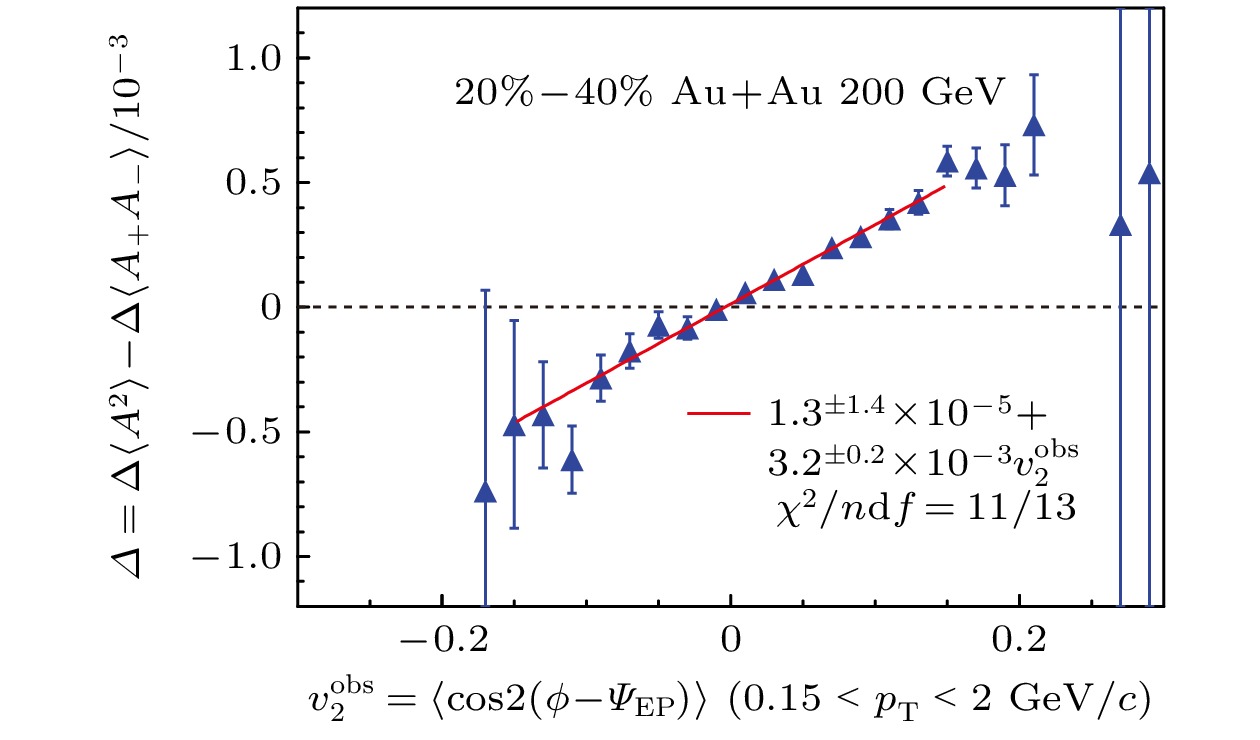
Fig. 12. $ \Delta \gamma_{112} $ (a), $ \sigma^{-1}_{R2} $ (c) and $ r_{\mathrm{lab}} $ (e) as functions of $ n_{5}/s $ in EBE-AVFD model simulation. (b), (d), (f) Corresponding ratios between Ru+Ru and Zr+Zr^[49]

下载: 全尺寸图片幻灯片

图 13 (a) STAR实验200 GeV Au+Au对撞中$ v_2^\pm $-$ A_{\rm ch} $的关系和(b)$ \Delta v_2 $-$ A_{\rm ch} $的关系^[73]; (c) ALICE实验2.76 TeV Pb+ Pb对撞中$ \Delta v_2 $-$ A_{\rm ch} $的关系 ^[74]

Fig. 13. (a)$ v_2^\pm $, (b) $ \Delta v_2 $ as functions of $ A_{\rm ch} $ in 200 GeV Au+Au collisions from STAR ^[73]; (c) $ \Delta v_2 $ as functions of $ A_{\rm ch} $ in 2.76 TeV Pb+Pb collisions from ALICE^[74]

下载: 全尺寸图片幻灯片

图 14 RHIC和LHC不同碰撞系统和能量下$ \Delta v_2 $-$ A_{\rm ch} $斜率的中心度依赖^[73,74]

Fig. 14. Slopes of the $ \Delta v_2 $-$ A_{\rm ch} $ as functions of centrality in different collisions systems and energies from RHIC and LHC^[73,74]

下载: 全尺寸图片幻灯片

图 15 (a) STAR实验200 GeVAu+Au对撞和(b) CMS实验5.02 TeV Pb+Pb对撞中观测到的$ r_2 $、$ r_3 $斜率, 在误差范围内基本一致^[76,77]

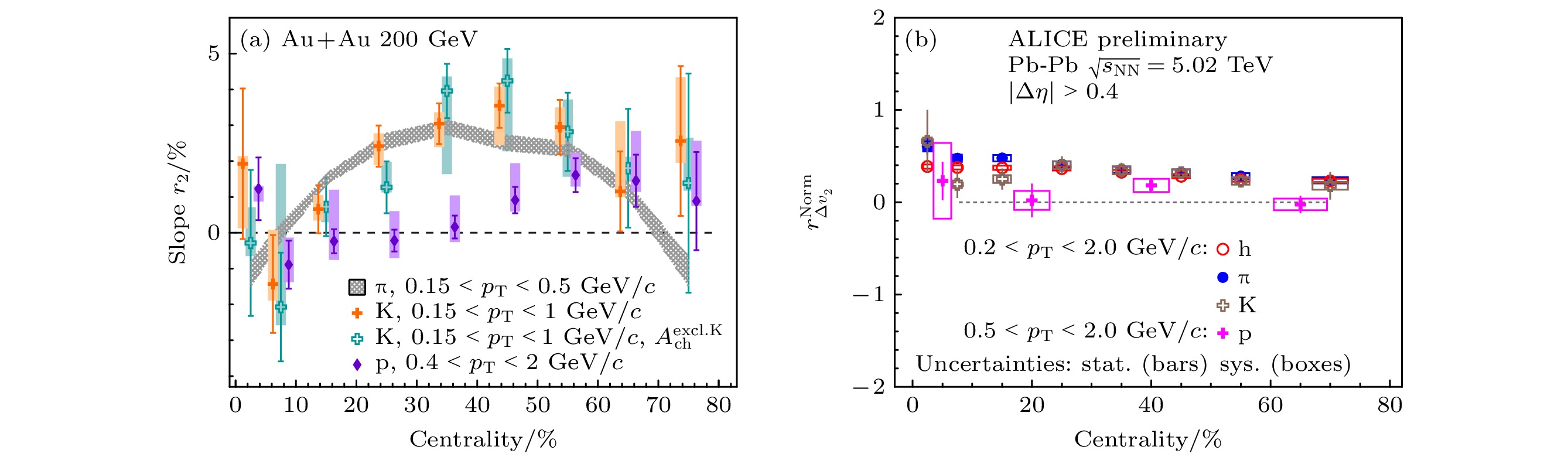
Fig. 15. Measured $ r_2 $, $ r_3 $ slopes as functions of centrality in 200 GeV Au+Au collisions from STAR (a), and in 5.02 TeV Pb+Pb collisions from CMS (b), within the uncertainties, the slopes of $ r_2 $, $ r_3 $ are consistent with each other^[76,77]

下载: 全尺寸图片幻灯片

图 16 (a) STAR实验200 GeVAu+Au、U+U、p+Au和d+Au对撞和(b) CMS实验5.02 TeV Pb+Pb和p+Pb对撞中观测到的$ r_2 $斜率^[76,77]

Fig. 16. Measured $ r_2 $ slopes as functions of multiplicity (a) in small system collisions of 200 GeV p+A, d+Au compared with Au+Au and U+U from STAR, and (b) in 5.02 TeV p+Pb and Pb+Pb collisions from CMS^[76,77]

下载: 全尺寸图片幻灯片

图 17 ALICE实验利用“事件形状筛选”方法得到(a)观测量和$ v_2 $显著的线性关联, 继而提取出(b) CMW信号在观测量中的占比^[84]

Fig. 17. Covariance of $ \Delta v_2 $ and $ A_{\rm ch} $ ($ \Delta \rm{Int.\; Cov.} $) as functions of $ v_2 $ from the ESE method (a) and (b) the corresponding extracted CMW fraction^[84]

下载: 全尺寸图片幻灯片

图 18 (a) STAR实验200 GeVAu+Au对撞和(b) ALICE实验5.02 TeV Pb+Pb对撞中可鉴别强子π, K, p的$ r_2 $斜率, π和K的结果在误差范围内基本一致^[76,84]

Fig. 18. Measured $ r_2 $ slopes of identified particles (π, K, p) as functions of centrality in (a) 200 GeV Au+Au collisions from STAR, and (b) in 5.02 TeV Pb+Pb collisions from ALICE^[76,84]

下载: 全尺寸图片幻灯片

map

[1]	Belavin A A, Polyakov A M, Schwartz A S, Tyupkin Y S 1975 Phys. Lett. B 59 85 Google Scholar
[2]	Callan C G, Dashen R F, Gross D J 1976 Phys. Lett. B 63 334 Google Scholar
[3]	Hooft G T 1976 Phys. Rev. D 14 3432
[4]	Schäfer T, Shuryak E V 1998 Rev. Mod. Phys. 70 323 Google Scholar
[5]	Kharzeev D E, Levin E M. 2015 Phys. Rev. Lett. 114 242001 Google Scholar
[6]	Adler S L 1969 Phys. Rev. 177 2426 Google Scholar
[7]	Bell J S, Jackiw R 1969 Nuovo Cim. A 60 74
[8]	Kharzeev D E 2006 Phys. Lett. B 633 260 Google Scholar
[9]	Kharzeev D E, McLerran L D, Warringa H J 2008 Nucl. Phys. A2008 227
[10]	Li Q, Kharzeev D E, Zhang C, Huang Y, Pletikosic I, Fedorov A V, Zhong R D, Schneeloch J A, Gu G D, Valla T 2016 Nat. Phys. 12 550 Google Scholar
[11]	Xiong J, Kushwaha S K, Liang T, Krizan J W, Hirschberger M, Wang W, Cava R J, Ong N P 2015 Science 350 413 Google Scholar
[12]	Li C Z, Wang L X, Liu H W, Wang J, Liao Z M, Yu D P 2015 Nat. Commun. 6 10137 Google Scholar
[13]	Long Y J, Wang P P, Chen D, Yang Z H, Liang H, Xue M Q, Weng H M, Fang Z, Dai X, Chen G F, Huang X C, Zhao L X 2015 Phys. Rev. X 5 031023
[14]	Kharzeev D E, Liao J F, Voloshin S A, Wang G 2016 Prog. Part. Nucl. Phys. 88 1 Google Scholar
[15]	Zhao J 2018 Int. J. Mod. Phys. A 33 1830010 Google Scholar
[16]	Zhao J, Tu Z, Wang F Q 2018 Nucl. Phys. Rev. 35 225
[17]	Zhao J, Wang F Q 2019 Prog. Part. Nucl. Phys. 107 200 Google Scholar
[18]	Li W, Wang G 2020 Ann. Rev. Nucl. Part. Sci. 70 293 Google Scholar
[19]	Kharzeev D E, Liao J F 2021 Nat. Rev. Phys. 3 55
[20]	Abelev B I, Aggarwal M M, Ahammed Z, et al. 2009 Phys. Rev. Lett. 103 251601 Google Scholar
[21]	Abelev B I, Aggarwal M M, Ahammed Z, et al. 2010 Phys. Rev. C 81 054908 Google Scholar
[22]	Adamczyk L, Adkins J K, Agakishiev G, et al. 2014 Phys. Rev. Lett. 113 052302 Google Scholar
[23]	Abelev B I, Adam J , Adamova D, et al. 2013 Phys. Rev. Lett. 110 012301 Google Scholar
[24]	Voloshin S A 2004 Phys. Rev. C 70 057901 Google Scholar
[25]	Pratt S, Schlichting S, Gavin S 2011 Phys. Rev. C 84 024909 Google Scholar
[26]	Bzdak A, Koch V, Liao J F 2013 Lect. Notes Phys. 871 503
[27]	Schlichting S, Pratt S 2011 Phys. Rev. C 83 014913 Google Scholar
[28]	Lin Z W, Ko C M, Li B A, Zhang B, Pal S 2005 Phys. Rev. C 72 064901 Google Scholar
[29]	Lin Z W 2014 Phys. Rev. C 90 014904 Google Scholar
[30]	Lin Z W, Zheng L 2021 Nucl. Sci. Tech. 32 113 Google Scholar
[31]	Zhang H X, Xiao Y X, Kang J W, Zhang B W 2022 Nucl. Sci. Tech. 33 150 Google Scholar
[32]	Khachatryan V, et al. 2017 Phys. Rev. Lett. 118 122301 Google Scholar
[33]	Adam J, et al. 2019 Phys. Lett. B 798 134975 Google Scholar
[34]	Zhao J, Feng Y C, Li H L, Wang F Q 2020 Phys. Rev. C 101 034912 Google Scholar
[35]	Adamczyk L, et al. 2014 Phys. Rev. C 89 044908 Google Scholar
[36]	Tu B In Poster Given at 25th International Conference on Ultrarelativistic Nucleus-Nucleus Collisions (Quark Matter 2015) Kobe, Japan, September 27-October 3, 2015
[37]	Acharya S, et al. 2018 Phys. Lett. B 777 151 Google Scholar
[38]	Sirunyan A M, et al. 2018 Phys. Rev. C 97 044912 Google Scholar
[39]	Wang F Q, Zhao J 2017 Phys. Rev. C 95 051901 (R Google Scholar
[40]	Zhao J, Li H L, Wang F Q 2019 Eur. Phys. J. C 79 168 Google Scholar
[41]	Abdallah M S, et al. 2022 Phys. Rev. C 106 034908 Google Scholar
[42]	Xu H J, Zhao J, Wang X B, Li H L, Lin Z W, Shen C W, Wang F Q 2018 Chin. Phys. C 42 084103 Google Scholar
[43]	Abdallah M S, et al. 2022 Phys. Rev. Lett. 128 092301 Google Scholar
[44]	Abdallah M, et al. 2022 Phys. Rev. C 105 014901 Google Scholar
[45]	Voloshin S A 2010 Phys. Rev. Lett. 105 172301 Google Scholar
[46]	Deng W T, Huang X G, Ma G L, Wang G 2016 Phys. Rev. C 94 041901 Google Scholar
[47]	Koch V, Schlichting S, Skokov V, Sorensen P, Thomas J, Voloshin S, Wang G, Yee H U 2017 Chin. Phys. C 41 072001 Google Scholar
[48]	Adam J, et al. 2021 Nucl. Sci. Tech. 32 48 Google Scholar
[49]	Choudhury S, et al. 2022 Chin. Phys. C 46 014101 Google Scholar
[50]	Xu H J, Wang X B, Li H L, Zhao J, Lin Z W, Shen C W, Wang F Q 2018 Phys. Rev. Lett. 121 022301 Google Scholar
[51]	Li H L, Xu H J, Zhou Y, Wang X B, Zhao J, Chen L W, Wang F Q 2020 Phys. Rev. Lett. 125 222301 Google Scholar
[52]	Feng Y C 2023 EPJ Web Conf. 276 06013
[53]	Kharzeev D E, Liao J F, Shi S Z 2022 Phys. Rev. C 106 L051903 Google Scholar
[54]	Feng Y C, Lin Y F, Zhao J, Wang F Q 2021 Phys. Lett. B 820 136549 Google Scholar
[55]	Tang A H 2020 Chin. Phys. C 44 054101 Google Scholar
[56]	Shi S Z, Jiang Y, Lilleskov E, Liao J F 2018 Annals Phys. 394 50 Google Scholar
[57]	Jiang Y, Shi S Z, Yin Y, Liao J F 2018 Chin. Phys. C 42 011001 Google Scholar
[58]	Shi S Z, Zhang H, Hou D F, Liao J F 2020 Phys. Rev. Lett. 125 242301 Google Scholar
[59]	Ajitanand N N, Lacey R A, Taranenko A, Alexander J M 2011 Phys. Rev. C 83 011901 Google Scholar
[60]	Magdy N, Shi S Z, Liao J F, Ajitanand N N, Lacey R A 2018 Phys. Rev. C 97 061901 Google Scholar
[61]	Liu Y C, Huang X G 2020 Nucl. Sci. Tech. 31 56 Google Scholar
[62]	Gao J H, Ma G L, Pu S, Wang Q 2020 Nucl. Sci. Tech. 31 90 Google Scholar
[63]	赵新丽, 马国亮, 马余刚 2023 72 112502 Google Scholar Zhao X L, Ma G L, Ma Y G 2023 Acta Phys. Sin. 72 112502 Google Scholar
[64]	Kharzeev D E, Son D T 2011 Phys. Rev. Lett. 106 062301 Google Scholar
[65]	Jiang Y, Lin Z W, Liao J F 2016 Phys. Rev. C 94 044910 Google Scholar
[66]	Baznat M, Gudima M, Sorin A, Teryaev O 2016 Phys. Rev. C 93 031902 Google Scholar
[67]	Zhao F 2014 Nucl. Phys. A 931 746 Google Scholar
[68]	Zhao J 2017 EPJ Web Conf. 141 01010 Google Scholar
[69]	Wen L W 2017 Nucl. Phys. A 967 756 Google Scholar
[70]	Son D T, Zhitnitsky A R 2004 Phys. Rev. D 70 074018 Google Scholar
[71]	Metlitski M A, Zhitnitsky A R 2005 Phys. Rev. D 72 045011 Google Scholar
[72]	Burnier Y, Kharzeev D E, Liao J F, Yee H U 2011 Phys. Rev. Lett. 107 052303 Google Scholar
[73]	Adamczyk L, Adkins J K, Agakishiev G, et al. 2015 Phys. Rev. Lett. 114 252302 Google Scholar
[74]	Adam J, et al. 2016 Phys. Rev. C 93 044903 Google Scholar
[75]	Bzdak A, Boek P 2013 Phys. Lett. B 726 239
[76]	STAR Collaboration Search for the Chiral Magnetic Wave Using Anisotropic Flow of Identified Particles at RHIC arXiv: 2210.14027
[77]	Sirunyan A M, et al. 2019 Phys. Rev. C 100 064908 Google Scholar
[78]	Xu H J, Zhao J, Feng Y C, Wang F Q 2021 Nucl. Phys. A 1005 121770 Google Scholar
[79]	Ma G L 2014 Phys. Lett. B 735 383 Google Scholar
[80]	Voloshin S A, Belmont R 2014 Nucl. Phys. A 931 992 Google Scholar
[81]	Xu H J, Zhao J, Feng Y C, Wang F Q 2020 Phys. Rev. C 101 014913 Google Scholar
[82]	Wu W Y, Wang C Z, Shou Q Y, Ma Y G, Zheng L 2021 Phys. Rev. C 103 034906 Google Scholar
[83]	Wang C Z, Wu W Y, Shou Q Y, Ma G L, Ma Y G, Zhang S 2021 Phys. Lett. B 820 136580 Google Scholar
[84]	Wu W Y 2023 EPJ Web Conf. 276 01001
[85]	Hatta Y, Monnai A, Xiao B W 2016 Nucl. Phys. A 947 155 Google Scholar

[1]	曾超, 毛一屹, 吴骥宙, 苑涛, 戴汉宁, 陈宇翱. 一维超冷原子动量光晶格中的手征对称性破缺拓扑相. , 2024, 73(4): 040301. doi: 10.7498/aps.73.20231566
[2]	. 高能重离子碰撞过程的自旋与手征效应专题编者按. , 2023, 72(7): 070101. doi: 10.7498/aps.72.070101
[3]	赵新丽, 马国亮, 马余刚. 中高能重离子碰撞中的电磁场效应和手征反常现象. , 2023, 72(11): 112502. doi: 10.7498/aps.72.20230245
[4]	白靖, 葛城显, 何浪, 刘轩, 吴振森. 椭圆波束对非均匀手征分层粒子的俘获特性研究. , 2022, 71(10): 104208. doi: 10.7498/aps.71.20212284
[5]	周淑英, 沈婉萍, 毛鸿. 强子夸克相变表面张力解析求解. , 2022, 71(21): 211101. doi: 10.7498/aps.71.20220659
[6]	王靖. 手征马约拉纳费米子. , 2020, 69(11): 117302. doi: 10.7498/aps.69.20200534
[7]	滕利华, 牟丽君. 掺杂对称性对(110)晶向生长GaAs/AlGaAs量子阱中电子自旋弛豫动力学的影响}. , 2017, 66(4): 046802. doi: 10.7498/aps.66.046802
[8]	李明林, 万亚玲, 胡建玥, 王卫东. 单层二硫化钼力学性能温度和手性效应的分子动力学模拟. , 2016, 65(17): 176201. doi: 10.7498/aps.65.176201
[9]	肖文德, 刘立巍, 杨锴, 张礼智, 宋博群, 杜世萱, 高鸿钧. 氢原子吸附对金表面金属酞菁分子的吸附位置、自旋和手征性的调控. , 2015, 64(7): 076802. doi: 10.7498/aps.64.076802
[10]	张毅. 相对论性力学系统的Birkhoff对称性与守恒量. , 2012, 61(21): 214501. doi: 10.7498/aps.61.214501
[11]	贾利群, 解银丽, 罗绍凯. 相对运动动力学系统Appell方程Mei对称性导致的Mei守恒量. , 2011, 60(4): 040201. doi: 10.7498/aps.60.040201
[12]	解银丽, 贾利群, 杨新芳. 相对运动动力学系统Nielsen方程的Lie对称性与Hojman守恒量. , 2011, 60(3): 030201. doi: 10.7498/aps.60.030201
[13]	徐进, 王文祥, 岳玲娜, 宫玉彬, 魏彦玉. 椭圆手征波导的传输特性. , 2009, 58(9): 6291-6295. doi: 10.7498/aps.58.6291
[14]	梅凤翔, 吴惠彬. 相对运动动力学系统的Lagrange对称性. , 2009, 58(9): 5919-5922. doi: 10.7498/aps.58.5919
[15]	张毅, 葛伟宽. 相对论性力学系统的Mei对称性导致的新守恒律. , 2005, 54(4): 1464-1467. doi: 10.7498/aps.54.1464
[16]	方建会, 陈培胜, 张军, 李红. 相对论力学系统的形式不变性与Lie对称性. , 2003, 52(12): 2945-2948. doi: 10.7498/aps.52.2945
[17]	方建会, 闫向宏, 陈培胜. 相对论力学系统的形式不变性与Noether对称性. , 2003, 52(7): 1561-1564. doi: 10.7498/aps.52.1561
[18]	阮建红, 薛迅, 朱伟. 量子色动力学演化方程中的高扭度效应. , 2002, 51(6): 1214-1220. doi: 10.7498/aps.51.1214
[19]	罗绍凯, 傅景礼, 陈向炜. 转动系统相对论性Birkhoff动力学的基本理论. , 2001, 50(3): 383-389. doi: 10.7498/aps.50.383
[20]	贾春生, 蒋效卫, 王孝国, 杨秋波. 量子系统的能量本征值在超对称性、形状不变性框架下的计算. , 1997, 46(1): 12-19. doi: 10.7498/aps.46.12

计量

文章访问数: 4394
PDF下载量: 94
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

相对论重离子碰撞中的手征效应实验研究