-
水下涡流场对声波的散射问题是声波在复杂流场中传播的基本问题, 在水下目标探测和流场声成像领域具有重要意义. 针对水下低频振荡涡流场声散射调制问题建立了理论分析模型与数值计算方法, 探究了其声散射调制声场的产生机理与时空频特性. 首先, 基于运动介质的波动方程, 通过引入势函数将波动方程分解为流声耦合项和非耦合项, 并对流声耦合项进行频域分析处理, 揭示了水下振荡涡流场的声散射调制机理; 其次, 采用间断伽辽金数值方法对水下低频振荡涡流场中声传播过程进行了数值模拟, 分析了低马赫数条件下, 不同入射声波频率、涡流场的振荡频率和涡核尺度对涡流场声散射调制声场时空频特性的影响规律, 并结合理论分析模型对其特性进行了解释. 研究表明: 低马赫数下, 振荡涡流场对声波的散射可产生包含涡流场振荡频率双边带调制谐波的散射调制声场, 且随着入射声波频率、涡核尺度的增大, 散射调制声场强度增强, 总散射声场空间分布具有对称性和明显主瓣, 且主瓣方位角趋近于入射波传播方向; 在频率比远大于1条件下, 涡流场振荡频率对散射调制声场强度影响较小.The scattering of sound waves by underwater vortex flow filed is the basic problem of sound waves propagating in complex flow fields, which has important significance in implementing underwater target detection and sound imaging of flow field. The theoretical analysis model and numerical calculation method are established for the problem of sound scattering modulation in underwater low frequency oscillating vortex flow fields, and the generation mechanism and time frequency and space characteristics of the scattering modulation sound field are explored. Firstly, based on the wave equation of the moving medium, in the first-order approximation the wave equation is decomposed into the flow-sound coupling term and the non flow-sound coupling term by introducing a potential function, and the flow-sound coupling term is analyzed in the frequency domain, revealing the underwater oscillating vortex flow field. Secondly, the discontinuous Galerkin numerical calculation method is used to solve the wave equation of the moving medium, and the sound propagation process in the underwater low frequency oscillating vortex flow field is numerically simulated. Under the condition of low Mach number, the effects of incident sound frequency, the oscillation frequency of the vortex flow field, and the scale of the vortex core on the time-frequency and space characteristics of the scattering modulating sound fields of vortex flow field are analyzed, and theoretical analysis model is used to explain the characteristics. The research results show that under the condition of low Mach number, the scattering of sound wave by oscillating vortex flow field can produce a scattering modulated sound field containing the harmonic of oscillating frequency side frequency modulation. The amplitude of the scattered sound pressure changes periodically with time, and the forward scattering is much stronger than the backward scattering. The fundamental frequency scattering modulation is much stronger than the frequency doubling scattering modulation. With the increase of the frequency of the incident sound wave and the scale of the vortex core, the intensity of the scattering modulating sound field increases, and the spatial distribution of the total scattering sound field has symmetry and an obvious main lobe, the main lobe is gradually sharpened, the azimuth angle of the main lobe is close to the propagation direction of the incident wave. When the frequency ratio is much greater than 1, the vortex flow field oscillation frequency has little effect on the spatial distribution of the sound field intensity of scattering modulating sound field.
[1] Ostashev V E, Wilson D K 2015 Acoustics in Moving Inhomogeneous Media (New York: CRC Press) pp1–23
[2] Aurégan Y, Maurel A, Pagneux V 2008 Sound-Flow Interactions (Berlin: Springer) pp112–158
[3] Chakraborty P, Balachandar S, Adrian R J 2005 J. Fluid Mech. 535 189
Google Scholar
[4] Clair V, Gabard G 2018 J. Fluid Mech. 841 50
Google Scholar
[5] Colonius T, Lele S K, Moin P 1994 J. Fluid Mech. 260 271
Google Scholar
[6] Karabasov S, Kopiev V, Goloviznin V 2009 Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference) Miami, USA, May 10–12, 2009
[7] 马瑞轩, 王益民, 张树海, 武从海, 王勋年 2021 70 104301
Google Scholar
Ma R X, Wang Y M, Zhang S H, Wu C H, Wang X N 2021 Acta Phys. Sin. 70 104301
Google Scholar
[8] 王益民, 马瑞轩, 武从海, 罗勇, 张树海 2021 79 194302
Google Scholar
Wang Y M, Ma R X, Wu C H, Luo Y, Zhang S H 2021 Acta Phys. Sin. 79 194302
Google Scholar
[9] Semenov A G. 2017 Ultra Low Frequency Fields of Moving Bodies (New York: Nova Science Publishers) pp118–141
[10] Catalano P, Wang M, Iaccarino G 2003 Int. J. Heat Fluid Fl. 24 463
Google Scholar
[11] Zdravkovich M M 1997 Flow Around Circular Cylinders: Volume 2: Applications (Oxford: Oxford University Press) pp163–201
[12] Lighthill M J 1953 Proc. Cambridge Philos. Soc. 49 531
Google Scholar
[13] Kraichnan R H 1953 J. Acoust. Soc. Am. 25 1096
Google Scholar
[14] Bogey C, Bailly C, Juve D 2002 AIAA J. 40 235
Google Scholar
[15] Bailly C, Juve D 2000 AIAA J. 38 22
Google Scholar
[16] Pierce A D. 2019 Acoustics: An Introduction to Its Physical Principles and Applications (East Sandwich: Springer) pp427– 480
[17] Pierce A D 1990 J. Acoust. Soc. Am. 87 2292
Google Scholar
[18] Cheinet S, Ehrhardt L, Juve D, Benon B P 2012 J. Acoust. Soc. Am. 132 2198
Google Scholar
[19] Cockburn B, Shu C W 2001 J. Sci. Comput. 16 173
Google Scholar
[20] Cockburn B, Shu C W 1989 Math. Comp. 52 411
Google Scholar
[21] Lee H D, Kwon O J 2013 J. Mech. Sci. Technol. 27 3331
Google Scholar
[22] Williamschen M, Gabard G J 2020 AIAA J. 58 1079
Google Scholar
[23] 程建春 2019 声学原理(第二版下卷) (北京: 科学出版社) 第969页
Cheng J C 2012 Acoustic principles (Volume II of the Second Edition) (Beijing: Science Press) p969 (in Chinese)
[24] 冯士筰, 李凤岐, 李少菁 1999 海洋科学导论 (北京: 高等教育出版社) 第181页
Feng S Z, Li F Q, Li S J 1999 Introduction to Marine Science (Beijing: Higher Education Press) p181 (in Chinese)
[25] 杜浩, 熊鳌魁, 张咏鸥 2020 声学学报 45 55
Google Scholar
Du H, Xiong A K, Zhang Y O 2020 Acta Acoust. 45 55
Google Scholar
[26] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics (New York: Springer) pp531– 610
[27] Headrick R H, Lynch J F, Kemp J N, Newhall A E, Heydt K 2000 J. Acoust. Soc. Am. 107 201
Google Scholar
[28] Ford R, Smith S G L 1999 J. Fluid Mech. 386 305
Google Scholar
[29] Fetter A L 1964 Phys. Rev. A 136 1488
Google Scholar
-
图 2 不同时刻
$ x = 0 $ 轴线涡流场速度分布Fig. 2. Velocity distribution of vortex flow field on
$ x = 0 $ axis at different time.
图 4 网格无关性和时间步长无关性验证 (a) 网格无关性验证; (b)时间步长无关性验证
Fig. 4. Verification of grid independence and time step independence: (a) Grid independence verification; (b) time step independence verification.
图 5 定常涡流场与振荡涡流场散射指向性图
Fig. 5. Scattering directivity of steady vortex flow field and oscillating vortex flow field.
图 7
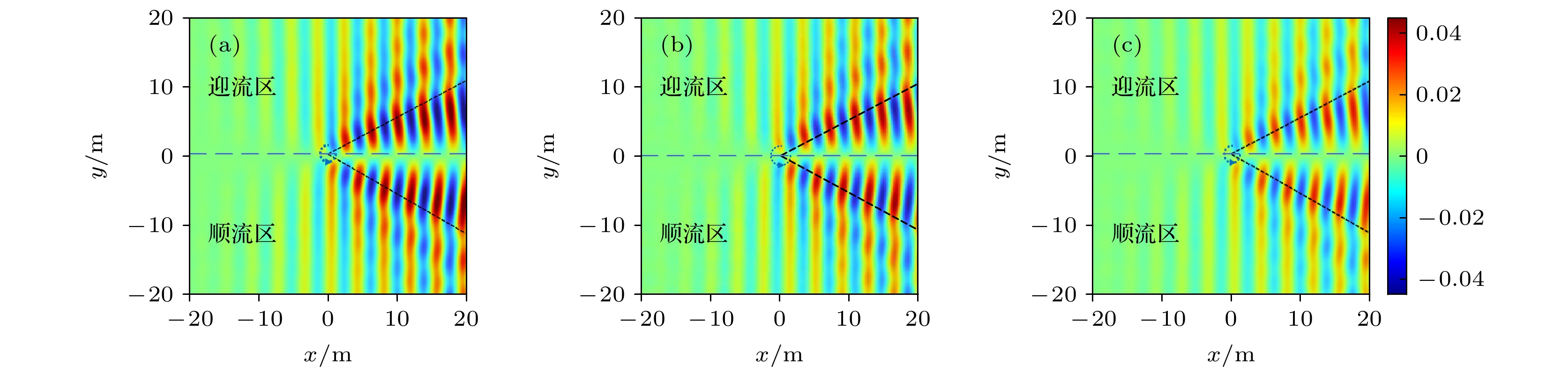
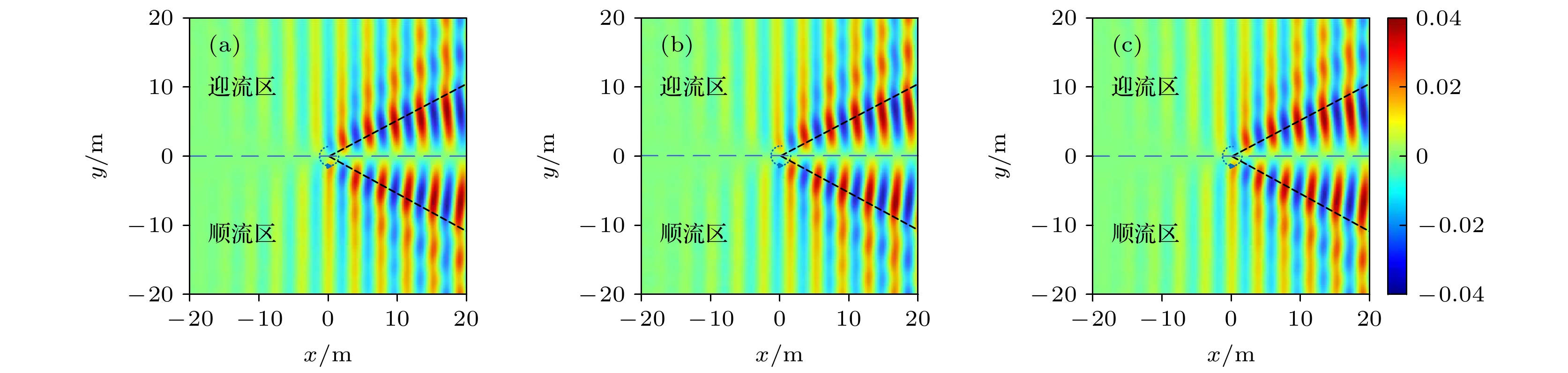
$ M{a_{{\text{ste}}}} = 0.005{\text{ }}M{a_{{\text{osc}}}} = 0.000625 $ 时不同时刻散射声压云图 (a)$ t = {T_{{\text{osc}}}} $ ; (b)$ t = 1.25{T_{{\text{osc}}}} $ ; (c)$ t = 1.5{T_{{\text{osc}}}} $ Fig. 7. Scattering sound contours of
$ M{a_{{\text{ste}}}} = 0.005{\text{ }}M{a_{{\text{osc}}}} = 0.000625 $ at different time: (a)$ t = {T_{{\text{osc}}}} $ ; (b)$ t = 1.25{T_{{\text{osc}}}} $ ; (c)$ t = 1.5{T_{{\text{osc}}}} $ .
图 6
$ M{a_{{\text{ste}}}} = 0.005{\text{ }}M{a_{{\text{osc}}}} = 0 $ 时, 不同时刻散射声压云图 (a)$ t = {T_{{\text{osc}}}} $ ; (b)$ t = 1.25{T_{{\text{osc}}}} $ ; (c)$ t = 1.5{T_{{\text{osc}}}} $ Fig. 6. Scattering sound contours of
$ M{a_{{\text{ste}}}} = 0.005{\text{ }}M{a_{{\text{osc}}}} = 0 $ at different times: (a)$ t = {T_{{\text{osc}}}} $ ; (b)$ t = 1.25{T_{{\text{osc}}}} $ ; (c)$ t = 1.5{T_{{\text{osc}}}} $ .
图 8
$ M{a_{{\text{ste}}}} = 0.005{\text{ }}M{a_{{\text{osc}}}} = 0.0025 $ 不同时刻散射声压云图 (a)$ t = {T_{{\text{osc}}}} $ ; (b)$ t = 1.25{T_{{\text{osc}}}} $ ; (c)$ t = 1.5{T_{{\text{osc}}}} $ Fig. 8. Scattering sound contours of
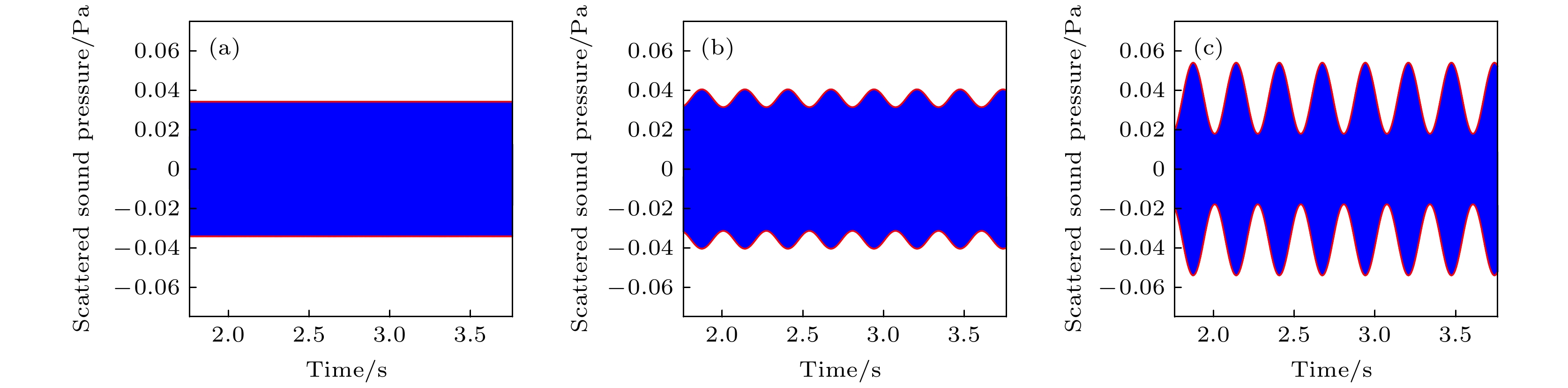
$ M{a_{{\text{ste}}}} = 0.005{\text{ }}M{a_{{\text{osc}}}} = 0.0025 $ at different times: (a)$ t = {T_{{\text{osc}}}} $ ; (b)$ t = 1.25{T_{{\text{osc}}}} $ ; (c)$ t = 1.5{T_{{\text{osc}}}} $ .
图 9 定常涡流场与振荡涡流场散射声压时域图 (a)
$ M{a_{{\text{ste}}}} = 0.005{\text{ }}M{a_{{\text{osc}}}} = 0 $ ; (b)$ M{a_{{\text{ste}}}} = 0.005{\text{ }}M{a_{{\text{osc}}}} = 0.000625 $ ; (c)$ M{a_{{\text{ste}}}} = 0.005{\text{ }}M{a_{{\text{osc}}}} = 0.0025 $ Fig. 9. Time domain diagram of scattering sound of steady vortex flow field and oscillating vortex flow field: (a)
$ M{a_{{\text{ste}}}} = $ $ 0.005{\text{ }}M{a_{{\text{osc}}}} = 0 $ ; (b)$ M{a_{{\text{ste}}}} = 0.005{\text{ }}M{a_{{\text{osc}}}} = 0.000625 $ ; (c)$ M{a_{{\text{ste}}}} = 0.005{\text{ }}M{a_{{\text{osc}}}} = 0.0025 $ .
图 10 定常涡流场与振荡涡流场散射声压频域图
Fig. 10. Frequency domain diagram of scattering sound of steady vortex flow field and oscillating vortex flow field.
图 11 不同入射声波频率散射指向性图
Fig. 11. Scattering directivity of different incident sound frequencies.
图 12 不同入射声波频率
$ t = {T_{{\text{osc}}}} $ 时刻散射声压云图 (a) f/F = 50; (b) f/F = 100; (c) f/F = 200Fig. 12. Scattering sound contours of different incident sound frequencies at
$ t = {T_{{\text{osc}}}} $ : (a) f/F = 50; (b) f/F = 100; (c) f/F = 200.
图 13 不同入射声波频率散射声压时域图 (a) f/F = 50; (b) f/F = 100; (c) f/F = 200
Fig. 13. Time domain diagram of scattering sound of different incident sound frequencies: (a) f/F = 50; (b) f/F = 100; (c) f/F = 200.
图 14 不同入射声波频率散射声压频域图 (a) f/F = 50; (b) f/F = 100; (c) f/F = 200
Fig. 14. Frequency domain diagram of scattering sound of different incident sound frequencies: (a) f/F = 50; (b) f/F = 100; (c) f/F = 200
图 15 散射强度和散射调制强度随入射声波频率变化规律
Fig. 15. The variation of scattering filed intensity and scattering modulating filed intensity of different incident sound frequencies.
图 16 不同涡流场振荡频率散射指向性图
Fig. 16. Scattering directivity of different vortex flow field oscillation frequencies.
图 17 不同涡流场振荡频率
$ t = {T_{{\text{osc}}}} $ 时刻散射声压云图 (a) f/F = 50; (b) f/F = 100; (c) f/F = 200Fig. 17. Scattering sound contours of different vortex flow field oscillation frequencies at
$ t = {T_{{\text{osc}}}} $ : (a) f/F = 50; (b) f/F = 100; (c) f/F = 200.
图 18 不同涡流场振荡频率散射声压时域图 (a) f/F = 50; (b) f/F = 100; (c) f/F = 200
Fig. 18. Time domain diagram of scattering sound of different vortex flow field oscillation frequencies: (a) f/F = 50; (b) f/F = 100; (c) f/F = 200.
图 19 不同涡流场振荡频率散射声压频域图 (a) f/F = 50; (b) f/F = 100; (c) f/F = 200
Fig. 19. Frequency domain diagram of scattering sound of different vortex flow field oscillation frequencies: (a) f/F = 50; (b) f/F = 100; (c) f/F = 200.
图 20 不同马赫数散射指向性图 (a)
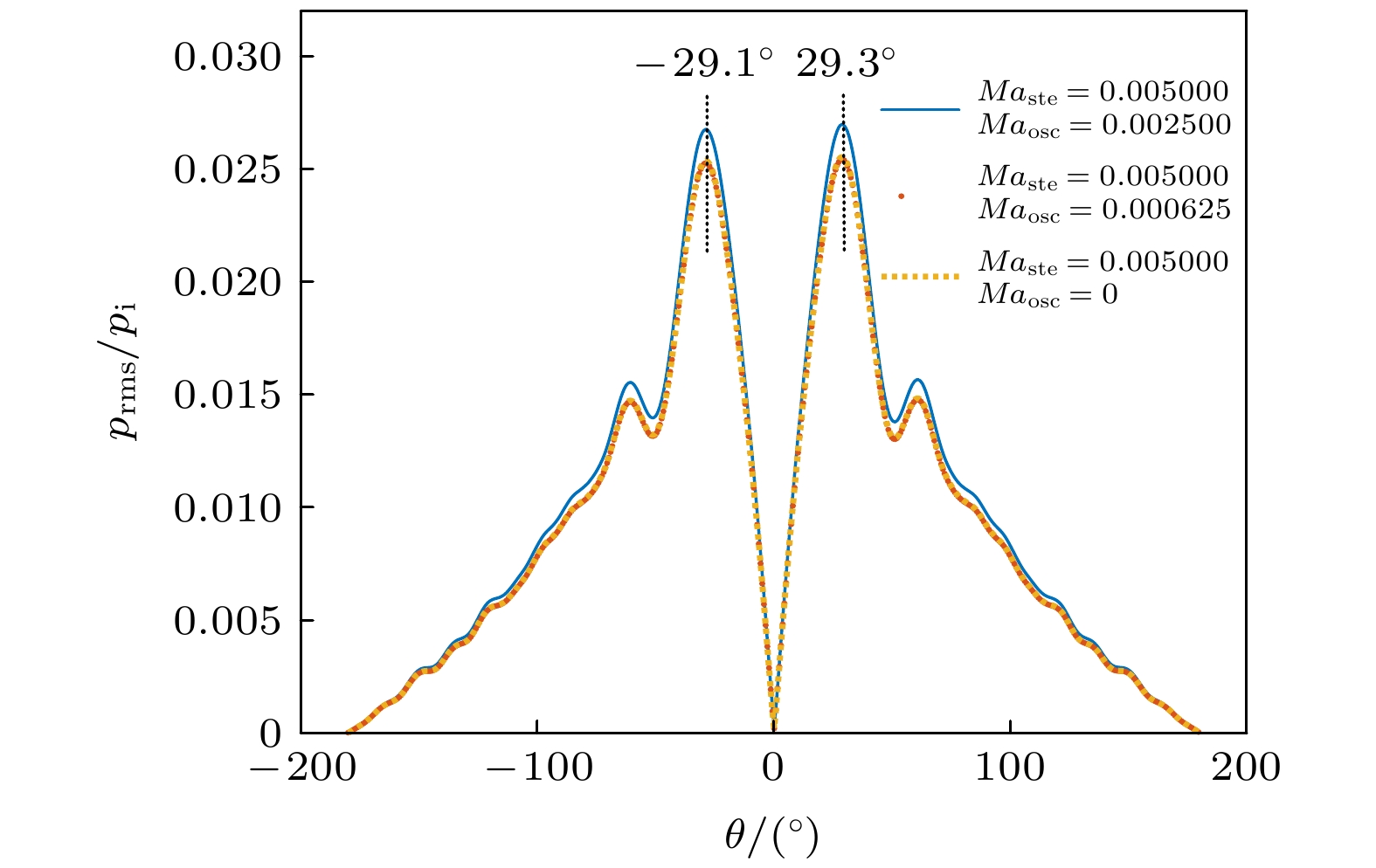
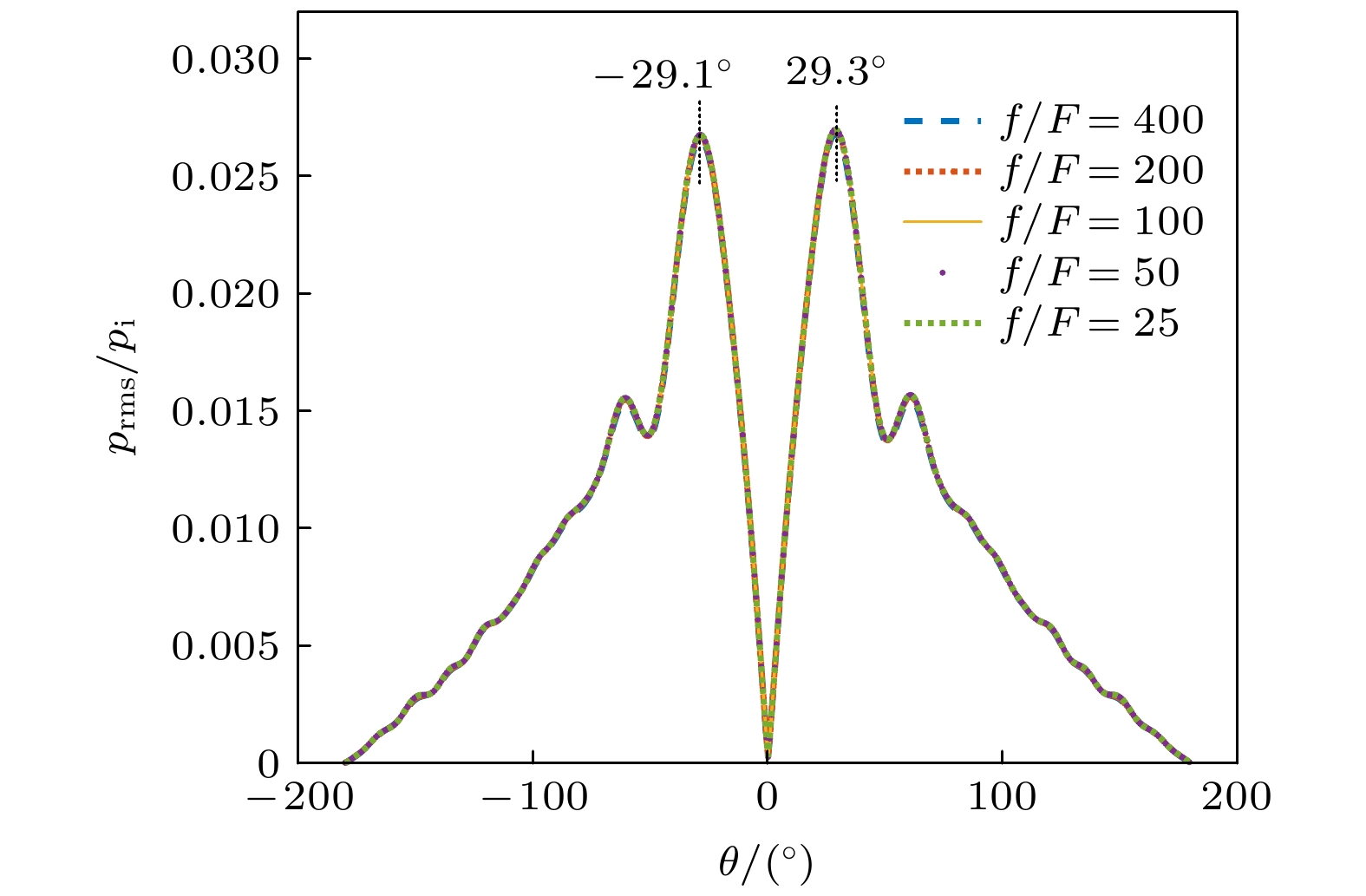
$ M{a_{{\text{ste}}}} = 0.005—0.04, M{a_{{\text{osc}}}} = 0.0025 $ ; (b)$M{a_{{\text{ste}}}} = 0.005, $ $ M{a_{{\text{osc}}}} = 0.0003125—0.0025$ Fig. 20. Scattering directivity of different Mach numbers: (a)
$M{a_{{\text{ste}}}} = 0.005-0.04, M{a_{{\text{osc}}}} = 0.0025$ ; (b)$M{a_{{\text{ste}}}} = 0.005, $ $ M{a_{{\text{osc}}}} = 0.0003125-0.0025$ .
图 21 不同马赫数振荡涡流场
$ t = {T_{{\text{osc}}}} $ 时刻散射声压云图 (a)$ M{a_{{\text{ste}}}} = 0.01 M{a_{{\text{osc}}}} = 0.0025 $ ; (b)$ M{a_{{\text{ste}}}} = 0.005{\text{ }}M{a_{{\text{osc}}}} = 0.0025 $ ; (c)$ M{a_{{\text{ste}}}} = 0.005{\text{ }}M{a_{{\text{osc}}}} = 0.00125 $ Fig. 21. Scattering sound contours of different Mach number at
$ t = {T_{{\text{osc}}}} $ : (a)$ M{a_{{\text{ste}}}} = 0.01 M{a_{{\text{osc}}}} = 0.0025 $ ; (b)$M{a_{{\text{ste}}}} = $ $ 0.005{\text{ }}M{a_{{\text{osc}}}} = 0.0025$ ; (c)$ M{a_{{\text{ste}}}} = 0.005{\text{ }}M{a_{{\text{osc}}}} = 0.00125 $ .
图 22
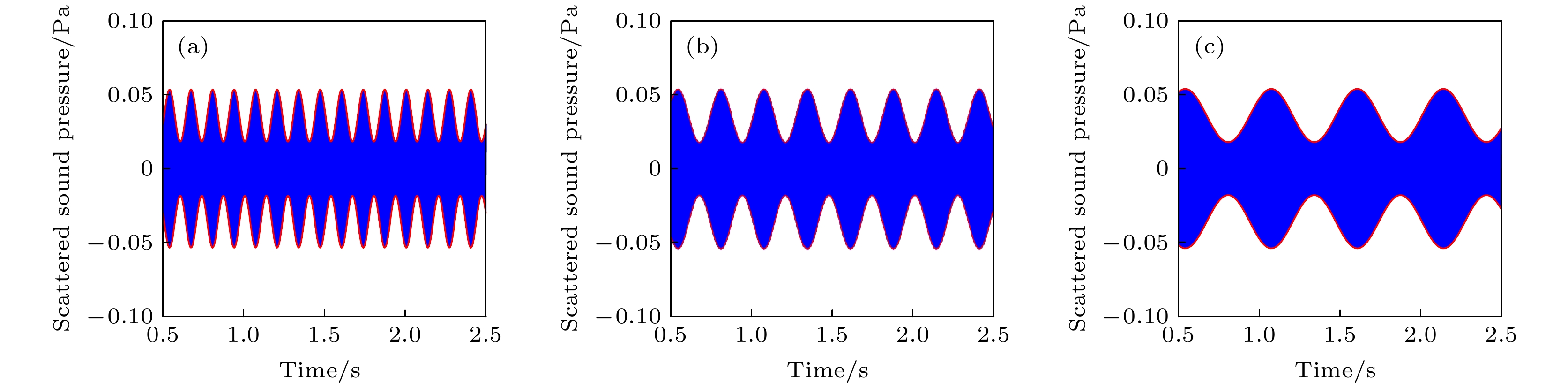
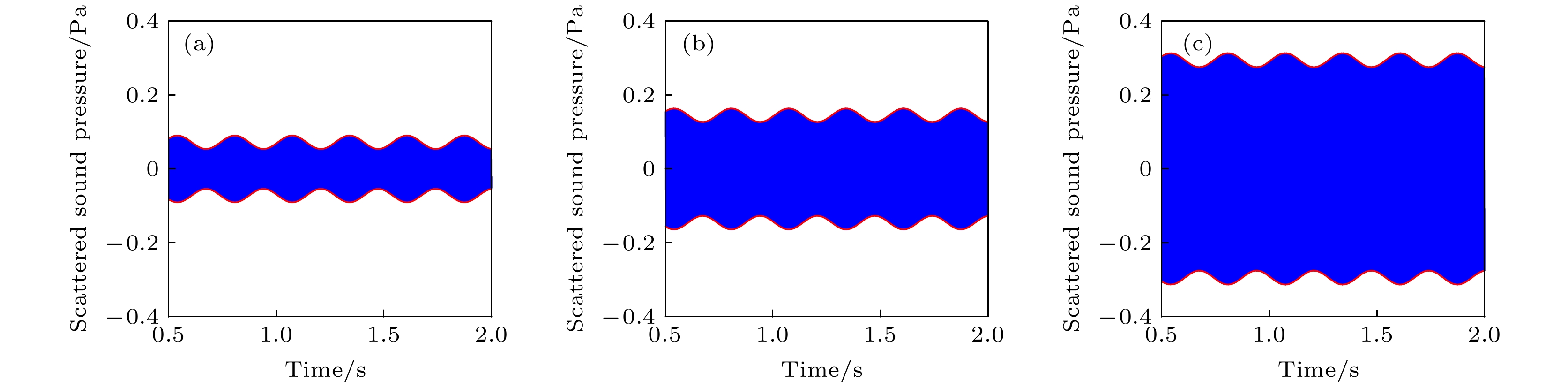
$ M{a_{{\text{osc}}}} = 0.0025 $ , 不同$ M{a_{{\text{ste}}}} $ 散射声压时域图 (a)$ M{a_{{\text{ste}}}} = 0.01 $ ; (b)$ M{a_{{\text{ste}}}} = 0.02 $ ; (c)$ M{a_{{\text{ste}}}} = 0.04 $ Fig. 22.
$ M{a_{{\text{osc}}}} = 0.0025 $ , time domain diagram of scattering sound of different$ M{a_{{\text{ste}}}} $ : (a)$ M{a_{{\text{ste}}}} = 0.01 $ ; (b)$ M{a_{{\text{ste}}}} = 0.02 $ ; (c)$ M{a_{{\text{ste}}}} = 0.04 $ .
图 23
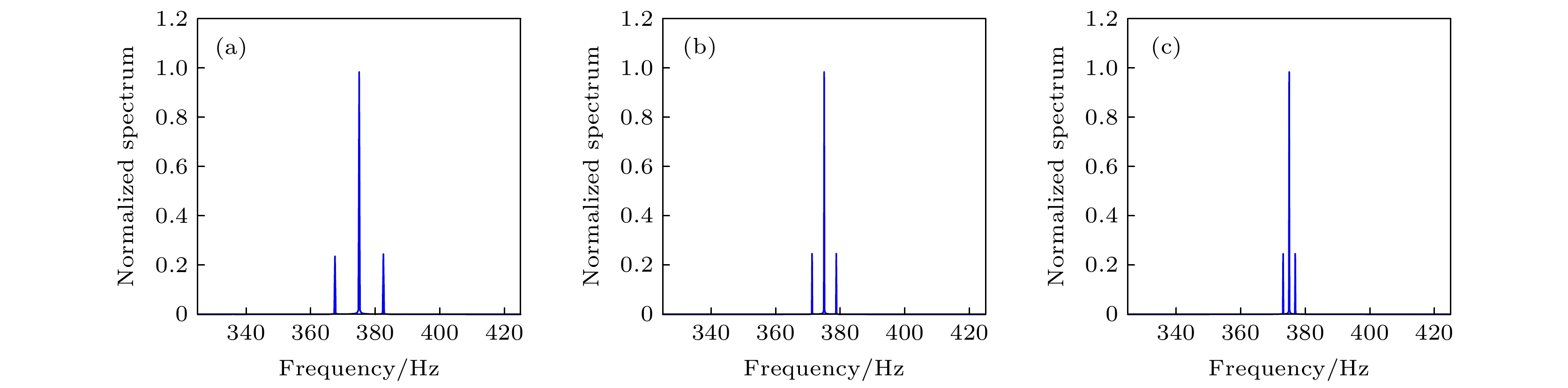
$ M{a_{{\text{osc}}}} = 0.0025 $ , 不同$ M{a_{{\text{ste}}}} $ 散射声压频域图 (a)$ M{a_{{\text{ste}}}} = 0.01 $ ; (b)$ M{a_{{\text{ste}}}} = 0.02 $ ; (c)$ M{a_{{\text{ste}}}} = 0.04 $ Fig. 23.
$ M{a_{{\text{osc}}}} = 0.0025 $ , frequency domain diagram of scattering sound of different$ M{a_{{\text{ste}}}} $ : (a)$ M{a_{{\text{ste}}}} = 0.01 $ ; (b)$ M{a_{{\text{ste}}}} = 0.02 $ ; (c)$ M{a_{{\text{ste}}}} = 0.04 $ .
图 24
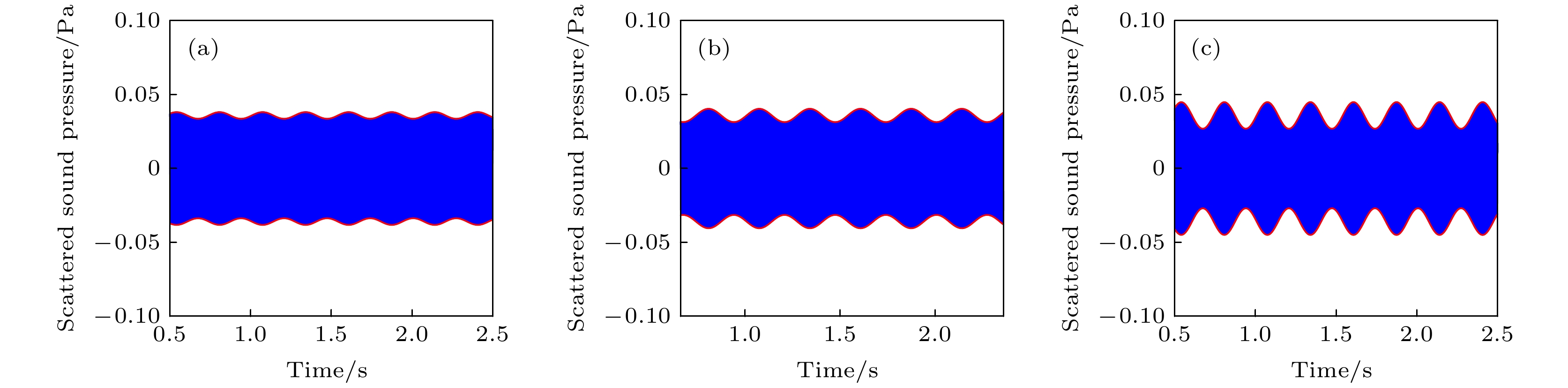
$ M{a_{{\text{ste}}}} = 0.005 $ , 不同$ M{a_{{\text{osc}}}} $ 散射声压时域图 (a)$ M{a_{{\text{osc}}}} = 0.0003125 $ ; (b)$ M{a_{{\text{osc}}}} = 0.000625 $ ; (c)$ M{a_{{\text{osc}}}} = 0.00125 $ Fig. 24.
$ M{a_{{\text{ste}}}} = 0.005 $ , time domain diagram of scattering sound of different$ M{a_{{\text{osc}}}} $ : (a)$ M{a_{{\text{osc}}}} = 0.0003125 $ ; (b)$M{a_{{\text{osc}}}} = $ $ 0.000625$ ; (c)$ M{a_{{\text{osc}}}} = 0.00125 $ .
图 25
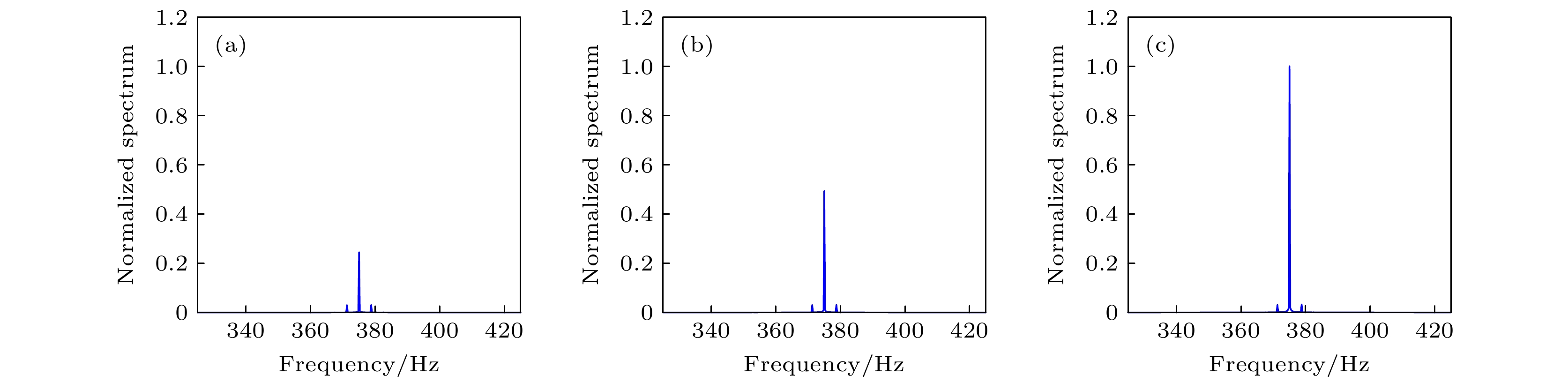
$ M{a_{{\text{ste}}}} = 0.005 $ , 不同$ M{a_{{\text{osc}}}} $ 散射声压频域图 (a)$ M{a_{{\text{osc}}}} = 0.0003125 $ ; (b)$ M{a_{{\text{osc}}}} = 0.000625 $ ; (c)$ M{a_{{\text{osc}}}} = 0.00125 $ Fig. 25.
$ M{a_{{\text{ste}}}} = 0.005 $ , frequency domain diagram of scattering sound of different$ M{a_{{\text{osc}}}} $ : (a)$ M{a_{{\text{osc}}}} = 0.0003125 $ ; (b)$M{a_{{\text{osc}}}} = $ $ 0.000625$ ; (c)$ M{a_{{\text{osc}}}} = 0.00125 $ .
图 26 散射声场强度和散射调制声场强度随
$ M{a_{{\text{ste}}}} $ (a)和$ M{a_{{\text{osc}}}} $ (b)变化规律Fig. 26. The variation of scattering filed intensity and scattering modulating filed intensity of different
$ M{a_{{\text{ste}}}} $ (a)and$ M{a_{{\text{osc}}}} $ (b).
图 28 不同涡核尺度
$ t = {T_{{\text{osc}}}} $ 时刻散射声压云图 (a) L = 0.5 m; (b) L = 1 m; (c) L = 2 mFig. 28. Scattering sound pressure contours of different vortex core scales at
$t = {T_{{\text{osc}}}}$ :(a) L = 0.5 m; (b) L = 1 m; (c) L = 2 m.
图 29 不同涡核尺度散射声压时域图 (a) L = 0.5 m; (b) L = 1 m; (c) L = 2 m
Fig. 29. Time domain diagram of scattering sound pressure of different vortex core scales: (a) L = 0.5 m; (b) L = 1 m; (c) L = 2 m.
图 30 不同涡核尺度散射声压频域图 (a) L = 0.5 m; (b) L = 1 m; (c) L = 2 m
Fig. 30. Frequency domain diagram of scattering sound pressure of different vortex core scales: (a) L = 0.5 m; (b) L = 1 m; (c) L = 2 m.
图 31 散射声场强度和散射调制声场强度随涡核尺度变化规律
Fig. 31. The variation of scattering field intensity and scattering modulating field intensity of different vortex core scales.
-
[1] Ostashev V E, Wilson D K 2015 Acoustics in Moving Inhomogeneous Media (New York: CRC Press) pp1–23
[2] Aurégan Y, Maurel A, Pagneux V 2008 Sound-Flow Interactions (Berlin: Springer) pp112–158
[3] Chakraborty P, Balachandar S, Adrian R J 2005 J. Fluid Mech. 535 189
Google Scholar
[4] Clair V, Gabard G 2018 J. Fluid Mech. 841 50
Google Scholar
[5] Colonius T, Lele S K, Moin P 1994 J. Fluid Mech. 260 271
Google Scholar
[6] Karabasov S, Kopiev V, Goloviznin V 2009 Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference) Miami, USA, May 10–12, 2009
[7] 马瑞轩, 王益民, 张树海, 武从海, 王勋年 2021 70 104301
Google Scholar
Ma R X, Wang Y M, Zhang S H, Wu C H, Wang X N 2021 Acta Phys. Sin. 70 104301
Google Scholar
[8] 王益民, 马瑞轩, 武从海, 罗勇, 张树海 2021 79 194302
Google Scholar
Wang Y M, Ma R X, Wu C H, Luo Y, Zhang S H 2021 Acta Phys. Sin. 79 194302
Google Scholar
[9] Semenov A G. 2017 Ultra Low Frequency Fields of Moving Bodies (New York: Nova Science Publishers) pp118–141
[10] Catalano P, Wang M, Iaccarino G 2003 Int. J. Heat Fluid Fl. 24 463
Google Scholar
[11] Zdravkovich M M 1997 Flow Around Circular Cylinders: Volume 2: Applications (Oxford: Oxford University Press) pp163–201
[12] Lighthill M J 1953 Proc. Cambridge Philos. Soc. 49 531
Google Scholar
[13] Kraichnan R H 1953 J. Acoust. Soc. Am. 25 1096
Google Scholar
[14] Bogey C, Bailly C, Juve D 2002 AIAA J. 40 235
Google Scholar
[15] Bailly C, Juve D 2000 AIAA J. 38 22
Google Scholar
[16] Pierce A D. 2019 Acoustics: An Introduction to Its Physical Principles and Applications (East Sandwich: Springer) pp427– 480
[17] Pierce A D 1990 J. Acoust. Soc. Am. 87 2292
Google Scholar
[18] Cheinet S, Ehrhardt L, Juve D, Benon B P 2012 J. Acoust. Soc. Am. 132 2198
Google Scholar
[19] Cockburn B, Shu C W 2001 J. Sci. Comput. 16 173
Google Scholar
[20] Cockburn B, Shu C W 1989 Math. Comp. 52 411
Google Scholar
[21] Lee H D, Kwon O J 2013 J. Mech. Sci. Technol. 27 3331
Google Scholar
[22] Williamschen M, Gabard G J 2020 AIAA J. 58 1079
Google Scholar
[23] 程建春 2019 声学原理(第二版下卷) (北京: 科学出版社) 第969页
Cheng J C 2012 Acoustic principles (Volume II of the Second Edition) (Beijing: Science Press) p969 (in Chinese)
[24] 冯士筰, 李凤岐, 李少菁 1999 海洋科学导论 (北京: 高等教育出版社) 第181页
Feng S Z, Li F Q, Li S J 1999 Introduction to Marine Science (Beijing: Higher Education Press) p181 (in Chinese)
[25] 杜浩, 熊鳌魁, 张咏鸥 2020 声学学报 45 55
Google Scholar
Du H, Xiong A K, Zhang Y O 2020 Acta Acoust. 45 55
Google Scholar
[26] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics (New York: Springer) pp531– 610
[27] Headrick R H, Lynch J F, Kemp J N, Newhall A E, Heydt K 2000 J. Acoust. Soc. Am. 107 201
Google Scholar
[28] Ford R, Smith S G L 1999 J. Fluid Mech. 386 305
Google Scholar
[29] Fetter A L 1964 Phys. Rev. A 136 1488
Google Scholar
下载:
计量
- 文章访问数: 4673
- PDF下载量: 125
- 被引次数: 0
