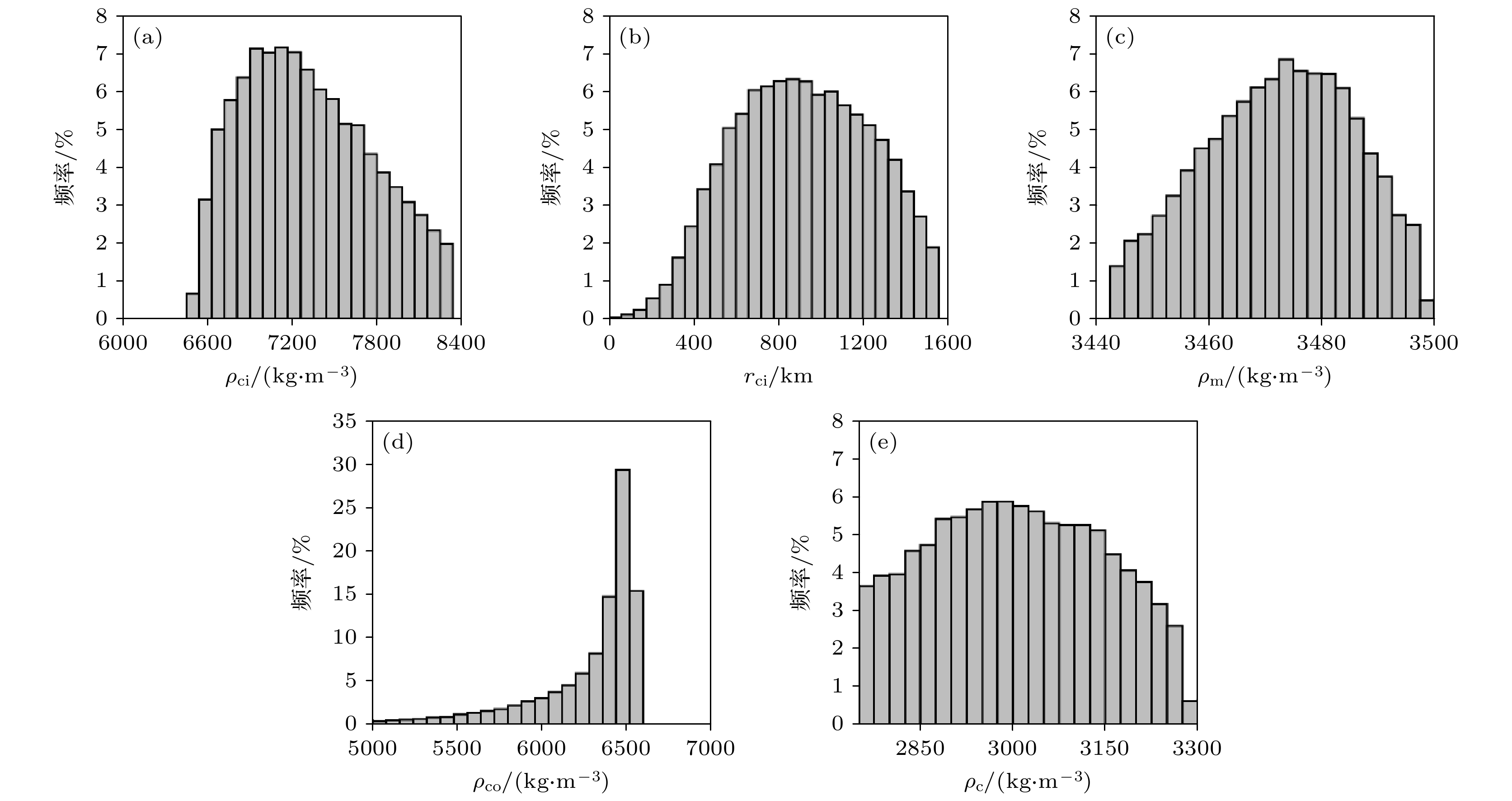
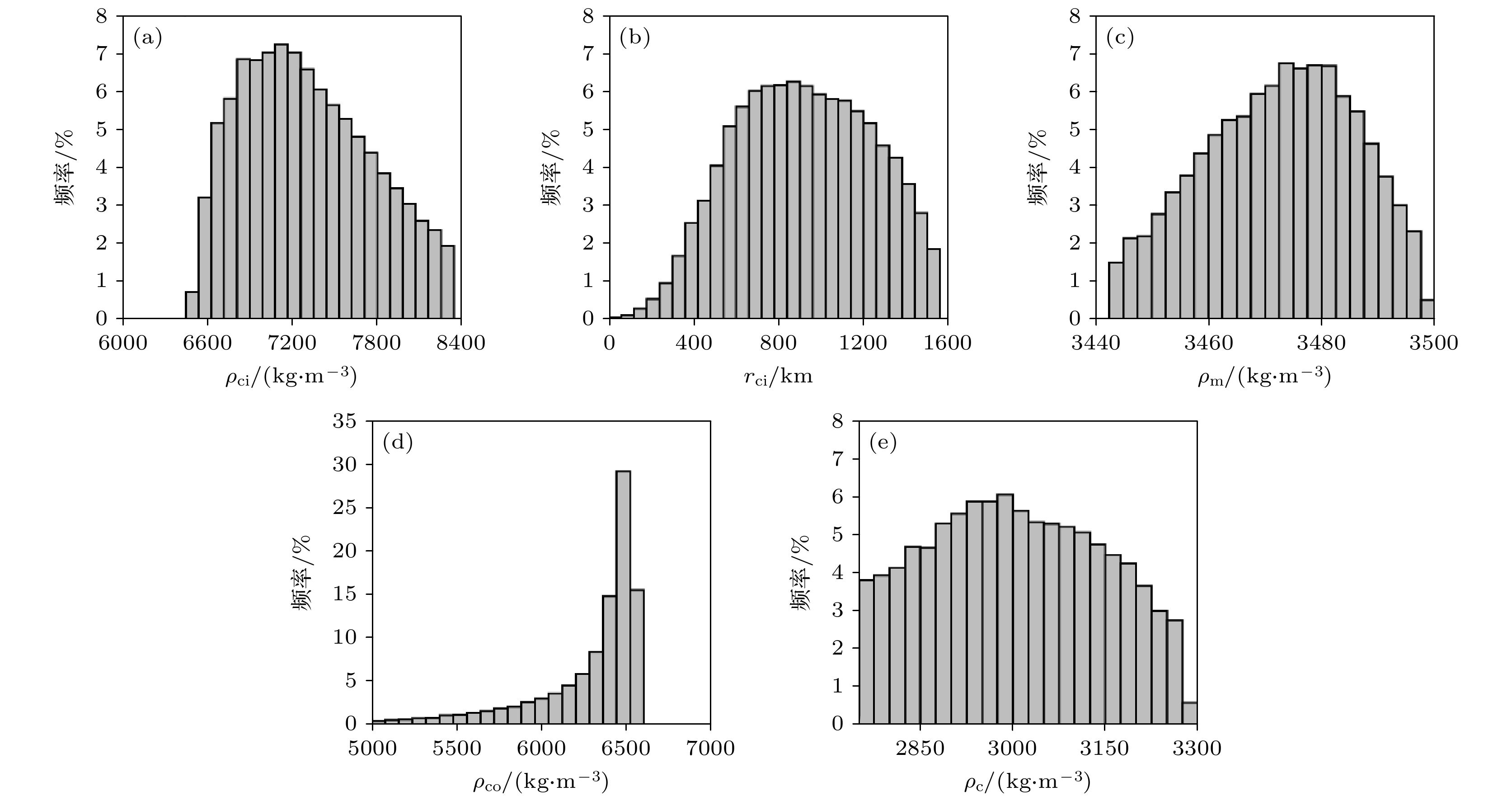
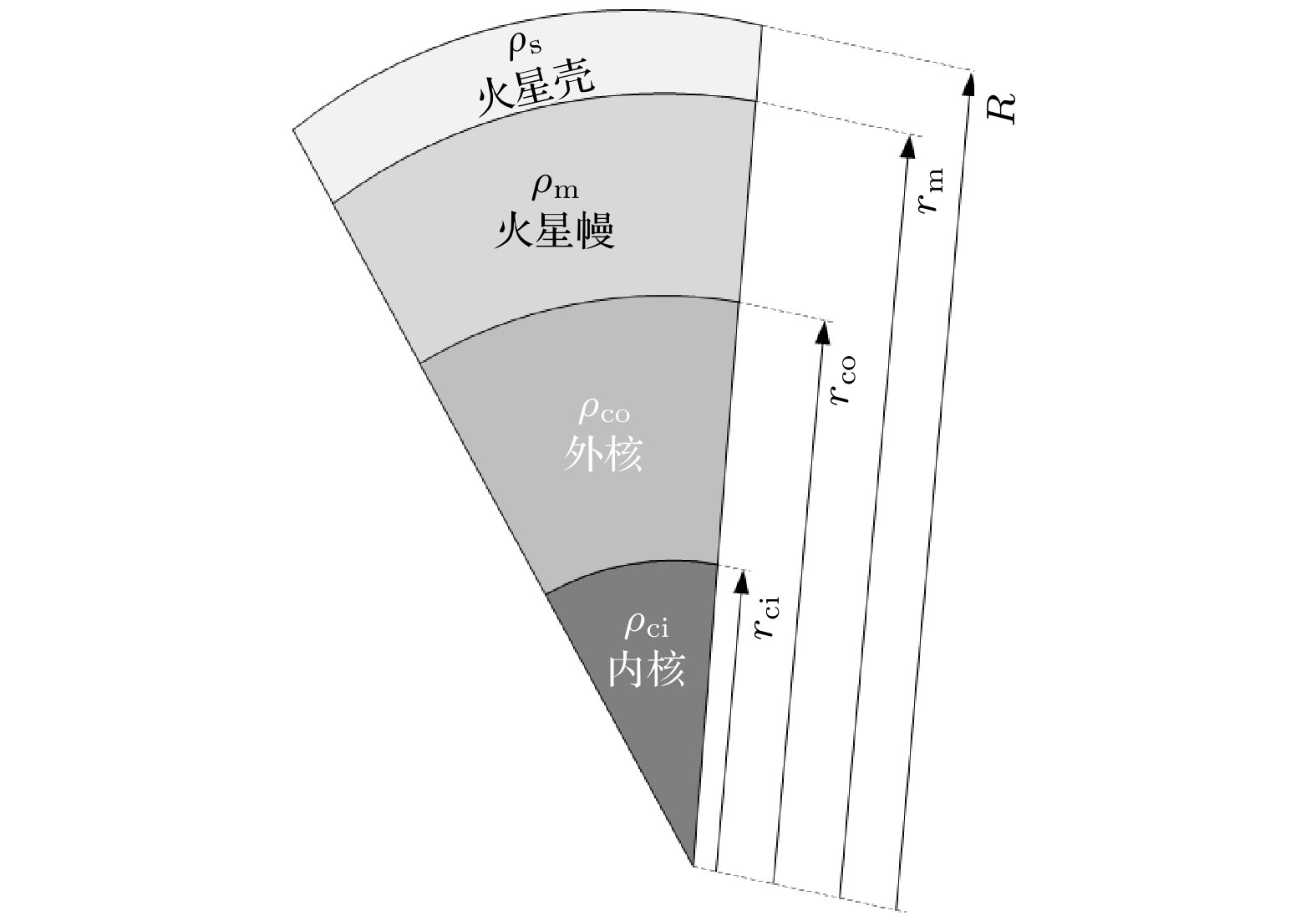
-
针对当前InSight数据无法检测火星固态内核是否存在的问题, 提出利用火星平均密度和平均惯性矩因子估算火星固态内核的大小及其密度组成. 根据火星高阶重力场模型JGMRO120f和GMM3-120以及最新火星岁差率, 推导了观测数据下的火星平均密度和平均惯性矩因子; 参考火星内部结构的4层模型以及不同自由参数(壳层密度、幔层密度、外核密度、内核大小和内核密度), 求解了火星平均密度和平均惯性矩因子的模型值. 利用观测值与模型值最小残差平方和作为约束条件, 大批量统计结果表明: 1)两个重力场模型求解的自由参数具有相同的分布特征, 自由参数的最优值基本一致; 2)火星壳层密度、幔层密度和外核密度接近其他研究结果, 表明统计结果有一定的参考价值; 3)火星可能存在840 km左右的固态内核, 其密度约为6950 kg⋅m–3. 内核密度大小表明火星内核不由纯铁物质组成, 该结果与火星核富集轻元素物质的近期研究一致, 计算结果具有一定的参考价值. 由于反演结果的非唯一性, 未来随着InSight火星星震数据处理技术的提高, 有望进一步约束火星内核的大小及其组成.It is still difficult to detect the existence of Martian solid inner core merely based on Mars seismic InSight data. To deal with this problem, our study intends to use the mean density and mean moment of inertia factor to constrain the size and density of Martian solid inner core. Using the Mars high-degree gravity field models: JGMRO120f and GMM3-120, and considering the recent precession rate, we obtain the mean density and mean moment of inertia factor, which are treated as the observed values. Referring to the 4-layers internal structure model of Mars, and considering the 4 parameters, i.e. crustal density, mantle density, density of outer core, size and density of inner core, we calculate the modeled values of the Martian mean density and the mean moment of inertia factor. From the minimum residuals between observed and modeled values of mean density as well as that of mean moment of inertia factor, it is found that the two gravity field models have the same result of distribution of free parameters. As to the optimized values of the free parameters, the two gravity field models even have the same results. Furthermore, the optimized crustal density, mantel density and density of outer core approach other studies, indicating the dependence of our results. Finally, our result demonstrates that Mars likely has a solid inner core with a size close to 840 km, and the density of inner core is nearly 6950 kg⋅m–3. Our result implies that Mars has an inner core not fully composed of pure iron, which is consistent with the recent study that Mars requires a substantial complement of light elements in Martian core. However, it is further needed to constrain the size and composition of Martian inner core due to the non-uniqueness of inversion results. With the improvement of processing technology on the InSight data, it can be further constrained for the size and composition of Martian inner core.
-
Keywords:
- InSight /
- precession rate /
- mean moment of inertia factor /
- size of Martian inner core /
- density of Martian inner core
[1] Mittelholz A, Johnson C L, Feinberg J M, Langlais B, Phillips R J 2020 Sci. Adv. 6 eaba0513
Google Scholar
[2] Stevenson D J 2001 Natrue 412 214
Google Scholar
[3] Taylor G J 2013 Geochemistry 73 401
Google Scholar
[4] Plesa A C, Tosi N, Grott M, Breuer D 2015 J. Geophys. Res. Planet 120 995
Google Scholar
[5] Khan A, Liebske C, Rozel A, Rivoldini A, Nimmo F, Connolly J A D, Plesa A C, Giardini D A 2018 J. Geophys. Res. Planet 123 575
Google Scholar
[6] Bagheri A, Khan A, Al‐Attar D, Crawford O, Giardini D 2019 J. Geophys. Res. Planet 124 2703
Google Scholar
[7] Genova A, Goossens S, Lemoine F G, Mazarico E, Neumann G A, Smith D E, Zuber M T 2016 Icarus 272 228
Google Scholar
[8] Konopliv A S, Park R S, Folkner W M 2016 Icarus 274 253
Google Scholar
[9] Rivoldini A, Van Hoolst T, Verhoeven O, Mocquet A, Dehant V 2011 Icarus 213 451
Google Scholar
[10] Konopliv A S, Park R S, Rivoldini A, Baland R M, Maistre S L, Hoolst T V, Yseboodt M, Dehant V 2020 Geophys Res. Lett. 47 e2020GL090568
Google Scholar
[11] Stähler S C, Khan A, Banerdt W B, et al. 2021 Science 373 443
Google Scholar
[12] Sohl F, Schubert G, Spohn T 2005 J. Geophys. Res. Planet 110 E12008
Google Scholar
[13] Kahan D S, Folkner W M, Buccino D R, Dehant V, Maistre S L, Rivoldini A, Hoolst T V, Yseboodt M, Marty J C 2021 Planet. Space Sci. 199 105208
Google Scholar
[14] Konopliv A S, Asmar S W, Folkner W M, Karatekin Ö, Nunes D C, Smrekar S E, Yoder C F, Zuber M T 2011 Icarus 211 401
Google Scholar
[15] Ding M, Lin J, Gu C, Huang Q H, Zuber M T 2019 J. Geophys. Res. Planet 124 3095
Google Scholar
[16] Zhong Z, Yan J, Liu X, Chen S, Fan G, Yang C, Pang L, Barriot J P 2022 Icarus 374 114741
Google Scholar
[17] Planetary Data System https://pds-geosciences.wustl.edu/default.htm [2020.10.23]
[18] Gerald S 2015 Treatise on Geophysics (Oxford: Elsevier) pp153–193
[19] Goossen S, Sabaka T J, Genova A, Mazarico E, Nicholas J B, Neumann G A 2017 Geophys Res. Lett. 44 7686
Google Scholar
[20] Tiesinga E, Mohr P J, Newell D B, Taylor B N 2021 J. Phys. Chem. Ref. Data 50 033105
Google Scholar
[21] Zuber M T, Smith D E 1997 J. Geophys. Res. Planet 102 28673
Google Scholar
[22] Baland R M, Yseboodt M, Maistre S L, Rivoldini A, Hoolst T V, Dehant V 2020 Celest. Mech. Dyn. Astr. 132 1
Google Scholar
[23] Knapmeyer-Endrun B, Panning M P, Bissig F, et al. 2021 Science 373 438
Google Scholar
[24] Yan J, Xu L, Li F, Matsumoto K, Rodriguez J A P, Miyamoto H, Dohm J M 2015 Adv. Space Res. 55 1721
Google Scholar
[25] 钟振, 张腾, 段炼, 李毅, 朱化强 2021 武汉大学学报-信息科学版 46 238
Google Scholar
Zhong Z, Zhang T, Duan L, Li Y, Zhu H Q 2021 Geomat. Inform. Sci. Wuhan Univ. 46 238
Google Scholar
[26] Steenstra E S, Westrenen W V 2018 Icarus 315 69
Google Scholar
[27] Semprich J, Filiberto J 2020 Meteorit. Planet. Sci. 55 1600
Google Scholar
[28] McGetchin T R, Smith J R 1978 Icarus 34 512
Google Scholar
[29] Khan A, Sossi P A, Liebske C, Rivoldini A, Giardini D 2022 Earth Planet. Sc. Lett. 578 117330
Google Scholar
[30] Wieczorek M A, Zuber M T 2004 J. Geophys. Res. Planet 109 E01009
Google Scholar
[31] Wieczorek M A, Broquet A, McLennan S M, et al. 2022 J. Geophys. Res. Planet 127 e2022JE007298
Google Scholar
-
图 2 由重力场模型JGMRO120f推算的质量、平均惯性矩因子和二阶位系数反演的相关参数
Fig. 2. Parameters estimated from the calculated Martian mass, mean moment of inertia factor and gravitation coefficient of degree 2 of the gravity field model JGMRO120f.
图 3 由重力场模型GMM3-120推算的质量、平均惯性矩因子和二阶位系数反演的相关参数
Fig. 3. Parameters estimated from the calculated Martian mass, mean moment of inertia factor and gravitation coefficient of degree 2 of the gravity field model GMM3-120.
表 1 参数取值
Table 1. Values of the parameters used in calculation.
序号 参数 取值及范围 1 JGMRO120f模型的火星质量
M/kg与二阶位系数M = 6.417120511584593×1023, C20 = –0.8750219819894×10–3,
C22 = –0.8463283575906×10–4, S22 = 0.4893975901192×10–42 GMM3-120模型的火星质量
M/kg与二阶位系数M = 6.417120090587431×1023, C20 = –0.87502113235452894×10–3,
C22 = –0.84635903869414677×10–4, S22 = 0.48934625860229178×10–43 平均半径R/km 3389.5 4 平均密度$\bar{\rho }$/(kg⋅m–3) 3934.093 5 InSight数据的火星最新岁差率
$ \dot{\psi } $/(ms·a–1) [13]–7605 6 平均惯性矩因子${I}/({M{R}^{2} })$ 0.3637801121 (JGMRO120f), 0.3637797586 (GMM3-120) 
下载: 导出CSV
表 3 目标函数f对不同待求参数的敏感度S
Table 3. Sensitivity of various parameters S to the objective function f
敏感度S JGMRO120f GMM3-120 S(f, ρci) –11.1404 –11.1404 S(f, rci) –2.6496 –2.6496 S(f, ρm) –305.8501 –305.8642 S(f, ρco) –96.8772 –96.8782 S(f, ρc) –14.7235 –14.7245
下载: 导出CSV
-
[1] Mittelholz A, Johnson C L, Feinberg J M, Langlais B, Phillips R J 2020 Sci. Adv. 6 eaba0513
Google Scholar
[2] Stevenson D J 2001 Natrue 412 214
Google Scholar
[3] Taylor G J 2013 Geochemistry 73 401
Google Scholar
[4] Plesa A C, Tosi N, Grott M, Breuer D 2015 J. Geophys. Res. Planet 120 995
Google Scholar
[5] Khan A, Liebske C, Rozel A, Rivoldini A, Nimmo F, Connolly J A D, Plesa A C, Giardini D A 2018 J. Geophys. Res. Planet 123 575
Google Scholar
[6] Bagheri A, Khan A, Al‐Attar D, Crawford O, Giardini D 2019 J. Geophys. Res. Planet 124 2703
Google Scholar
[7] Genova A, Goossens S, Lemoine F G, Mazarico E, Neumann G A, Smith D E, Zuber M T 2016 Icarus 272 228
Google Scholar
[8] Konopliv A S, Park R S, Folkner W M 2016 Icarus 274 253
Google Scholar
[9] Rivoldini A, Van Hoolst T, Verhoeven O, Mocquet A, Dehant V 2011 Icarus 213 451
Google Scholar
[10] Konopliv A S, Park R S, Rivoldini A, Baland R M, Maistre S L, Hoolst T V, Yseboodt M, Dehant V 2020 Geophys Res. Lett. 47 e2020GL090568
Google Scholar
[11] Stähler S C, Khan A, Banerdt W B, et al. 2021 Science 373 443
Google Scholar
[12] Sohl F, Schubert G, Spohn T 2005 J. Geophys. Res. Planet 110 E12008
Google Scholar
[13] Kahan D S, Folkner W M, Buccino D R, Dehant V, Maistre S L, Rivoldini A, Hoolst T V, Yseboodt M, Marty J C 2021 Planet. Space Sci. 199 105208
Google Scholar
[14] Konopliv A S, Asmar S W, Folkner W M, Karatekin Ö, Nunes D C, Smrekar S E, Yoder C F, Zuber M T 2011 Icarus 211 401
Google Scholar
[15] Ding M, Lin J, Gu C, Huang Q H, Zuber M T 2019 J. Geophys. Res. Planet 124 3095
Google Scholar
[16] Zhong Z, Yan J, Liu X, Chen S, Fan G, Yang C, Pang L, Barriot J P 2022 Icarus 374 114741
Google Scholar
[17] Planetary Data System https://pds-geosciences.wustl.edu/default.htm [2020.10.23]
[18] Gerald S 2015 Treatise on Geophysics (Oxford: Elsevier) pp153–193
[19] Goossen S, Sabaka T J, Genova A, Mazarico E, Nicholas J B, Neumann G A 2017 Geophys Res. Lett. 44 7686
Google Scholar
[20] Tiesinga E, Mohr P J, Newell D B, Taylor B N 2021 J. Phys. Chem. Ref. Data 50 033105
Google Scholar
[21] Zuber M T, Smith D E 1997 J. Geophys. Res. Planet 102 28673
Google Scholar
[22] Baland R M, Yseboodt M, Maistre S L, Rivoldini A, Hoolst T V, Dehant V 2020 Celest. Mech. Dyn. Astr. 132 1
Google Scholar
[23] Knapmeyer-Endrun B, Panning M P, Bissig F, et al. 2021 Science 373 438
Google Scholar
[24] Yan J, Xu L, Li F, Matsumoto K, Rodriguez J A P, Miyamoto H, Dohm J M 2015 Adv. Space Res. 55 1721
Google Scholar
[25] 钟振, 张腾, 段炼, 李毅, 朱化强 2021 武汉大学学报-信息科学版 46 238
Google Scholar
Zhong Z, Zhang T, Duan L, Li Y, Zhu H Q 2021 Geomat. Inform. Sci. Wuhan Univ. 46 238
Google Scholar
[26] Steenstra E S, Westrenen W V 2018 Icarus 315 69
Google Scholar
[27] Semprich J, Filiberto J 2020 Meteorit. Planet. Sci. 55 1600
Google Scholar
[28] McGetchin T R, Smith J R 1978 Icarus 34 512
Google Scholar
[29] Khan A, Sossi P A, Liebske C, Rivoldini A, Giardini D 2022 Earth Planet. Sc. Lett. 578 117330
Google Scholar
[30] Wieczorek M A, Zuber M T 2004 J. Geophys. Res. Planet 109 E01009
Google Scholar
[31] Wieczorek M A, Broquet A, McLennan S M, et al. 2022 J. Geophys. Res. Planet 127 e2022JE007298
Google Scholar
下载:
计量
- 文章访问数: 4095
- PDF下载量: 62
- 被引次数: 0
