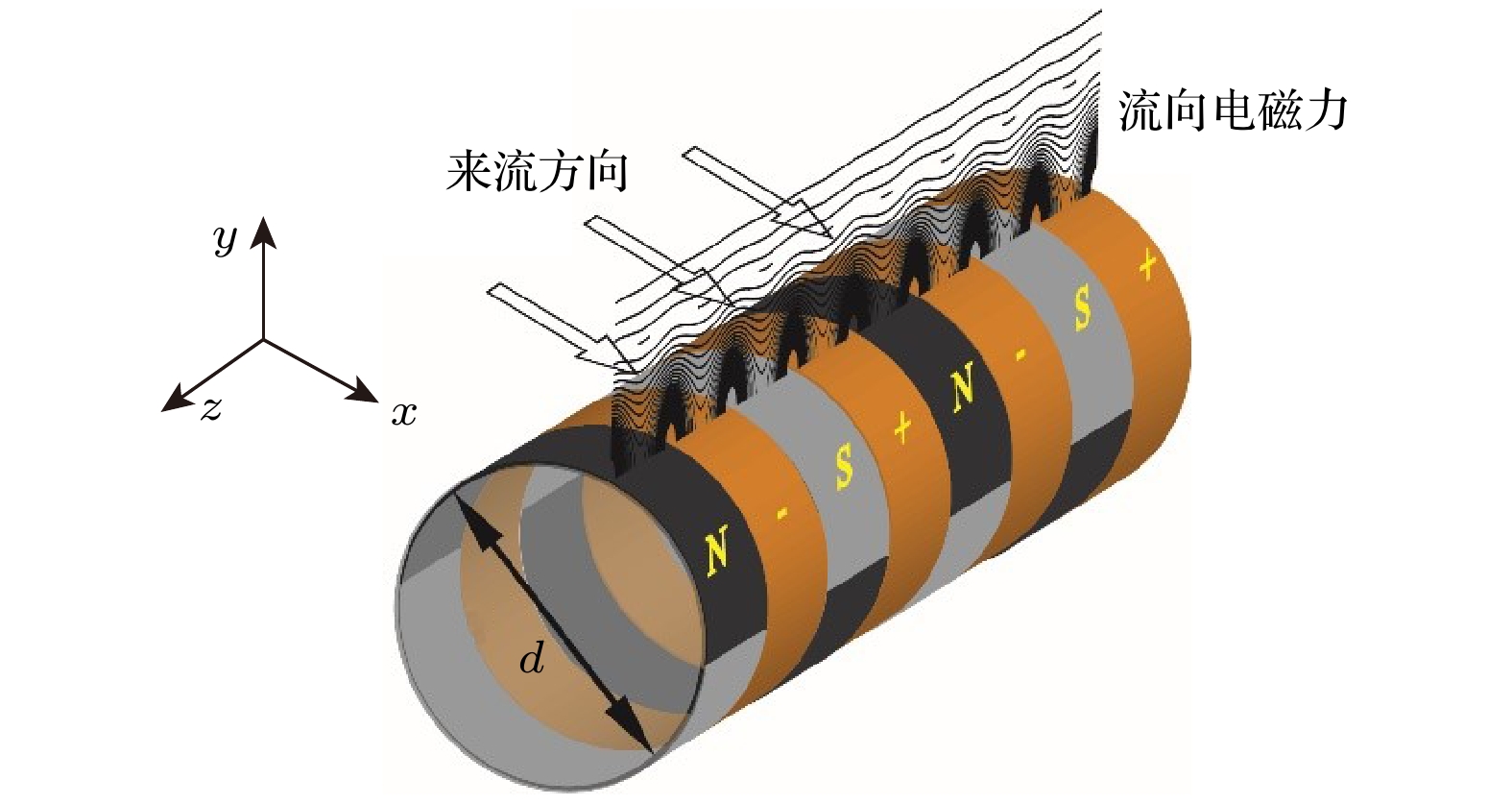
-
圆柱绕流是典型的振荡器流动, 扰动在空间固定位置随时间增长, 诱导尾迹转捩, 从而增大柱体振动与流场噪声. 本文通过在圆柱迎流面、背流面以及全圆柱表面放置电磁激活板产生流向电磁力, 调控二维基态流, 降低尾迹中扰动增长率, 实现转捩模态改变. Floquet稳定性分析发现, 迎流面控制中转捩模态A和B的增长率变化较小, 而背流面和全圆柱控制中两种模态的增长率均随电磁力控制参数的增大而减小. 分析椭圆不稳定和双曲不稳定诱导的无黏增长率发现, 迎流面控制中尾迹高无黏增长率与无控制时相似, 而背流面和全圆柱控制中均随电磁力作用参数的增大而减小. 三维直接数值模拟发现圆柱尾迹三维形态在背流面控制和全圆柱控制中由模态B转变为模态A, 与Floquet稳定性分析结果吻合. 此外, 当圆柱尾迹形态发生变化后, 背流面控制和全圆柱控制下圆柱所受的阻力分别降低了15.2%和14.4%.The flow around a cylinder is a typical flow acting as the oscillator, and the perturbations can grow with time at a fixed position. This phenomenon can induce the laminar-turbulent transition in the wake, thus increasing the vibrations of the cylinder as well as the noise in the flow system. There exist three control strategies, i.e. the streamwise Lorentz force from the electromagnetic actuator set on the windward surface named windward control, the leeward surface named leeward control, and the whole surface of cylinder named global control, which are adopted to modify the two-dimensional base flow, thereby reducing the growth rates of perturbations in the wake and changing the transition mode. According to the Floquet stability analysis, it is found that the growth rates of the transition modes A and B present small changes in the windward control, while the growth rates of the two modes decrease with the increase of the control number in the other two control cases. Comparing the inviscid growth rates induced by the elliptic instability and the hyperbolic instability with each other, it is observed that the high inviscid growth rate in the windward control can be similar to those without control, while the inviscid growth rates can decrease with the increase of control number in the other two control cases. Three-dimensional direct numerical simulations are performed to validate the control effects. The results shows that the three-dimensional shape of the wake is changed from mode B to mode A when the actuator is set on the leeward surface or the whole surface of the cylinder. This is consistent with the result from the Floquet stability analysis. In addition, the drag of the cylinder reduces 15.2% for the leeward control and 14.4% for the the global control.
-
Keywords:
- cylinder wake /
- streamwise Lorentz force /
- transition control /
- flow instability
[1] Williamson C H K 1996 Annu. Rev. Fluid. Mech. 28 477
Google Scholar
[2] Jackson C P 1987 J. Fluid Mech. 182 23
Google Scholar
[3] Barkley D, Henderson R D 1996 J. Fluid. Mech. 322 215
Google Scholar
[4] Jiang H Y, Cheng L 2020 Phys. Fluids 32 014103
Google Scholar
[5] McClure J, Pavan C, Yarusevych S 2019 Phys. Rev. Fluids 4 124702
Google Scholar
[6] Xu C, Mao Y J, Hu Z W 2019 Aerosp. Sci. Technol. 88 233
Google Scholar
[7] Gao D L, Huang Y W, Chen W L, Chen G B, Li H 2019 Phys. Fluids 31 057105
Google Scholar
[8] Del Guercio G, Cossu C, Pujals G 2014 J. Fluid Mech. 752 572
Google Scholar
[9] Xu F, Chen W L, Bai W F, Xiao Y Q, Qu J P 2017 Comput. Fluids 145 52
Google Scholar
[10] Mao X R, Sherwin S 2015 J. Fluid Mech. 775 241
Google Scholar
[11] 陈蒋力, 陈少强, 任峰, 胡海豹 2022 71 084701
Google Scholar
Chen J L, Chen S Q, Ren F, Hu H B 2022 Acta Phys. Sin. 71 084701
Google Scholar
[12] Li J C, Zhang M Q 2022 J. Fluid Mech. 932 A44
Google Scholar
[13] Marquet O, Sipp D, Jacquin L 2008 J. Fluid Mech. 615 221
Google Scholar
[14] Khodkar M A, Taira K 2020 J. Fluid Mech. 904 R1
Google Scholar
[15] Albrecht T, Stiller J, Metzkes H, Weier T, Gerbeth G 2013 Eur. Phys. J. Spec. Top. 220 275
Google Scholar
[16] Kim S, Lee C M 2001 Exp. Fluids 28 252
Google Scholar
[17] 尹纪富, 尤云祥, 李巍, 胡天群 2014 63 044701
Google Scholar
Yin J F, You Y X, Li W, Hu T Q 2014 Acta Phys. Sin. 63 044701
Google Scholar
[18] Zhang H, Fan B C, Chen Z H 2010 Eur. J. Mech. B-Fluids 29 53
Google Scholar
[19] Zhang H, Fan B C, Chen Z H, Li H Z 2014 J. Fluids Struct. 48 62
Google Scholar
[20] Zhang H, Liu M K, Han Y, Gui M Y, Li J, Chen Z H 2017 Comput. Fluids 159 112
Google Scholar
[21] 刘宗凯, 薄昱明, 王军, 崔珂 2017 66 084704
Google Scholar
Liu Z K, Bo Y M, Wang J, Cui K 2017 Acta Phys. Sin. 66 084704
Google Scholar
[22] Huang Y D, Zhou B M, Tang Z L 2017 Appl. Math. Mech. Engl. Ed. 38 439
Google Scholar
[23] Berger T W, Kim J, Lee C, Lim J 2000 Phys. Fluids 12 631
Google Scholar
[24] Du Y Q, Karniadakis G E 2000 Science 288 1230
Google Scholar
[25] Blackburn H M, Lee D, Albrecht T, Singh J 2019 Comput. Phys. Commun. 245 106804
Google Scholar
[26] Karniadakis G E, Israeli M, Orszag S A 1991 J. Comput. Phys. 97 414
Google Scholar
[27] Barkley D, Blackburn H M, Sherwin S J 2008 Int. J. Numer. Meth. Fluids 57 1435
Google Scholar
[28] Williamson C H K 1989 J Fluid Mech. 206 579
Google Scholar
[29] Hammache M, Gharib M 1991 J. Fluid Mech. 232 567
Google Scholar
[30] Thompsom M C, Leweke T, Williamson C H K 2001 J. Fluid Struct. 15 607
Google Scholar
[31] Jeong J, Hussain F 1995 J. Fluid Mech. 285 69
Google Scholar
-
图 3 随雷诺数变化的圆柱尾迹Strouhal数
Fig. 3. The Strouhal number of the cylinder wake varying with the Reynolds number.
图 4 随电磁力作用参数变化的圆柱尾迹Strouhal数
Fig. 4. The Strouhal number of the cylinder wake varying with the control number.
图 5 不同控制参数下随扰动波数变化的模态B增长率 (a)迎流面控制; (b)背流面控制; (c)全圆柱控制
Fig. 5. The growth rates of Mode B varying with the spanwise wavenumber for different control numbers: (a) Windward control; (b) leeward control; (c) global control.
图 6 不同控制参数下随扰动波数变化的模态A增长率 (a)迎流面控制; (b)背流面控制; (c)全圆柱控制
Fig. 6. The growth rates of Mode A varying with the spanwise wavenumber for different control numbers: (a) Windward control; (b) leeward control; (c) global control.
图 7 不同控制参数下最不稳定转捩模态的增长率 (a)模态A; (b)模态B
Fig. 7. The growth rate of the most unstable transition mode for different control numbers: (a) Mode A; (b) Mode B.
图 8 不同控制参数下的最不稳定转捩模态(云图为涡量) (a)无控制; (b)迎流面控制; (c)背流面控制; (d)全圆柱控制
Fig. 8. The unstable transition mode(the contour is the vorticity): (a) No control; (b) windward control; (c) leeward control; (d) global control.
图 9 无控制中椭圆不稳定和双曲不稳定诱导的时变无黏增长率 (a)椭圆不稳定诱导; (b)双曲不稳定诱导
Fig. 9. Variations of the inviscid growth rates induced by the elliptic instability and hyperbolic instability: (a) Induced by the elliptic instability; (b) induced by the hyperbolic instability.
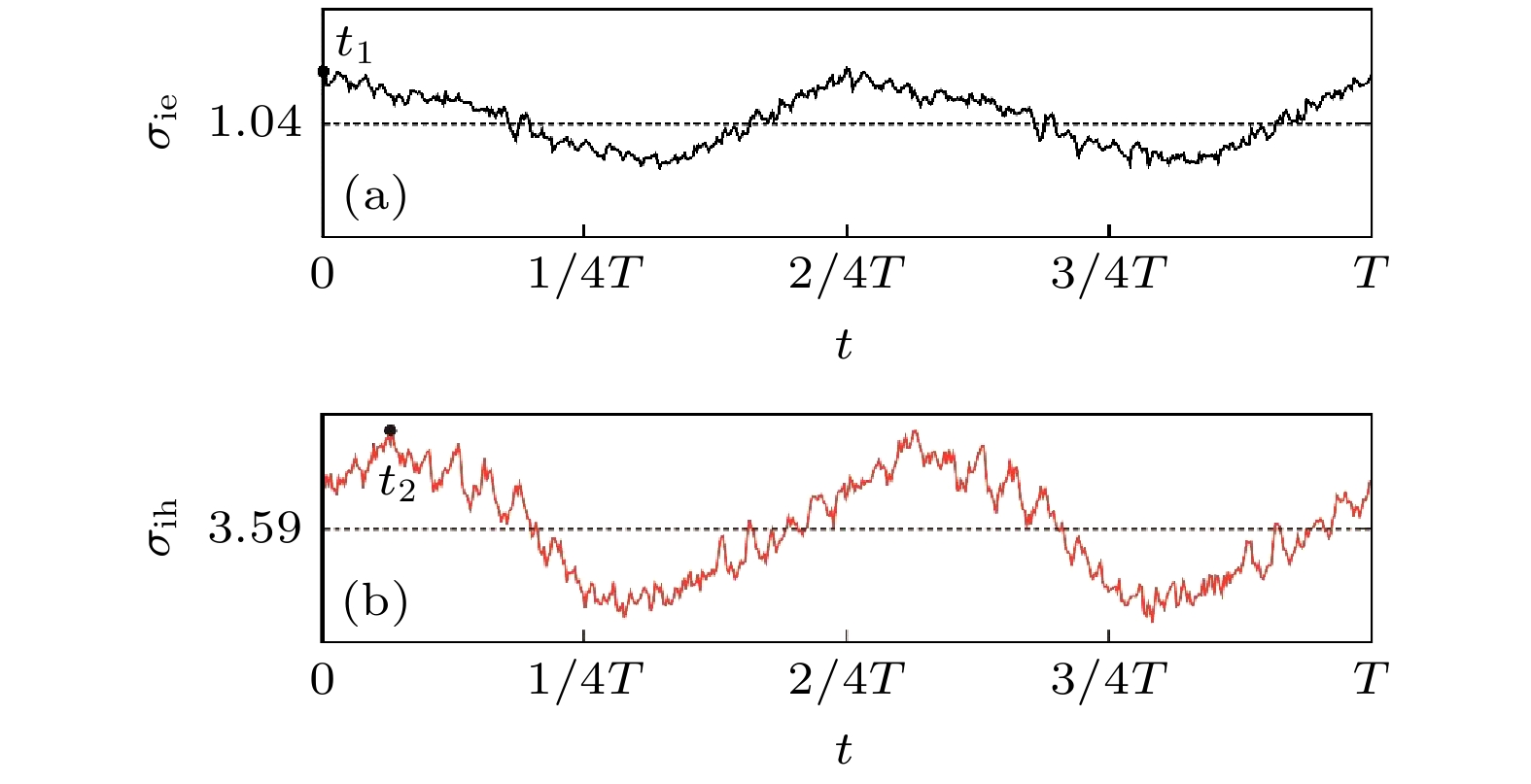
图 10 无控制中椭圆不稳定和双曲不稳定诱导的具有最大无黏增长率的区域(云图为无黏增长率) (a)
${t_1}$ 时刻椭圆不稳定诱导; (b)$ {t_2} $ 时刻双曲不稳定诱导Fig. 10. Regions with the maximum inviscid growth rates induced by the elliptic instability and hyperbolic instability: (a) Induced by the elliptic instability at
${t_1}$ ; (b) induced by the hyperbolic instability at${t_2}$ 
图 11 全圆柱控制中椭圆不稳定和双曲不稳定诱导的时变无黏增长率 (a)
$N = 0.6$ ; (b)$N = 0.8$ ; (c)$N = $ $ 1.0$ ; (d)$N = 1.2$ Fig. 11. Variations of the inviscid growth rates induced by the elliptic instability and hyperbolic instability with the time: (a)
$N = 0.6$ ; (b)$N = 0.8$ ; (c)$N = 1.0$ ; (d)$N = $ $ 1.2$ .
图 12 随电磁力作用参数变化的平均无黏增长率 (a)椭圆不稳定诱导; (b)双曲不稳定诱导
Fig. 12. Variations of the mean inviscid growth rates with the control numbers: (a) Induced by the elliptic instability; (b) induced by the hyperbolic instability
图 13 随时间变化的主Fourier模态能量
Fig. 13. The energy of the primary Fourier mode varying with the time.
图 14 不同控制工况下的圆柱三维尾迹结构
Fig. 14. The three-dimensional structures of the cylinder wake for different control cases.
图 15 模态B转捩形成的流场中流向不同位置展向速度脉动
Fig. 15. Distributions of the spanwise velocity pulsations along the wall-normalwise direction at different streamwise locations in the wake evolving from Mode B.
图 16 模态A转捩形成的流场中流向不同位置展向速度脉动
Fig. 16. Distributions of the spanwise velocity pulsations along the wall-normalwise direction at different streamwise locations in the wake evolving from Mode A.
表 1 不同插值阶数下的计算收敛性
Table 1. Convergence for different interpolation orders.
$\mathcal{K}$ ${\bar C_{\text{d}}}$ (%相对差值) ${\sigma _{\text{r}}}$ (%相对差值) 4 1.38497(–0.03) 0.14538( 0.12) 6 1.38463(–0.01) 0.14549( 0.04) 8 1.38440( 0.01) 0.14555( 0.00) 10 1.38450(—) 0.14555(—) 
下载: 导出CSV
表 2 不同控制参数下圆柱所受平均阻力
Table 2. The average drag for different control numbers.
无电磁力控制 迎流面控制 背流面控制 全圆柱控制 N = 0.6 N = 1.0 N = 0.6 N = 1.0 N = 0.6 N = 1.0 0.6591 0.6588 0.6594 0.6153 0.5590 0.6188 0.5642
下载: 导出CSV
-
[1] Williamson C H K 1996 Annu. Rev. Fluid. Mech. 28 477
Google Scholar
[2] Jackson C P 1987 J. Fluid Mech. 182 23
Google Scholar
[3] Barkley D, Henderson R D 1996 J. Fluid. Mech. 322 215
Google Scholar
[4] Jiang H Y, Cheng L 2020 Phys. Fluids 32 014103
Google Scholar
[5] McClure J, Pavan C, Yarusevych S 2019 Phys. Rev. Fluids 4 124702
Google Scholar
[6] Xu C, Mao Y J, Hu Z W 2019 Aerosp. Sci. Technol. 88 233
Google Scholar
[7] Gao D L, Huang Y W, Chen W L, Chen G B, Li H 2019 Phys. Fluids 31 057105
Google Scholar
[8] Del Guercio G, Cossu C, Pujals G 2014 J. Fluid Mech. 752 572
Google Scholar
[9] Xu F, Chen W L, Bai W F, Xiao Y Q, Qu J P 2017 Comput. Fluids 145 52
Google Scholar
[10] Mao X R, Sherwin S 2015 J. Fluid Mech. 775 241
Google Scholar
[11] 陈蒋力, 陈少强, 任峰, 胡海豹 2022 71 084701
Google Scholar
Chen J L, Chen S Q, Ren F, Hu H B 2022 Acta Phys. Sin. 71 084701
Google Scholar
[12] Li J C, Zhang M Q 2022 J. Fluid Mech. 932 A44
Google Scholar
[13] Marquet O, Sipp D, Jacquin L 2008 J. Fluid Mech. 615 221
Google Scholar
[14] Khodkar M A, Taira K 2020 J. Fluid Mech. 904 R1
Google Scholar
[15] Albrecht T, Stiller J, Metzkes H, Weier T, Gerbeth G 2013 Eur. Phys. J. Spec. Top. 220 275
Google Scholar
[16] Kim S, Lee C M 2001 Exp. Fluids 28 252
Google Scholar
[17] 尹纪富, 尤云祥, 李巍, 胡天群 2014 63 044701
Google Scholar
Yin J F, You Y X, Li W, Hu T Q 2014 Acta Phys. Sin. 63 044701
Google Scholar
[18] Zhang H, Fan B C, Chen Z H 2010 Eur. J. Mech. B-Fluids 29 53
Google Scholar
[19] Zhang H, Fan B C, Chen Z H, Li H Z 2014 J. Fluids Struct. 48 62
Google Scholar
[20] Zhang H, Liu M K, Han Y, Gui M Y, Li J, Chen Z H 2017 Comput. Fluids 159 112
Google Scholar
[21] 刘宗凯, 薄昱明, 王军, 崔珂 2017 66 084704
Google Scholar
Liu Z K, Bo Y M, Wang J, Cui K 2017 Acta Phys. Sin. 66 084704
Google Scholar
[22] Huang Y D, Zhou B M, Tang Z L 2017 Appl. Math. Mech. Engl. Ed. 38 439
Google Scholar
[23] Berger T W, Kim J, Lee C, Lim J 2000 Phys. Fluids 12 631
Google Scholar
[24] Du Y Q, Karniadakis G E 2000 Science 288 1230
Google Scholar
[25] Blackburn H M, Lee D, Albrecht T, Singh J 2019 Comput. Phys. Commun. 245 106804
Google Scholar
[26] Karniadakis G E, Israeli M, Orszag S A 1991 J. Comput. Phys. 97 414
Google Scholar
[27] Barkley D, Blackburn H M, Sherwin S J 2008 Int. J. Numer. Meth. Fluids 57 1435
Google Scholar
[28] Williamson C H K 1989 J Fluid Mech. 206 579
Google Scholar
[29] Hammache M, Gharib M 1991 J. Fluid Mech. 232 567
Google Scholar
[30] Thompsom M C, Leweke T, Williamson C H K 2001 J. Fluid Struct. 15 607
Google Scholar
[31] Jeong J, Hussain F 1995 J. Fluid Mech. 285 69
Google Scholar
下载:
计量
- 文章访问数: 3324
- PDF下载量: 54
- 被引次数: 0
