基于时程深度学习的复杂流场流动特性表征方法

战庆亮; 白春锦; 葛耀君

doi:10.7498/aps.71.20221314

摘要

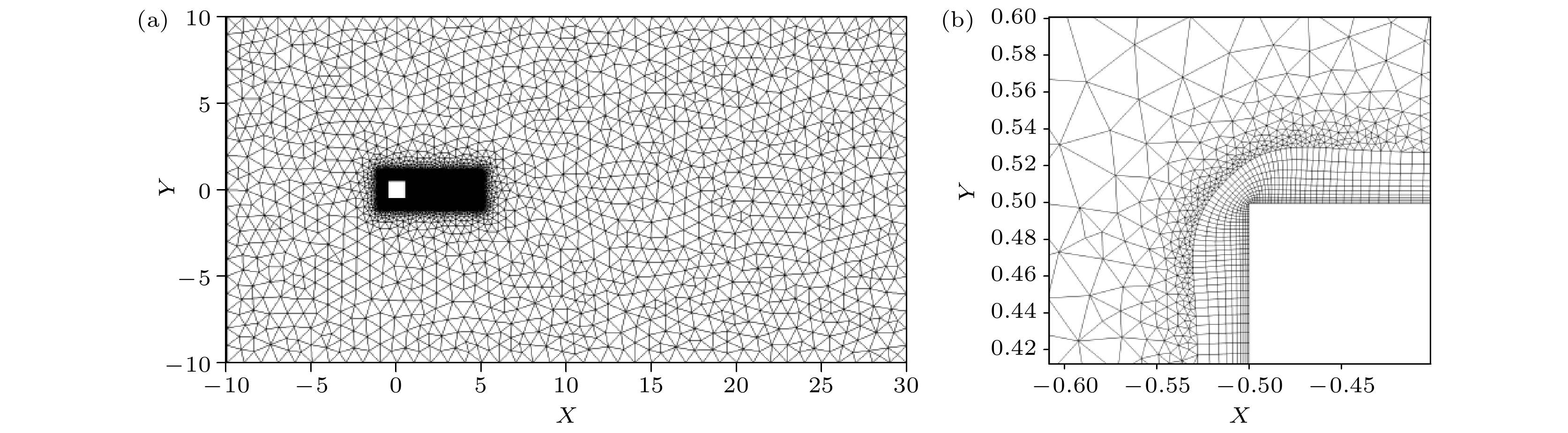
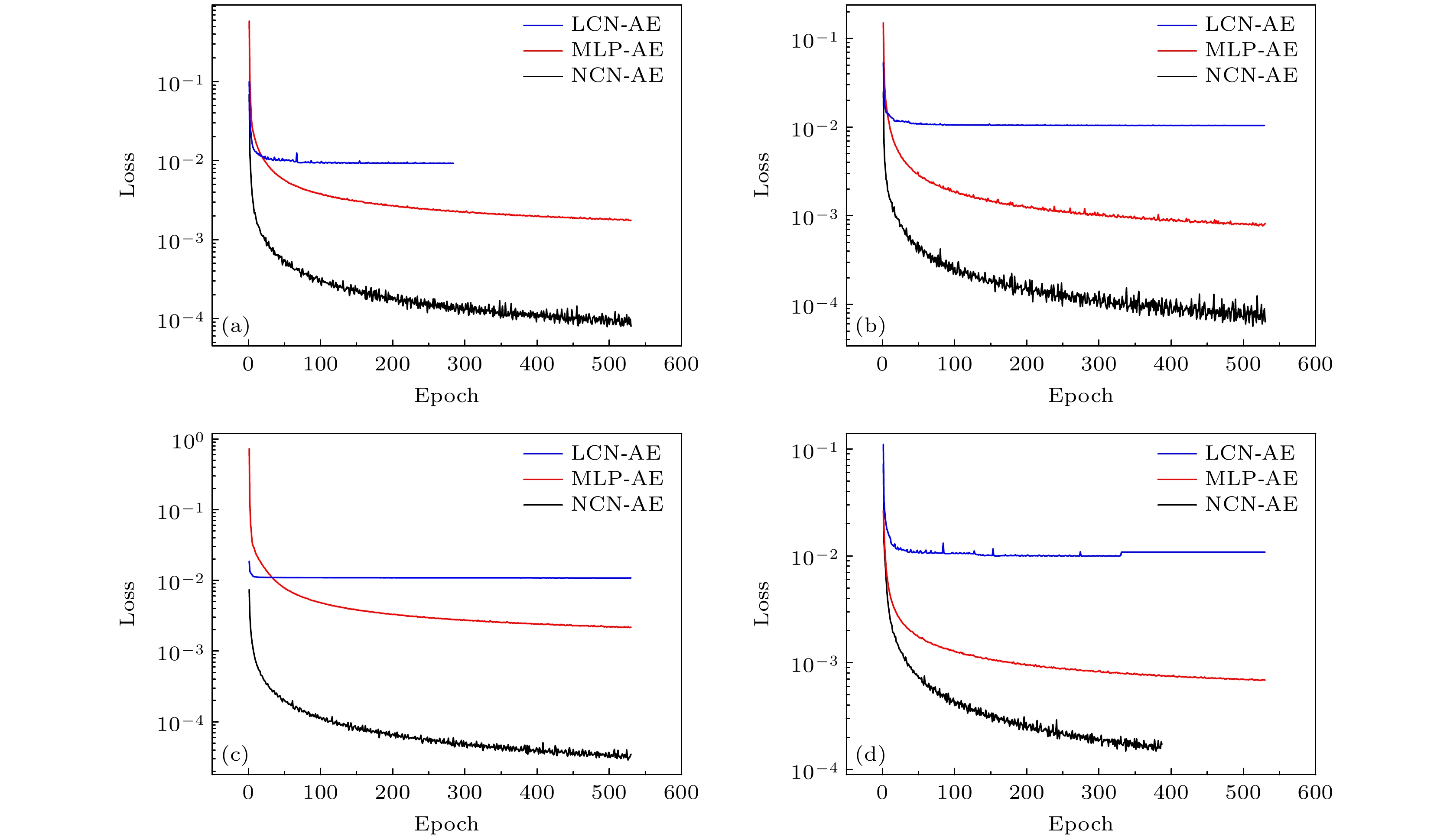
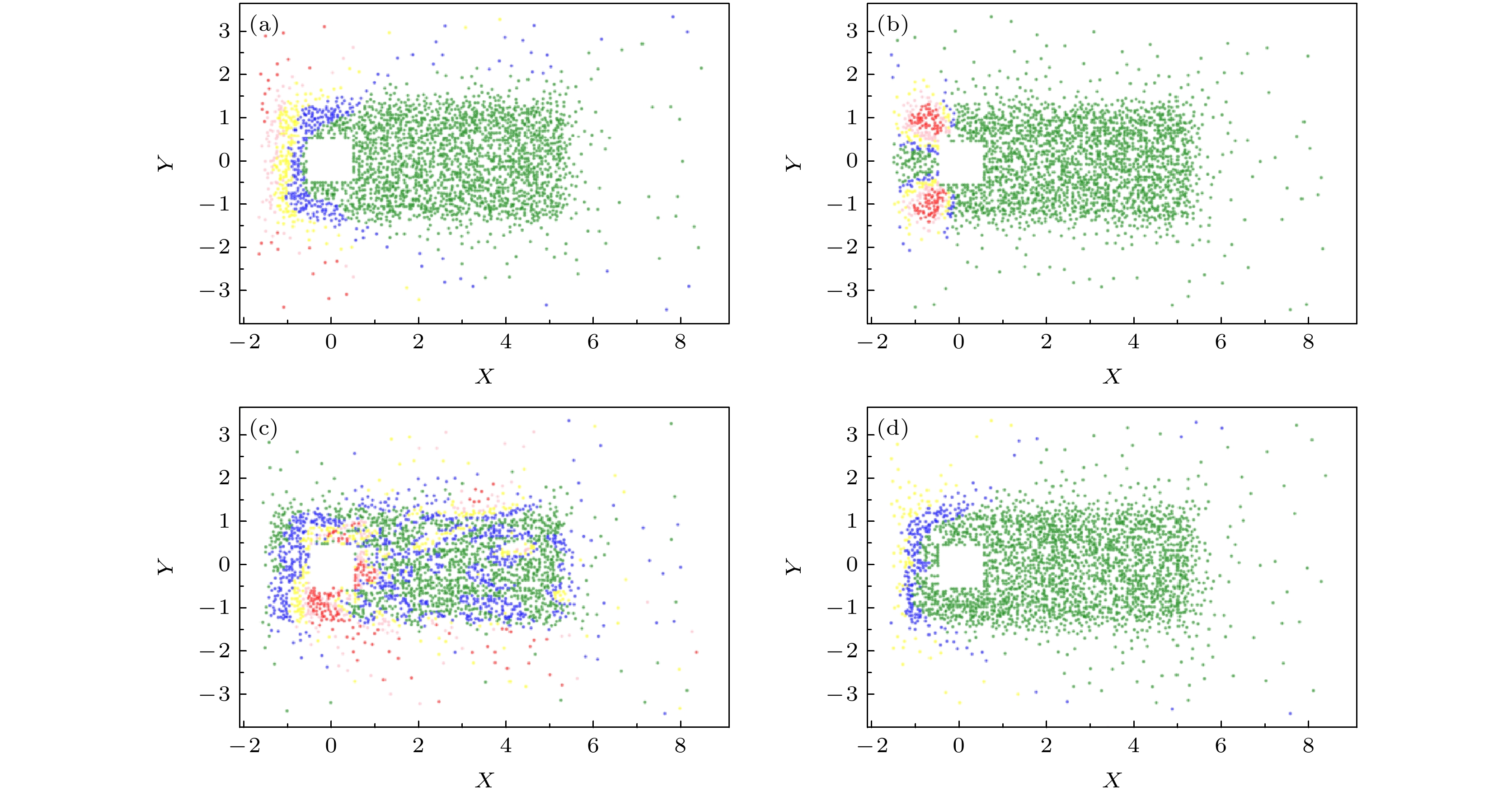
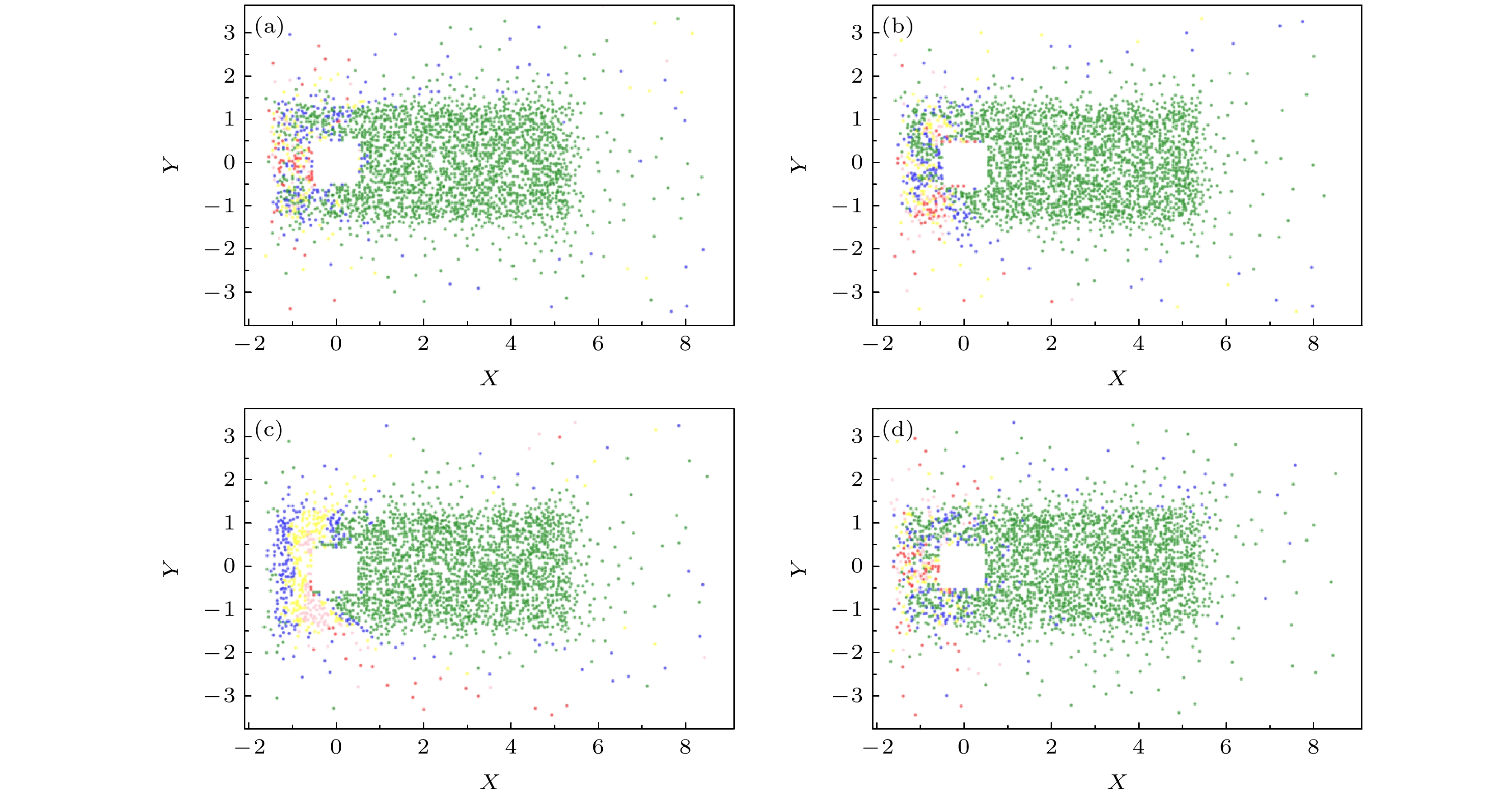
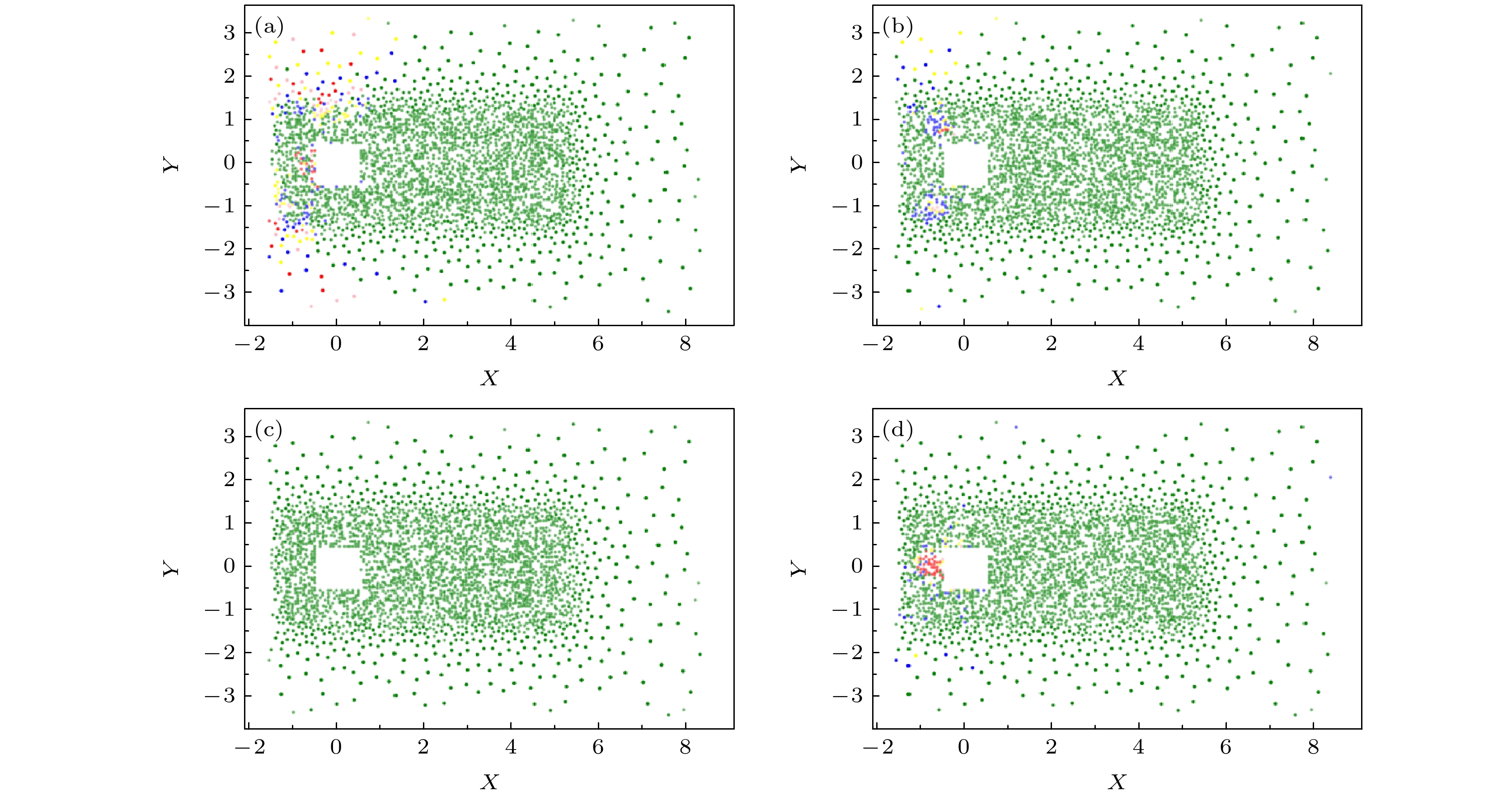
流场的特征分析与表征研究对流动机理的明确具有重要意义. 然而湍流流场具有复杂的非定常时空演化特征, 对其流场数据的低维表征有一定困难. 针对此问题, 本文提出了基于流场时程数据深度学习方法的湍流低维表征模型, 实现了复杂流动数据的降维表征. 分别建立了基于一维线性卷积、非线性全连接和非线性卷积的自动编码方法, 对非定常时程数据进行降维并得到了低维空间到时域的解码映射关系, 实现了特征提取与压缩. 通过Re = 2.2×10⁴的方柱绕流场进行了研究与验证, 结果表明: 时程深度学习方法可以有效地实现流场的低维表征, 适用于复杂湍流问题; 非线性一维卷积自编码器对复杂流场的表征准确性优于全连接和线性卷积方法. 本文方法是无监督训练方法, 可应用于基于一点的传感器数据处理中, 是研究复杂流场特征的新方法.

关键词:

Abstract

Flow analysis and low-dimensional representation model is of great significance in studying the complex flow mechanism. However, the turbulent flow field has complex and unstable spatiotemporal evolution feature, and it is difficult to establish the low-dimensional representation model for the flow big data. A low-dimensional representation model of complex flow is proposed and verified based on the flow time-history deep learning method. One-dimensional linear convolution, nonlinear full connection and nonlinear convolution autoencoding methods are established to reduce the dimension of unsteady flow time history data. The decoding mapping from low-dimensional space to time domain is obtained to build the representation model for turbulence. The proposed method is verified by using flow around the square clyinder with Re = 2.2×10⁴. The results show that the flow time-history deep learning method can be used to effectively realize the low-dimensional representation of the flow and is suitable for solving the complex turbulent flow problems; the nonlinear one-dimensional convolutional autoencoder is superior to the full connection and linear convolution methods in representing the complex flow features. The method in this work is an unsupervised training method, which can be widely used in single-point-based sensor data processing, and is a new method to study the characteristics of turbulence and complex flow problems.

Keywords:

作者及机构信息

1.
大连海事大学, 交通运输工程学院, 大连　116026

2.
同济大学, 土木工程防灾国家重点实验室, 上海　200092

通信作者: 战庆亮, zhanqingliang@163.com

基金项目: 国家自然科学基金(批准号: 51778495, 51978527)、桥梁结构抗风技术交通行业重点实验室(上海)开放课题(批准号: KLWRTBMC21-02)和中央高校基本科研业务费专项资金(批准号: 3132022189)资助的课题.

Authors and contacts

1.
College of Transportation and Engineering, Dalian Maritime University, Dalian 116026, China

2.
State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China

Corresponding author: Zhan Qing-Liang, zhanqingliang@163.com

Funds: Project supported by the the National Natural Science Foundation of China (Grant Nos. 51778495, 51978527), the Open Project of the Industry Key Laboratory of Bridge Structure Wind Resistance Technology (Shanghai), China (Grant No. KLWRTBMC21-02), and the Fundamental Research Funds for the Central Universities (Grant No. 3132022189).

文章全文 : translate this paragraph

参考文献

[1]	Berkooz G, Holmes P, Lumley J L 1993 Annu. Rev. Fluid Mech. 25 539 Google Scholar
[2]	Sirovich L 1987 Q. Appl. Math. 45 561 Google Scholar
[3]	Schmid P J, Sesterhenn J 2010 J. Fluid Mech. 656 5 Google Scholar
[4]	Clarence W R, Igor M, Shervin B, Philipp S, Dan S H 2009 J. Fluid Mech. 641 115 Google Scholar
[5]	金晓威, 赖马树金, 李惠 2021 力学学报 53 2616 Google Scholar Jin X W, Lai M S J, Li H 2021 Chin. J. Theor. Appl. Mech. 53 2616 Google Scholar
[6]	Ling J, Kurzawski A, Templeton J 2016 J. Fluid Mech. 807 155 Google Scholar
[7]	Li B, Yang Z, Zhang X, He G, Shen L 2020 J. Fluid Mech. 905 A10 Google Scholar
[8]	Raissi M, Karniadakis G E 2018 J. Comput. Phys. 357 125 Google Scholar
[9]	Kim H, Kim J, Won S, Lee C 2021 J. Fluid Mech. 910 A29 Google Scholar
[10]	Murata T, Fukami K, Fukagata K 2020 J. Fluid Mech. 882 A13 Google Scholar
[11]	Omata N, Shirayama S 2019 AIP Adv. 9 015006 Google Scholar
[12]	Fukami K, Fukagata K, Taira K 2021 J. Fluid Mech. 909 A9 Google Scholar
[13]	Liu B, Tang J, Huang H B, Lu X Y 2020 Phys. Fluids 32 025105 Google Scholar
[14]	Callaham J, Maeda K, Brunton S L 2019 Phys. Rev. Fluids 4 103907 Google Scholar
[15]	Fukami K, Maulik R, Ramachandra N, Fukagata K, Taira K 2021 Nat. Mach. Intell. 3 945 Google Scholar
[16]	Erichson N B, Mathelin L, Yao Z W, Brunton S L, Maboney M W, Kutz J N 2020 Proc. R. Soc. A: Math. Phys. Eng. Sci. 476 20200097 Google Scholar
[17]	Deng Z W, Chen Y J, Liu Y Z, Kim K C 2019 Phys. Fluids 31 075108 Google Scholar
[18]	Han R K, Wang Y X, Zhang Y, Chen C 2019 Phys. Fluids 31 127101 Google Scholar
[19]	Fukami K, Fukagata K, Taira K 2020 Theor. Comput. Fluid Dyn. 34 497 Google Scholar
[20]	战庆亮, 白春锦, 葛耀君 2022 力学学报 54 822 Google Scholar Zhan Q L, Bai C J, Ge Y J 2022 Chin. J. Theor. Appl. Mech. 54 822 Google Scholar
[21]	战庆亮, 白春锦, 张宁, 葛耀君 2022 航空学报 43 126531 Google Scholar Zhan Q L, Bai C J, Zhang N, Ge Y J 2022 Acta Aeronaut. Astronaut. Sin. 43 126531 Google Scholar
[22]	战庆亮, 葛耀君, 白春锦 2022 71 074701 Google Scholar Zhan Q L, Ge Y J, Bai C J 2022 Acta Phys. Sin. 71 074701 Google Scholar
[23]	战庆亮, 周志勇, 葛耀君 2015 哈尔滨工业大学学报 47 75 Google Scholar Zhan Q L, Zhou Z Y, Ge Y J 2015 J. Harbin Inst. Technol. 47 75 Google Scholar

施引文献

图 1 数据示意图

Fig. 1. Data type for modeling.

下载: 全尺寸图片幻灯片

图 2 整体计算域及平面网格划分　(a) 整体计算域; (b) 局部网格

Fig. 2. Global computational domain and plane grid settings: (a) Global computing domain; (b) local mesh.

下载: 全尺寸图片幻灯片

图 3 数值模拟结果　(a) 升力与阻力系数; (b) z = 0切面瞬时速度矢量图; (c) y = 0切面瞬时速度矢量图; (d) x = 2切面瞬时速度矢量图

Fig. 3. Partial results of simulation: (a) Lift and drag coefficient; (b) sectional instantaneous velocity vector diagram at z = 0; (c) sectional instantaneous velocity vector diagram at y = 0; (d) sectional instantaneous velocity vector diagram at x = 2.

下载: 全尺寸图片幻灯片

图 4 测点分布及时程结果　(a) 测点布置位置; (b) 部分测点的流向速度结果

Fig. 4. Distributions of monitoring points and time history results: (a) Layout position of measure points; (b) flow velocity of some measure points.

下载: 全尺寸图片幻灯片

图 5 表征模型的原理

Fig. 5. Methodology of the representation model.

下载: 全尺寸图片幻灯片

图 6 训练集的模型损失值　(a) 流向速度; (b) 横向速度; (c) 展向速度; (d) 速度绝对值

Fig. 6. Loss function of different models on training set: (a) Flow velocity; (b) lateral velocity; (c) spanwise velocity; (d) absolute value of velocity.

下载: 全尺寸图片幻灯片

图 7 线性卷积模型的误差分布　(a) 流向速度; (b) 横向速度; (c) 展向速度; (d) 速度绝对值

Fig. 7. Distributions of relatively error using LCN-AE: (a) Flow velocity; (b) lateral velocity; (c) spanwise velocity; (d) absolute value of velocity.

下载: 全尺寸图片幻灯片

图 8 全连接模型的误差分布　(a) 流向速度; (b) 横向速度; (c) 展向速度; (d) 速度绝对值

Fig. 8. Distribution of relatively error using MLP-AE: (a) Flow velocity; (b) lateral velocity; (c) spanwise velocity; (d) absolute value of velocity.

下载: 全尺寸图片幻灯片

图 9 非线性卷积模型的误差分布　(a) 流向速度; (b) 横向速度; (c) 展向速度; (d) 速度绝对值

Fig. 9. Distributions of relatively error using NCN-AE: (a) Flow velocity; (b) lateral velocity; (c) spanwise velocity; (d) absolute value of velocity.

下载: 全尺寸图片幻灯片

图 10 不同模型的误差散点图均值

Fig. 10. Mean relatively error of different models.

下载: 全尺寸图片幻灯片

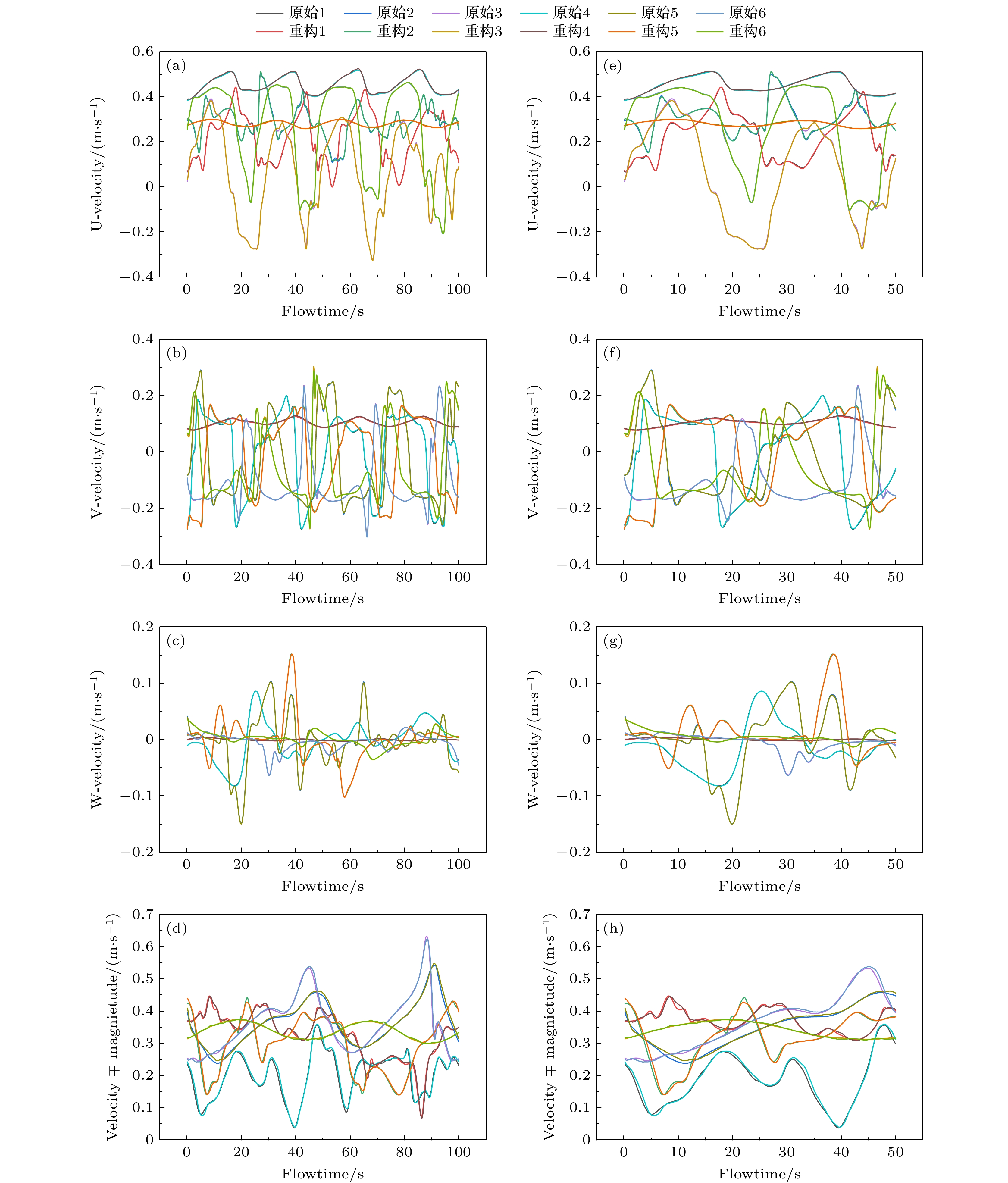
图 11 原始时程与重构时程的比较　(a) 流向速度; (b) 横向速度; (c) 展向速度; (d) 速度绝对值; (e) 流向速度的局部视图; (f) 横向速度的局部视图; (g) 展向速度的局部视图; (h) 速度绝对值的局部视图

Fig. 11. Comparision of original and reconstructed flow time history samples: (a) Flow velocity; (b) lateral velocity; (c) spanwise velocity; (d) absolute value of velocity; (e) partial view of flow velocity; (f) partial view of lateral velocity; (g) partial view of spanwise velocity; (h) partial view of absolute value of velocity.

下载: 全尺寸图片幻灯片

表 1 非线性卷积自动编码模型参数

Table 1. NCN-AE model parameters.

名称	滤波器个数	非线性激活方法
Input	—	—
Conv 1	64	ReLU
Conv 2	32	ReLU
Conv 3	20	ReLU
Flatten layer	—	—
Dense layer	20	ReLU
Code layer	20	ReLU
Dense layer2	20000
Reshape layer	—	—
Conv_T 1	20	ReLU
Conv_T 2	32	ReLU
Conv_T 3	64	ReLU
Output	1	ReLU

下载: 导出CSV

表 2 全连接自动编码模型参数

Table 2. MLP-AE model parameters.

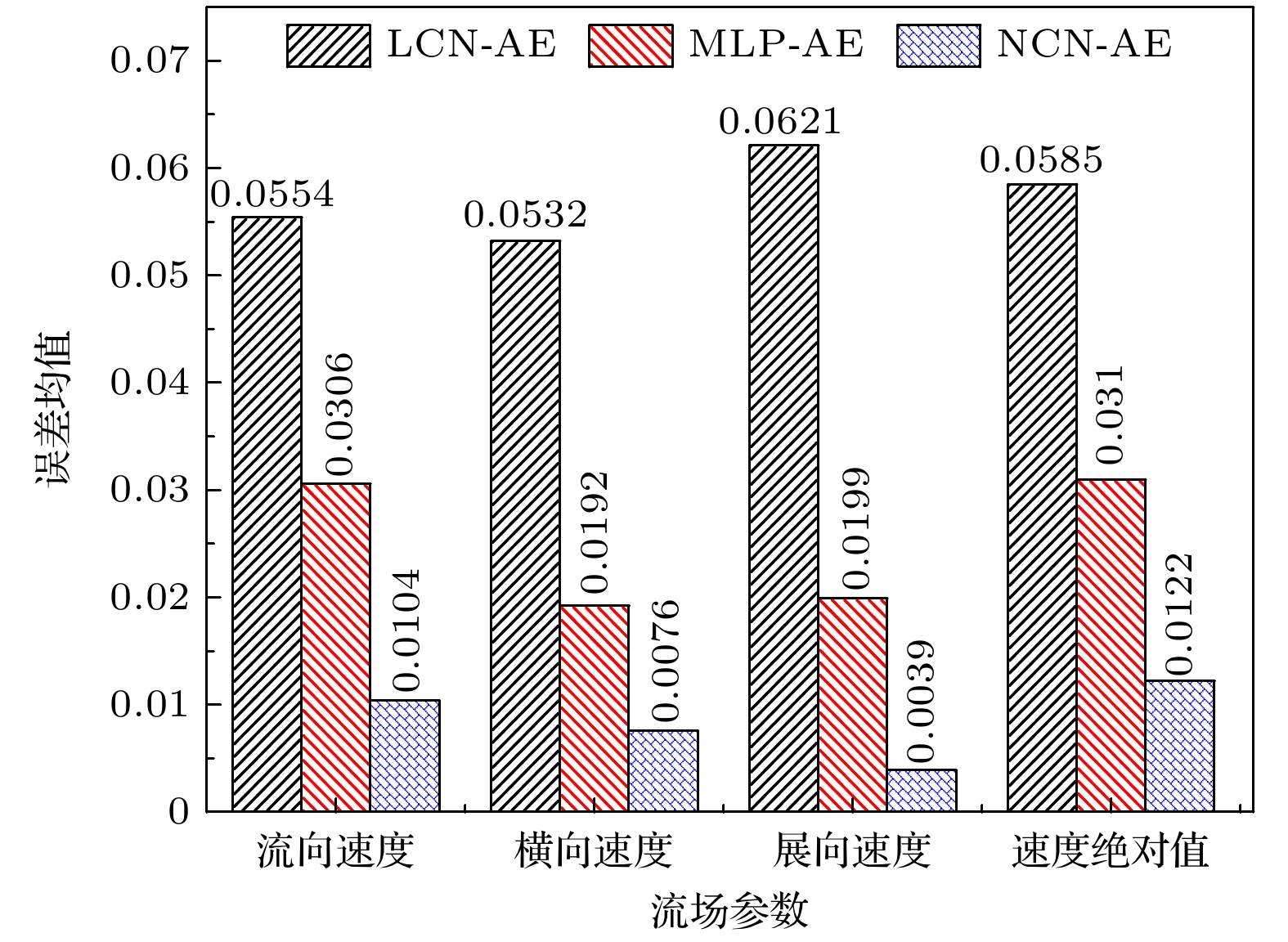
名称	神经元数	非线性激活方法
Input	—	—
Dense 1	64	ReLU
Dense 2	32	ReLU
Dense 3	20	ReLU
Flatten layer	—	—
Dense layer	20	ReLU
Code layer	20	ReLU
Dense layer2	20000
Reshape layer	—	—
Dense 1	20	ReLU
Dense 2	32	ReLU
Dense 3	64	ReLU
Output	1	ReLU

下载: 导出CSV

表 3 不同模型的误差散点图均值

Table 3. Mean relatively error of different models.

流场参数	LCN-AE	MLP-AE	NCN-AE
流向速度	0.0554	0.0306	0.0104
横向速度	0.0532	0.0192	0.0076
展向速度	0.0621	0.0199	0.0039
速度绝对值	0.0585	0.0310	0.0122

下载: 导出CSV

map

[1]	Berkooz G, Holmes P, Lumley J L 1993 Annu. Rev. Fluid Mech. 25 539 Google Scholar
[2]	Sirovich L 1987 Q. Appl. Math. 45 561 Google Scholar
[3]	Schmid P J, Sesterhenn J 2010 J. Fluid Mech. 656 5 Google Scholar
[4]	Clarence W R, Igor M, Shervin B, Philipp S, Dan S H 2009 J. Fluid Mech. 641 115 Google Scholar
[5]	金晓威, 赖马树金, 李惠 2021 力学学报 53 2616 Google Scholar Jin X W, Lai M S J, Li H 2021 Chin. J. Theor. Appl. Mech. 53 2616 Google Scholar
[6]	Ling J, Kurzawski A, Templeton J 2016 J. Fluid Mech. 807 155 Google Scholar
[7]	Li B, Yang Z, Zhang X, He G, Shen L 2020 J. Fluid Mech. 905 A10 Google Scholar
[8]	Raissi M, Karniadakis G E 2018 J. Comput. Phys. 357 125 Google Scholar
[9]	Kim H, Kim J, Won S, Lee C 2021 J. Fluid Mech. 910 A29 Google Scholar
[10]	Murata T, Fukami K, Fukagata K 2020 J. Fluid Mech. 882 A13 Google Scholar
[11]	Omata N, Shirayama S 2019 AIP Adv. 9 015006 Google Scholar
[12]	Fukami K, Fukagata K, Taira K 2021 J. Fluid Mech. 909 A9 Google Scholar
[13]	Liu B, Tang J, Huang H B, Lu X Y 2020 Phys. Fluids 32 025105 Google Scholar
[14]	Callaham J, Maeda K, Brunton S L 2019 Phys. Rev. Fluids 4 103907 Google Scholar
[15]	Fukami K, Maulik R, Ramachandra N, Fukagata K, Taira K 2021 Nat. Mach. Intell. 3 945 Google Scholar
[16]	Erichson N B, Mathelin L, Yao Z W, Brunton S L, Maboney M W, Kutz J N 2020 Proc. R. Soc. A: Math. Phys. Eng. Sci. 476 20200097 Google Scholar
[17]	Deng Z W, Chen Y J, Liu Y Z, Kim K C 2019 Phys. Fluids 31 075108 Google Scholar
[18]	Han R K, Wang Y X, Zhang Y, Chen C 2019 Phys. Fluids 31 127101 Google Scholar
[19]	Fukami K, Fukagata K, Taira K 2020 Theor. Comput. Fluid Dyn. 34 497 Google Scholar
[20]	战庆亮, 白春锦, 葛耀君 2022 力学学报 54 822 Google Scholar Zhan Q L, Bai C J, Ge Y J 2022 Chin. J. Theor. Appl. Mech. 54 822 Google Scholar
[21]	战庆亮, 白春锦, 张宁, 葛耀君 2022 航空学报 43 126531 Google Scholar Zhan Q L, Bai C J, Zhang N, Ge Y J 2022 Acta Aeronaut. Astronaut. Sin. 43 126531 Google Scholar
[22]	战庆亮, 葛耀君, 白春锦 2022 71 074701 Google Scholar Zhan Q L, Ge Y J, Bai C J 2022 Acta Phys. Sin. 71 074701 Google Scholar
[23]	战庆亮, 周志勇, 葛耀君 2015 哈尔滨工业大学学报 47 75 Google Scholar Zhan Q L, Zhou Z Y, Ge Y J 2015 J. Harbin Inst. Technol. 47 75 Google Scholar

[1]	施岳, 欧攀, 郑明, 邰含旭, 王玉红, 段若楠, 吴坚. 基于轻量残差复合增强收敛神经网络的粒子场计算层析成像伪影噪声抑制. , 2024, 73(10): 104202. doi: 10.7498/aps.73.20231902
[2]	欧阳鑫健, 张岩星, 王之龙, 张锋, 陈韦嘉, 庄园, 揭晓, 刘来君, 王大威. 面向铁电相变的机器学习: 基于图卷积神经网络的分子动力学模拟. , 2024, 73(8): 086301. doi: 10.7498/aps.73.20240156
[3]	罗仕超, 吴里银, 常雨. 高超声速湍流流动磁流体动力学控制机理. , 2022, 71(21): 214702. doi: 10.7498/aps.71.20220941
[4]	朱琦, 许多, 张元军, 李玉娟, 王文, 张海燕. 基于卷积神经网络的白蚀缺陷超声探测. , 2022, 71(24): 244301. doi: 10.7498/aps.71.20221504
[5]	张航, 胡月姣, 陈嘉文, 修龙汪. 程能映射下配光平移群的深度神经网络实现. , 2022, 71(13): 134201. doi: 10.7498/aps.71.20220178
[6]	战庆亮, 葛耀君, 白春锦. 基于深度学习的流场时程特征提取模型. , 2022, 71(7): 074701. doi: 10.7498/aps.71.20211373
[7]	隋怡晖, 郭星奕, 郁钧瑾, Alexander A. Solovev, 他得安, 许凯亮. 生成对抗网络加速超分辨率超声定位显微成像方法研究. , 2022, 71(22): 224301. doi: 10.7498/aps.71.20220954
[8]	赵伟瑞, 王浩, 张璐, 赵跃进, 褚春艳. 基于卷积神经网络的高精度分块镜共相检测方法. , 2022, 71(16): 164202. doi: 10.7498/aps.71.20220434
[9]	董帅, 纪祥勇, 李春曦. 横向磁场作用下Taylor-Couette湍流流动的大涡模拟. , 2021, 70(18): 184702. doi: 10.7498/aps.70.20210389
[10]	黄伟建, 李永涛, 黄远. 基于混合神经网络和注意力机制的混沌时间序列预测. , 2021, 70(1): 010501. doi: 10.7498/aps.70.20200899
[11]	周静, 张晓芳, 赵延庚. 一种基于图像融合和卷积神经网络的相位恢复方法. , 2021, 70(5): 054201. doi: 10.7498/aps.70.20201362
[12]	徐启伟, 王佩佩, 曾镇佳, 黄泽斌, 周新星, 刘俊敏, 李瑛, 陈书青, 范滇元. 基于深度卷积神经网络的大气湍流相位提取. , 2020, 69(1): 014209. doi: 10.7498/aps.69.20190982
[13]	王晨阳, 段倩倩, 周凯, 姚静, 苏敏, 傅意超, 纪俊羊, 洪鑫, 刘雪芹, 汪志勇. 基于遗传算法优化卷积长短记忆混合神经网络模型的光伏发电功率预测. , 2020, 69(10): 100701. doi: 10.7498/aps.69.20191935
[14]	彭向凯, 吉经纬, 李琳, 任伟, 项静峰, 刘亢亢, 程鹤楠, 张镇, 屈求智, 李唐, 刘亮, 吕德胜. 基于人工神经网络在线学习方法优化磁屏蔽特性参数. , 2019, 68(13): 130701. doi: 10.7498/aps.68.20190234
[15]	吴然超. 时滞离散神经网络的同步控制. , 2009, 58(1): 139-142. doi: 10.7498/aps.58.139
[16]	楼旭阳, 崔宝同. 混沌时滞神经网络系统的反同步. , 2008, 57(4): 2060-2067. doi: 10.7498/aps.57.2060
[17]	王占山, 张化光. 时滞递归神经网络中神经抑制的作用. , 2006, 55(11): 5674-5680. doi: 10.7498/aps.55.5674
[18]	崔万照, 朱长纯, 刘君华. 薄膜场发射开启电场的小波神经网络预测模型研究. , 2004, 53(5): 1583-1587. doi: 10.7498/aps.53.1583
[19]	. 神经网络的自适应删剪学习算法及其应用. , 2001, 50(4): 674-681. doi: 10.7498/aps.50.674
[20]	于丽娟, 朱长纯. 用人工神经网络预测场发射开启电场. , 2000, 49(1): 170-173. doi: 10.7498/aps.49.170

计量

文章访问数: 4182
PDF下载量: 85
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板