-
When the electromagnetic field in the sapphire resonator corresponds to the whispering gallery mode, it exhibits an extremely low dielectric loss. As result, sapphire oscillator has the characteristics of ultra-low phase noise and high short-term frequency stability. The distribution of electromagnetic field in the sapphire resonator is very important for realizing high-level oscillator. In this work, the radial-axial mode matching method is used to theoretically analyze the distribution of the field mode in the sapphire resonator, and the resonant frequency of the WGHm,0,0 mode is calculated. The field distribution of the sapphire resonator is simulated by the finite element analysis method. The gallery mode number of the sapphire resonator is studied and the electromagnetic field intensity distribution of the WGH15,0,0 mode in the azimuthal, axial and radial direction are obtained. Finally, a home-made gallery mode analyzer is used to measure the microwave field on the surface of sapphire resonator, which is composed of a three-dimensional rotating stage , the magnetic ring/probe coupling and a vector network analyzer. With the above theoretical analysis, the finite element analysis method and the experimental measurement, the working mode of the sapphire resonator and the resonant frequency of the WGHm,0,0 mode are determined. When the sapphire resonator works in WGH15,0,0 mode, the resonant frequency is 9.891 GHz, and the parameters of the whispering gallery mode in the resonator are obtained, and the unloaded Q value of the resonator is 94000. When the temperature is 292 K, the frequency-temperature sensitivity of the sapphire resonator working in the WGHm,0,0 whispering gallery mode is about
$71.64 \times 10^{-6}$ . The microwave oscillator consisting of the high Q sapphire resonator can be used to make an oscillator with ultra-low phase noise and high frequency stability.-
Keywords:
- sapphire resonator /
- whispering gallery mode /
- phase noise /
- quality factor
[1] Tobar M E, Krupka J, Ivanov E N, Woode R A 1997 J. Phys. D: Appl. Phys. 30 2770
Google Scholar
[2] Hartnett J G, Nand N R, Lu C 2012 Appl. Phys. Lett. 100 183501
Google Scholar
[3] Calosso C E, Vernotte F, Giordano V, Fluhr C, Dubois B, Rubiola E 2019 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 66 616
Google Scholar
[4] Santarelli G, Laurent Ph, Lemonde P, Clairon A, Mann A G, Chang S, Luiten A N, Salomon C 1999 Phys. Rev. Lett. 82 4619
Google Scholar
[5] Takamizawa A, Yanagimachi S, Hagimoto K 2022 Metrologia 59 035004
Google Scholar
[6] 王倩, 魏荣, 王育竹 2018 67 163202
Google Scholar
Wang Q, Wei R, Wang Y Z 2018 Acta Phys. Sin. 67 163202
Google Scholar
[7] Guena J, Abgrall M, Clairon A, Bize S 2014 Metro. 51 108
Google Scholar
[8] Thomson C A, McAllister B T, Goryachev M, Goryachev M, Ivanov E N, Tobar M E 2021 Phys. Rev. Lett. 126 081803
Google Scholar
[9] Campbell W M, McAllister B T, Goryachev M, Ivanov E N, Tobar M E 2021 Phys. Rev. Lett. 126 071301
Google Scholar
[10] Ball H, Oliver W D, Biercuk M J 2016 npj Quantum Inf. 2 1
Google Scholar
[11] Sepiol M A, Hughes A C, Tarlton J E, Nadlinger D P, Balance T G, Balance C J, Harty T P, Steane A M, Goodwin J F, Lucas D M 2019 Phys. Rev. Lett. 123 110503
Google Scholar
[12] Nand N R, Hartnett J G, Ivanov E N, Santarelli G 2011 IEEE Trans. Microwave Theory Tech. 59 2978
Google Scholar
[13] Doeleman S, Mai T, Rogers A E E, Hartnett J G, Tobar M E, Nand N 2011 PASP 123 582
Google Scholar
[14] Giordano V, Grop S, Dubois B, Bourgeois P Y, Kersalé Y, Haye G, Dolgovskiy V, Bucalovic N, Domenico G D, Schilt S, Chauvin J, Valat D, Rubiola E 2012 Rev. Sci. Instrum. 83 085113
Google Scholar
[15] Grop S, Giordano V, Bourgeois P Y, Bazin N, Kersale Y, Oxborrow M, Marra G, Langham C, Rubiola E, DeVincente J 2009 IEEE International Frequency Control Symp. Joint with the 22 nd European Frequency and Time Forum 376
Google Scholar
[16] Le Floch J M, Fan Y, Humbert G, Shan Q X, Férachou D, Bara-Maillet R, Aubourg M, Hartnett J G, Madrangeas V, Cros D, Blondy J M, Krupka, Tobar M E 2014 Rev. Sci. Instrum. 85 031301
Google Scholar
[17] Le Floch J M, Murphy C, Hartnett J G, Madrangeas V, Krupka J, Cros D, Tobar M E 2017 J. Appl. Phys. 121 014102
Google Scholar
[18] Krupka J, Derzakowski K, Abramowicz A, Tobar M E 1999 IEEE Trans. Microwave Theory Tech. 47 752
Google Scholar
[19] Tobar M E, Mann A G 1991 IEEE Trans. Microwave Theory Tech. 39 2077
Google Scholar
[20] Di Monaco O 1997 Ph. D. Dissertation (Besançon: Université de Franche Comté)
[21] Liang X P, Zaki K A 1993 IEEE Trans. Microwave Theory Tech. 41 2174
Google Scholar
[22] Rayleigh L 1910 The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 20 1001
Google Scholar
[23] Kobayashi Y, Tanaka S 1980 IEEE Trans. Microwave Theory Tech. 28 1077
Google Scholar
[24] Zaki K A, Atia A E 1983 IEEE Trans. Microwave Theory Tech. 31 1039
Google Scholar
[25] Peng H, Blair D G 1994 Proceedings of IEEE 48th Annual Symposium on Frequency Control 459
[26] Aubourg M, Guillon P 1991 JEWA 5 371
Google Scholar
[27] Strang G, Fix G J, Griffin D S 1974 J. Appl. Mech. 41 62
Google Scholar
[28] Jin J M 2002 The Finite Element Method in Electromagnetics (2nd Ed. ) (NewYork: Wiley-IEEE Press)
[29] Tobar M E, Krupka J, Ivanov E N, Woode R A 1996 IEEE International Frequency Control Symp. 799
[30] Shelby R, Fontanella J, Andeen C 1980 J. Phys. Chem. Solids 41 69
Google Scholar
[31] White G K 1993 Thermochim. Acta 218 83
Google Scholar
-
图 1 WGH15,0,0模式仿真 (a) 有限元模型网格填充剖面图; (b)电场方位角向分布; (c) 磁场径向分布
Fig. 1. WGH15,0,0: (a) Mesh filling section of finite element model; (b) azimuth distribution of electric field; (c) radial distribution of the magnetic field.
图 2 测量WGH模式共振频率装置示意图
Fig. 2. Schematic diagram of measuring WGH mode resonance frequency device.
图 3 WGH15,0,0模式电磁场强度 (a) 磁场强度方位角向分布; (b) 磁场强度轴向分布; (c)电场强度径向分布
Fig. 3. Electromagnetic field intensity of WGH15,0,0: (a) Cross-section distribution of magnetic field intensity; (b) axial cross-section distribution of magnetic field intensity; (c) cross-section distribution of electric field intensity diameter.
图 4 WGHm, 0, 0模式理论频率和测量频率的比较
Fig. 4. Comparison of theoretical and measured frequencies of WGHm, 0, 0 models.
图 5 室温下WGH15,0,0模式磁环不同位置的S21参数
Fig. 5. S21 at different positions of WGH15,0,0 mode magnetic rings in samples at room temperature.
图 6 室温下样品的WGH15,0,0模式S参数
Fig. 6. WGH15,0,0 mode S parameters of samples at room temperature.
图 7 WGH15,0,0谐振频率与样品尺寸关系 (a) 谐振频率与直径变化的关系; (b) 谐振频率与高度变化的关系
Fig. 7. Relationship between resonant frequency and sample size: (a) Relation between resonant frequency and diameter change; (b) relation between resonant frequency and height variation.
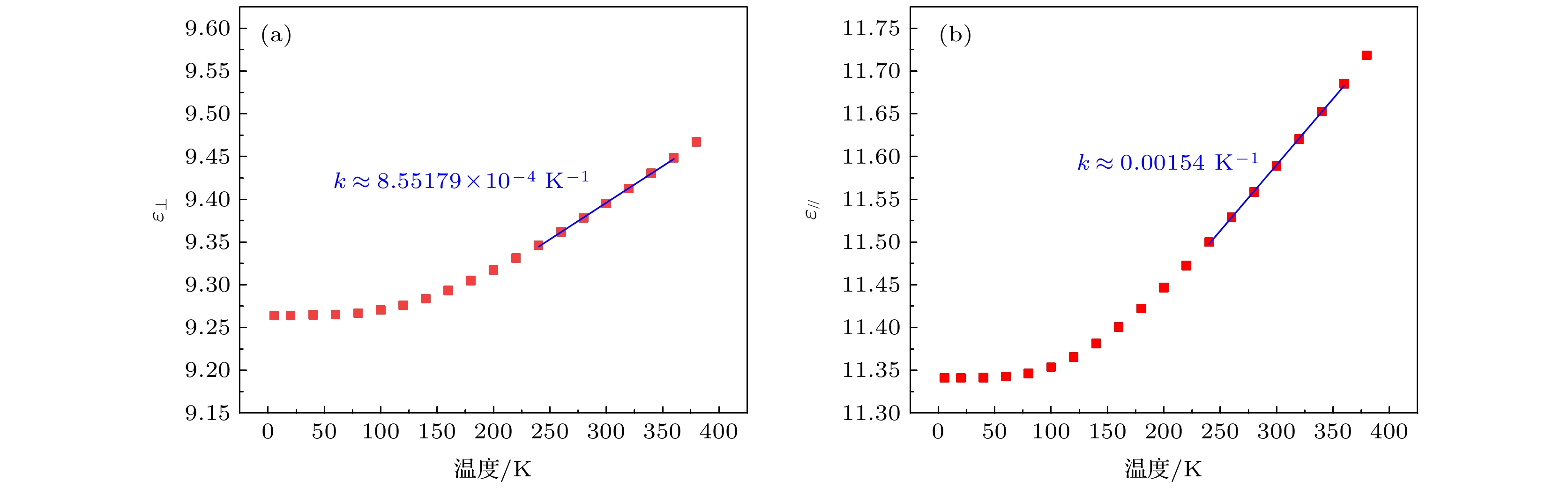
图 8 WGH15,0,0谐振频率与相对介电常数的关系 (a) 谐振频率与
${\varepsilon }_{\perp } $ 的关系; (b) 谐振频率与${\varepsilon }_{// }$ 的关系Fig. 8. Relation between resonant frequency and relative permittivity: (a) Relation between resonant frequency and
$ {\varepsilon }_{\perp } $ ; (b) relation between resonant frequency and${\varepsilon }_{//}$ .
图 9 温度对相对介电常数的影响 (a)
$ {\varepsilon }_{\perp } $ 与温度的关系; (b)${\varepsilon }_{// }$ 与温度的关系Fig. 9. Influence of temperature and relative permittivity: (a) Relationship between
${\varepsilon }_{\perp } $ and temperature; (b) relationship between${\varepsilon }_{// }$ and temperature.
图 10 温度对热膨胀系数的影响 (a)
$ {\alpha }_{D} $ 与温度的关系; (b)$ {\alpha }_{L} $ 与温度的关系Fig. 10. Influence of temperature and thermal coefficient of expansion: (a) Relationship between
$ {\alpha }_{D} $ and temperature; (b) relationship between$ {\alpha }_{L} $ and temperature.表 1 m = 10—19的谐振频率
Table 1. Resonant frequency of m = 10–19.
回音壁模式 f/GHz ${\Delta f}_{\rm{有}\rm{限}\rm{元}\text-\rm{理}\rm{论} }/{f}_{\rm{理}\rm{论} }$ ${\Delta f}_{\rm{测}\rm{量}\text-\rm{理}\rm{论} }/{f}_{\rm{理}\rm{论} }$ 理论计算 有限元法 实验测量 WGH10, 0,0 7.06686 7.07063 7.07181 0.053% 0.070% WGH11,0,0 7.63521 7.63784 7.63925 0.035% 0.053% WGH12,0,0 8.20160 8.20355 8.20443 0.024% 0.035% WGH13,0,0 8.76613 8.76745 8.76761 0.015% 0.017% WGH14,0,0 9.32905 9.33030 9.32983 0.013% 0.008% WGH15,0,0 9.89051 9.89011 9.89062 –0.004% 0.001% WGH16,0,0 10.45054 10.45390 10.45008 0.032% –0.004% WGH17,0,0 11.00933 11.01550 11.00863 0.056% –0.006% WGH18,0,0 11.56694 11.56940 11.56593 0.022% –0.009% WGH19,0,0 12.12345 12.12100 12.12218 –0.020% –0.010% 
下载: 导出CSV
-
[1] Tobar M E, Krupka J, Ivanov E N, Woode R A 1997 J. Phys. D: Appl. Phys. 30 2770
Google Scholar
[2] Hartnett J G, Nand N R, Lu C 2012 Appl. Phys. Lett. 100 183501
Google Scholar
[3] Calosso C E, Vernotte F, Giordano V, Fluhr C, Dubois B, Rubiola E 2019 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 66 616
Google Scholar
[4] Santarelli G, Laurent Ph, Lemonde P, Clairon A, Mann A G, Chang S, Luiten A N, Salomon C 1999 Phys. Rev. Lett. 82 4619
Google Scholar
[5] Takamizawa A, Yanagimachi S, Hagimoto K 2022 Metrologia 59 035004
Google Scholar
[6] 王倩, 魏荣, 王育竹 2018 67 163202
Google Scholar
Wang Q, Wei R, Wang Y Z 2018 Acta Phys. Sin. 67 163202
Google Scholar
[7] Guena J, Abgrall M, Clairon A, Bize S 2014 Metro. 51 108
Google Scholar
[8] Thomson C A, McAllister B T, Goryachev M, Goryachev M, Ivanov E N, Tobar M E 2021 Phys. Rev. Lett. 126 081803
Google Scholar
[9] Campbell W M, McAllister B T, Goryachev M, Ivanov E N, Tobar M E 2021 Phys. Rev. Lett. 126 071301
Google Scholar
[10] Ball H, Oliver W D, Biercuk M J 2016 npj Quantum Inf. 2 1
Google Scholar
[11] Sepiol M A, Hughes A C, Tarlton J E, Nadlinger D P, Balance T G, Balance C J, Harty T P, Steane A M, Goodwin J F, Lucas D M 2019 Phys. Rev. Lett. 123 110503
Google Scholar
[12] Nand N R, Hartnett J G, Ivanov E N, Santarelli G 2011 IEEE Trans. Microwave Theory Tech. 59 2978
Google Scholar
[13] Doeleman S, Mai T, Rogers A E E, Hartnett J G, Tobar M E, Nand N 2011 PASP 123 582
Google Scholar
[14] Giordano V, Grop S, Dubois B, Bourgeois P Y, Kersalé Y, Haye G, Dolgovskiy V, Bucalovic N, Domenico G D, Schilt S, Chauvin J, Valat D, Rubiola E 2012 Rev. Sci. Instrum. 83 085113
Google Scholar
[15] Grop S, Giordano V, Bourgeois P Y, Bazin N, Kersale Y, Oxborrow M, Marra G, Langham C, Rubiola E, DeVincente J 2009 IEEE International Frequency Control Symp. Joint with the 22 nd European Frequency and Time Forum 376
Google Scholar
[16] Le Floch J M, Fan Y, Humbert G, Shan Q X, Férachou D, Bara-Maillet R, Aubourg M, Hartnett J G, Madrangeas V, Cros D, Blondy J M, Krupka, Tobar M E 2014 Rev. Sci. Instrum. 85 031301
Google Scholar
[17] Le Floch J M, Murphy C, Hartnett J G, Madrangeas V, Krupka J, Cros D, Tobar M E 2017 J. Appl. Phys. 121 014102
Google Scholar
[18] Krupka J, Derzakowski K, Abramowicz A, Tobar M E 1999 IEEE Trans. Microwave Theory Tech. 47 752
Google Scholar
[19] Tobar M E, Mann A G 1991 IEEE Trans. Microwave Theory Tech. 39 2077
Google Scholar
[20] Di Monaco O 1997 Ph. D. Dissertation (Besançon: Université de Franche Comté)
[21] Liang X P, Zaki K A 1993 IEEE Trans. Microwave Theory Tech. 41 2174
Google Scholar
[22] Rayleigh L 1910 The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 20 1001
Google Scholar
[23] Kobayashi Y, Tanaka S 1980 IEEE Trans. Microwave Theory Tech. 28 1077
Google Scholar
[24] Zaki K A, Atia A E 1983 IEEE Trans. Microwave Theory Tech. 31 1039
Google Scholar
[25] Peng H, Blair D G 1994 Proceedings of IEEE 48th Annual Symposium on Frequency Control 459
[26] Aubourg M, Guillon P 1991 JEWA 5 371
Google Scholar
[27] Strang G, Fix G J, Griffin D S 1974 J. Appl. Mech. 41 62
Google Scholar
[28] Jin J M 2002 The Finite Element Method in Electromagnetics (2nd Ed. ) (NewYork: Wiley-IEEE Press)
[29] Tobar M E, Krupka J, Ivanov E N, Woode R A 1996 IEEE International Frequency Control Symp. 799
[30] Shelby R, Fontanella J, Andeen C 1980 J. Phys. Chem. Solids 41 69
Google Scholar
[31] White G K 1993 Thermochim. Acta 218 83
Google Scholar
下载:
计量
- 文章访问数: 3831
- PDF下载量: 48
- 被引次数: 0
