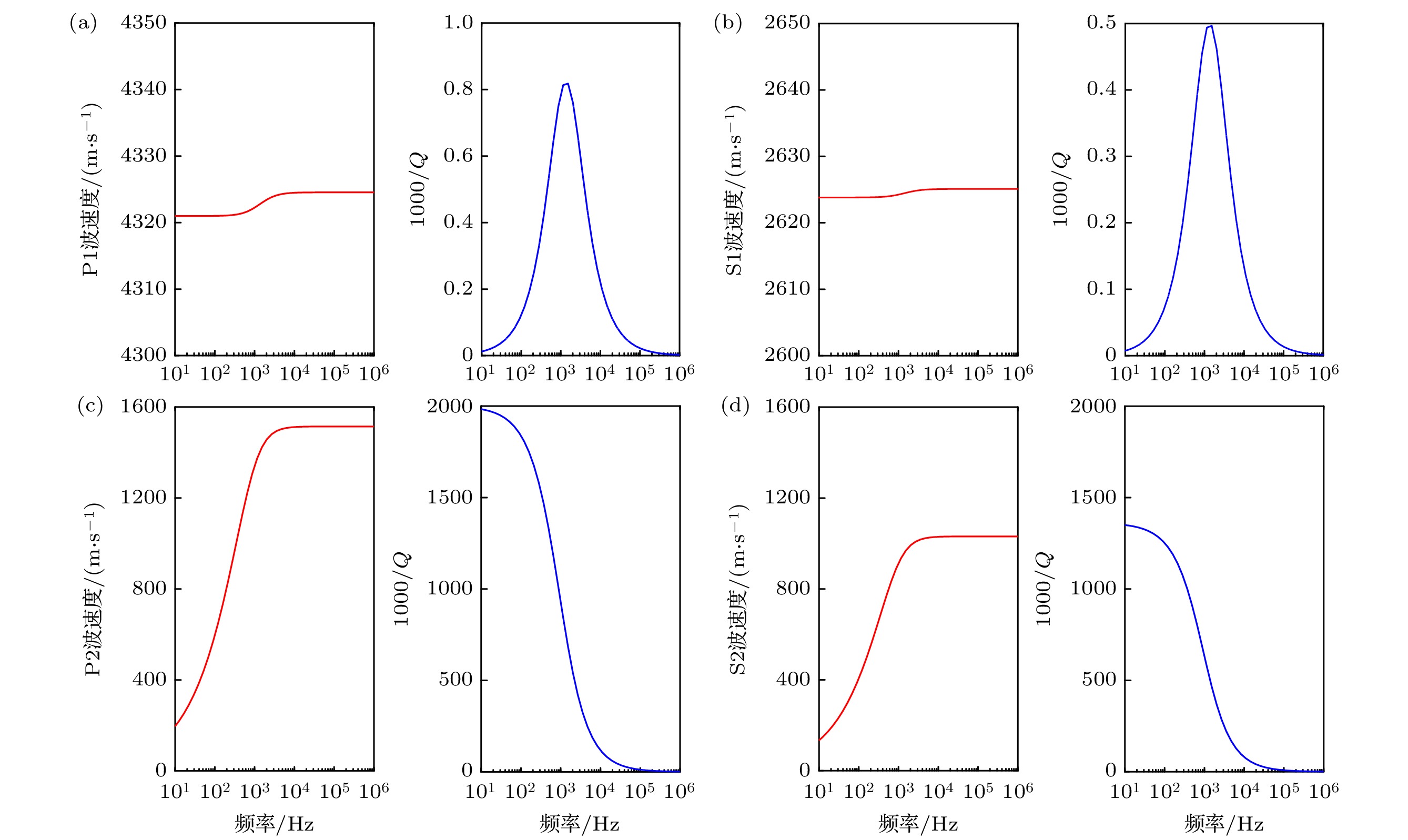
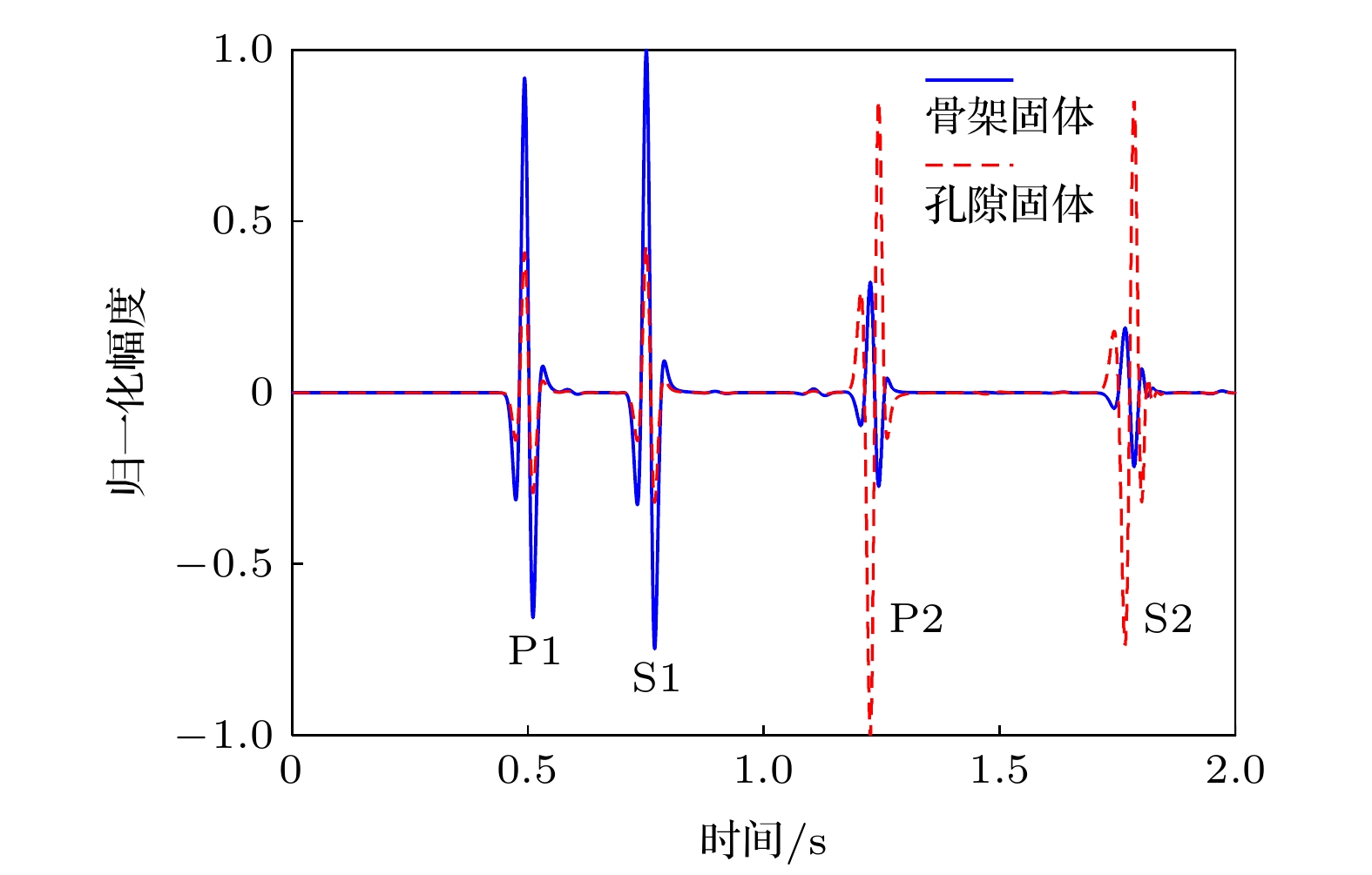
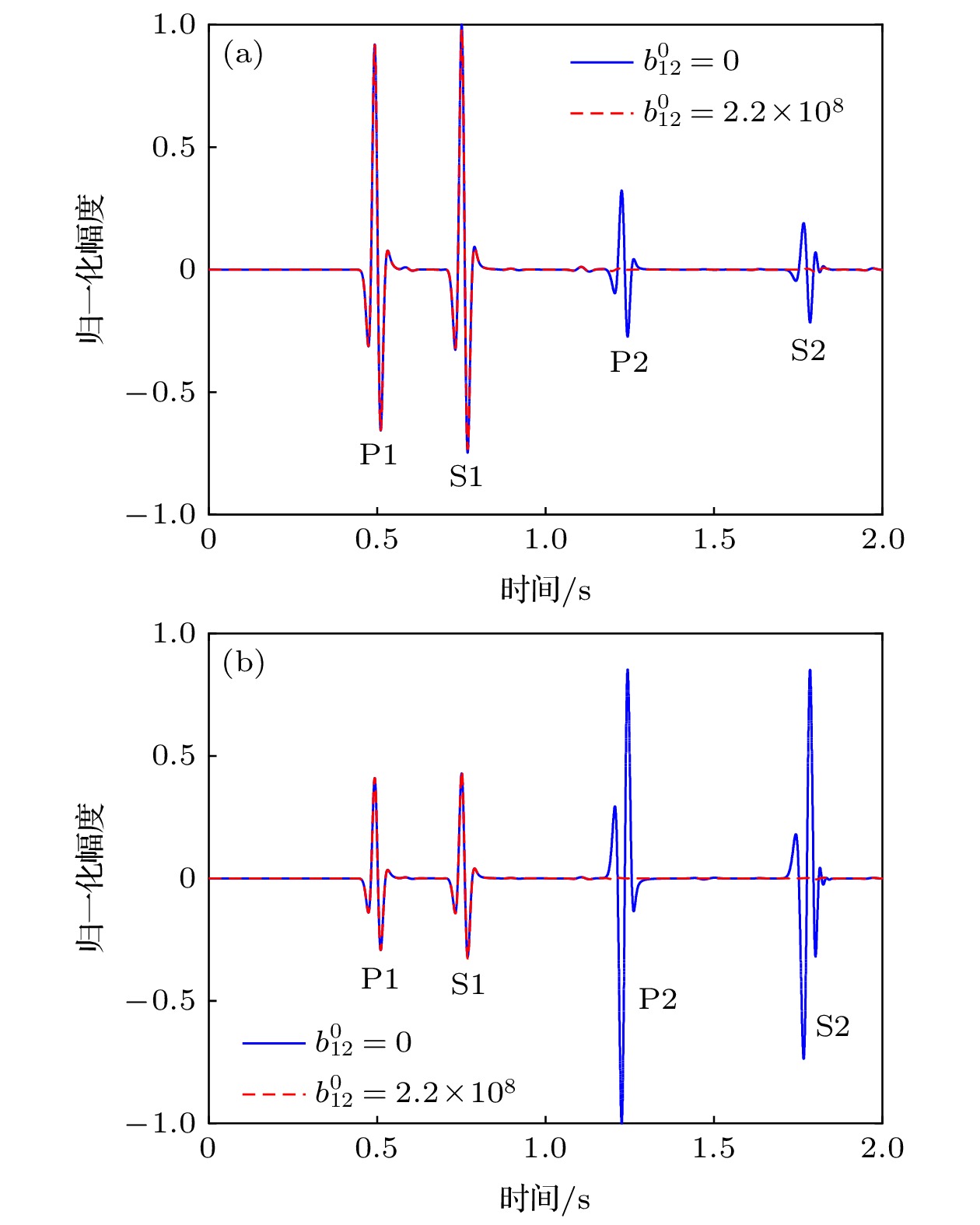
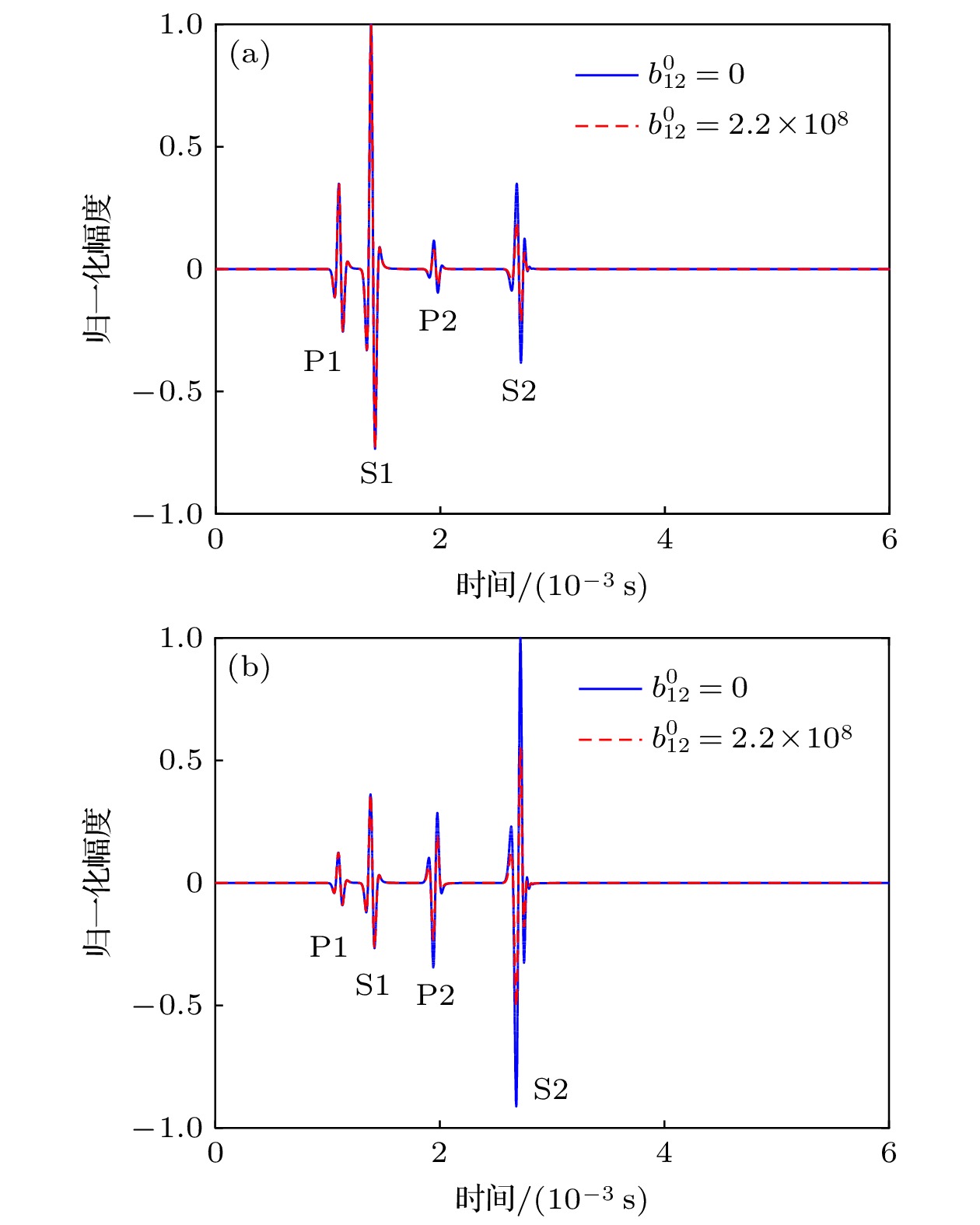
-
连通孔隙空间被有别于骨架固体的另一种固相介质充填而形成的双组分连通固体孔隙介质, 简称固-固孔隙介质. 推导出了固-固孔隙介质的声波动力学方程和本构关系, 利用平面波分析的方法研究了各种波的频散和衰减特性. 在此基础上, 提出了基于一阶速度-应力方程的时间分裂的高阶交错网格有限差分算法, 对其中的声场演化特点进行了模拟计算, 分析了各种波的产生机制和能量分布, 并详细讨论了两种固体间的摩擦系数和声源频率对各种波传播特性的影响. 数值模拟表明: 固-固孔隙介质中存在两种纵波(P1和P2)和两种横波(S1和S2), 其中P1和S1波能量主要在骨架固体中传播; P2和S2波是骨架固体和孔隙固体之间相对运动产生的慢波, 能量主要在孔隙固体中传播. 固体骨架和孔隙固体之间的摩擦主要影响慢波(P2和S2)的衰减, 且低频时衰减大于高频.
-
关键词:
- 孔隙介质声学 /
- 时间分裂的交错网格有限差分 /
- 平面波分析 /
- 传播特性
Aiming at the propagation characteristics of acoustic waves in a porous medium containing a solid in pores, the equations of motion and constitutive relation are deducted in the case of two-solid porous media. The frequency dispersion and attenuation characteristics of wave modes are analyzed by a plane wave analysis. In addition, based on the first-order velocity-stress equations, the time-splitting high-order staggered-grid finite-difference algorithm is proposed and constructed for understanding wave propagation mechanisms in such a medium, where the time-splitting method is used to solve the stiffness problem in the first-order velocity-stress equations. The generation mechanisms and energy distributions of different kinds of waves are investigated in detail. In particular, the influences of the friction coefficient between solid grains and pore solid as well as frequency on wave propagation are analyzed. It can be known from the results of plane wave analysis that there are two compression waves (P1 and P2) and two shear waves (S1 and S2) in a porous medium containing a solid in pores. The attenuations of P2 wave and S2 wave are much larger than those of P1 wave and S1 wave. This is due to the friction between the solid grains and the pore solid. The results show that our proposed numerical simulation algorithm can effectively solve the problem of stiffness in the velocity-stress equations, with high accuracy. The excitation mechanisms of the four wave modes are clearly revealed by the simulation results. The P1 wave and S1 wave propagate primarily in the solid grain frame, while P2 wave and S2 wave are concentrated mainly in the pore solid, which are caused by the relative motion between the solid grains and the pore solid. Besides, it should be pointed out that the wave diffusions of the P2 wave and S2 wave are influenced by the friction coefficient between solid grains and pore solid. The existence of friction coefficient between two solids makes P2 wave and S2 wave attenuate to a certain extent at high frequency, but the attenuation is much smaller than that at low frequency. This is the reason why it is difficult to observe the slow waves in practice. However, because the slow waves also carry some energy, it may not be ignored in the studying of the energy attenuation of acoustic waves in porous media.-
Keywords:
- porous media acoustics /
- time-splitting staggered-grid finite-difference /
- plan wave analysis /
- propagation characteristics
[1] Biot M A 1956 J. Acoust. Soc. Am. 28 168
Google Scholar
[2] Biot M A 1956 J. Acoust. Soc. Am. 28 179
Google Scholar
[3] Biot M A 1962 J. Appl. Phys. 33 1482
Google Scholar
[4] Biot M A 1962 J. Acoust. Soc. Am. 34 1254
Google Scholar
[5] Plona T J 1980 Appl. Phys. Lett. 36 259
Google Scholar
[6] 王秀明, 张海澜, 王东 2005 地球 46 1206
Google Scholar
Wang X M, Zhang H L, Wang D 2005 Chin. J. Geophys. 46 1206
Google Scholar
[7] 刘财, 杨庆节, 鹿琪, 郭智奇, 刘洋, 兰慧田, 耿美霞, 王典 2014 地球 57 2885
Google Scholar
Liu C, Yang Q J, Lu Q, Guo Z Q, Liu Y, Lan H T, Geng M X, Wang D 2014 Chin. J. Geophys. 57 2885
Google Scholar
[8] Ba J, Carcione J M, Nie J X 2011 J. Geophys. Res. 116 B06202
Google Scholar
[9] 崔志文, 刘金霞, 王春霞, 王克协 2010 59 8655
Google Scholar
Cui Z W, Liu J X, Wang C X, Wang K X 2010 Acta Phys. Sin. 59 8655
Google Scholar
[10] 丁卫, 吴文雯, 王驰, 吴智强 2014 63 224301
Google Scholar
Ding W, Wu W W, Wang C, Wu Z Q 2014 Acta Phys. Sin. 63 224301
Google Scholar
[11] Ba J, Carcione J M, Sun W 2015 Geophys. J. Int. 202 1843
Google Scholar
[12] Ba J, Xu W, Fu L Y, Carcione J M, Zhang L 2017 J. Geophys. Res-Sol. Ea. 122 1949
Google Scholar
[13] 王婷, 崔志文, 刘金霞, 王克协 2018 67 114301
Google Scholar
Wang T, Cui Z W, Liu J X, Wang K X 2018 Acta Phys. Sin. 67 114301
Google Scholar
[14] 周永潮, 许恒磊, 陈佳代, 张仪萍, 唐耀, 彭宇 2022 岩土工程学报 44 255
Google Scholar
Zhou Y C, Xu H L, Chen J D, Zhang Y P, Tang Y, Peng Y 2022 Chin. J. Geotech. Eng. 44 255
Google Scholar
[15] 李好婷, 朱玉颖, 孔德, 张旭瞳, 王淑彦 2021 工程热 42 2017
Li H T, Zhu Y Y, Kong D, Zhang X T, Wang S Y 2021 J. Engine. The. 42 2017
[16] 秦雷 2018 北京信息科技大学学报 33 1
Google Scholar
Qin L 2018 J. Beijing Inform. Sci. & Tech. Uni. 33 1
Google Scholar
[17] 仲超 2019 博士学位论文 (北京: 北京邮电大学)
Zhong C 2019 Ph. D Dissertation (Beijing: Beijing University of Posts and Telecommunications) (in Chinese)
[18] Zhu X, McMechan G A 1990 Geophysics 56 328
Google Scholar
[19] Dai N, Vafidis A, Kanasewich E R 1995 Geophysics 60 327
Google Scholar
[20] Carcione J M, Quiroga-Goode G 1996 Geophys. Pros. 44 99
Google Scholar
[21] Atalla N, Panneton R, Debergue P 1996 J. Acoust. Soc. Am. 104 1444
[22] Panneton R, Atalla N 1997 J. Acoust. Soc. Am. 101 3287
Google Scholar
[23] 杜启振, 刘莲莲, 孙晶波 2007 56 6143
Google Scholar
Du Q Z, Liu L L, Sun J B 2007 Acta Phys. Sin. 56 6143
Google Scholar
[24] Zhao H B, Wang X M, Chen H 2006 Chin. Phys. 15 2819
Google Scholar
[25] Santos J E, Corberó J M, Douglas J 1990 J. Acoust. Soc. Am. 87 1428
Google Scholar
[26] Carcione J M, Seriani G 2001 J. Comput. Phys. 170 6765
Google Scholar
[27] Gao J H, Zhang Y J 2013 Math. Probl. Eng. 5 707
Google Scholar
[28] Zhang Y, Gao J, Peng J 2018 IEEE Trans. Geosci. Remote Sens. 56 2991
Google Scholar
[29] Zhan Q, Zhuang M, Mao Y, Liu Q H 2020 J. Comput. Phys. 402 108961
Google Scholar
[30] Liu L, Zhang X M, Wang X M 2021 Chin. Phys. B. 30 024301
Google Scholar
[31] 兰慧田, 刘财, 郭智奇 2014 世界地质 33 190
Google Scholar
Lan H Y, Liu C, Guo Z Q 2014 Global Geol. 33 190
Google Scholar
[32] Leclaire P, Cohen-Ténoudji F, Aguirre-Puente J 1994 J. Acoust. Soc. Am. 96 3753
Google Scholar
[33] Berryman J G, Wang H F 2000 Int. J. Rock Mech. Min. 37 63
Google Scholar
[34] Guerin G, Goldberg D 2005 Geochem. Geophy. Geosy. 6 1
Google Scholar
[35] Carcione J M, Gurevich B, Cavallini F 2000 Geophys. Prospect. 48 539
Google Scholar
-
图 1 各场量在交错网格有限差分法中的位置分布
Fig. 1. Distribution of the field components in the staggered-grid finite-difference algorithm.
图 2 相速度和衰减随频率的变化曲线 (
$\phi $ = 0.3,$b_{12}^0 = 2.2 \times {10^8}$ ) (a) P1波; (b) S1波; (c) P2波; (d) S2波Fig. 2. Effects of frequency on the phase velocities and attenuation of waves (
$\phi $ = 0.3,$b_{12}^0 = 2.2 \times {10^8}$ ): (a) P1; (b) S1; (c) P2; (d) S2
图 3 频率为20 Hz且
${b_{12}} = 0$ 时, 0.45 s时刻质点振动速度水平及垂直分量波场快照 (a) 骨架固体质点振动速度水平分量; (b) 填充固体质点振动速度水平分量; (c) 骨架固体质点振动速度垂直分量; (d) 填充固体质点振动速度垂直分量Fig. 3. Snapshots of the (a), (b) horizontal and (c), (d) vertical particle velocity component of (a), (c) solid grain frame and (b), (d) pore solid when the frequency is 20 Hz and
${b_{12}} = 0$ at 0.45 s.
图 4 频率为20 Hz且
${b_{12}} = 0$ 时, 各相质点振动速度水平分量的波形Fig. 4. Waveform comparisons of the horizontal particle velocity component between different phases when the frequency is 20 Hz and
${b_{12}} = 0$ (normalized).
图 5 频率为20 Hz且
$b_{12}^0 = 2.2 \times {10^8}$ 时, 0.45 s时刻质点振动速度水平分量波场快照 (a) 骨架固体; (b) 填充固体Fig. 5. Snapshots of the horizontal particle velocity component when the frequency is 20 Hz and
$b_{12}^0 = 2.2 \times {10^8}$ at 0.45 s: (a) Solid grain frame; (b) pore solid.
图 6 频率为20 Hz且
$b_{12}^0 = 2.2 \times {10^8}$ 时, 各相质点振动速度水平分量的波形Fig. 6. Waveform comparisons of the horizontal particle velocity component between different phases when the frequency is 20 Hz and
$b_{12}^0 = 2.2 \times {10^8}$ (normalized).
图 7 频率为20 Hz时,
$b_{12}^0 = 0$ 和$b_{12}^0 = 2.2 \times {10^8}$ 两种情况下各相质点振动速度水平分量的波形 (a) 骨架固体; (b) 填充固体Fig. 7. Waveforms of the horizontal velocity component of each phase when
$b_{12}^0 = 0$ and$b_{12}^0 = 2.2 \times {10^8}$ (the frequency is 20 Hz): (a) Solid grain frame; (b) pore solid.
图 8 频率为10 kHz时,
$b_{12}^0 = 0$ 和$b_{12}^0 = 2.2 \times {10^8}$ 两种情况下各相质点振动速度水平分量的波形 (a) 骨架固体; (b) 孔隙固体Fig. 8. Waveforms of the horizontal velocity component of each phase when
$b_{12}^0 = 0$ and$b_{12}^0 = 2.2 \times {10^8}$ (the frequency is 10 kHz): (a) Solid grain frame; (b) pore solid.表 1 模型物性参数表
Table 1. Physical parameters of different phases.
参数 值 固体骨架颗粒密度/(kg·m–3) 2650 填充固体密度/(kg·m–3) 900 固体骨架颗粒体积模量/GPa 38.7 固体骨架颗粒剪切模量/GPa 39.6 填充固体体积模量/GPa 7.9 填充固体剪切模量/GPa 3.3 孔隙度 0.3 
下载: 导出CSV
-
[1] Biot M A 1956 J. Acoust. Soc. Am. 28 168
Google Scholar
[2] Biot M A 1956 J. Acoust. Soc. Am. 28 179
Google Scholar
[3] Biot M A 1962 J. Appl. Phys. 33 1482
Google Scholar
[4] Biot M A 1962 J. Acoust. Soc. Am. 34 1254
Google Scholar
[5] Plona T J 1980 Appl. Phys. Lett. 36 259
Google Scholar
[6] 王秀明, 张海澜, 王东 2005 地球 46 1206
Google Scholar
Wang X M, Zhang H L, Wang D 2005 Chin. J. Geophys. 46 1206
Google Scholar
[7] 刘财, 杨庆节, 鹿琪, 郭智奇, 刘洋, 兰慧田, 耿美霞, 王典 2014 地球 57 2885
Google Scholar
Liu C, Yang Q J, Lu Q, Guo Z Q, Liu Y, Lan H T, Geng M X, Wang D 2014 Chin. J. Geophys. 57 2885
Google Scholar
[8] Ba J, Carcione J M, Nie J X 2011 J. Geophys. Res. 116 B06202
Google Scholar
[9] 崔志文, 刘金霞, 王春霞, 王克协 2010 59 8655
Google Scholar
Cui Z W, Liu J X, Wang C X, Wang K X 2010 Acta Phys. Sin. 59 8655
Google Scholar
[10] 丁卫, 吴文雯, 王驰, 吴智强 2014 63 224301
Google Scholar
Ding W, Wu W W, Wang C, Wu Z Q 2014 Acta Phys. Sin. 63 224301
Google Scholar
[11] Ba J, Carcione J M, Sun W 2015 Geophys. J. Int. 202 1843
Google Scholar
[12] Ba J, Xu W, Fu L Y, Carcione J M, Zhang L 2017 J. Geophys. Res-Sol. Ea. 122 1949
Google Scholar
[13] 王婷, 崔志文, 刘金霞, 王克协 2018 67 114301
Google Scholar
Wang T, Cui Z W, Liu J X, Wang K X 2018 Acta Phys. Sin. 67 114301
Google Scholar
[14] 周永潮, 许恒磊, 陈佳代, 张仪萍, 唐耀, 彭宇 2022 岩土工程学报 44 255
Google Scholar
Zhou Y C, Xu H L, Chen J D, Zhang Y P, Tang Y, Peng Y 2022 Chin. J. Geotech. Eng. 44 255
Google Scholar
[15] 李好婷, 朱玉颖, 孔德, 张旭瞳, 王淑彦 2021 工程热 42 2017
Li H T, Zhu Y Y, Kong D, Zhang X T, Wang S Y 2021 J. Engine. The. 42 2017
[16] 秦雷 2018 北京信息科技大学学报 33 1
Google Scholar
Qin L 2018 J. Beijing Inform. Sci. & Tech. Uni. 33 1
Google Scholar
[17] 仲超 2019 博士学位论文 (北京: 北京邮电大学)
Zhong C 2019 Ph. D Dissertation (Beijing: Beijing University of Posts and Telecommunications) (in Chinese)
[18] Zhu X, McMechan G A 1990 Geophysics 56 328
Google Scholar
[19] Dai N, Vafidis A, Kanasewich E R 1995 Geophysics 60 327
Google Scholar
[20] Carcione J M, Quiroga-Goode G 1996 Geophys. Pros. 44 99
Google Scholar
[21] Atalla N, Panneton R, Debergue P 1996 J. Acoust. Soc. Am. 104 1444
[22] Panneton R, Atalla N 1997 J. Acoust. Soc. Am. 101 3287
Google Scholar
[23] 杜启振, 刘莲莲, 孙晶波 2007 56 6143
Google Scholar
Du Q Z, Liu L L, Sun J B 2007 Acta Phys. Sin. 56 6143
Google Scholar
[24] Zhao H B, Wang X M, Chen H 2006 Chin. Phys. 15 2819
Google Scholar
[25] Santos J E, Corberó J M, Douglas J 1990 J. Acoust. Soc. Am. 87 1428
Google Scholar
[26] Carcione J M, Seriani G 2001 J. Comput. Phys. 170 6765
Google Scholar
[27] Gao J H, Zhang Y J 2013 Math. Probl. Eng. 5 707
Google Scholar
[28] Zhang Y, Gao J, Peng J 2018 IEEE Trans. Geosci. Remote Sens. 56 2991
Google Scholar
[29] Zhan Q, Zhuang M, Mao Y, Liu Q H 2020 J. Comput. Phys. 402 108961
Google Scholar
[30] Liu L, Zhang X M, Wang X M 2021 Chin. Phys. B. 30 024301
Google Scholar
[31] 兰慧田, 刘财, 郭智奇 2014 世界地质 33 190
Google Scholar
Lan H Y, Liu C, Guo Z Q 2014 Global Geol. 33 190
Google Scholar
[32] Leclaire P, Cohen-Ténoudji F, Aguirre-Puente J 1994 J. Acoust. Soc. Am. 96 3753
Google Scholar
[33] Berryman J G, Wang H F 2000 Int. J. Rock Mech. Min. 37 63
Google Scholar
[34] Guerin G, Goldberg D 2005 Geochem. Geophy. Geosy. 6 1
Google Scholar
[35] Carcione J M, Gurevich B, Cavallini F 2000 Geophys. Prospect. 48 539
Google Scholar
下载:
计量
- 文章访问数: 4128
- PDF下载量: 94
- 被引次数: 0
