-
Bessel型光晶格是一种非空间周期性的柱对称的光晶格势场, 其兼具无限深势阱和环状势阱的特征, 在0阶Bessel光晶格势场中央形成深势阱, 而在非0阶Beseel光晶格势场中能形成具有中央势垒的环状浅势阱. 极化激元是一种半光半物质的准粒子, 该准粒子甚至可以在室温条件下发生玻色-爱因斯坦凝聚相变, 形成极化激元凝聚. 另外, 通过极化激元能级的腔诱导TE-TM分裂能在极化激元凝聚中实现足够强的自旋-轨道耦合作用. 极化激元凝聚能在室温条件下实现, 在其中又存在自旋-轨道耦合作用, 其为量子物理的研究提供了全新的平台. 本文把Bessel光晶格势场引入到极化激元凝聚系统, 研究了存在自旋-轨道耦合作用下的旋量双组分极化激元凝聚系统的稳态结构. 通过求解Gross-Pitaevskii方程给出了极化激元凝聚系统在实验室坐标系和旋转坐标系中极化激元凝聚系统的稳态结构, 由于Bessel势场的引入, 使得稳态结构更具有多样性. 给出了实验室坐标系中在中央深势阱中存在的基础型高斯孤立子、多极孤立子和在环状浅势阱中存在环状孤立子和多极孤立子的稳态结构; 给出了旋转坐标系中存在的涡旋环状孤立子, 及其由于自旋-轨道相互作用引起的组分分离的稳态结构. 分析了自旋-轨道耦合作用对两种坐标系中稳态结构的影响和多极孤立子在旋转坐标系中的稳定性. 结果表明, 环状浅势阱中形成的多极孤立子相对于中央深势阱中形成的多极孤立子具有更好的稳定性, 它们在旋转过程中能够长时间保持相对结构和空间分布不变. 在旋转坐标系中, 即使不满足双组分组分分离的条件, 由于自旋-轨道耦合作用的引入也能使得两组分发生组分分离.
Bessel optical lattice yields a non-spatially periodic column-symmetric optical lattice potential field, which has the characteristics of both infinite deep potential well and the ring-shaped potential well. A deep potential is formed in the center of the 0-order Bessel optical lattice. In the non-zero-order Beseel optical lattice, a ring-shaped shallow potential well with a central barrier can be formed. Exciton-polariton is a semi-light and semi-matter quasi-particle, which can achieve the Bose-Einstein condensate phase transition even at room temperature to form a polariton condensate. In addition, the polariton condensate is likely to realize sufficiently strong spin-orbit coupling due to the cavity-induced TE-TM splitting of the polariton energy levels. The polariton condensate can be realized at room temperature, and there can be spin-orbit coupling in it, which provides a new platform for the studying of quantum physics. In this paper, the Bessel optical lattice is introduced into a polariton condensate. The stationary state structure of spinor two-component polariton condensate with spin-orbit coupling is investigated. By solving the Gross-Pitaevskii equation, we first give a stationary state structures of the polariton condensate both in the laboratory coordinate frame and in the rotating coordinate frame. Owing to the introduction of the Bessel optical lattice, the stationary state structures of polariton condensate are diverse. We dispaly the stationary state structures of the basic Gaussian solitons and multipole solitons in the central deep potential well in the laboratory coordinate frame, and the ring solitons and multipole solitons in the central shallow potential well. We also dispaly the vortex ring soliton that exists in the rotating coordinate frame, and the stationary state structure of the component separation caused by the spin-orbit interaction. We analyze not only the influences of the spin-orbit coupling on the stationary state structures in the two coordinate frames, but also the stability of the multipole solitons in the rotating coordinate frame. It is found that the multipole solitons formed in the ring-shaped shallow potential well have better stability than in the central deep potential well, and they can maintain the relative structure and spatial distribution for a long time in the rotation process. In the rotating coordinate frame, even if the two-component separation conditions are not satisfied, the introduction of spin-orbit coupling can cause the two components to separate. -
Keywords:
- exciton-polariton condensates /
- Bessel optical lattice /
- soliton /
- stationary state
[1] Weisbuch C, Nishioka M, Ishikawa A, Arakawa Y 1992 Phys. Rev. Lett. 69 3314
Google Scholar
[2] Xu X R, Zhang Z D, Liang Z X 2020 Phys. Rev. A 102 033317
Google Scholar
[3] Christopoulos S, Baldassarri Höger von Högersthal G, Grundy A J D, Lagoudakis P G, Kavokin A V, Baumberg J J, Christmann G, Butté R, Feltin E, Carlin J F, Grandjean N 2007 Phys. Rev. Lett. 98 126405
Google Scholar
[4] Ma X K, Egorov O A, Schumacher S 2017 Phys. Rev. Lett. 118 157401
Google Scholar
[5] Roumpos G, Fraser M D, Löffler A, Höfling S, Forchel A, Yamamoto Y 2011 Nat. Phys. 7 129
[6] Carusotto I, Ciuti C 2013 Rev. Mod. Phys. 85 299
[7] Salerno M, Abdullaev F Kh, Gammal A, Tomio L 2016 Phys. Rev. A 94 043602
Google Scholar
[8] Galitski V, Spielman I B 2013 Nature 494 49
Google Scholar
[9] Osterloh K, Baig M, Santos L, Zoller P, Lewenstein M 2005 Phys. Rev. Lett. 95 010403
Google Scholar
[10] Gautam S, Adhikari S K 2018 Phys. Rev. A 97 013629
Google Scholar
[11] Matuszewski M, Liew T C H, Rubo Y G, Kavokin A V 2012 Phys. Rev. B 86 115321
Google Scholar
[12] Sala V G, Solnyshkov D D, Carusotto I, Jacqmin T, Lemaître A, Terças H, Nalitov A, Abbarchi M, Galopin E, Sagnes I, Bloch J, Malpuech G, Amo A 2015 Phys. Rev. X 5 011034
Google Scholar
[13] Bhat I A, Mithun T, Malomed B A, Porsezian K 2015 Phys. Rev. A 92 063606
Google Scholar
[14] Bardyn C E, Karzig T, Refael G, Liew T C H 2015 Phys. Rev. B 91 161413
Google Scholar
[15] Lobanov V E, Kartashov Y V, Konotop V V 2014 Phys. Rev. Lett. 112 180403
Google Scholar
[16] Kartashov Y V, Skryabin D V 2016 Opt. Lett. 41 5043
Google Scholar
[17] Zezyulin D A, Kartashov Y V, Skryabin D V, Shelykh I A 2018 ACS Photonics 5 3634
Google Scholar
[18] Mandel O, Greiner M, Widera A, Rom T, Hänsch T W, Bloch I 2003 Nature 425 937
Google Scholar
[19] Durnin J 1987 J. Opt. Soc. Am. A 4 651
Google Scholar
[20] Vasara A, Turunen J, Friberg A T 1989 J. Opt. Soc. Am. A 6 1748
Google Scholar
[21] Arlt J, Dholakia K 2000 Opt. Commun. 177 297
Google Scholar
[22] Kartashov Y V, Carretero-Gonzalez R, Malomed B A, Vysloukh V A, Torner L 2005 Phys. Rev. Lett. 94 043902
Google Scholar
[23] Mihalache D, Mazilu D, Lederer F, Malomed B A, Kartashov Y V, Crasovan L C, Torner L 2005 Phys. Rev. Lett. 95 023902
Google Scholar
[24] Dong L W, Wang J D, Wang H, Yin G Y 2009 Phys. Rev. A 79 013807
Google Scholar
[25] Kartashov Y V, Vysloukh V A, Torner L 2004 Phys. Rev. Lett. 93 093904
Google Scholar
[26] Chen H B, Hu S M 2013 Eur. Phys. J. D 67 225
Google Scholar
[27] Richard M, Kasprzak J, André R, Romestain R, Dang L S, Malpuech G, Kavokin A 2005 Phys. Rev.B 72 201301
Google Scholar
[28] Nalitov A V, Liew T C H, Kavokin A V, Altshuler B L, Rubo Y G 2017 Phys. Rev. Lett. 119 067406
Google Scholar
[29] Flayac H, Shelykh I A, Solnyshkov D D, Malpuech G 2010 Phys. Rev. B 81 045318
Google Scholar
[30] Dufferwiel S, Li F, Cancellieri E, Giriunas L, Trichet A A P, Whittaker D M, Walker P M, Fras F, Clarke E, Smith J M, Skolnick M S, Krizhanovskii D N 2015 Phys. Rev. Lett. 115 246401
Google Scholar
[31] Padhi B, Duboscq R, Niranjan A, Soni R K 2015 Eur. Phys. J. B 88 116
Google Scholar
[32] Sinha S, Castin Y 2001 Phys. Rev. Lett. 87 190402
Google Scholar
[33] Fetter A L 2009 Rev. Mod. Phys. 81 647
Google Scholar
[34] Muruganandam P, Adhikari S K 2009 Comput. Phys. Commun. 180 1888
Google Scholar
[35] Bao W Z, Cai Y Y 2013 Kinetic and Related Models 6 1
Google Scholar
[36] Wen L H, Zhang Y P, Feng J 2010 J. Phys. B: At. Mol. Opt. Phys. 43 225302
Google Scholar
[37] Timmermans E 1998 Phys. Rev. Lett. 81 5718
Google Scholar
[38] Moxley F I, Dowling J P, Dai W Z, Byrnes T 2016 Phys. Rev. A 93 053603
Google Scholar
-
图 1 不同阶数n的Bessel型光晶格势场的空间分布 (a)
$n=0$ ; (b)$n=1$ ; (c)$n=2$ ; (d)$n=3$ .$x, y\in [-8, 8]$ . 势场的数学表达式为$-V_0 {\rm{J}}_{n}^2(\sqrt{2 b}r)$ , 其中$V_0=1,\; b=0.5$ Fig. 1. The BL potential
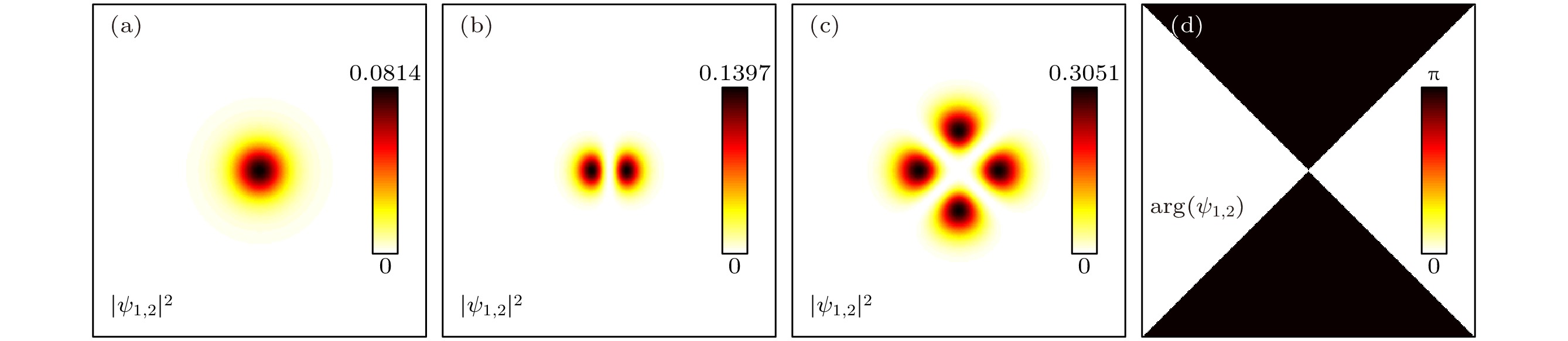
$-V_0 {\rm{J}}_{n}^2(\sqrt{2 b}r)$ with different n: (a)$n=0$ ; (b)$n=1$ ; (c)$n=2$ ; (d)$n=3$ .$x, y\in [-8, 8]$ ,$V_0=1,\; b=0.5$ 
图 2 0阶BL中央深势阱中的(a)高斯型孤立子、(b)偶极孤立子和(c)四极孤立子的密度分布; (d)与图(c)对应的相位分布. 图(a)和图(b)的计算范围是
$x, y\in [-8, 8]$ , 图(c)和图(d)的计算范围是$x, y\in [-3, 3]$ , BL参数分别是(a)$V_0=1$ ; (b)$V_0=4, $ $ b=0.4$ ; (c), (d)$V_0=20$ Fig. 2. Densities of (a) Gassian, (b) dipolar, (c) quadrupolar solitons and (d) the phase of the quadrupolar soliton in the central deep potential well of the BL, where
$x, y\in [-8, 8]$ for panels (a) and (b),$x, y\in [-3, 3]$ for panels (c) and (d). Values of other parameters are$V_0=1$ for panel (a),$V_0=4, b=0.4$ for panel (b),$V_0=20$ for panels (c) and (d).
图 3 BL环状浅势阱中极化激元凝聚环状孤立子稳态结构的密度分布
$|\psi_{1, 2}|^2$ 随阶数n的变化, 计算范围$x, y\in [-8, 8]$ , 角速率$\varOmega=0$ , SOC作用强度$\alpha=0$ . BL参数分别是 (a)$V_0=10,\; n=1$ ; (b)$V_0=10,\; n=2$ ; (c)$V_0=20, \;n=3$ Fig. 3. Densities
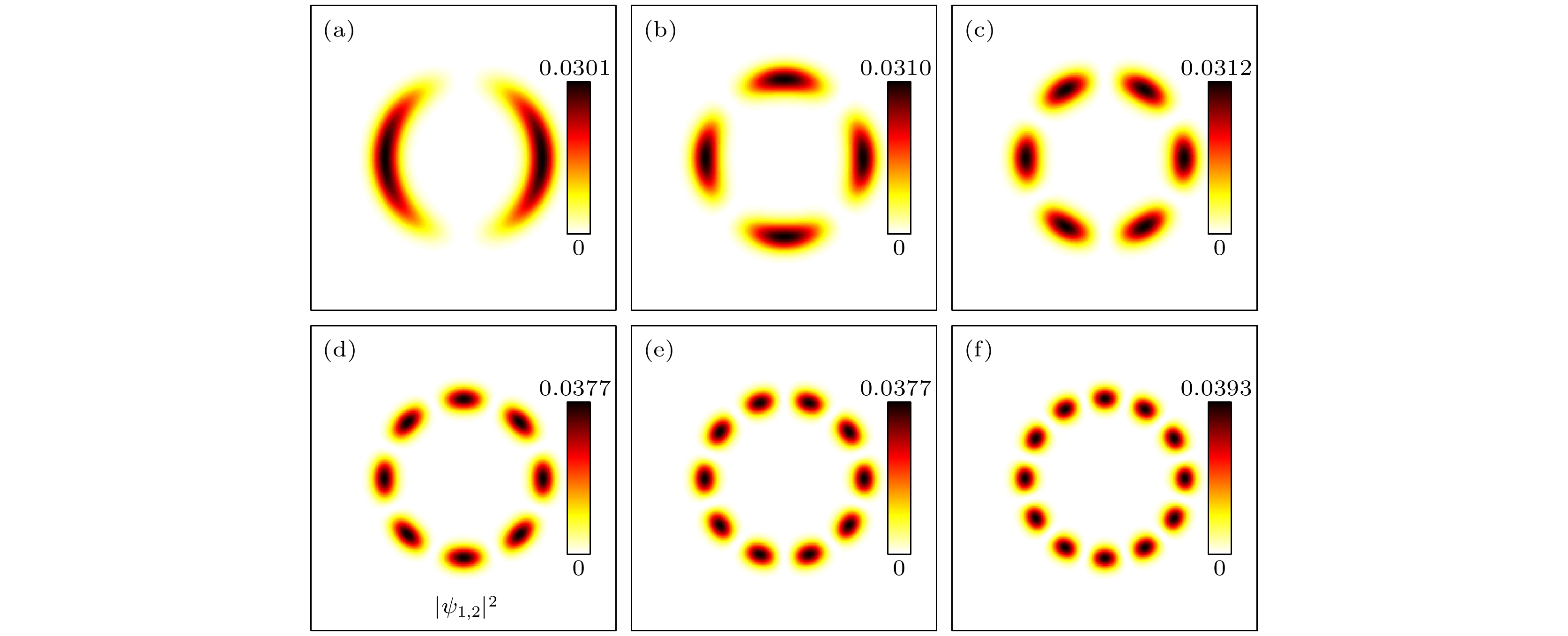
$|\psi_{1, 2}|^2$ of ring-shaped solitons in the ring-shaped shallow potential well of the BL with different$(V_0, n)$ : (a) (10, 1); (b) (10, 2); (c) (20, 3).$x, y\in [-8, 8]$ ,$\varOmega=0$ ,$\alpha=0$ .
图 4 BL环状浅势阱中极化激元凝聚多极孤立子稳态结构的密度分布
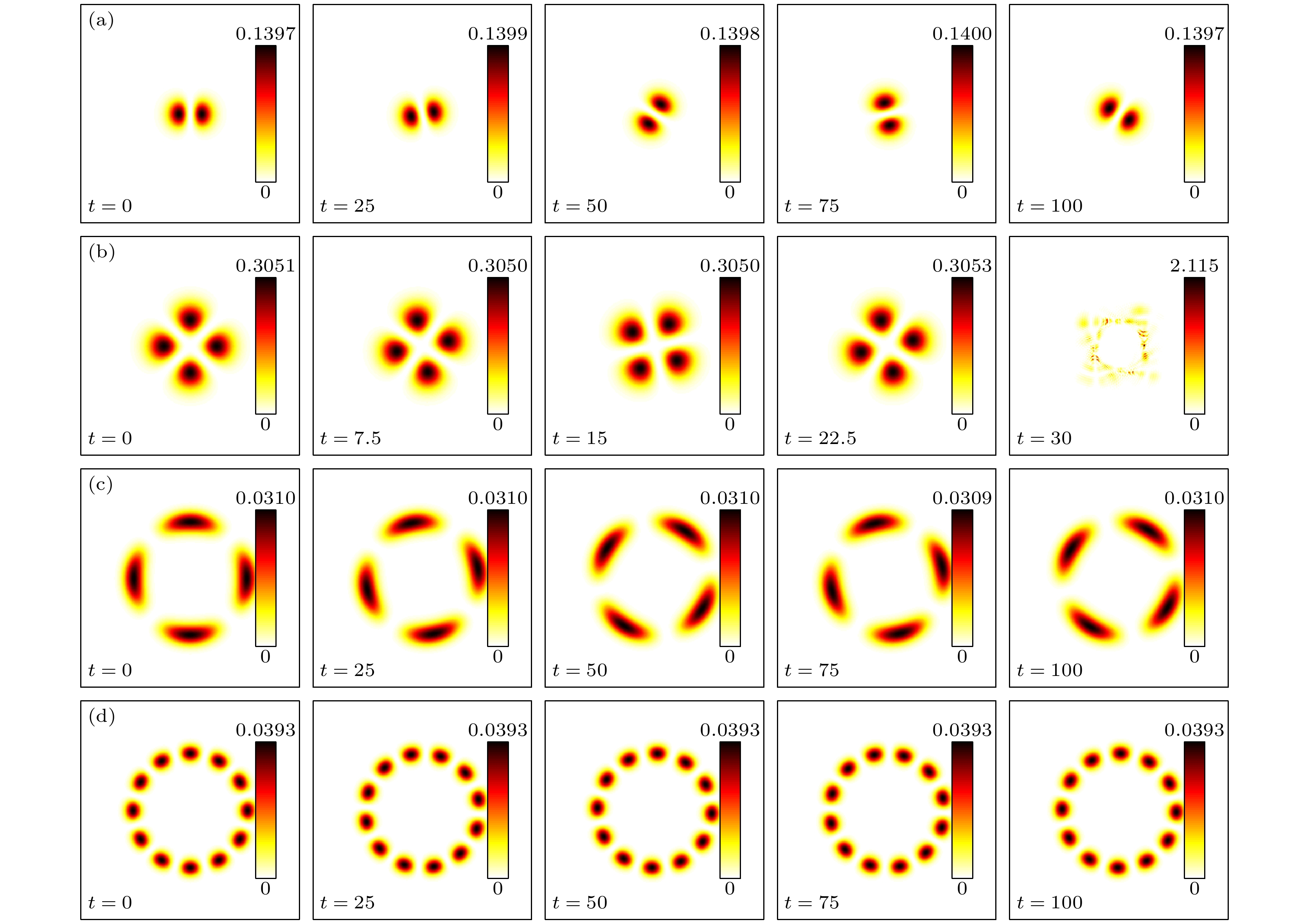
$|\psi_{1, 2}|^2$ , 计算范围$x, y\in [-8, 8]$ , 角速率$\varOmega=0$ , SOC作用强度$\alpha=0$ ,$n=3$ .$V_0$ 和$n_{\rm{p}}$ 分别是 (a)$V_0=30,\; n_{\rm{p}}=2$ ; (b)$V_0=30,\; n_{\rm{p}}=4$ ; (c)$V_0=30,\; n_{\rm{p}}=6$ ; (d)$V_0=60, \;n_{\rm{p}}=8$ ; (e)$V_0=60,\; n_{\rm{p}}=10$ ; (f)$V_0=70,\; n_{\rm{p}}=12$ Fig. 4. Densities (
$|\psi_{1, 2}|^2$ ) of multipole solitons in the ring-shaped shallow potential well of BL with different$(V_0, n_{\rm{p}})$ : (a) (30, 2); (b) (30, 4); (c) (30, 6); (d) (60, 8); (e) (60, 10); (f) (70, 12).$x, y\in [-8, 8]$ ,$\varOmega=0$ ,$\alpha=0$ ,$n=3$ .
图 5 BL势场中央深势阱中基础孤立子稳态结构的密度分布
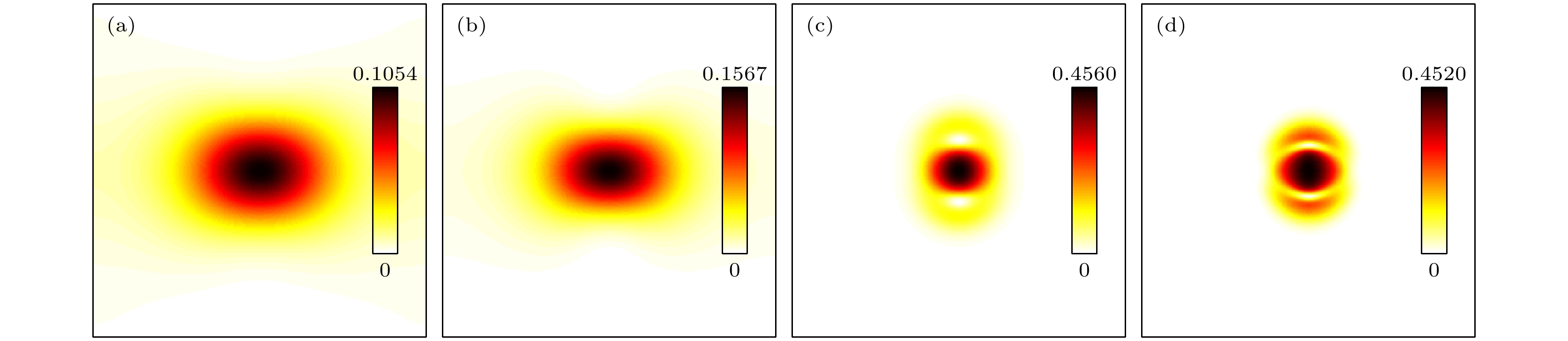
$|\psi_{1, 2}|^2$ 随SOC作用强度α的变化 (a)$\alpha=0.3$ ; (b)$\alpha=0.4$ ; (c)$\alpha=0.495$ ; (d)$\alpha=0.499$ . 计算范围$x, y\in [-3, 3]$ , BL参数为$V_0=1.0, n=0$ , 角速率$\varOmega=0$ Fig. 5. Densities
$|\psi_{1, 2}|^2$ of fundamental solitons in the central deep potential well of the BL with different α: (a)$\alpha=0.3$ ; (b)$\alpha=0.4$ ; (c)$\alpha=0.495$ ; (d)$\alpha=0.499$ .$x, y\in [-3, 3]$ ,$\varOmega=0$ ,$V_0=1.0, n=0$ .
图 6 存在SOC作用时, 不同阶数BL势场环状浅势阱中极化激元凝聚稳态结构的密度分布
$|\psi_{1, 2}|^2$ . 计算范围$x, y\in [-8, 8]$ , 角速率$\varOmega=0$ , SOC作用强度$\alpha=0.2$ . BL参数分别是 (a)$V_0=10,\; n=1$ ; (b)$V_0=10,\; n=2$ ; (c), (d)$V_0=20,\; n=3$ Fig. 6. In the presence of SOC, the densities (
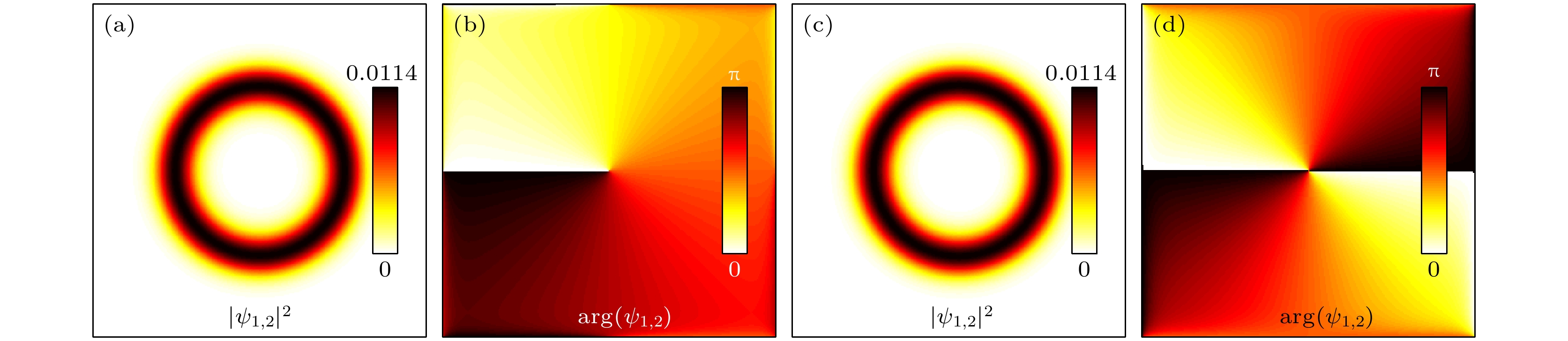
$|\psi_{1, 2}|^2$ ) of stationary state structures in the ring-shaped shallow potential well of the BL with different$V_0$ and n: (a)$V_0=10,\; n=1$ ; (b)$V_0=10,\; n=2$ ; (c), (d)$V_0=20,\; n=3$ .$x, y\in [-8, 8]$ ,$\varOmega=0$ ,$\alpha=0.2$ .
图 7 无SOC作用, 旋转坐标系中, 处于BL环状浅势阱中极化激元凝聚的涡旋孤立子结构的密度((a), (c))和相位((b), (d))分布, BL参数为
$V_0=10, n=3$ , 计算范围$x, y\in [-8, 8]$ ,$\alpha=0$ . 角速率分别是0.05((a), (b))和0.1((c), (d))Fig. 7. In the absence of SOC, the densities ((a), (c)) and phases ((b), (d)) vortex solitons in the ring-shaped shallow potential well of the BL in the rotating coordinate frame with different
$\varOmega $ (0.05 for panels (a) and (b), and 0.1 for panels (c) and (d)), where$x, y\in [-8, 8]$ ,$\alpha=0$ ,$V_0=10, n=3$ .
图 8 存在SOC作用时, 不同角速率下形成的涡旋孤立子的密度和相位分布 (a) –0.15; (b) 0; (c) 0.15. 计算范围
$x, y\in [-8, 8]$ ,$\alpha=0.1$ ,$V_0=10,\; n=3$ Fig. 8. In the presence of SOC, the densities and phases of vortex solitons in the ring-shaped shallow potential well of the BL with different
$\varOmega $ : (a) –0.15; (b) 0; (c) 0.15.$x, y\in [-8, 8]$ ,$V_0=10,\; n=3$ ,$\alpha=0.1$ .
图 9 BL势场的径向缩放因子b对中央深势阱中涡旋稳态结构的密度和相位的影响 (a)
$b=0.1$ ; (b)$b=0.2$ ; (c)$b=0.3$ ; (d)$b=0.4$ . 计算范围$x, y\in [-2, 2]$ , SOC作用强度$\alpha=0.4$ , BL参数为$V_0=40, n=0$ , 旋转角速率$\varOmega=0.95$ Fig. 9. Densities and phases of stationary vortex structures in the central deep potential of the BL with different b: (a)
$b=0.1$ ; (b)$b=0.2$ ; (c)$b=0.3$ ; (d)$b=0.4$ .$x, y\in [-2, 2]$ ,$\alpha=0.4$ ,$V_0=40, n=0$ ,$\varOmega=0.95$ .
图 10 BL势场中多极孤立子在旋转过程中, 密度分布
$|\psi_{1, 2}|^2$ 随时间变化, 旋转角速率为$\varOmega=0.1$ Fig. 10. Evolution dynamics of the multipolar solitions in the BL with
$\varOmega=0.1$ -
[1] Weisbuch C, Nishioka M, Ishikawa A, Arakawa Y 1992 Phys. Rev. Lett. 69 3314
Google Scholar
[2] Xu X R, Zhang Z D, Liang Z X 2020 Phys. Rev. A 102 033317
Google Scholar
[3] Christopoulos S, Baldassarri Höger von Högersthal G, Grundy A J D, Lagoudakis P G, Kavokin A V, Baumberg J J, Christmann G, Butté R, Feltin E, Carlin J F, Grandjean N 2007 Phys. Rev. Lett. 98 126405
Google Scholar
[4] Ma X K, Egorov O A, Schumacher S 2017 Phys. Rev. Lett. 118 157401
Google Scholar
[5] Roumpos G, Fraser M D, Löffler A, Höfling S, Forchel A, Yamamoto Y 2011 Nat. Phys. 7 129
[6] Carusotto I, Ciuti C 2013 Rev. Mod. Phys. 85 299
[7] Salerno M, Abdullaev F Kh, Gammal A, Tomio L 2016 Phys. Rev. A 94 043602
Google Scholar
[8] Galitski V, Spielman I B 2013 Nature 494 49
Google Scholar
[9] Osterloh K, Baig M, Santos L, Zoller P, Lewenstein M 2005 Phys. Rev. Lett. 95 010403
Google Scholar
[10] Gautam S, Adhikari S K 2018 Phys. Rev. A 97 013629
Google Scholar
[11] Matuszewski M, Liew T C H, Rubo Y G, Kavokin A V 2012 Phys. Rev. B 86 115321
Google Scholar
[12] Sala V G, Solnyshkov D D, Carusotto I, Jacqmin T, Lemaître A, Terças H, Nalitov A, Abbarchi M, Galopin E, Sagnes I, Bloch J, Malpuech G, Amo A 2015 Phys. Rev. X 5 011034
Google Scholar
[13] Bhat I A, Mithun T, Malomed B A, Porsezian K 2015 Phys. Rev. A 92 063606
Google Scholar
[14] Bardyn C E, Karzig T, Refael G, Liew T C H 2015 Phys. Rev. B 91 161413
Google Scholar
[15] Lobanov V E, Kartashov Y V, Konotop V V 2014 Phys. Rev. Lett. 112 180403
Google Scholar
[16] Kartashov Y V, Skryabin D V 2016 Opt. Lett. 41 5043
Google Scholar
[17] Zezyulin D A, Kartashov Y V, Skryabin D V, Shelykh I A 2018 ACS Photonics 5 3634
Google Scholar
[18] Mandel O, Greiner M, Widera A, Rom T, Hänsch T W, Bloch I 2003 Nature 425 937
Google Scholar
[19] Durnin J 1987 J. Opt. Soc. Am. A 4 651
Google Scholar
[20] Vasara A, Turunen J, Friberg A T 1989 J. Opt. Soc. Am. A 6 1748
Google Scholar
[21] Arlt J, Dholakia K 2000 Opt. Commun. 177 297
Google Scholar
[22] Kartashov Y V, Carretero-Gonzalez R, Malomed B A, Vysloukh V A, Torner L 2005 Phys. Rev. Lett. 94 043902
Google Scholar
[23] Mihalache D, Mazilu D, Lederer F, Malomed B A, Kartashov Y V, Crasovan L C, Torner L 2005 Phys. Rev. Lett. 95 023902
Google Scholar
[24] Dong L W, Wang J D, Wang H, Yin G Y 2009 Phys. Rev. A 79 013807
Google Scholar
[25] Kartashov Y V, Vysloukh V A, Torner L 2004 Phys. Rev. Lett. 93 093904
Google Scholar
[26] Chen H B, Hu S M 2013 Eur. Phys. J. D 67 225
Google Scholar
[27] Richard M, Kasprzak J, André R, Romestain R, Dang L S, Malpuech G, Kavokin A 2005 Phys. Rev.B 72 201301
Google Scholar
[28] Nalitov A V, Liew T C H, Kavokin A V, Altshuler B L, Rubo Y G 2017 Phys. Rev. Lett. 119 067406
Google Scholar
[29] Flayac H, Shelykh I A, Solnyshkov D D, Malpuech G 2010 Phys. Rev. B 81 045318
Google Scholar
[30] Dufferwiel S, Li F, Cancellieri E, Giriunas L, Trichet A A P, Whittaker D M, Walker P M, Fras F, Clarke E, Smith J M, Skolnick M S, Krizhanovskii D N 2015 Phys. Rev. Lett. 115 246401
Google Scholar
[31] Padhi B, Duboscq R, Niranjan A, Soni R K 2015 Eur. Phys. J. B 88 116
Google Scholar
[32] Sinha S, Castin Y 2001 Phys. Rev. Lett. 87 190402
Google Scholar
[33] Fetter A L 2009 Rev. Mod. Phys. 81 647
Google Scholar
[34] Muruganandam P, Adhikari S K 2009 Comput. Phys. Commun. 180 1888
Google Scholar
[35] Bao W Z, Cai Y Y 2013 Kinetic and Related Models 6 1
Google Scholar
[36] Wen L H, Zhang Y P, Feng J 2010 J. Phys. B: At. Mol. Opt. Phys. 43 225302
Google Scholar
[37] Timmermans E 1998 Phys. Rev. Lett. 81 5718
Google Scholar
[38] Moxley F I, Dowling J P, Dai W Z, Byrnes T 2016 Phys. Rev. A 93 053603
Google Scholar
下载:
计量
- 文章访问数: 3758
- PDF下载量: 72
- 被引次数: 0
