-
磁共振测深法(magnetic resonance sounding, MRS)具有无需钻探即可直接探测地下水含量的优势, 但是极低的信噪比(signal-to-noise ratio, SNR)限制了该方法的大范围应用, 目前的研究工作主要集中在消除MRS信号中的尖峰噪声和工频谐波噪声上, 而随机噪声由于其无规律性导致难以消除, 但是它的影响不容忽视. 目前MRS随机噪声的消减常采用叠加法, 需要重复采集数据叠加平均来达到消噪目的, 探测时间长且消噪效果有限. 针对这一问题, 本文提出了一种改进的短时傅里叶变换方法, 该方法通过处理单次采集的MRS包络信号来降低数据量, 提高数据处理效率. 改进的短时傅里叶变换方法采用解析信号代替常规短时傅里叶变换中的实值信号, 提高MRS信号时频域瞬时幅度的准确度, 得到MRS信号的高精度时频分布, 然后提取时频域峰值幅度和峰值相位重构信号来消除随机噪声. 仿真实验和实测数据处理结果表明, 该方法能够直接处理单次采集数据, 在信噪比高于–17.21 dB的情况下可有效提取MRS信号, 实现随机噪声的压制, 且与传统叠加法相比, 信噪比最多可提高27.88 dB, 均方根误差最多缩小36.44倍, 参数估计值更加准确. 本文的研究结果为利用MRS获取准确的地下水分布情况奠定了良好的基础.Magnetic resonance sounding (MRS) has the advantage of detecting groundwater content directly without drilling, but the signal-to-noise ratio (SNR) is extremely low which limits the application of the method. Most of the current researches focus on eliminating spikes and powerline harmonic noise in the MRS signal, whereas the influence of random noise cannot be ignored even though it is difficult to suppress due to the irregularity. The common method to eliminate MRS random noise is stacking which requires extensive measurement repetition at the cost of detection efficiency, and it is insufficient when employed in a high-level noise surrounding. To solve this problem, we propose a modified short-time Fourier transform(MSTFT) method, in which used is the short-time Fourier transform on the analytical signal instead of the real-valued signal to obtain the high-precision time-frequency distribution of MRS signal, followed by extracting the time-frequency domain peak amplitude and peak phase to reconstruct the signal and suppress the random noise. The performance of the proposed method is tested on synthetic envelope signals and field data. The using of the MSTFT method to handle a single recording can suppress the random noise and extract MRS signals when SNR is more than –17.21 dB. Compared with the stacking method, the MSTFT achieves an 27.88dB increase of SNR and more accurate parameter estimation. The findings of this study lay a good foundation for obtaining exact groundwater distribution by utilizing magnetic resonance sounding.
-
Keywords:
- MRS /
- random noise /
- modified short-time Fourier transform /
- data processing
[1] 林君, 段清明, 王应吉 2011 核磁共振找水仪原理与应用 (北京: 科学出版社) 第2−10页
Lin J, Duan Q M, Wang Y J 2011 Theory and Design of Magnetic Resonance Sounding Instrument for Groundwater Detection and Its Applications (Beijing: Science Press) pp2−10 (in Chinese)
[2] Legchenko A, Valla P 2002 J. Appl. Geophys. 50 3
Google Scholar
[3] Behroozmand A A, Keating K, Auken E 2015 Surv. Geophys. 36 27
Google Scholar
[4] Legchenko A, Valla P 1998 J. Appl. Geophys. 39 77
Google Scholar
[5] Legchenko A, Baltassat J M, Beauce A, Berbard J 2002 J. Appl. Geophys. 50 21
Google Scholar
[6] Hertrich M 2008 Prog. Nucl. Magn. Reson. Spectrosc. 53 227
Google Scholar
[7] Walsh D, Turner P, Grunewald E, Zhang H, Butler J J, Reboulet E, Knobbe S, Christy T, Lane J W, Johnson C D, Munday T, Fitzpatrick A 2013 Ground Water 51 914
Google Scholar
[8] Dlugosch R, Günther T, Lukàcs T, Müller-Petke M 2016 Geophysics 81 WB109
Google Scholar
[9] Grunewald E, Grombacher D, Walsh D 2016 Geophysics 81 WB85
Google Scholar
[10] 林君, 张扬, 张思远, 舒旭, 杜文元, 林婷婷 2016 吉林大学学报(地球科学版) 46 1221
Google Scholar
Lin J, Zhang Y, Zhang S Y, Shu X, Du W Y, Lin T T 2016 J. Jilin Univ. (Earth Science Edition) 46 1221
Google Scholar
[11] Lin J, Zhang Y, Yang Y J, Sun Y, Lin T T 2017 Rev. Sci. Instrum. 88 064702
Google Scholar
[12] Davis A C, Dlugosch R, Queitsch M, Macnae J C, Stolz R, Müller-Petke 2014 Geophys. Res. Lett. 41 4222
Google Scholar
[13] Davis A C, Müller-Petke M, Dlugosch R, Quietsch M, Macnae J, Stolz R 2015 ASEG Extended Abstracts 2015 1
Google Scholar
[14] Lin T T, Yang Y J, Teng F, Müller-Petke M 2018 Geophys. J. Int. 212 1463
Google Scholar
[15] Müller-Petke M, Braun M, Hertrich M, Costabel S, Walbrecker J 2016 Geophysics 81 WB9
Google Scholar
[16] Jiang C D, Lin J, Duan Q M, Sun S Q, Tian B F 2011 Near Surf. Geophys. 9 459
Google Scholar
[17] Dalgaard E, Auken E, Larsen J J 2012 Geophys. J. Int. 191 88
Google Scholar
[18] Larsen J J 2016 Geophysics 81 WB1
Google Scholar
[19] Legchenko A, Valla P 2003 J. Appl. Geophys. 53 103
Google Scholar
[20] Walsh D O 2008 J. Appl. Geophys. 66 140
Google Scholar
[21] Müller-Petke M, Costabel S 2014 Near Surf. Geophys. 12 199
Google Scholar
[22] Larsen J J, Dalgaard E, Auken E 2014 Geophys. J. Int. 196 828
Google Scholar
[23] Dalgaard E, Müller-Petke M, Auken E 2016 Near Surf. Geophys. 14 243
Google Scholar
[24] 林婷婷, 张扬, 杨莹, 杨玉晶, 滕飞, 万玲 2018 地球 561 3812
Google Scholar
Lin T T, Zhang Y, Yang Y, Yang Y J, Teng F, Wan L 2018 Chinese J. Geophys. 561 3812
Google Scholar
[25] Bernard J. 2006 Proceedings of the 3rd Magnetic Resonance Sounding International Workshop Madrid, Spain, October 25−27, 2006 p459
[26] 段一斌 2014 硕士学位论文 (成都: 电子科技大学)
Duan Y B 2014 M. S. Thesis (Chengdu: University of Electronic Science and Technology of China) (in Chinese)
[27] Marfurt K J, Kirlin R L 2001 Geophysics 66 1274
Google Scholar
[28] Behroozmand A A, Dalgaard E, Christiansen A V, Auken E 2013 Near Surf. Geophys. 11 557
Google Scholar
-
图 1 叠加法分别叠加1, 4, 8和16次时消除随机噪声效果时域和频域图
Fig. 1. Time-domain and frequency-domain diagrams after stacking 1, 4, 8 and 16 times to suppress random noise, respectively.
图 2 MSTFT与常规短时傅里叶变换之间的区别 (a) 时频幅度谱
${A_{\rm{s}}}\left( {\tau, f} \right)$ ; (b) 时频相位谱${\theta _{\rm{s}}}\left( {\tau, f} \right)$ ; (c) 高精度时频幅度谱$A\left( {\tau, f} \right)$ ; (d) 高精度时频相位谱$\theta \left( {\tau, f} \right)$ ; (e)${A_{\rm{s}}}\left( {\tau, f} \right)$ 和$A\left( {\tau, f} \right)$ 的差异; (f)${\theta _{\rm{s}}}\left( {\tau, f} \right)$ 和$\theta \left( {\tau, f} \right)$ 的差异Fig. 2. Difference between the MSTFT and the conventional short-time Fourier transform: (a) time–frequency amplitude spectrum
${A_{\rm{s}}}\left( {\tau, f} \right)$ ; (b) time–frequency phase spectrum${\theta _{\rm{s}}}\left( {\tau, f} \right)$ ; (c) high-precision time–frequency amplitude spectrum$A\left( {\tau, f} \right)$ ; (d) high-precision time–frequency phase spectrum$\theta \left( {\tau, f} \right)$ ; (e) difference between${A_{\rm{s}}}\left( {\tau, f} \right)$ and$A\left( {\tau, f} \right)$ ; (f) difference between${\theta _{\rm{s}}}\left( {\tau, f} \right)$ and$\theta \left( {\tau, f} \right)$ .
图 3 MSTFT方法消除随机噪声过程示例 (a) 仿真含噪数据; (b)瞬时幅度; (c) 瞬时相位; (d) 峰值幅度; (e) 峰值相位; (f)重构信号
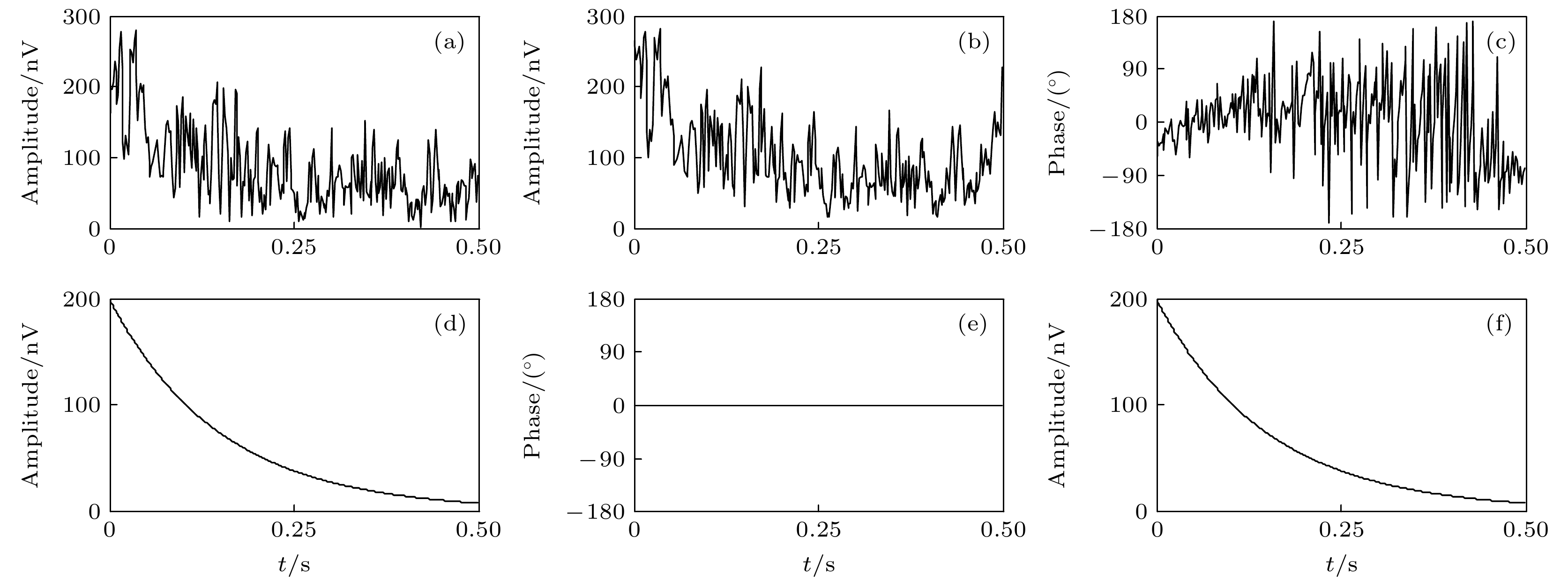
Fig. 3. Example of the basic procedure for the random noise suppression using MSTFT: (a) Synthetic noisy signal; (b) instantaneous amplitude; (c) instantaneous phase; (d) peak amplitude; (e) peak phase; (f) reconstructed signal.
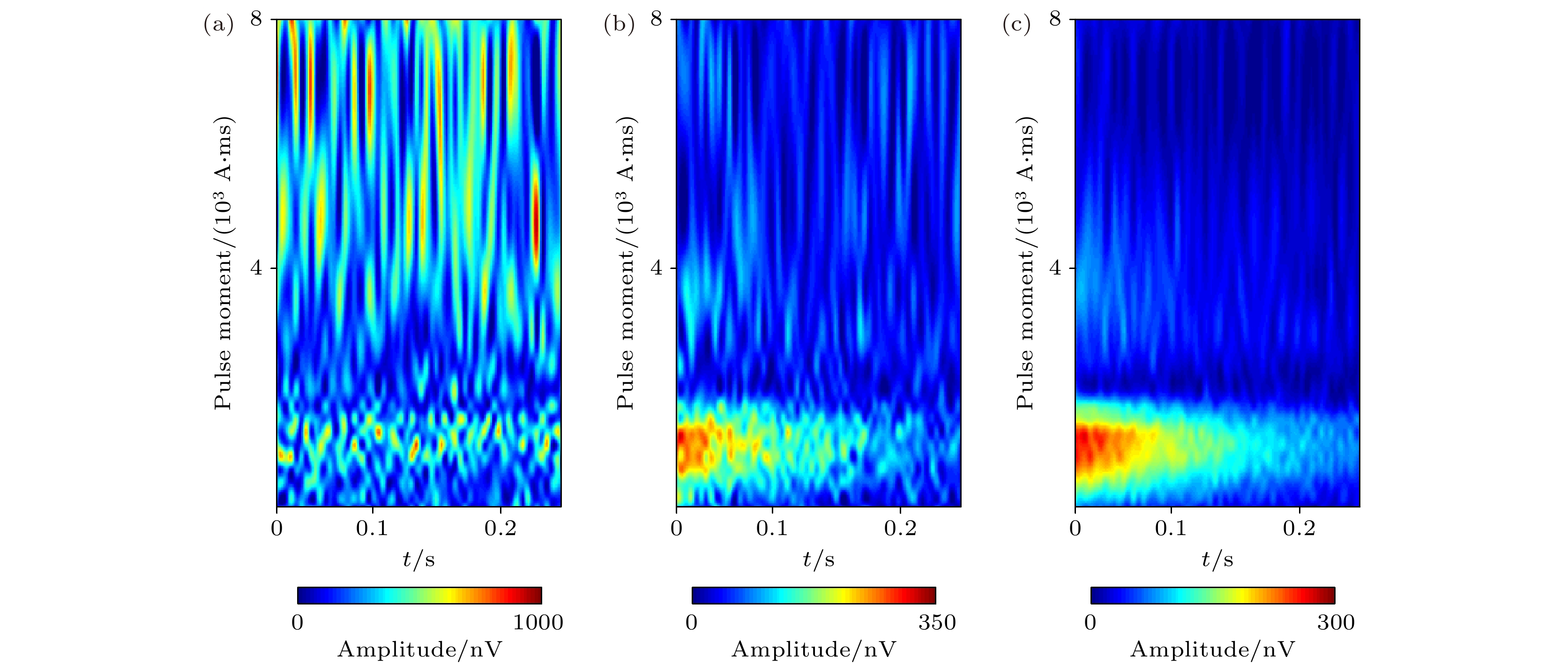
图 4 3组仿真随机噪声消噪结果图 (a)低噪声强度下仿真数据高精度时频域振幅; (b) 低噪声强度下消噪结果时域图; (c) 低噪声强度下消噪结果频域图; (d) 中噪声强度下仿真数据高精度时频域振幅; (e) 中噪声强度下消噪结果时域图; (f) 中噪声强度下消噪结果频域图; (g) 高噪声强度下仿真数据高精度时频域振幅; (h) 高噪声强度下消噪结果时域图; (i) 高噪声强度下消噪结果频域图
Fig. 4. The de-noising results of 3 sets of random noise simulation: (a) High-precision time-frequency domain amplitude of simulated data under low noise intensity; (b) time domain results under low noise intensity; (c) frequency domain results under low noise intensity; (d) high-precision time-frequency domain amplitude of simulated data under moderate noise intensity; (e) time domain results under moderate noise intensity; (f) frequency domain results under moderate noise intensity; (g) high-precision time-frequency domain amplitude of simulated data under high noise intensity; (h) time domain results under high noise intensity; (i) frequency domain results under high noise intensity.
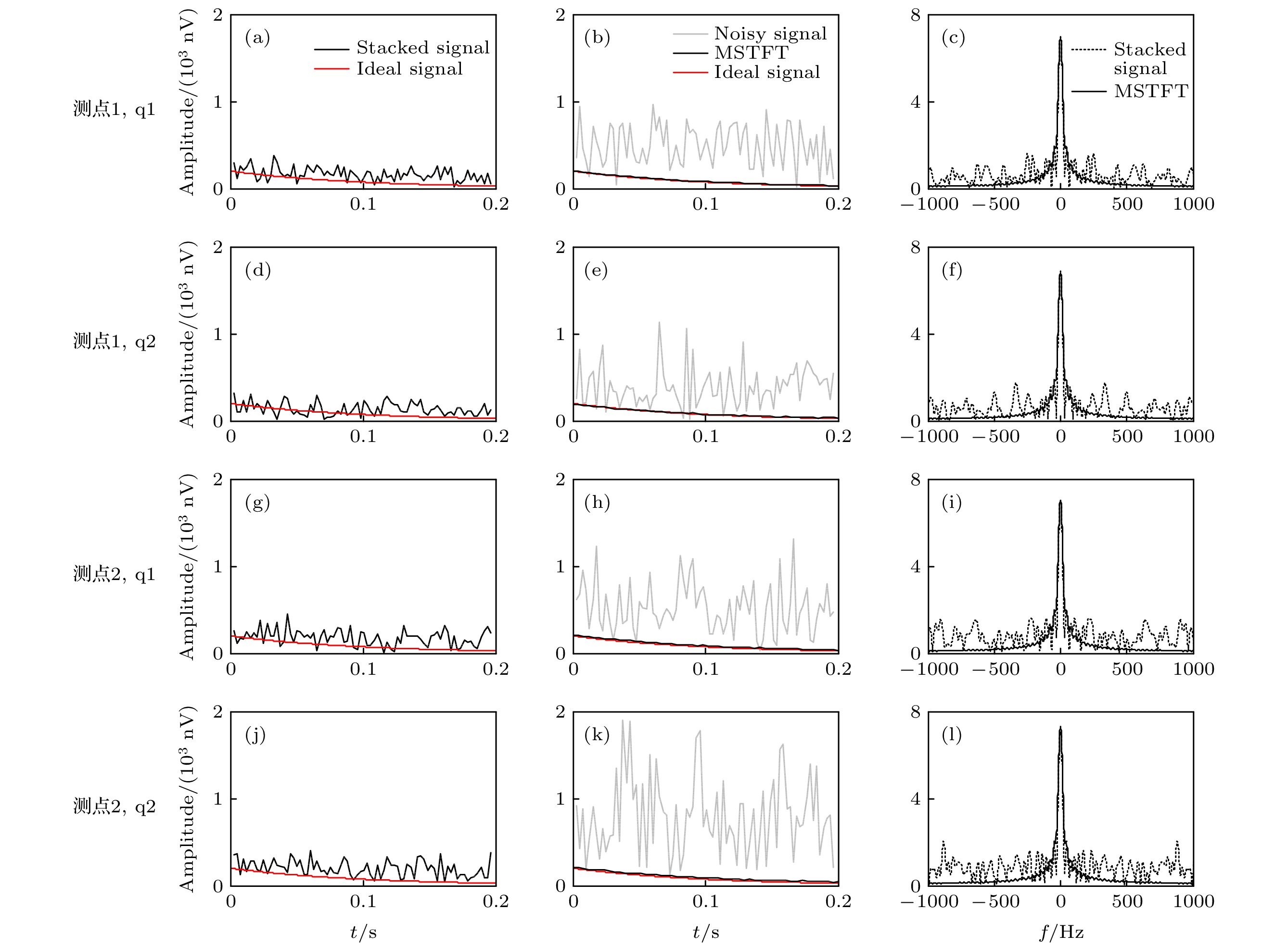
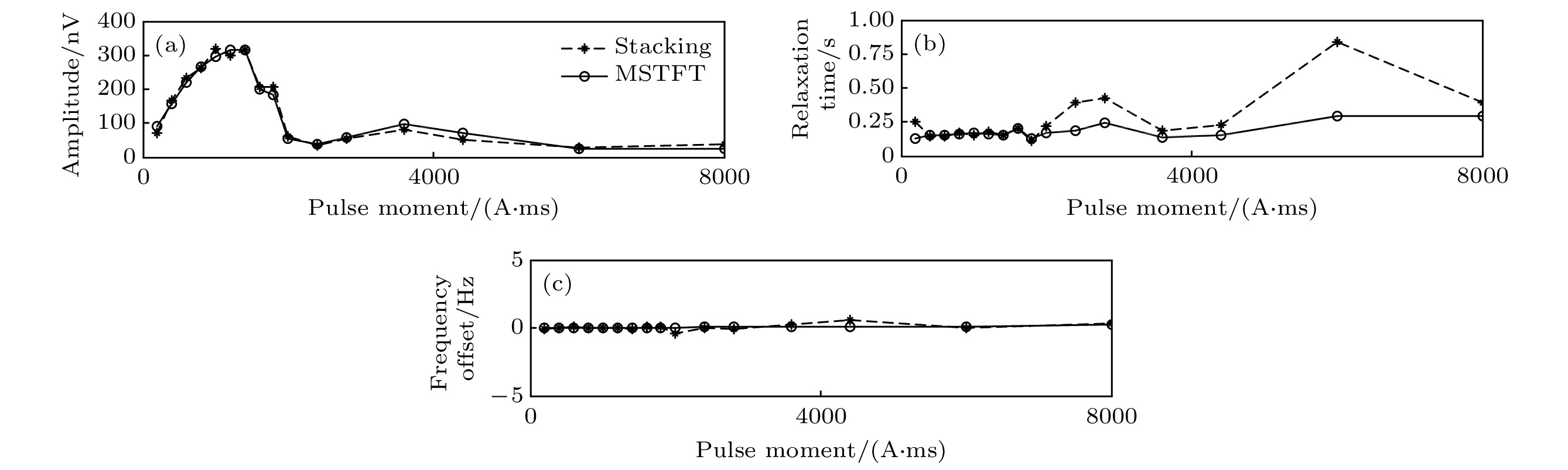
图 5 叠加法和MSTFT方法消除随机噪声效果对比图 (a) 叠加法消除随机噪声时域图; (b) MSTFT方法消除随机噪声时域图; (c) 叠加法和MSTFT方法消除随机噪声频域对比图
Fig. 5. Comparison of the de-noising results by using stacking and MSTFT methods: (a) Results of random noise elimination by stacking in time domain; (b) results of random noise elimination by MSTFT in time domain; (c) comparison of the de-noising results by using stacking and MSTFT methods in frequency domain.
图 6 实测数据处理结果图 (a) 野外探测原始数据; (b) 叠加法消除随机噪声后数据; (c) MSTFT方法消除随机噪声后数据
Fig. 6. De-noising results of field data: (a) Original field data; (b) random noise elimination by stacking; (c) random noise elimination by MSTFT.
图 7 叠加法和MSTFT方法处理4个脉冲矩信号结果对比图 (a) 时域对比结果; (b) 频域对比结果
Fig. 7. Comparison of the de-noising results of 4 pulse moments by using stacking and MSTFT methods: (a) Time domain comparison; (b) frequency domain comparison.
图 8 叠加法和MSTFT处理实测数据提取参数结果对比 (a) 初始振幅; (b) 弛豫时间; (c) 频率偏移
Fig. 8. Parameter estimation after random noise elimination of field data by using stacking and MSTFT methods: (a) Initial amplitude; (b) relaxation time; (c) frequency offset.
图 9 叠加法和MSTFT处理实测数据提取MRS信号反演结果与钻孔结果对比 (a) 叠加法; (b) MSTFT方法
Fig. 9. Comparison of the inversion of the field data processd by stacking and MSTFT methods respectively with the borehole log: (a) Stacking result; (b) MSTFT result.
表 1 3组仿真随机噪声消噪后参数估计情况表
Table 1. The parameter estimation after de-noising of 3 sets of simulated random noise.
E0/nV $T_2^* $ /ms $\Delta f$ / Hz SNR/dB RMSE/nV 信号1
(SNR = 0.68 dB)200.19 ± 3.01 149.2 ± 2.8 –0.03 ± 0.01 32.67 1.03 ± 0.55 信号2
(SNR = –5.20 dB)202.61 ± 4.90 152.0 ± 6.7 0.04 ± 0.03 24.01 3.79 ± 1.89 信号3
(SNR = –11.22 dB)204.12 ± 5.96 154.4 ± 12.8 0.04 ± 0.06 20.81 5.81 ± 2.42 
下载: 导出CSV
表 2 叠加法和MSTFT消除随机噪声提取参数结果对比
Table 2. Comparison of the parameter estimation after random noise elimination by stacking and MSTFT methods.
E0/nV $T_2^* $ /ms $\Delta f$/Hz SNR/dB RMSE/nV 测点1: q1 16次叠加 167.49 270.1 –0.53 –16.81 484.95 MSTFT 197.42 ± 4.41 102.6 ± 5.3 –0.31 ± 0.09 11.07 13.31 ± 8.09 测点1: q2 16次叠加 163.78 285.5 –0.65 –16.85 487.52 MSTFT 195.77 ± 5.02 103.9 ± 5.9 –0.34 ± 0.10 9.83 19.10 ± 10.83 测点2: q1 32次叠加 217.43 336.9 –0.74 –17.05 498.41 MSTFT 205.20 ± 6.25 105.7 ± 8.7 –0.36 ± 0.11 8.08 24.31 ± 12.36 测点2: q2 32次叠加 221.51 359.4 –0.92 –17.21 507.79 MSTFT 206.21 ± 7.47 107.4 ± 10.9 –0.37 ± 0.11 6.91 27.70 ± 18.64
下载: 导出CSV
-
[1] 林君, 段清明, 王应吉 2011 核磁共振找水仪原理与应用 (北京: 科学出版社) 第2−10页
Lin J, Duan Q M, Wang Y J 2011 Theory and Design of Magnetic Resonance Sounding Instrument for Groundwater Detection and Its Applications (Beijing: Science Press) pp2−10 (in Chinese)
[2] Legchenko A, Valla P 2002 J. Appl. Geophys. 50 3
Google Scholar
[3] Behroozmand A A, Keating K, Auken E 2015 Surv. Geophys. 36 27
Google Scholar
[4] Legchenko A, Valla P 1998 J. Appl. Geophys. 39 77
Google Scholar
[5] Legchenko A, Baltassat J M, Beauce A, Berbard J 2002 J. Appl. Geophys. 50 21
Google Scholar
[6] Hertrich M 2008 Prog. Nucl. Magn. Reson. Spectrosc. 53 227
Google Scholar
[7] Walsh D, Turner P, Grunewald E, Zhang H, Butler J J, Reboulet E, Knobbe S, Christy T, Lane J W, Johnson C D, Munday T, Fitzpatrick A 2013 Ground Water 51 914
Google Scholar
[8] Dlugosch R, Günther T, Lukàcs T, Müller-Petke M 2016 Geophysics 81 WB109
Google Scholar
[9] Grunewald E, Grombacher D, Walsh D 2016 Geophysics 81 WB85
Google Scholar
[10] 林君, 张扬, 张思远, 舒旭, 杜文元, 林婷婷 2016 吉林大学学报(地球科学版) 46 1221
Google Scholar
Lin J, Zhang Y, Zhang S Y, Shu X, Du W Y, Lin T T 2016 J. Jilin Univ. (Earth Science Edition) 46 1221
Google Scholar
[11] Lin J, Zhang Y, Yang Y J, Sun Y, Lin T T 2017 Rev. Sci. Instrum. 88 064702
Google Scholar
[12] Davis A C, Dlugosch R, Queitsch M, Macnae J C, Stolz R, Müller-Petke 2014 Geophys. Res. Lett. 41 4222
Google Scholar
[13] Davis A C, Müller-Petke M, Dlugosch R, Quietsch M, Macnae J, Stolz R 2015 ASEG Extended Abstracts 2015 1
Google Scholar
[14] Lin T T, Yang Y J, Teng F, Müller-Petke M 2018 Geophys. J. Int. 212 1463
Google Scholar
[15] Müller-Petke M, Braun M, Hertrich M, Costabel S, Walbrecker J 2016 Geophysics 81 WB9
Google Scholar
[16] Jiang C D, Lin J, Duan Q M, Sun S Q, Tian B F 2011 Near Surf. Geophys. 9 459
Google Scholar
[17] Dalgaard E, Auken E, Larsen J J 2012 Geophys. J. Int. 191 88
Google Scholar
[18] Larsen J J 2016 Geophysics 81 WB1
Google Scholar
[19] Legchenko A, Valla P 2003 J. Appl. Geophys. 53 103
Google Scholar
[20] Walsh D O 2008 J. Appl. Geophys. 66 140
Google Scholar
[21] Müller-Petke M, Costabel S 2014 Near Surf. Geophys. 12 199
Google Scholar
[22] Larsen J J, Dalgaard E, Auken E 2014 Geophys. J. Int. 196 828
Google Scholar
[23] Dalgaard E, Müller-Petke M, Auken E 2016 Near Surf. Geophys. 14 243
Google Scholar
[24] 林婷婷, 张扬, 杨莹, 杨玉晶, 滕飞, 万玲 2018 地球 561 3812
Google Scholar
Lin T T, Zhang Y, Yang Y, Yang Y J, Teng F, Wan L 2018 Chinese J. Geophys. 561 3812
Google Scholar
[25] Bernard J. 2006 Proceedings of the 3rd Magnetic Resonance Sounding International Workshop Madrid, Spain, October 25−27, 2006 p459
[26] 段一斌 2014 硕士学位论文 (成都: 电子科技大学)
Duan Y B 2014 M. S. Thesis (Chengdu: University of Electronic Science and Technology of China) (in Chinese)
[27] Marfurt K J, Kirlin R L 2001 Geophysics 66 1274
Google Scholar
[28] Behroozmand A A, Dalgaard E, Christiansen A V, Auken E 2013 Near Surf. Geophys. 11 557
Google Scholar
下载:
计量
- 文章访问数: 4626
- PDF下载量: 78
- 被引次数: 0
