-
利用双色双光子阿秒干涉光谱可以在阿秒量级上精确测量光电子从原子、分子以及固体中的电离时间, 为人们理解激光辅助单光子电离中的光电子超快发射过程提供了前所未有的推动作用. 理解光电子发射时间依赖于物理模型, 而目前的模型在预测光电子发射时间上有很大的偏差. 于是, 本文对之前的程函近似模型进行了改进. 与之前的程函近似模型相比, 本文模型使用了更准确的末态波函数, 并且在计算光电子传播过程中累积的相位时, 更准确地计算了光电子轨迹, 因而可以更准确地预测光电子发射时间. 对比得到的数值模拟结果表明, 改进后的程函近似模型比以前的理论模型更加接近含时薛定谔方程的结果, 加深了我们对光电子发射超快过程的理解.The emission time of photoelectrons from atoms, molecules and solids can be accurately measured on an attosecond scale by using two-color two-photon attosecond interferometric spectroscopy, which helps us to understand the ultrafast electronic dynamics in laser-assisted single photoionization. Understanding the photoelectron emission time depends on the physical model, and the relevant theoretical model provides a better physical explanation and numerical prediction for the photoemission time delay. Although the numerical solution of the time-dependent Schrödinger equation can accurately predict the photoelectron emission time, but it cannot provide a physical explanation. Although some other current theoretical models can provide a more reasonable corresponding physical process, the quantitative prediction of the photoemission time delay has a large deviation. Therefore, we improve the exisating eikonal approximation model. Comparing with the existing eikonal approximation model, we use a more accurate final state wave function and calculate the photoelectron trajectory more accurately when calculating the phase accumulated in the photoelectron propagation process, so we can predict the photoemission time delay more accurately. By comparing our numerical simulation results, we find that when the final kinetic energy of photoelectron is low, the calculated results from the existing theoretical model are greatly different from those from the time-dependent Schrödinger equation, reaching tens of attoseconds. The resultsfrom the existing theoretical model are closer to those from the time-dependent Schrödinger equation with the increase of final kinetic energy of photoelectron. However, no matter what the final kinetic energy of the photoelectron is, the difference between the calculation result from the improved eikonal approximation model and that from the time-dependent Schrödinger equation is always very small. Therefore, our improved eikonal approximation model is closer to the results from the time-dependent Schrödinger equation than the existing theoretical model, which greatly deeps our understanding of the ultra-fast process of photoelectron emission.
-
Keywords:
- two-color two-photon /
- attosecond interference /
- time-dependent Schrödinger equation /
- eikonal approximation model
[1] Paul P M, Toma E S, Breger P, Mullot G, Auge F, Balcou Ph, Muller H G, Agostini P 2001 Science 292 1689
Google Scholar
[2] Muller H G 2002 Appl. Phys. B 74 s17
Google Scholar
[3] Klünder K, Dahlström J M, Gisselbrecht M, et al. 2011 Phys. Rev. Lett. 106 143002
Google Scholar
[4] Yang Y, Wang F, Li C G, Liu K, Tang F M, Tu Q, Zhang X F, Wang Z, Qin M Y, Liao Q 2020 Opt. Commun. 475 126221
Google Scholar
[5] Wang F, Liu K, Qin M Y, Liao Q, Lan P F, Lu P X 2019 J. Opt. Soc. Am. B 36 1829
Google Scholar
[6] Isinger M, Squibb R J, Busto D, et al. 2017 Science 358 893
Google Scholar
[7] Wang F, Liu K, Zhang X F, Wang Z, Qin M Y, Liao Q, Lu P X 2019 Phys. Rev. A 100 043405
Google Scholar
[8] Ning Q C, Peng L Y, Song S N, Jiang W C, Nagele S, Pazourek R, Burgdörfer J, Gong Q 2014 Phys. Rev. A 90 013423
Google Scholar
[9] Liao Q, Cao W, Zhang Q B, Liu K, Wang F, Lu P X, Thumm U 2020 Phys. Rev. Lett. 125 043201
Google Scholar
[10] Liao Q, Thumm U 2014 Phys. Rev. Lett. 112 023602
Google Scholar
[11] Fanciulli M, Volfová H, Muff S, Braun J, Ebert H, Minár J, Heinzmann U, Dil J H 2017 Phys. Rev. Lett. 118 067402
Google Scholar
[12] Lucchini M, Castiglioni L, Kasmi L, et al. 2015 Phys. Rev. Lett. 115 137401
Google Scholar
[13] Muller H G 1999 Laser Phys. 9 138
[14] Bauer D, Koval P 2006 Comput. Phys. Commun. 174 396
Google Scholar
[15] Madsen L B, Nikolopoulos L A A, Kjeldsen T K, Fernández J 2007 Phys. Rev. A 76 063407
Google Scholar
[16] Zhang X F, Zhu X S, Liu X, Wang F, Qin M Y, Liao Q, Lu P X 2020 Phys. Rev. A 102 033103
Google Scholar
[17] Zhang C H, Thumm U 2010 Phys. Rev. A 82 043405
Google Scholar
[18] Hermann M R, Fleck J A 1988 Phys. Rev. A 38 6000
Google Scholar
[19] Feit M D, Fleck J A, Steiger A 1982 J. Comput. Phys. 47 412
Google Scholar
[20] Dion C M, Hashemloo A, Rahali G 2014 Comput. Phys. Commun. 185 407
Google Scholar
[21] Ivanov M, Smirnova O 2011 Phys. Rev. Lett. 107 213605
Google Scholar
[22] Smirnova O, Spanner M, Ivanov M 2008 Phys. Rev. A 77 033407
Google Scholar
[23] Smirnova O, Spanner M, Ivanov M 2007 J. Phys. B 40 F197
Google Scholar
[24] Smirnova O, Spanner M, Ivanov M 2006 J. Phys. B 39 S323
Google Scholar
[25] Gersten J I, Mittleman M H 1975 Phys. Rev. A 12 1840
Google Scholar
[26] Véniard V, Taïeb R, Maquet A 1996 Phys. Rev. A 54 721
Google Scholar
[27] Toma E S, Muller H G 2002 J. Phys. B 35 3435
Google Scholar
[28] 唐富明, 刘凯, 杨溢, 屠倩, 王凤, 王哲, 廖青 2020 69 234202
Google Scholar
Tang F M, Liu K, Yang Y, Tu Q, Wang F, Wang Z, Liao Q 2020 Acta Phys. Sin. 69 234202
Google Scholar
-
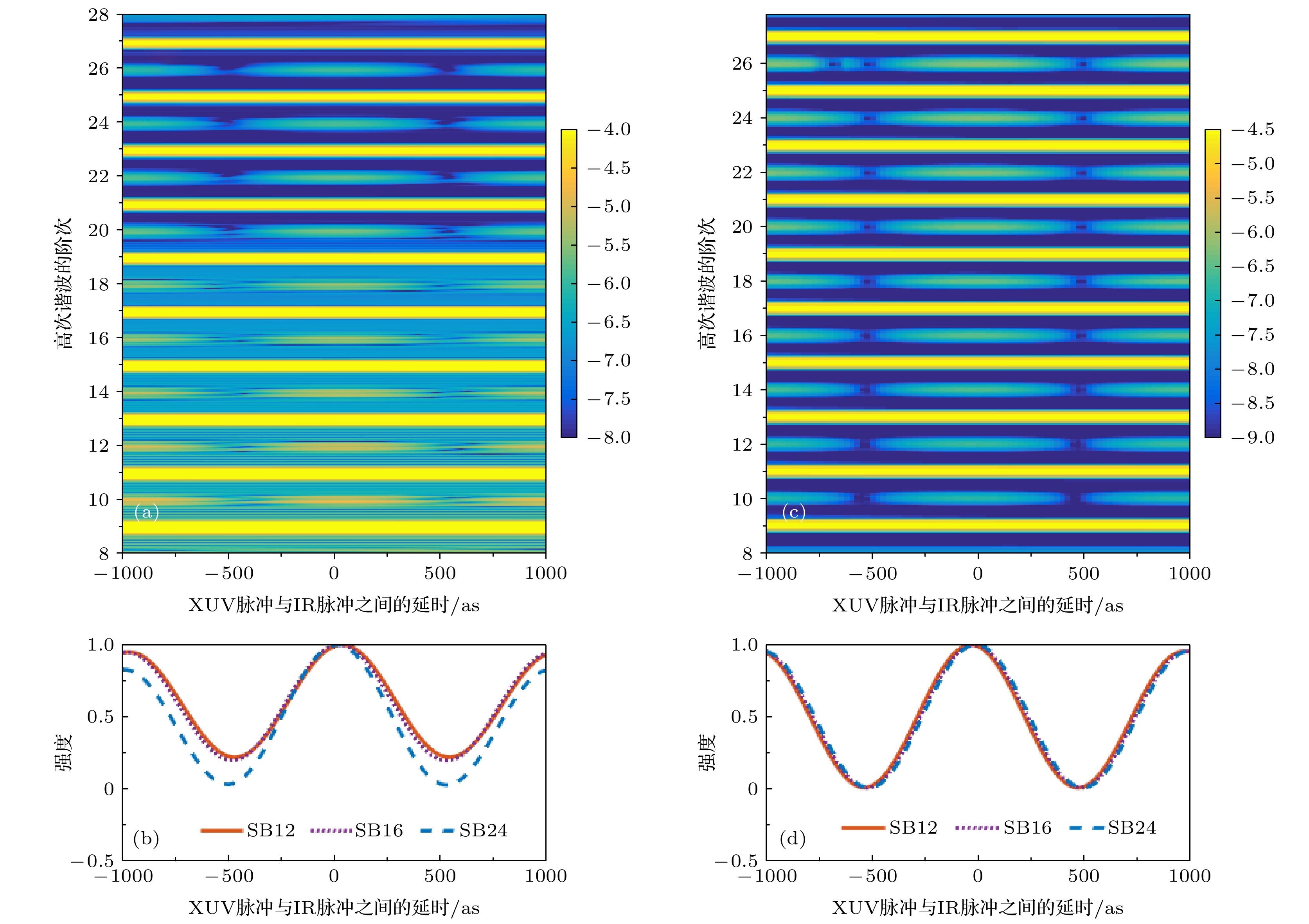
图 1 (a), (c) IR波长为600 nm时, 用TDSE和改进后EA得到的光电子能谱图, 显示了光电子跃迁几率随两个脉冲之间的延时和光电子末态动能的变化分布, 其中显示了10个主峰和9个SB; (b), (d)积分处理过的12阶, 16阶和24阶SB峰
Fig. 1. (a), (c) The photoelectron spectrograms obtained by TDSE and improved EA at the IR wavelength of 600 nm, respectively; (b), (d) the integral 12, 16 and 24 order SB peaks from (a) and (c).
图 2 TDSE(蓝色星号)、EA(红色虚线)、改进的EA(紫色虚线)和二阶微扰模型(绿色点划线)四种模型计算的不同IR波长下光电子发射时间延迟随光电子末态动能的变化 (a) λIR = 600 nm; (b) λIR = 800 nm; (c) λIR = 1200 nm; (d) λIR = 1600 nm
Fig. 2. The photoemission time delays calculated by TDSE (blue stars), EA (red dotted line), improved EA (purple dotted line) and second order perturbation model (green dotted line) with the IR wavelengths of (a) λIR = 600 nm, (b) λIR = 800 nm, (c) λIR = 1200 nm, (d) λIR = 1600 nm.
图 3 不同IR波长下光电子发射时间延迟随光电子末态动能的变化 (a) TDSE结果; (b)改进后EA结果
Fig. 3. The photoemission time delays calculated by TDSE and improved EA with different IR wavelengths: (a) TDSE; (b) the improved EA models.
-
[1] Paul P M, Toma E S, Breger P, Mullot G, Auge F, Balcou Ph, Muller H G, Agostini P 2001 Science 292 1689
Google Scholar
[2] Muller H G 2002 Appl. Phys. B 74 s17
Google Scholar
[3] Klünder K, Dahlström J M, Gisselbrecht M, et al. 2011 Phys. Rev. Lett. 106 143002
Google Scholar
[4] Yang Y, Wang F, Li C G, Liu K, Tang F M, Tu Q, Zhang X F, Wang Z, Qin M Y, Liao Q 2020 Opt. Commun. 475 126221
Google Scholar
[5] Wang F, Liu K, Qin M Y, Liao Q, Lan P F, Lu P X 2019 J. Opt. Soc. Am. B 36 1829
Google Scholar
[6] Isinger M, Squibb R J, Busto D, et al. 2017 Science 358 893
Google Scholar
[7] Wang F, Liu K, Zhang X F, Wang Z, Qin M Y, Liao Q, Lu P X 2019 Phys. Rev. A 100 043405
Google Scholar
[8] Ning Q C, Peng L Y, Song S N, Jiang W C, Nagele S, Pazourek R, Burgdörfer J, Gong Q 2014 Phys. Rev. A 90 013423
Google Scholar
[9] Liao Q, Cao W, Zhang Q B, Liu K, Wang F, Lu P X, Thumm U 2020 Phys. Rev. Lett. 125 043201
Google Scholar
[10] Liao Q, Thumm U 2014 Phys. Rev. Lett. 112 023602
Google Scholar
[11] Fanciulli M, Volfová H, Muff S, Braun J, Ebert H, Minár J, Heinzmann U, Dil J H 2017 Phys. Rev. Lett. 118 067402
Google Scholar
[12] Lucchini M, Castiglioni L, Kasmi L, et al. 2015 Phys. Rev. Lett. 115 137401
Google Scholar
[13] Muller H G 1999 Laser Phys. 9 138
[14] Bauer D, Koval P 2006 Comput. Phys. Commun. 174 396
Google Scholar
[15] Madsen L B, Nikolopoulos L A A, Kjeldsen T K, Fernández J 2007 Phys. Rev. A 76 063407
Google Scholar
[16] Zhang X F, Zhu X S, Liu X, Wang F, Qin M Y, Liao Q, Lu P X 2020 Phys. Rev. A 102 033103
Google Scholar
[17] Zhang C H, Thumm U 2010 Phys. Rev. A 82 043405
Google Scholar
[18] Hermann M R, Fleck J A 1988 Phys. Rev. A 38 6000
Google Scholar
[19] Feit M D, Fleck J A, Steiger A 1982 J. Comput. Phys. 47 412
Google Scholar
[20] Dion C M, Hashemloo A, Rahali G 2014 Comput. Phys. Commun. 185 407
Google Scholar
[21] Ivanov M, Smirnova O 2011 Phys. Rev. Lett. 107 213605
Google Scholar
[22] Smirnova O, Spanner M, Ivanov M 2008 Phys. Rev. A 77 033407
Google Scholar
[23] Smirnova O, Spanner M, Ivanov M 2007 J. Phys. B 40 F197
Google Scholar
[24] Smirnova O, Spanner M, Ivanov M 2006 J. Phys. B 39 S323
Google Scholar
[25] Gersten J I, Mittleman M H 1975 Phys. Rev. A 12 1840
Google Scholar
[26] Véniard V, Taïeb R, Maquet A 1996 Phys. Rev. A 54 721
Google Scholar
[27] Toma E S, Muller H G 2002 J. Phys. B 35 3435
Google Scholar
[28] 唐富明, 刘凯, 杨溢, 屠倩, 王凤, 王哲, 廖青 2020 69 234202
Google Scholar
Tang F M, Liu K, Yang Y, Tu Q, Wang F, Wang Z, Liao Q 2020 Acta Phys. Sin. 69 234202
Google Scholar
下载:
计量
- 文章访问数: 3969
- PDF下载量: 75
- 被引次数: 0
