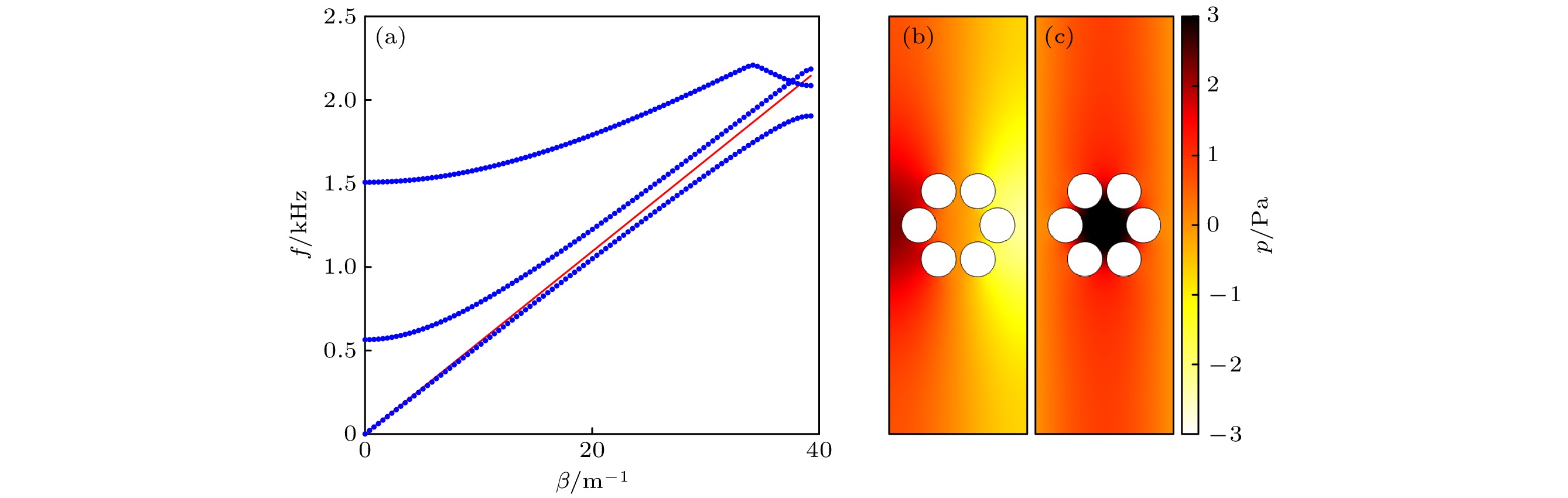
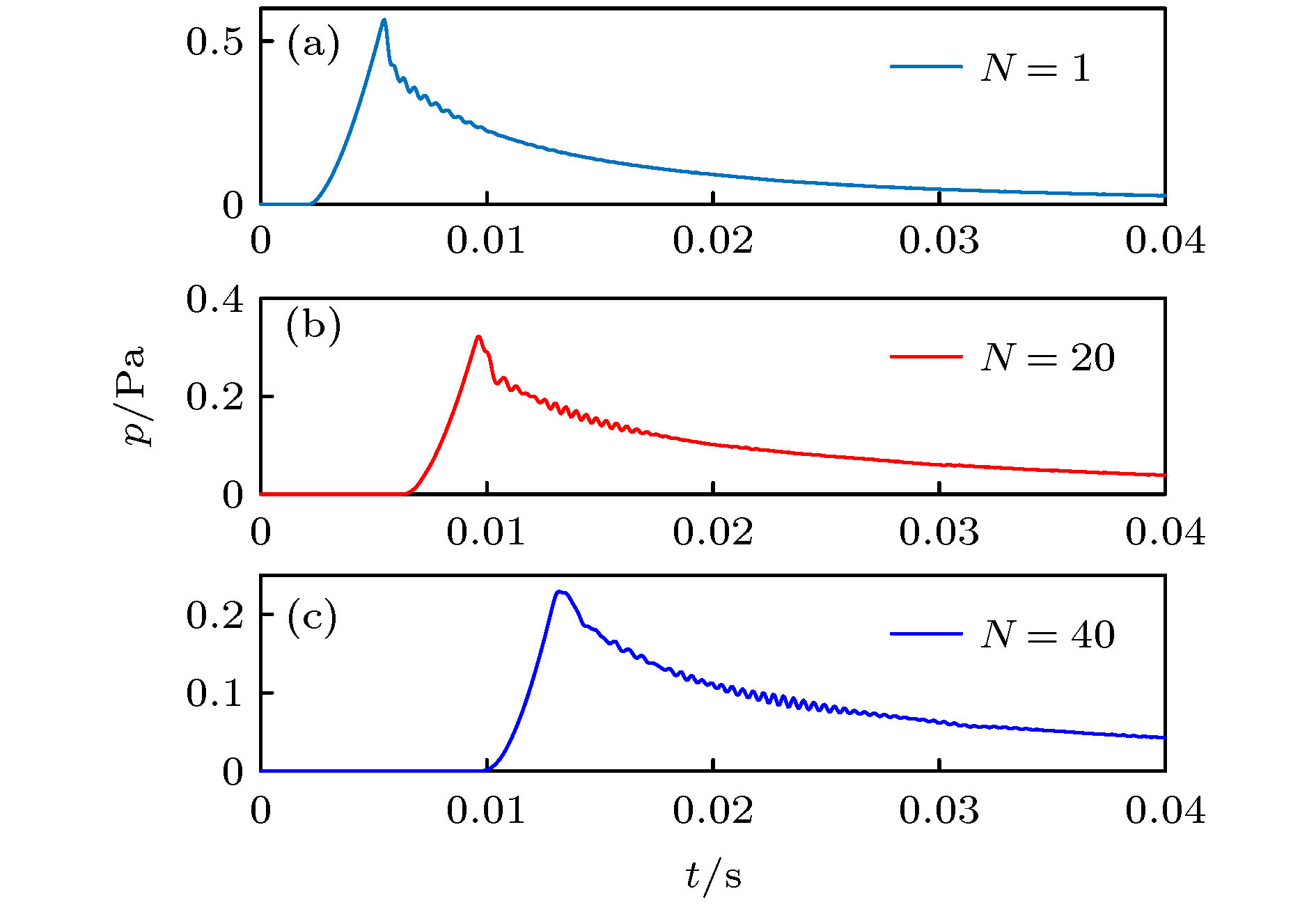
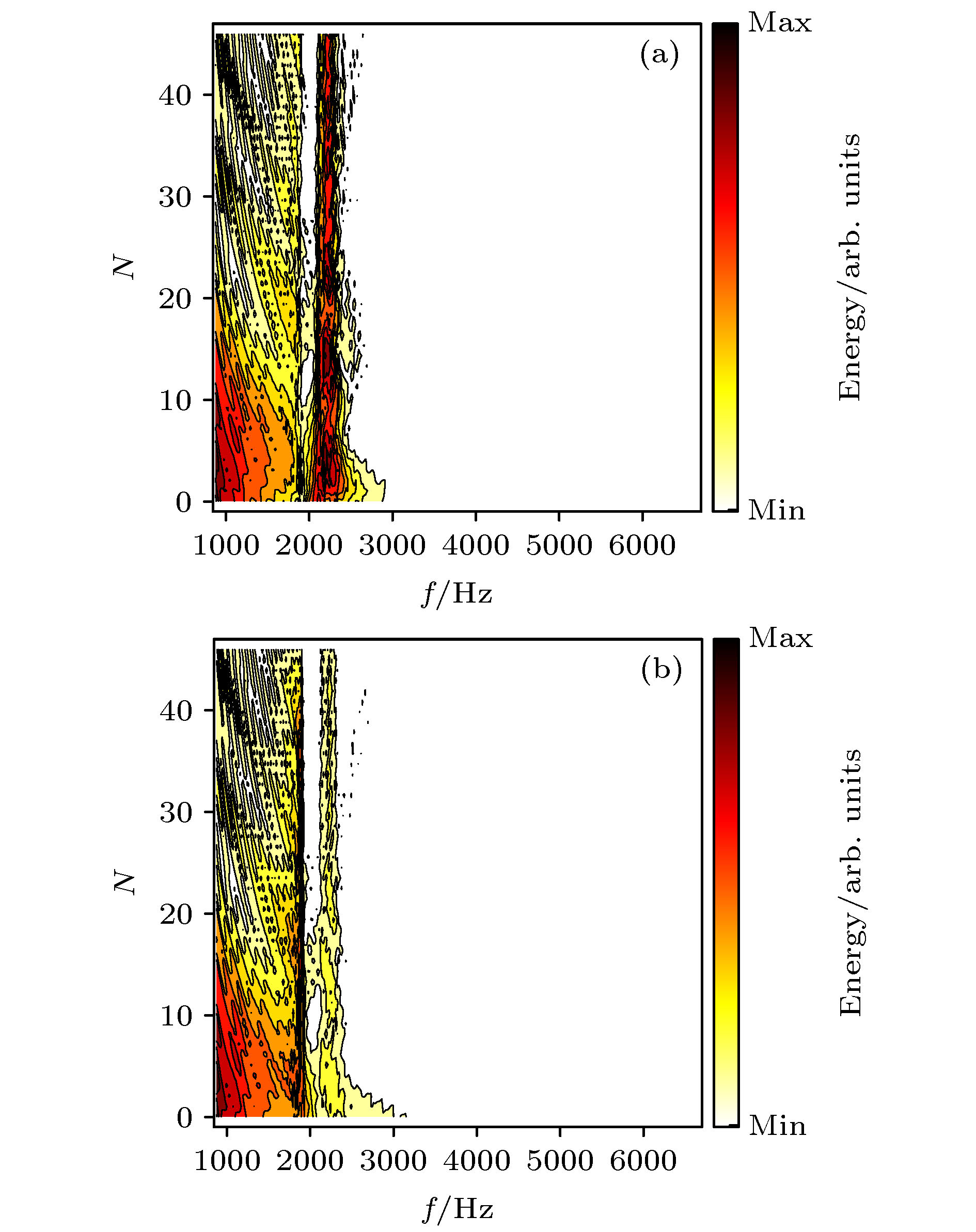
-
基于一维声栅中的Rayleigh-Bloch (RB)模式基本特点, 设计了一种单层结构弯曲声波导. 利用有限元方法从时域和频域两方面验证了弯曲声波导的有效性, RB模式波可以沿着波导的弯曲界面传播. 研究发现, 由于采用了环形结构基本单元, 在该波导中存在两种传播模式, 分别对应能量局域在单元间(模式-1)和单元内部(模式-2)两种情况. 其中, 模式-2声传输效果更佳, 几乎可实现无损传输. 时域研究中分别采用了调制脉冲和高斯脉冲两种信号形式, 分析了它们在弯曲声波导中的传输过程. 由于波导中只允许RB模式波传播, 因此对于宽频信号来说, 可起到滤波的效果. 并且, 不同模式(频率)的信号会出现在声波导的不同位置, 所得结果对于声波定向传输、声探测与识别等研究具有理论与应用价值.
-
关键词:
- Rayleigh-Bloch模式 /
- 弯曲声波导 /
- 无损传输 /
- 声探测
A monolayer bend waveguide is designed based on the features of Rayleigh-Bloch (RB) mode wave in one-dimensional diffraction grating. The feasibility that the RB mode wave can transmit along the bend waveguide is demonstrated by the time-domain and frequency-domain finite element method, respectively. The results show that two different modes of transmission wave exist because of employing the circled unit cells. They possess different acoustical energy localization positions. In mode-1, the energy is localized between unit cells. In mode-2, the energy is localized in the center of unit cell, therefore, acoustic wave transmits with nearly no loss. Modulated sinusoidal wave and Gaussian pulse wave are used in the time-domain investigation. Because only RB mode waves can transmit and different modes have different energy distributions, the bend waveguide acts as an acoustic filter for the broadband waves. This study is conducive to the acoustic wave directional transmission, acoustic signal detection and identification.-
Keywords:
- Rayleigh-Bloch mode wave /
- bend waveguide /
- no-loss transmission /
- acoustic detection
[1] Khelif A, Choujaa A, Benchabane S, Djafari-Rouhani B, Laude V 2004 Appl. Phys. Lett. 84 4400
Google Scholar
[2] Wu L Y, Chiang R Y, Tsai C N, Wu M L, Chen L W 2012 Appl. Phys. A 109 523
Google Scholar
[3] Liu F M, Huang X Q, Chang C T 2012 Appl. Phys. Lett. 100 071911
Google Scholar
[4] 王一鹤, 张志旺, 程营, 刘晓峻 2019 68 227805
Google Scholar
Wang Y H, Zhang Z W, Cheng Y, Liu X J 2019 Acta Phys. Sin. 68 227805
Google Scholar
[5] Gulyaev Y V, Plesski V P 1989 Sov. Phys. Usp. 32 51
Google Scholar
[6] Evans D V, Porter R 1999 J. Engine Math. 35 149
Google Scholar
[7] Thompson I, Linton C M 2010 SIAM J. Appl. Math. 70 2975
Google Scholar
[8] Evans D V, Porter R 2002 Q. J. Mech. Appl. Math. 55 481
Google Scholar
[9] Linton C M, McIver M 2002 J. Fluid Mech. 470 85
Google Scholar
[10] Bennetts L G, Peter M A, Montiel F 2017 J. Fluid Mech. 813 508
Google Scholar
[11] Evans D V, Linton C M 1993 Q. J. Mech. Appl. Math. 46 643
Google Scholar
[12] Atalar A, Koymen H, Oguz H K 2014 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 61 2139
Google Scholar
[13] Colquitt D J, Craster R V, Antonakakis T, Guenneau S 2015 Proc. R. Soc. London, Ser. A 471 20140465
Google Scholar
[14] Hurd R A 1954 Can. J. Phys. 32 727
Google Scholar
[15] Li C H, Ke M Z, Zhang S W, Peng S S, Qiu C Y, Liu Z Y 2016 J. Phys. D: Appl. Phys. 49 125304
Google Scholar
[16] Zhao D G, Liu Z Y, Qiu C Y, He Z J, Cai F Y, Ke M Z 2007 Phys. Rev. B 76 144301
Google Scholar
[17] Chaplain G J, Makwana M P, Craster R V 2019 Wave Motion 86 162
Google Scholar
[18] Perter M A, Meylan M H 2007 J. Fluid Mech. 575 473
Google Scholar
[19] Porter R, Evans D V 2005 Wave Motion 43 29
Google Scholar
[20] Berry M V 1975 J. Phys. A: Math. Gen. 8 1952
Google Scholar
[21] Boutin C, Rallu A, Hans S 2014 J. Mech. Phys. Solids 70 362
Google Scholar
[22] Antonakakis T, Craster R V 2012 Proc. R. Soc. London, Ser. A 468 1408
Google Scholar
[23] Craster R V, Kaplunov J, Pichugin A V 2010 Proc. R. Soc. London, Ser. A 466 2341
Google Scholar
[24] Peng Y G, Qin C Z, Zhao D G, Shen Y X, Xu X Y, Bao M, Jia H, Zhu X F 2016 Nat. Commun. 7 13368
Google Scholar
[25] Peng Y G, Shen Y X, Zhao D G, Zhu X F 2017 Appl. Phys. Lett. 110 173505
Google Scholar
[26] Peng Y G, Shen Y X, Geng Z G, Li P Q, Zhu J, Zhu X F 2020 Sci. Bull. 65 1022
Google Scholar
-
图 2 RB模式波矢图(a)及声压分布(b), (c)
Fig. 2. Band structure of the scattering cluster (a) and acoustic pressure distributions (b), (c) of RB mode waves.
图 3 散射体簇单元间(a)和单元内部(b)不同位置频谱分布
Fig. 3. Frequency spectra of the points between (a) and in (b) the scattering clusters.
图 4 弯曲波导中的RB模式声场(插图为相应波导局部声场分布结果) (a), (b)声压级分布; (c), (d)声压分布
Fig. 4. RB mode acoustic wave fields in the bend waveguide: (a), (b) Sound pressure level (SPL) distributions; (c), (d) acoustic pressure distributions. The sub-pictures are local acoustic field distributions of corresponding gratings.
图 5 不同模式下单元间(a)和单元内部(b)声压分布曲线
Fig. 5. Acoustic pressure curves for the points between (a) and in (b) the cluster under different modes.
图 6 (a)−(d)各单元内部点声压时域信号((a)所有时域信号结果; (b)−(d)第1, 20和40号单元时域信号结果)及(e)传输效率
Fig. 6. (a)−(d) Time-domain signals ((a) all of the signals; (b)−(d) three signals at unit 1, 20 and 40, respectively) and (e) transmission efficiency for the points in the cluster.
图 9 高斯脉冲入射时单元内部(a)与单元间(b)信号频谱
Fig. 9. Frequency spectra in (a) and between (b) the clusters using Gaussian pulse incidence
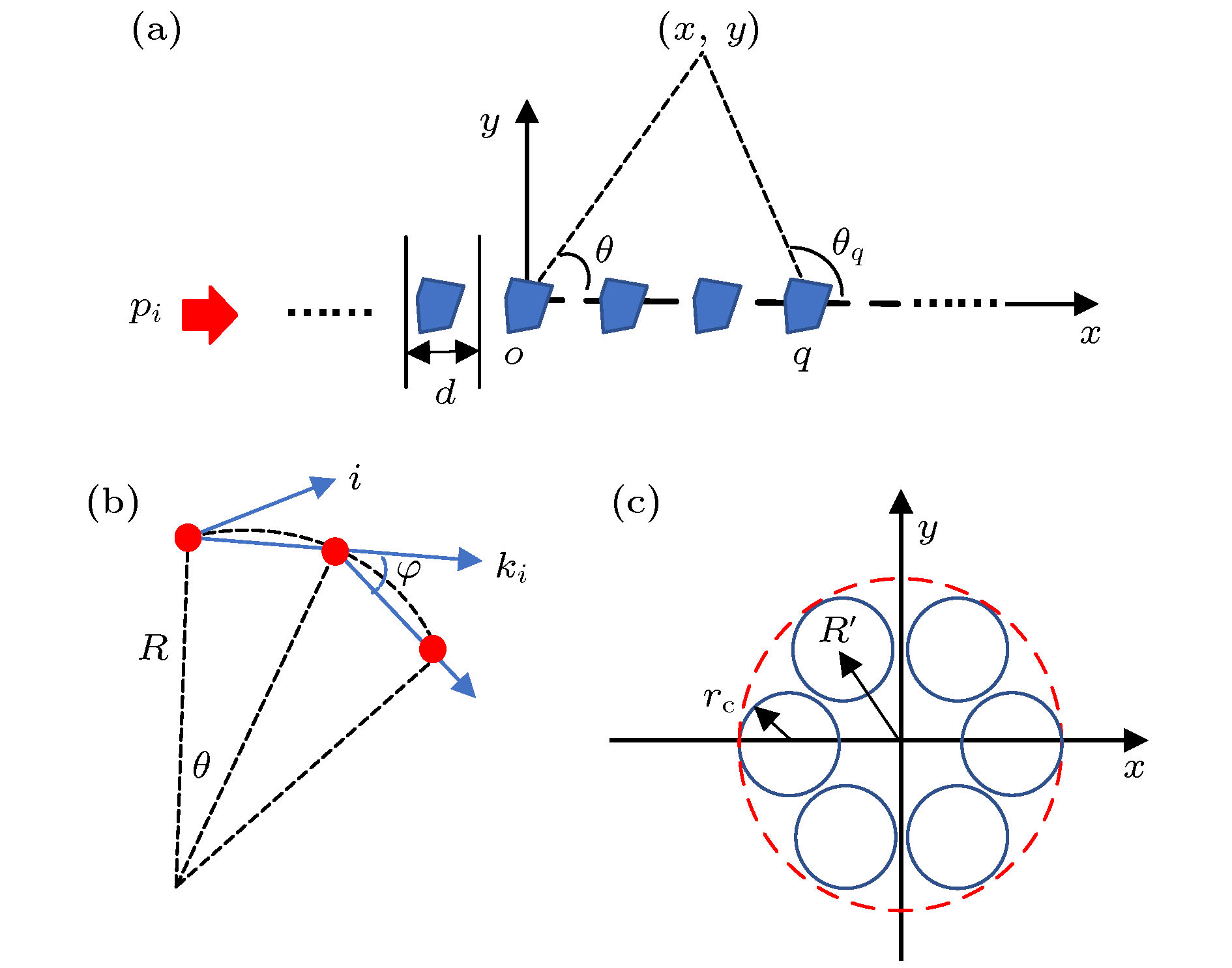
表 1 散射体簇几何参数(单位: mm)
Table 1. Geometrical parameters of the scattering cluster (Unit: mm).
rc R' R θ 单元个数N 10 22.5 2700/π π/90 46 
下载: 导出CSV
-
[1] Khelif A, Choujaa A, Benchabane S, Djafari-Rouhani B, Laude V 2004 Appl. Phys. Lett. 84 4400
Google Scholar
[2] Wu L Y, Chiang R Y, Tsai C N, Wu M L, Chen L W 2012 Appl. Phys. A 109 523
Google Scholar
[3] Liu F M, Huang X Q, Chang C T 2012 Appl. Phys. Lett. 100 071911
Google Scholar
[4] 王一鹤, 张志旺, 程营, 刘晓峻 2019 68 227805
Google Scholar
Wang Y H, Zhang Z W, Cheng Y, Liu X J 2019 Acta Phys. Sin. 68 227805
Google Scholar
[5] Gulyaev Y V, Plesski V P 1989 Sov. Phys. Usp. 32 51
Google Scholar
[6] Evans D V, Porter R 1999 J. Engine Math. 35 149
Google Scholar
[7] Thompson I, Linton C M 2010 SIAM J. Appl. Math. 70 2975
Google Scholar
[8] Evans D V, Porter R 2002 Q. J. Mech. Appl. Math. 55 481
Google Scholar
[9] Linton C M, McIver M 2002 J. Fluid Mech. 470 85
Google Scholar
[10] Bennetts L G, Peter M A, Montiel F 2017 J. Fluid Mech. 813 508
Google Scholar
[11] Evans D V, Linton C M 1993 Q. J. Mech. Appl. Math. 46 643
Google Scholar
[12] Atalar A, Koymen H, Oguz H K 2014 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 61 2139
Google Scholar
[13] Colquitt D J, Craster R V, Antonakakis T, Guenneau S 2015 Proc. R. Soc. London, Ser. A 471 20140465
Google Scholar
[14] Hurd R A 1954 Can. J. Phys. 32 727
Google Scholar
[15] Li C H, Ke M Z, Zhang S W, Peng S S, Qiu C Y, Liu Z Y 2016 J. Phys. D: Appl. Phys. 49 125304
Google Scholar
[16] Zhao D G, Liu Z Y, Qiu C Y, He Z J, Cai F Y, Ke M Z 2007 Phys. Rev. B 76 144301
Google Scholar
[17] Chaplain G J, Makwana M P, Craster R V 2019 Wave Motion 86 162
Google Scholar
[18] Perter M A, Meylan M H 2007 J. Fluid Mech. 575 473
Google Scholar
[19] Porter R, Evans D V 2005 Wave Motion 43 29
Google Scholar
[20] Berry M V 1975 J. Phys. A: Math. Gen. 8 1952
Google Scholar
[21] Boutin C, Rallu A, Hans S 2014 J. Mech. Phys. Solids 70 362
Google Scholar
[22] Antonakakis T, Craster R V 2012 Proc. R. Soc. London, Ser. A 468 1408
Google Scholar
[23] Craster R V, Kaplunov J, Pichugin A V 2010 Proc. R. Soc. London, Ser. A 466 2341
Google Scholar
[24] Peng Y G, Qin C Z, Zhao D G, Shen Y X, Xu X Y, Bao M, Jia H, Zhu X F 2016 Nat. Commun. 7 13368
Google Scholar
[25] Peng Y G, Shen Y X, Zhao D G, Zhu X F 2017 Appl. Phys. Lett. 110 173505
Google Scholar
[26] Peng Y G, Shen Y X, Geng Z G, Li P Q, Zhu J, Zhu X F 2020 Sci. Bull. 65 1022
Google Scholar
下载:
计量
- 文章访问数: 5472
- PDF下载量: 75
- 被引次数: 0
