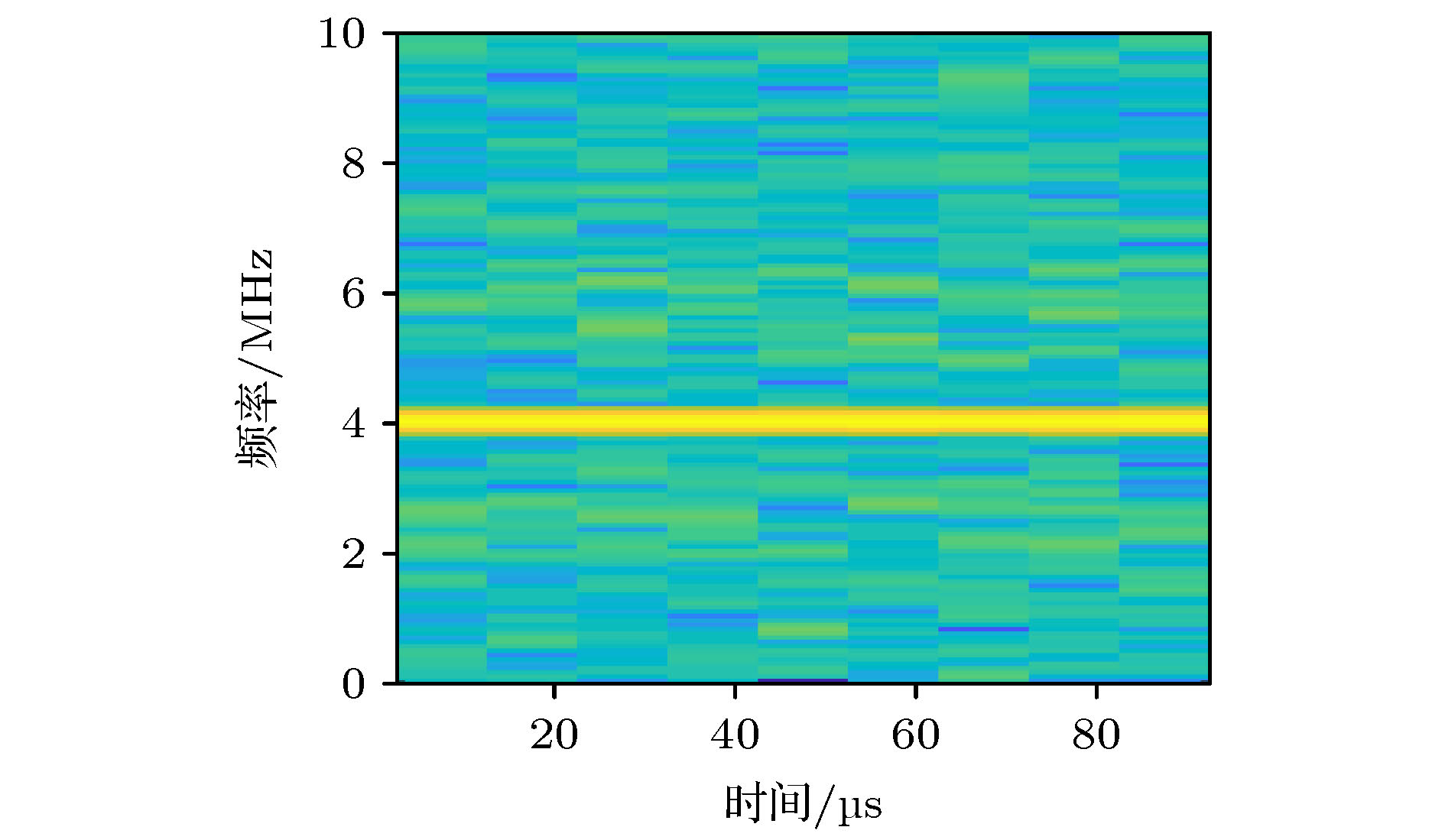
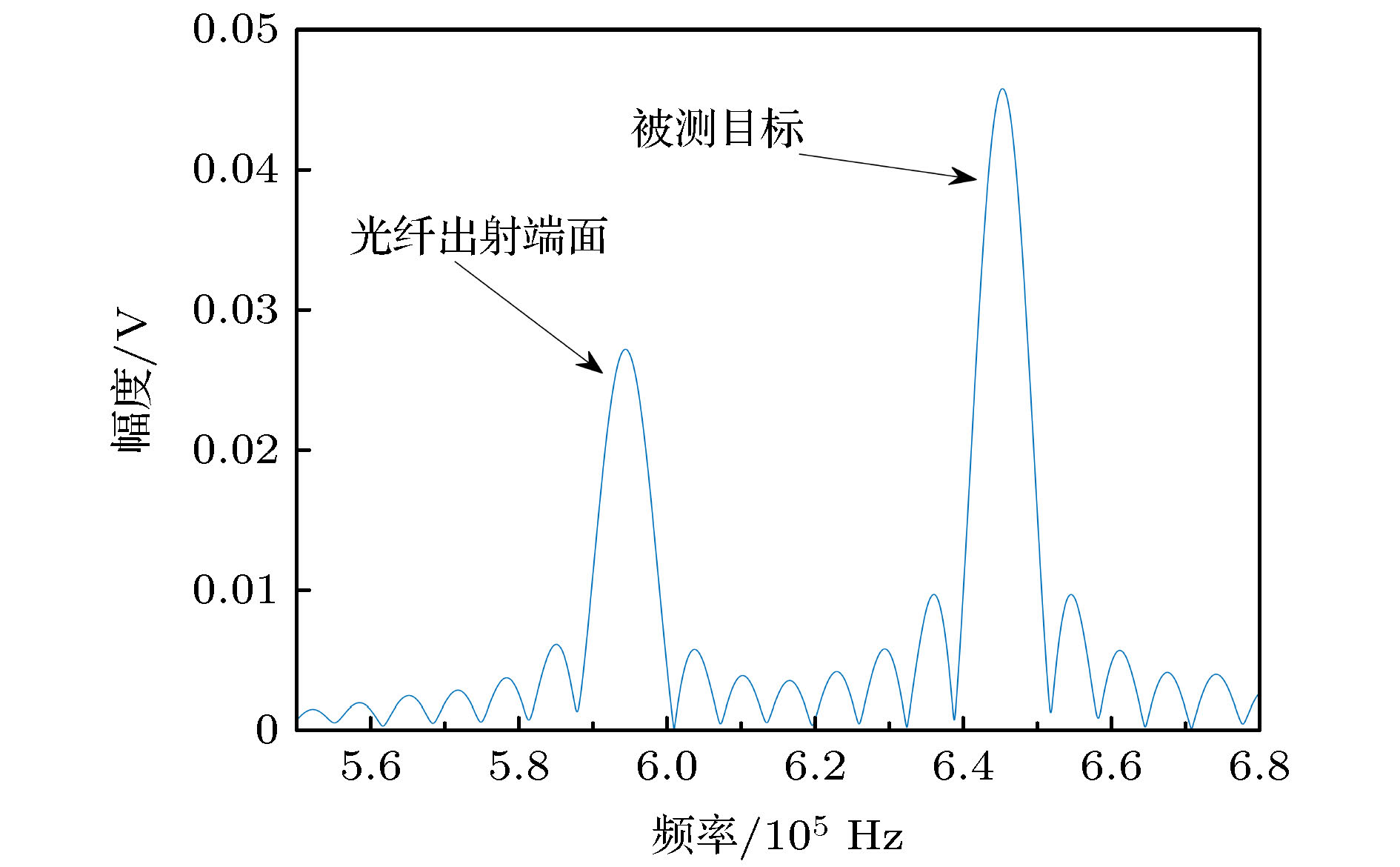
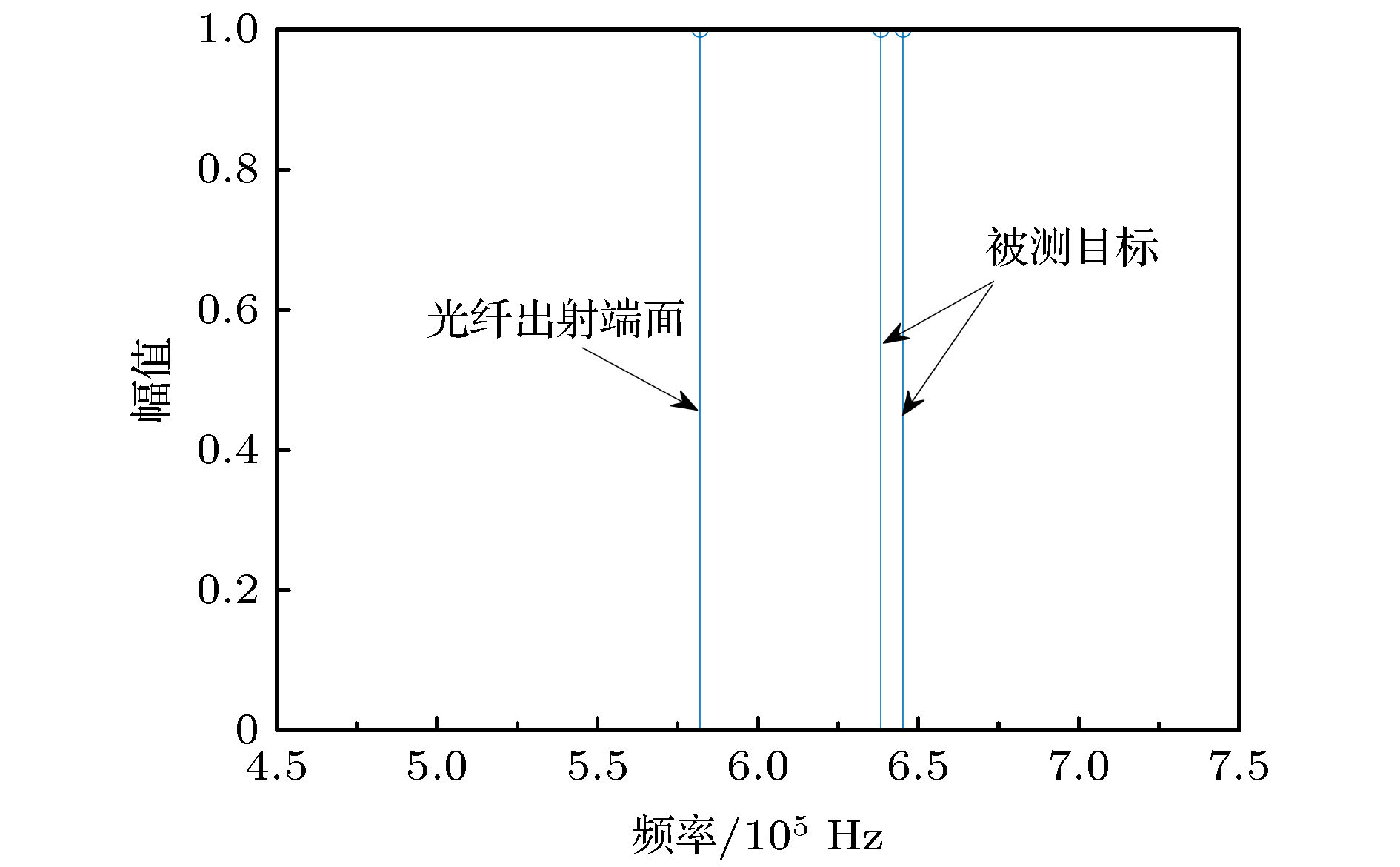
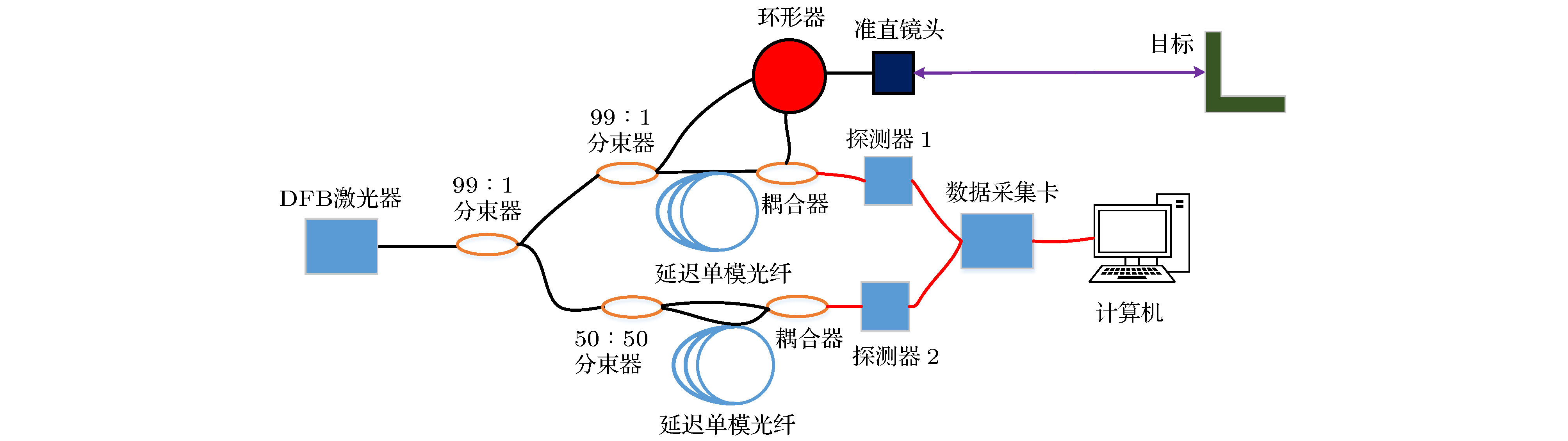
-
激光扫频干涉测量技术具有无测距盲区、非接触、单次测量多目标的能力. 通过傅里叶变换可提取目标拍频频率, 进而解算距离. 然而受激光器调频带宽限制, 通过傅里叶变换得到的目标分辨率受限于固有分辨率. 为解决该问题, 本文提出采用基于旋转不变技术的信号参数估计(ESPRIT)算法对测量信号进行频谱分析. 实验通过插值拟合法校正测量信号拍频非线性, 进而采用ESPRIT算法测量目标距离, 结果表明在傅里叶变换算法无法区分临近目标频率的情况下, 采用ESPRIT算法可以区分出目标的频率, 通过计算可得被测目标的厚度为2.08 mm. 从而为诸如光纤临近损伤点、薄台阶高度或小孔等测量提供了思路.
-
关键词:
- 激光扫频干涉测量 /
- 快速傅里叶变换 /
- 基于旋转不变技术的信号参数估计算法
The laser frequency scanning interferometry, as a non-contact method, has non-ranging blind zone and achieves multi-target testing in a single measurement. The beat frequency of target can be extracted by Fourier transform, and then the distance can be solved. However, due to the limitation of laser frequency modulation bandwidth, the resolution of target obtained by Fourier transform is limited to the inherent resolution. In order to solve this problem, in this paper we propose to use the estimating signal parameter via rotational invariance technique (ESPRIT) to perform spectrum analysis on the measured signal. In the experiment, the resampling method is adopted to correct the non-linearity of the measured signal beat frequency, and then the ESPRIT algorithm is used to obtain the target distance. The results show that the Fourier transform algorithm cannot distinguish the target signal from the frequencies of adjacent target, but the ESPRIT algorithm can do. The thickness of the measured target is 2.08 mm. This provides ideas for measuring, such as damage point in the proximity of the fiber, height of thin step, or small hole.-
Keywords:
- laser frequency scanning interferometry /
- fast Fourier transform /
- estimating signal parameter via rotational invariance technique algorithm
[1] 谭林秋, 华灯鑫, 汪丽, 高飞, 狄慧鸽 2014 63 224205
Google Scholar
Tan L Q, Hua D X, Wang L, Gao F, Di H G 2014 Acta Phys. Sin. 63 224205
Google Scholar
[2] 杨凌辉 2010 博士学位论文 (天津: 天津大学)
Yang L H 2010Ph. D. Dissertation (Tianjin: Tianjin University) (in Chinese)
[3] Yang Z D, Wang P, Li X H, Sun C K 2014 Opt. Lasers Eng. 54 31
Google Scholar
[4] 高峰, 郭为忠, 宋清玉, 杜凤山 2010 机械工程学报 46 92
Google Scholar
Gao F, Guo W Z, Song Q, Du F S 2010 Chin. J. Mech. Eng. 46 92
Google Scholar
[5] Wen X D, Ning T G, You H D, Kang Z X, Li J, Li C, Feng T, Yu S W, Jian W 2014 Chin. Phys. Lett. 31 034203
Google Scholar
[6] 刘亭洋, 张福民, 吴翰钟, 李建双, 石永强, 曲兴华 2016 66 020601
Google Scholar
Liu T Y, Zhang F M, Wu H Z, Li J S, Shi Y Q, Qu X H 2016 Acta Phys. Sin. 66 020601
Google Scholar
[7] 时光, 张福民, 曲兴华, 孟祥松 2014 63 184209
Google Scholar
Shi G, Zhang F M, Qu X H, Meng X S 2014 Acta Phys. Sin. 63 184209
Google Scholar
[8] Shi G, Wang W, Zhang F M 2018 Opt. Commun. 411 152
Google Scholar
[9] Schneider R 2001 Opt. Eng. 40 33
Google Scholar
[10] Arseny V, Naresh S, Xu S B 2010 Appl. Opt. 49 1932
Google Scholar
[11] Yu X, Hong G L, Ling Y 2011 Acta Opt. Sin. 31 0606002
Google Scholar
[12] 孟祥松, 张福民, 曲兴华 2015 64 230601
Google Scholar
Meng X S, Zhang F M, Qu X H 2015 Acta Phys. Sin. 64 230601
Google Scholar
[13] Xu S Z, Kooij B J, Yarovoy A 2019 Sig. Pro. 168 107259
[14] Sébastien L F, Yves S, Rostand M, Patrick F 2008 Appl. Opt. 47 3027
Google Scholar
[15] John D, Ben H, Andrew J L, Andrew J L, Armin J H 2014 Opt. Express 22 24869
Google Scholar
[16] Mateo A B, Barber Z W 2015 Appl. Opt. 54 6019
Google Scholar
[17] Lippok N, Coen S, Nielsen P 2012 Opt. Express 20 23398
Google Scholar
[18] Jiang S, Liu B, Wang H C, Zhao B 2019 Sensors 19 5132
Google Scholar
[19] Pan H, Zhang F M, Shi C Z, Qu X H 2017 Appl. Opt. 56 6956
Google Scholar
[20] Deng Z W, Liu Z G, Gu S W, Jia X Y, Deng W, Yan H H 2020 Opt. Commun. 455 124556
Google Scholar
[21] Deng Z W, Liu Z G, Jia X Y, Deng W, Zhang X, Wang Z Y 2019 Appl. Opt. 58 6865
Google Scholar
[22] 刘国栋, 许新科, 刘炳国, 陈凤东, 胡涛, 路程, 甘雨 2016 65 209501
Google Scholar
Liu G D, Xu X K, Liu B G, Chen F D, Hu T, Lu C, Gan Y 2016 Acta Phys. Sin. 65 209501
Google Scholar
[23] 许新科, 刘国栋, 刘炳国, 陈凤东, 庄志涛, 甘雨 2015 64 219501
Google Scholar
Xu X K, Liu G D, Liu B G, Chen F D, Zhuang Z T, Gan Y 2015 Acta Phys. Sin. 64 219501
Google Scholar
[24] 张立宏 2013 博士学位论文 (哈尔滨: 哈尔滨工业大学)
Zhang L H 2013Ph. D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
[25] 许新科 2017 博士学位论文 (哈尔滨: 哈尔滨工业大学)
Xu X K 2017 Ph. D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
-
图 1 激光扫频干涉测距系统示意图
Fig. 1. Schematic diagram of laser scanning interference ranging system.
图 2 激光拍频干涉测距原理图(PA, 检偏器)
Fig. 2. Schematic diagram of laser beat frequency interference ranging (PA, polarization analyzer).
图 3 激光扫频干涉测量拍频形成原理图
Fig. 3. Schematic diagram of beat frequency formation in laser frequency scanning interferometry.
图 4 未采用插值拟合时信号的频谱图
Fig. 4. Spectral diagram of the signal without interpolation fitting.
图 5 未采用插值拟合信号的时频图
Fig. 5. Time-frequency diagram of the signal without interpolation fitting.
图 7 采用插值拟合后信号的时频图
Fig. 7. Time-frequency diagram of the signal with interpolation fitting.
表 1 不同距离下三种算法的测量结果与实际距离的比较
Table 1. Comparison of the measurement results of three algorithms and the actual distance under different distances.
实际距
离/mmFFT算法
误差/mmMUSIC算法
误差/mmESPRIT算法
误差/mm127.633 –0.005 –0.328 0.007 100.797 –0.013 0.600 0.012 109.165 –0.010 0.230 0.009 99.154 0.003 –0.093 –0.002 124.060 –0.016 –0.621 0.014 
下载: 导出CSV
表 2 ESPRIT算法对不同厚度的双目标的测量结果与实际厚度的比较
Table 2. Comparison of the measurement results of the ESPRIT algorithm with the actual thickness of dual targets.
实际厚度/mm ESPRIT测量结果/mm 误差/mm 15.362 15.327 –0.035 20.291 20.316 0.025 24.144 24.182 0.038
下载: 导出CSV
-
[1] 谭林秋, 华灯鑫, 汪丽, 高飞, 狄慧鸽 2014 63 224205
Google Scholar
Tan L Q, Hua D X, Wang L, Gao F, Di H G 2014 Acta Phys. Sin. 63 224205
Google Scholar
[2] 杨凌辉 2010 博士学位论文 (天津: 天津大学)
Yang L H 2010Ph. D. Dissertation (Tianjin: Tianjin University) (in Chinese)
[3] Yang Z D, Wang P, Li X H, Sun C K 2014 Opt. Lasers Eng. 54 31
Google Scholar
[4] 高峰, 郭为忠, 宋清玉, 杜凤山 2010 机械工程学报 46 92
Google Scholar
Gao F, Guo W Z, Song Q, Du F S 2010 Chin. J. Mech. Eng. 46 92
Google Scholar
[5] Wen X D, Ning T G, You H D, Kang Z X, Li J, Li C, Feng T, Yu S W, Jian W 2014 Chin. Phys. Lett. 31 034203
Google Scholar
[6] 刘亭洋, 张福民, 吴翰钟, 李建双, 石永强, 曲兴华 2016 66 020601
Google Scholar
Liu T Y, Zhang F M, Wu H Z, Li J S, Shi Y Q, Qu X H 2016 Acta Phys. Sin. 66 020601
Google Scholar
[7] 时光, 张福民, 曲兴华, 孟祥松 2014 63 184209
Google Scholar
Shi G, Zhang F M, Qu X H, Meng X S 2014 Acta Phys. Sin. 63 184209
Google Scholar
[8] Shi G, Wang W, Zhang F M 2018 Opt. Commun. 411 152
Google Scholar
[9] Schneider R 2001 Opt. Eng. 40 33
Google Scholar
[10] Arseny V, Naresh S, Xu S B 2010 Appl. Opt. 49 1932
Google Scholar
[11] Yu X, Hong G L, Ling Y 2011 Acta Opt. Sin. 31 0606002
Google Scholar
[12] 孟祥松, 张福民, 曲兴华 2015 64 230601
Google Scholar
Meng X S, Zhang F M, Qu X H 2015 Acta Phys. Sin. 64 230601
Google Scholar
[13] Xu S Z, Kooij B J, Yarovoy A 2019 Sig. Pro. 168 107259
[14] Sébastien L F, Yves S, Rostand M, Patrick F 2008 Appl. Opt. 47 3027
Google Scholar
[15] John D, Ben H, Andrew J L, Andrew J L, Armin J H 2014 Opt. Express 22 24869
Google Scholar
[16] Mateo A B, Barber Z W 2015 Appl. Opt. 54 6019
Google Scholar
[17] Lippok N, Coen S, Nielsen P 2012 Opt. Express 20 23398
Google Scholar
[18] Jiang S, Liu B, Wang H C, Zhao B 2019 Sensors 19 5132
Google Scholar
[19] Pan H, Zhang F M, Shi C Z, Qu X H 2017 Appl. Opt. 56 6956
Google Scholar
[20] Deng Z W, Liu Z G, Gu S W, Jia X Y, Deng W, Yan H H 2020 Opt. Commun. 455 124556
Google Scholar
[21] Deng Z W, Liu Z G, Jia X Y, Deng W, Zhang X, Wang Z Y 2019 Appl. Opt. 58 6865
Google Scholar
[22] 刘国栋, 许新科, 刘炳国, 陈凤东, 胡涛, 路程, 甘雨 2016 65 209501
Google Scholar
Liu G D, Xu X K, Liu B G, Chen F D, Hu T, Lu C, Gan Y 2016 Acta Phys. Sin. 65 209501
Google Scholar
[23] 许新科, 刘国栋, 刘炳国, 陈凤东, 庄志涛, 甘雨 2015 64 219501
Google Scholar
Xu X K, Liu G D, Liu B G, Chen F D, Zhuang Z T, Gan Y 2015 Acta Phys. Sin. 64 219501
Google Scholar
[24] 张立宏 2013 博士学位论文 (哈尔滨: 哈尔滨工业大学)
Zhang L H 2013Ph. D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
[25] 许新科 2017 博士学位论文 (哈尔滨: 哈尔滨工业大学)
Xu X K 2017 Ph. D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
下载:
计量
- 文章访问数: 5984
- PDF下载量: 79
- 被引次数: 0
