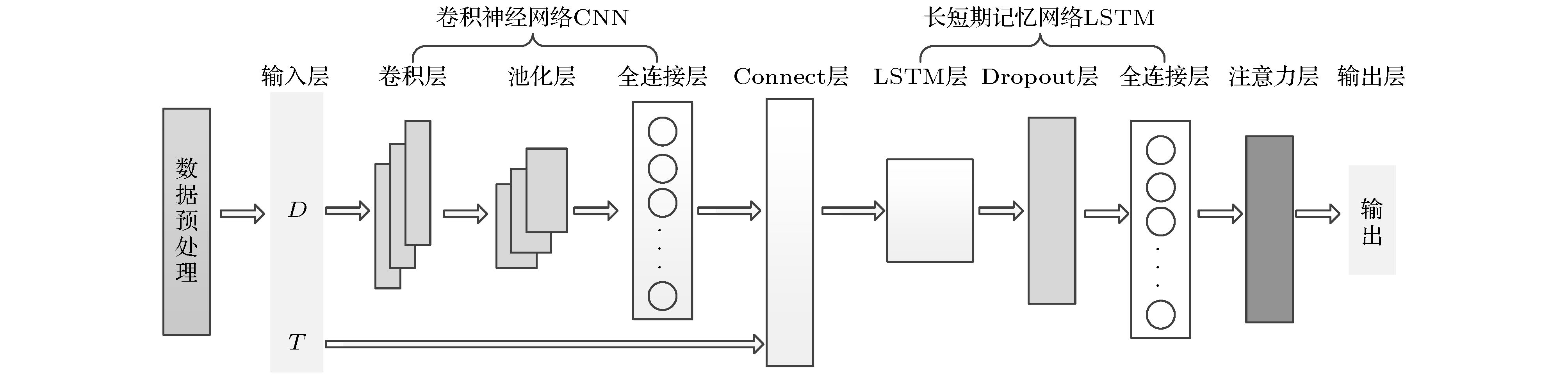
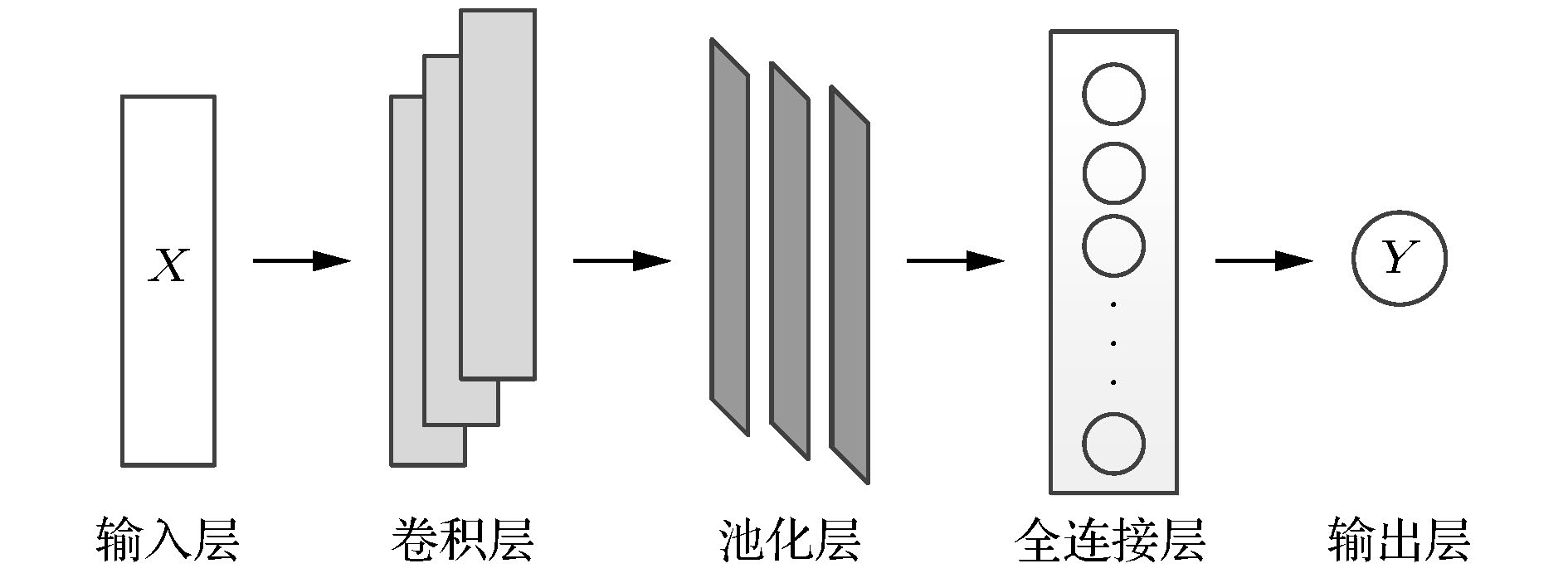
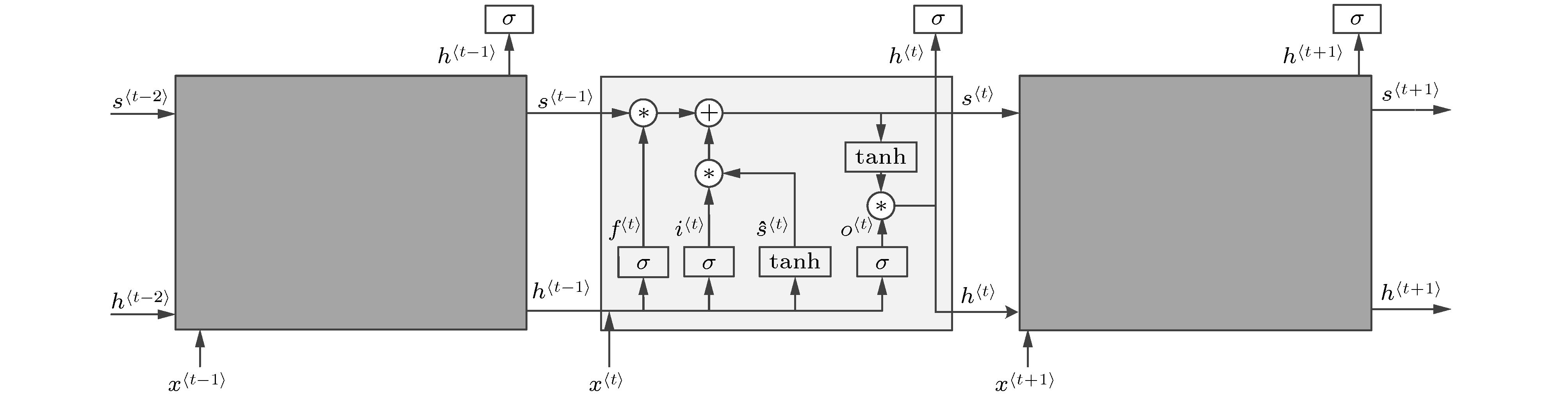
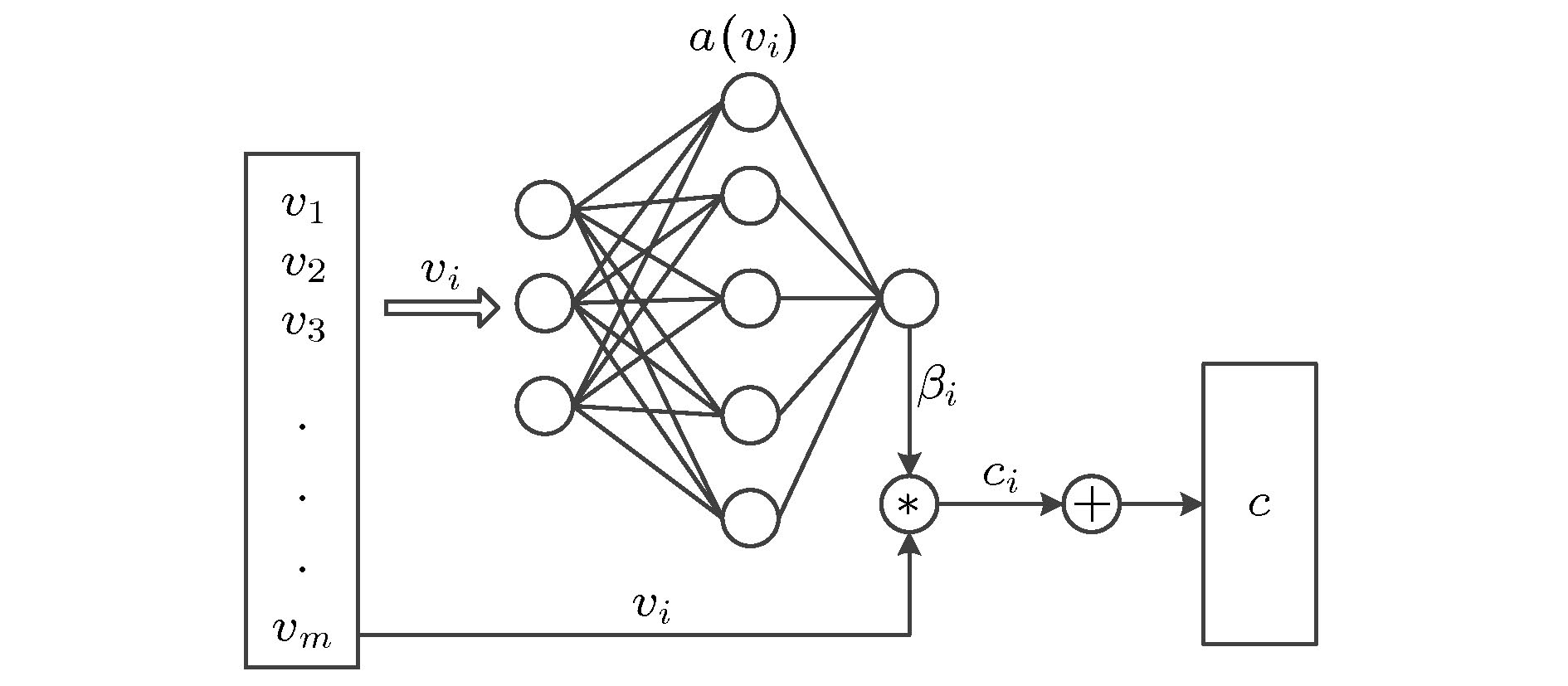
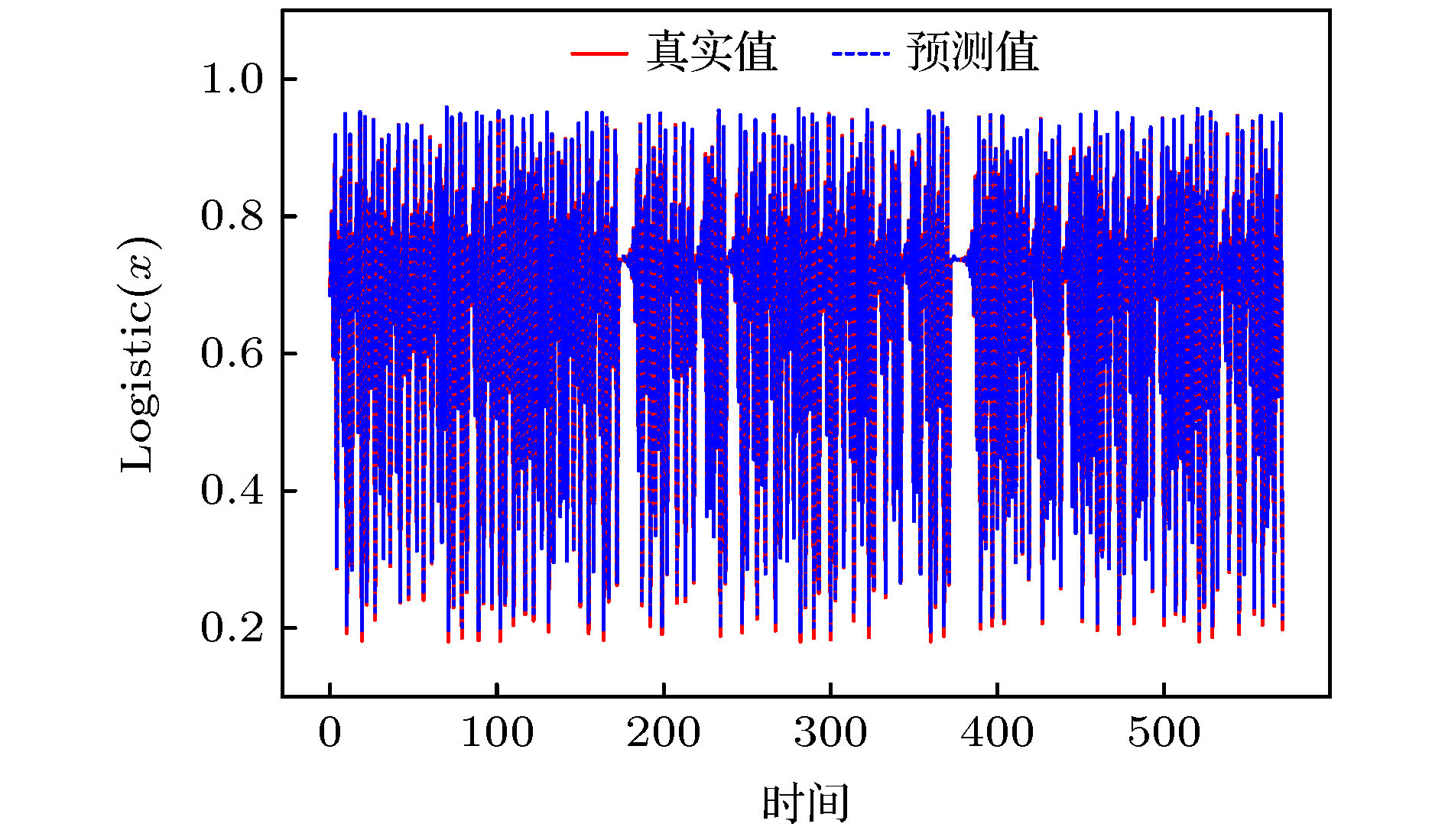
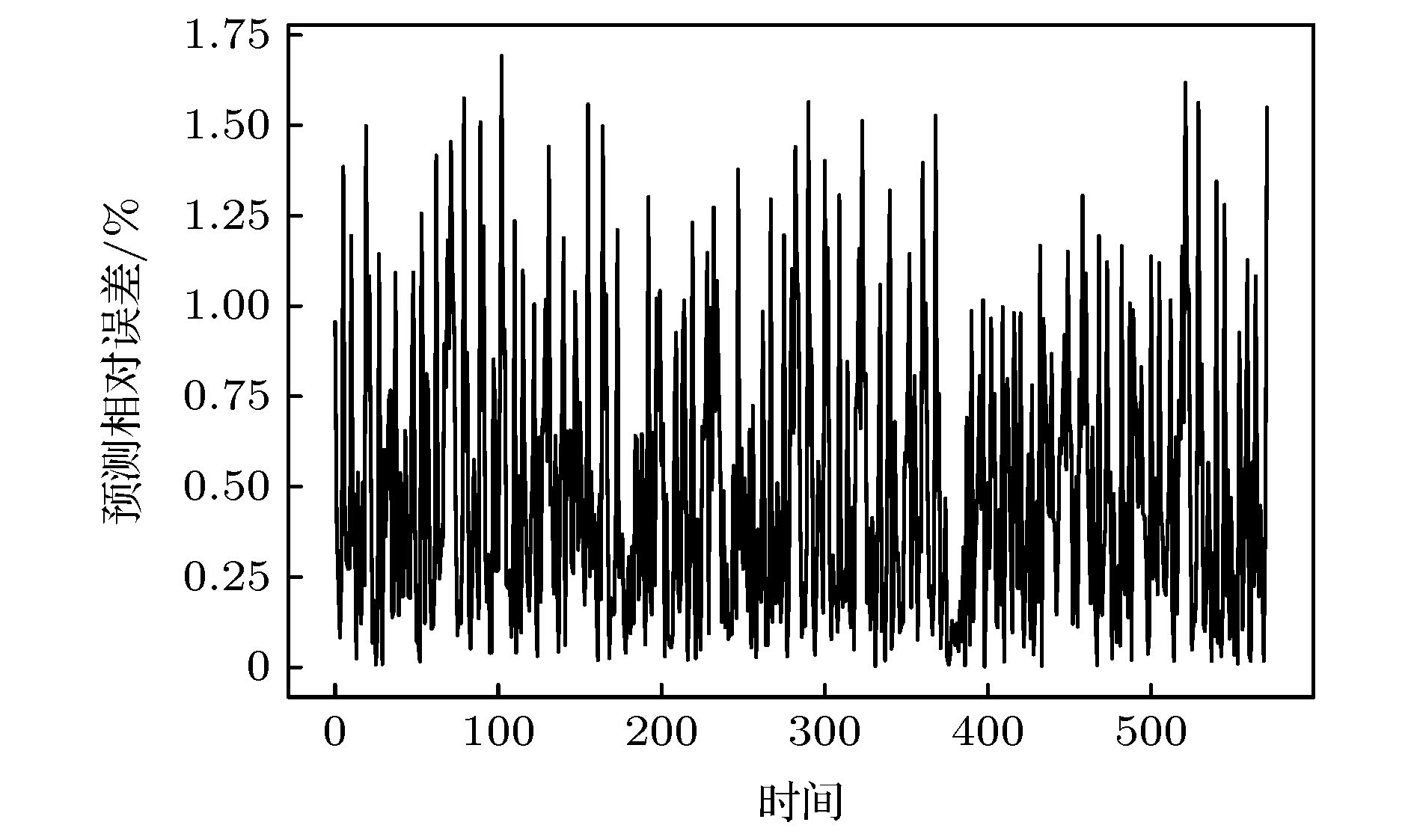
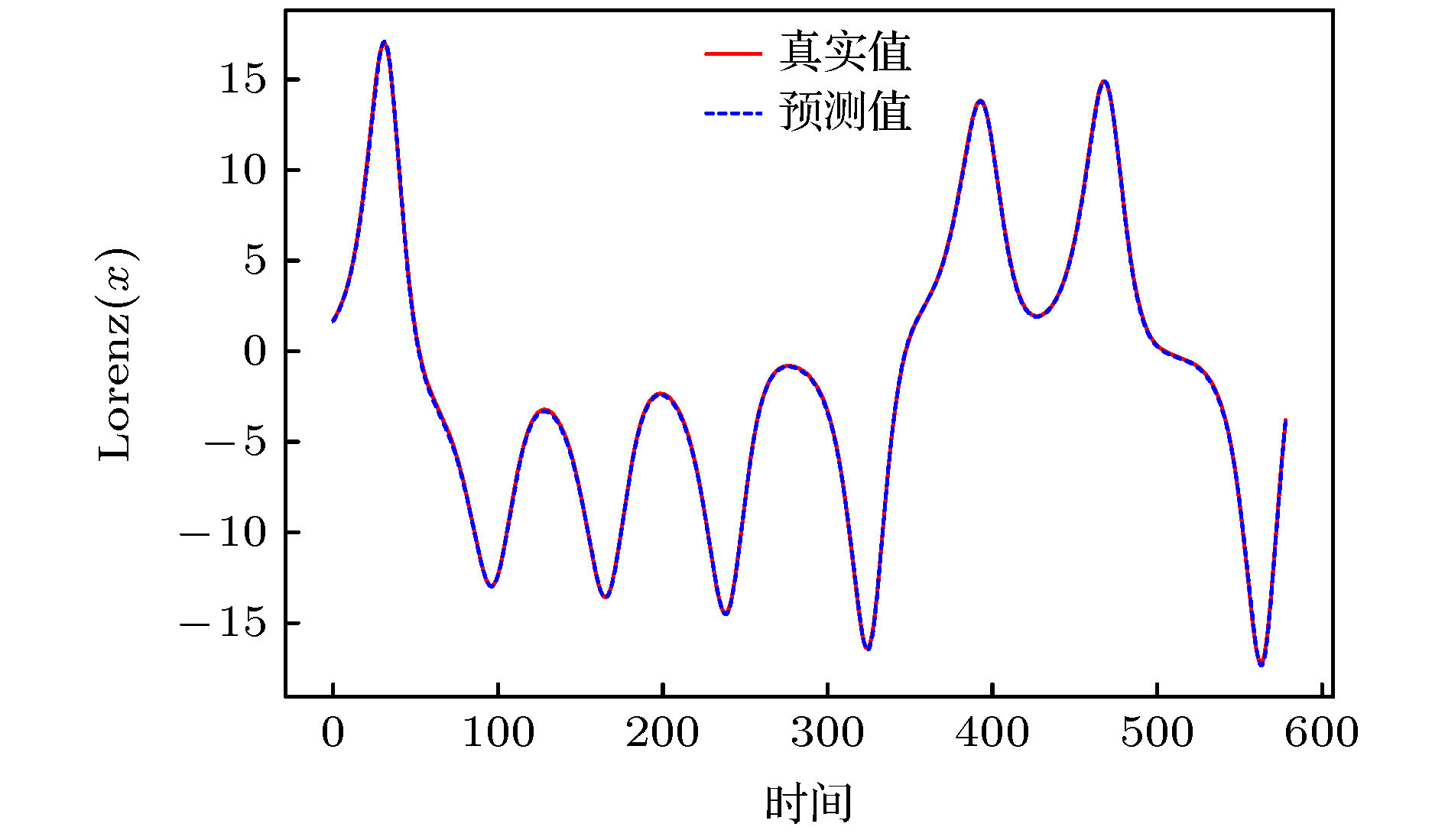
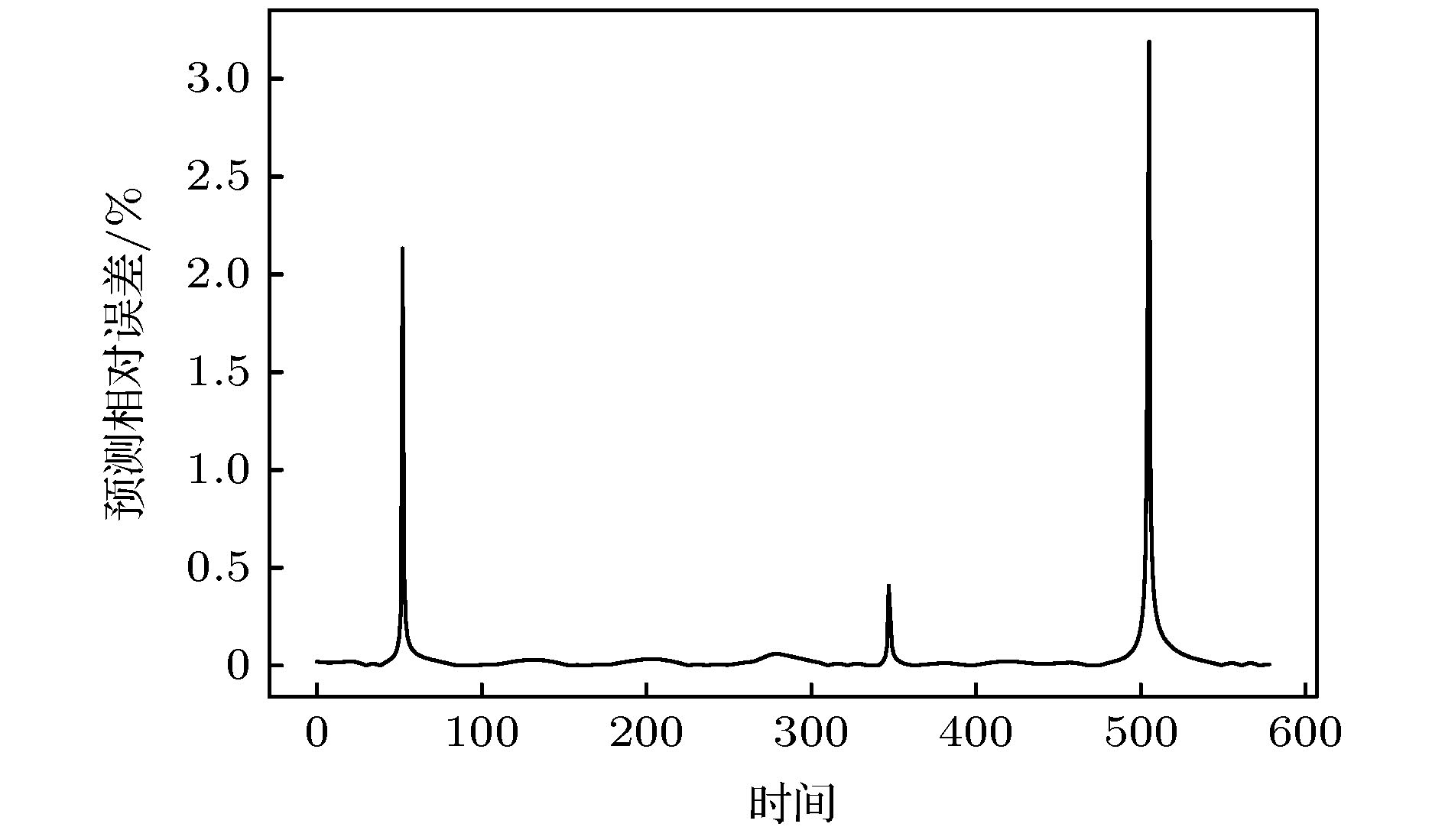
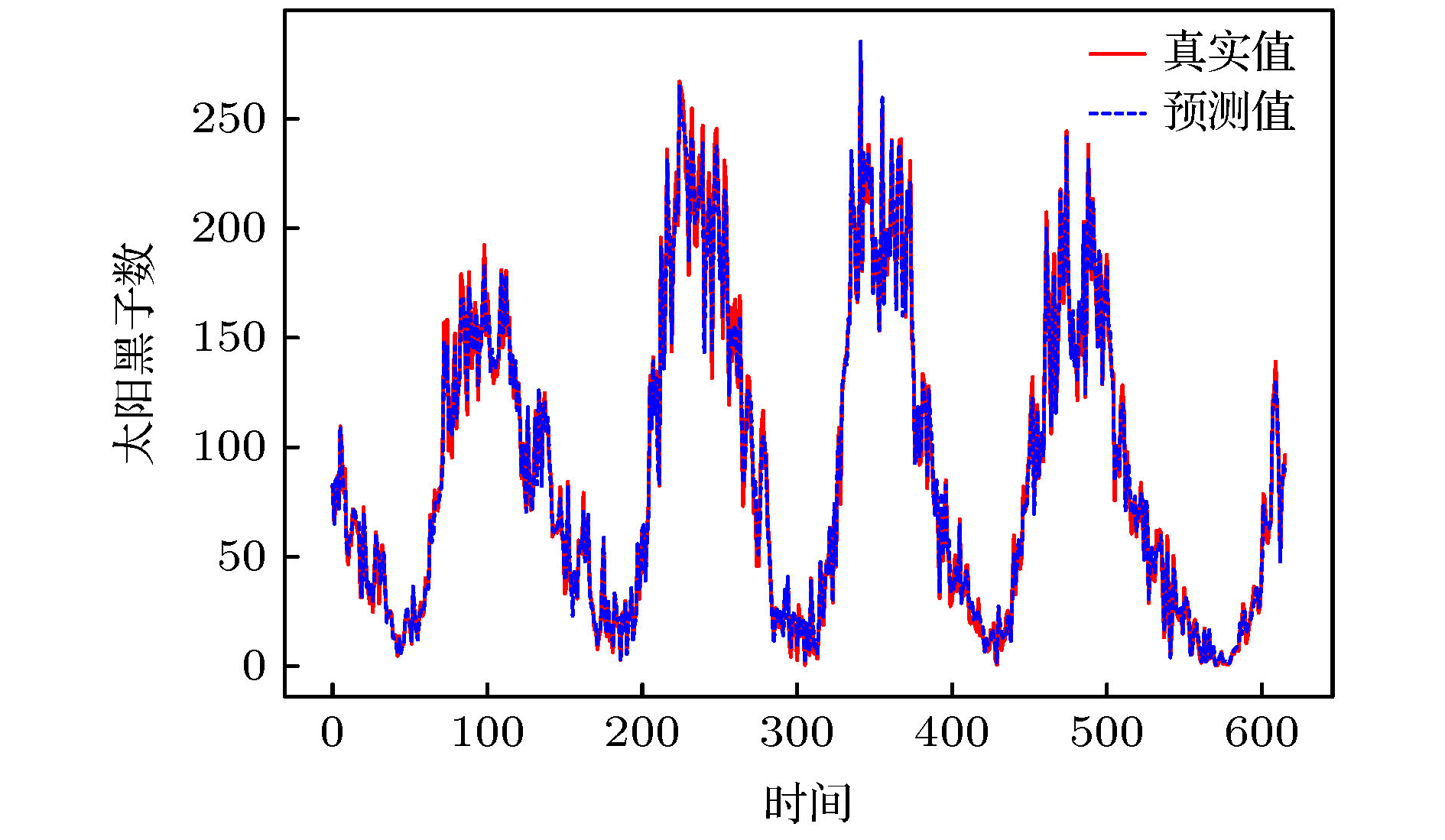
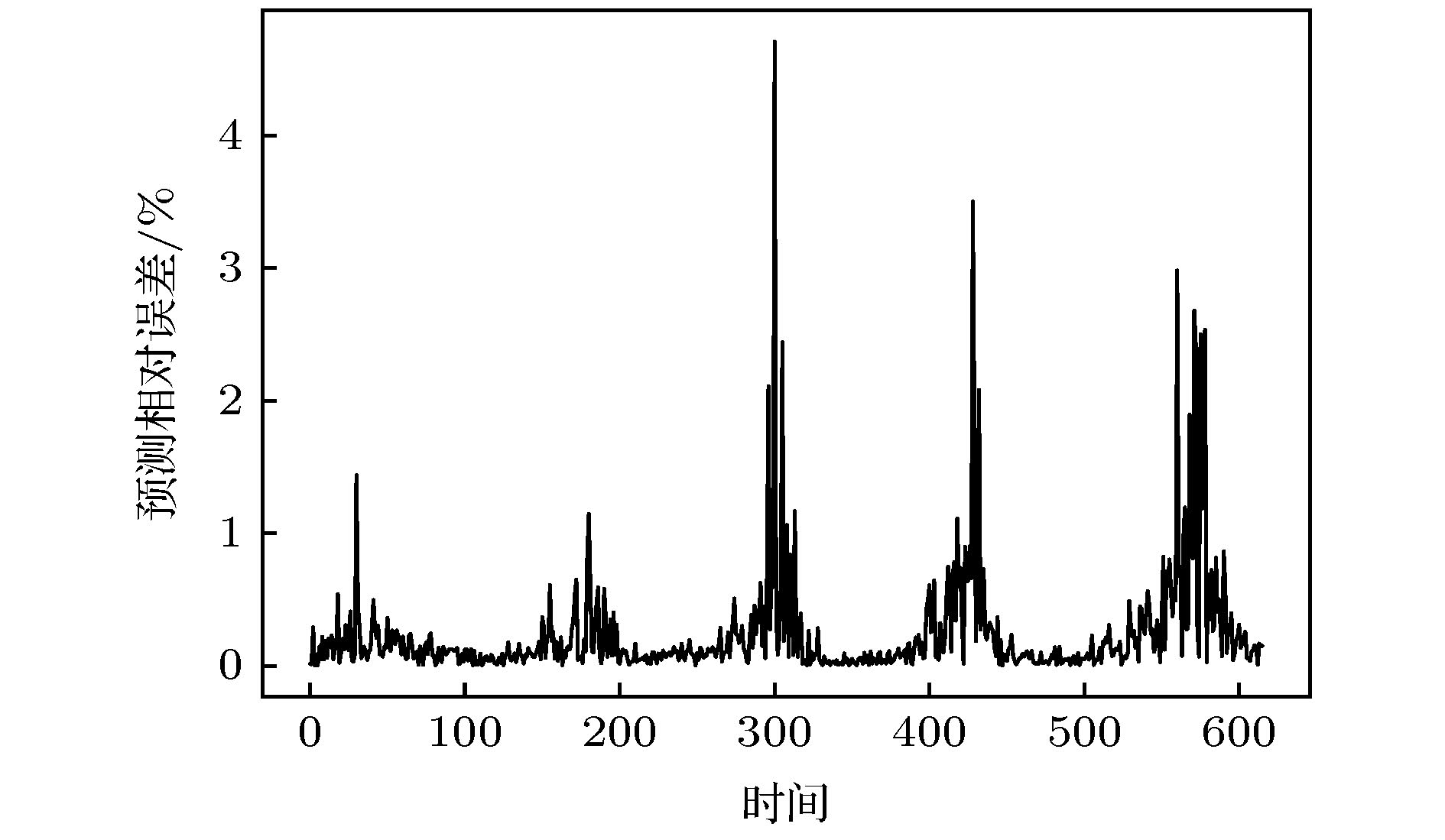
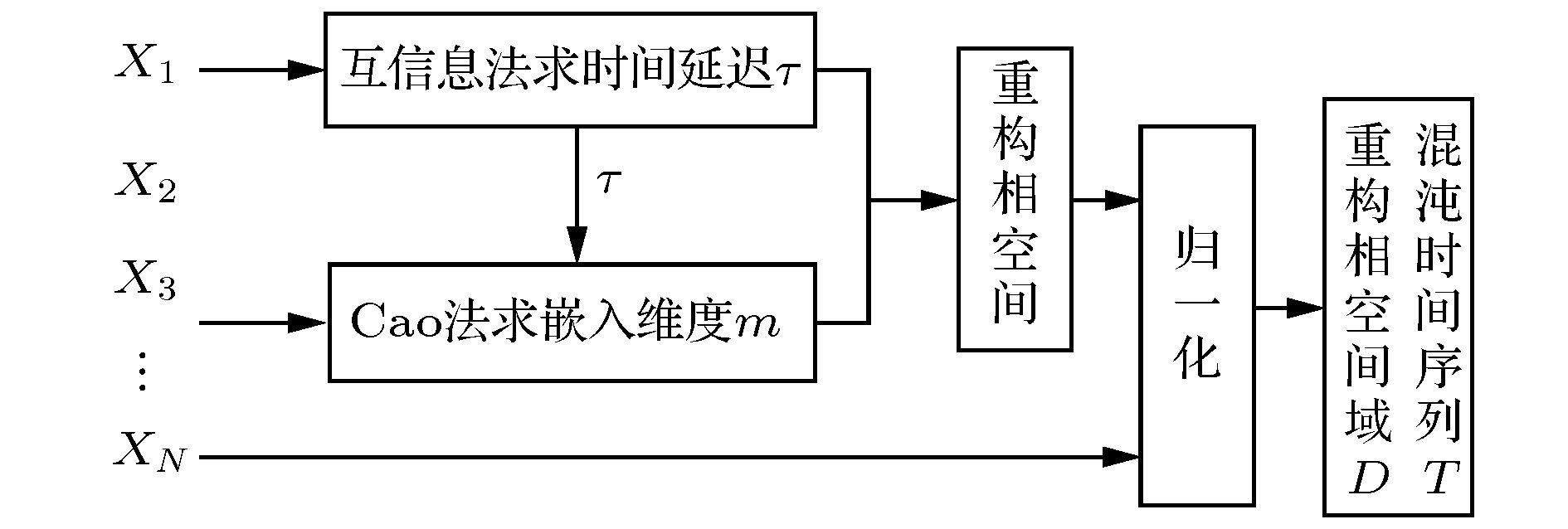
-
为提高混沌时间序列的预测精度, 提出一种基于混合神经网络和注意力机制的预测模型(Att-CNN-LSTM), 首先对混沌时间序列进行相空间重构和数据归一化, 然后利用卷积神经网络(CNN)对时间序列的重构相空间进行空间特征提取, 再将CNN提取的特征和原时间序列组合, 用长短期记忆网络(LSTM)根据空间特征提取时间特征, 最后通过注意力机制捕获时间序列的关键时空特征, 给出最终预测结果. 将该模型对Logistic, Lorenz和太阳黑子混沌时间序列进行预测实验, 并与未引入注意力机制的CNN-LSTM模型、单一的CNN和LSTM网络模型、以及传统的机器学习算法最小二乘支持向量机(LSSVM)的预测性能进行比较. 实验结果显示本文提出的预测模型预测误差低于其他模型, 预测精度更高.Chaotic time series forecasting has been widely used in various domains, and the accurate predicting of the chaotic time series plays a critical role in many public events. Recently, various deep learning algorithms have been used to forecast chaotic time series and achieved good prediction performance. In order to improve the prediction accuracy of chaotic time series, a prediction model (Att-CNN-LSTM) is proposed based on hybrid neural network and attention mechanism. In this paper, the convolutional neural network (CNN) and long short-term memory (LSTM) are used to form a hybrid neural network. In addition, a attention model with softmax activation function is designed to extract the key features. Firstly, phase space reconstruction and data normalization are performed on a chaotic time series, then convolutional neural network (CNN) is used to extract the spatial features of the reconstructed phase space, then the features extracted by CNN are combined with the original chaotic time series, and in the long short-term memory network (LSTM) the combined vector is used to extract the temporal features. And then attention mechanism captures the key spatial-temporal features of chaotic time series. Finally, the prediction results are computed by using spatial-temporal features. To verify the prediction performance of the proposed hybrid model, it is used to predict the Logistic, Lorenz and sunspot chaotic time series. Four kinds of error criteria and model running times are used to evaluate the performance of predictive model. The proposed model is compared with hybrid CNN-LSTM model, the single CNN and LSTM network model and least squares support vector machine(LSSVM), and the experimental results show that the proposed hybrid model has a higher prediction accuracy.
-
Keywords:
- chaotic time series /
- convolutional neural network /
- long short-term memory network /
- attention mechanism
[1] 王世元, 史春芬, 钱国兵, 王万里 2018 67 018401
Google Scholar
Wang S Y, Shi C F, Qian G B, Wang W L 2018 Acta Phys. Sin. 67 018401
Google Scholar
[2] 梅英, 谭冠政, 刘振焘, 武鹤 2018 67 080502
Google Scholar
Mei Y, Tan G Z, Liu Z T, Wu H 2018 Acta Phys. Sin. 67 080502
Google Scholar
[3] 沈力华, 陈吉红, 曾志刚, 金健 2018 67 030501
Google Scholar
Shen L H, Chen J H, Zeng Z G, Jin J 2018 Acta Phys. Sin. 67 030501
Google Scholar
[4] Han M, Zhang S, Xu M, Qiu T, Wang N 2019 IEEE Trans. Cybern. 49 1160
Google Scholar
[5] Han M, Zhang R, Qiu T, Xu M, Ren W 2019 IEEE Trans. Syst. Man Cybern 49 2144
Google Scholar
[6] Safari N, Chung C Y, Price G C D 2018 IEEE Trans. Power Syst. 33 590
Google Scholar
[7] 熊有成, 赵鸿 2019 中国科学: 物理学 力学 天文学 49 92
Xiong Y C, Zhao H 2019 Sci. China, Ser. G 49 92
[8] Sangiorgio M, Dercole F 2020 Chaos, Solitons Fractals 139 110045
Google Scholar
[9] 李世玺, 孙宪坤, 尹玲, 张仕森 2020 导航定位学报 8 65
Google Scholar
Li S X, Sun X K, Yin L, Zhang S S 2020 Journal of Navigation and Positionina 8 65
Google Scholar
[10] Boullé N, Dallas V, Nakatsukasa Y, Samaddar D 2019 Physica D 403 132261
Google Scholar
[11] 唐舟进, 任峰, 彭涛, 王文博 2014 63 050505
Google Scholar
Tang Z J, Ren F, Peng T, Wang W B 2014 Acta Phys. Sin. 63 050505
Google Scholar
[12] 田中大, 高宪文, 石彤 2014 63 160508
Google Scholar
Tian Z D, Gao X W, Shi T 2014 Acta Phys. Sin. 63 160508
Google Scholar
[13] 王新迎, 韩敏 2015 64 070504
Google Scholar
Wang Y X, Han M 2015 Acta Phys. Sin. 64 070504
Google Scholar
[14] 吕金虎 2002 混沌时间序列分析及其应用 (武汉: 武汉大学出版社) 第57−60页
Lu J H 2002 Chaotic Time Series Analysis and Application (Wuhan: Wuhan University Press) pp57−60 (in Chinese)
[15] Packard N, Crutchfield J P, Shaw R 1980 Phys. Rev. Lett. 45 712
Google Scholar
[16] Takens F 1981 Dynamical Systems and Turbulence (Berlin: Springer) pp366−381
[17] Martinerie J M, Albano A M, Mees A I, Rapp P E 1992 Phys. Rev. A 45 7058
Google Scholar
[18] Liangyue C 1997 Physica D 110 43
Google Scholar
[19] Lecun Y, Boser B, Denker J, Henderson D, Howard R, Hubbard W, Jackel L 1989 Neural Comput. 1 541
Google Scholar
[20] Goodfellow I, Bengio Y, Courville A 2016 Deep Learning (Cambridge: The MIT Press) p326
[21] Kim Y 2014 arXiv: 1408.5882 [cs.CL]
[22] Pascanu R, Mikolov T, Bengio Y 2013 Proceedings of the 30th International Conference on International Conference on Machine Learning Atlanta, USA, June 16−21 2013, p1310
[23] Hochreiter S, Schmidhuber J 1997 Neural Comput. 9 1735
Google Scholar
[24] Chung J, Gulcehre C, Cho K, Bengio Y 2014 arXiv: 1412.3555 [cs.NE]
[25] Mnih V, Heess N, Graves A, Kavukcuoglu K 2014 Proceedings of the 27th International Conference on Neural Information Processing Systems Montreal, Canada, December 8−13 2014, p2204
[26] Yin W, Schütze H, Xiang B, Zhou B 2015 arXiv: 1512.05193 [cs.CL]
[27] Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez A N, Kaiser L, Polosukhin I 2017 Proceedings of the 31st International Conference on Neural Information Processing Systems Long Beach, USA, December 4−9 2017, p6000
-
表 1 模型误差对比
Table 1. Model error comparison.
RMSE MAE MAPE RMSPE Att-CNN-LSTM 0.003503 0.002935 0.5305 0.6767 CNN-LSTM 0.006856 0.005444 1.1064 1.7795 LSTM 0.006169 0.005316 1.1595 1.6887 CNN 0.004670 0.003849 0.8802 1.4019 LSSVM 0.009158 0.004307 1.3623 3.8604 
下载: 导出CSV
表 2 模型运行时间对比
Table 2. Model running time comparison.
模型 Att-CNN-LSTM CNN-LSTM CNN LSTM LSSVM 训练时间 /s 312.7 302 59.5 48.8 215.4 预测时间 /s 0.53 0.49 0.25 0.21 0.47
下载: 导出CSV
表 3 模型误差对比
Table 3. Model error comparison.
RMSE MAE MAPE RMSPE Att-CNN-LSTM 0.0679 0.0521 1.2182 2.1102 CNN-LSTM 0.2445 0.1229 3.8849 14.7893 LSTM 0.5152 0.3901 13.6767 43.7676 CNN 0.5356 0.3811 11.0032 33.5251 LSSVM 0.5101 0.3652 9.3543 35.5644
下载: 导出CSV
表 4 模型运行时间对比
Table 4. Model running time comparison.
模型 Att-CNN-LSTM CNN-LSTM CNN LSTM LSSVM 训练时间 /s 184.6 193.9 84.28 51.21 202.4 预测时间 /s 0.47 0.55 0.20 0.23 0.45
下载: 导出CSV
表 5 模型误差对比
Table 5. Model error comparison.
RMSE MAE MAPE RMSPE Att-CNN-LSTM 20.1829 17.1827 32.8167 42.3529 CNN-LSTM 30.5652 21.4093 67.4343 56.7217 LSTM 24.9137 18.2815 49.5862 62.6939 CNN 24.8534 18.4677 65.3480 44.1892 LSSVM 27.3271 19.4373 43.0987 56.6781
下载: 导出CSV
表 6 模型运行时间对比
Table 6. Model running time comparison.
模型 Att-CNN-LSTM CNN-LSTM CNN LSTM LSSVM 训练时间 /s 309.2 291.3 76.5 53.3 237.9 预测时间 /s 0.39 0.43 0.15 0.25 0.59
下载: 导出CSV
-
[1] 王世元, 史春芬, 钱国兵, 王万里 2018 67 018401
Google Scholar
Wang S Y, Shi C F, Qian G B, Wang W L 2018 Acta Phys. Sin. 67 018401
Google Scholar
[2] 梅英, 谭冠政, 刘振焘, 武鹤 2018 67 080502
Google Scholar
Mei Y, Tan G Z, Liu Z T, Wu H 2018 Acta Phys. Sin. 67 080502
Google Scholar
[3] 沈力华, 陈吉红, 曾志刚, 金健 2018 67 030501
Google Scholar
Shen L H, Chen J H, Zeng Z G, Jin J 2018 Acta Phys. Sin. 67 030501
Google Scholar
[4] Han M, Zhang S, Xu M, Qiu T, Wang N 2019 IEEE Trans. Cybern. 49 1160
Google Scholar
[5] Han M, Zhang R, Qiu T, Xu M, Ren W 2019 IEEE Trans. Syst. Man Cybern 49 2144
Google Scholar
[6] Safari N, Chung C Y, Price G C D 2018 IEEE Trans. Power Syst. 33 590
Google Scholar
[7] 熊有成, 赵鸿 2019 中国科学: 物理学 力学 天文学 49 92
Xiong Y C, Zhao H 2019 Sci. China, Ser. G 49 92
[8] Sangiorgio M, Dercole F 2020 Chaos, Solitons Fractals 139 110045
Google Scholar
[9] 李世玺, 孙宪坤, 尹玲, 张仕森 2020 导航定位学报 8 65
Google Scholar
Li S X, Sun X K, Yin L, Zhang S S 2020 Journal of Navigation and Positionina 8 65
Google Scholar
[10] Boullé N, Dallas V, Nakatsukasa Y, Samaddar D 2019 Physica D 403 132261
Google Scholar
[11] 唐舟进, 任峰, 彭涛, 王文博 2014 63 050505
Google Scholar
Tang Z J, Ren F, Peng T, Wang W B 2014 Acta Phys. Sin. 63 050505
Google Scholar
[12] 田中大, 高宪文, 石彤 2014 63 160508
Google Scholar
Tian Z D, Gao X W, Shi T 2014 Acta Phys. Sin. 63 160508
Google Scholar
[13] 王新迎, 韩敏 2015 64 070504
Google Scholar
Wang Y X, Han M 2015 Acta Phys. Sin. 64 070504
Google Scholar
[14] 吕金虎 2002 混沌时间序列分析及其应用 (武汉: 武汉大学出版社) 第57−60页
Lu J H 2002 Chaotic Time Series Analysis and Application (Wuhan: Wuhan University Press) pp57−60 (in Chinese)
[15] Packard N, Crutchfield J P, Shaw R 1980 Phys. Rev. Lett. 45 712
Google Scholar
[16] Takens F 1981 Dynamical Systems and Turbulence (Berlin: Springer) pp366−381
[17] Martinerie J M, Albano A M, Mees A I, Rapp P E 1992 Phys. Rev. A 45 7058
Google Scholar
[18] Liangyue C 1997 Physica D 110 43
Google Scholar
[19] Lecun Y, Boser B, Denker J, Henderson D, Howard R, Hubbard W, Jackel L 1989 Neural Comput. 1 541
Google Scholar
[20] Goodfellow I, Bengio Y, Courville A 2016 Deep Learning (Cambridge: The MIT Press) p326
[21] Kim Y 2014 arXiv: 1408.5882 [cs.CL]
[22] Pascanu R, Mikolov T, Bengio Y 2013 Proceedings of the 30th International Conference on International Conference on Machine Learning Atlanta, USA, June 16−21 2013, p1310
[23] Hochreiter S, Schmidhuber J 1997 Neural Comput. 9 1735
Google Scholar
[24] Chung J, Gulcehre C, Cho K, Bengio Y 2014 arXiv: 1412.3555 [cs.NE]
[25] Mnih V, Heess N, Graves A, Kavukcuoglu K 2014 Proceedings of the 27th International Conference on Neural Information Processing Systems Montreal, Canada, December 8−13 2014, p2204
[26] Yin W, Schütze H, Xiang B, Zhou B 2015 arXiv: 1512.05193 [cs.CL]
[27] Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez A N, Kaiser L, Polosukhin I 2017 Proceedings of the 31st International Conference on Neural Information Processing Systems Long Beach, USA, December 4−9 2017, p6000
下载:
计量
- 文章访问数: 12004
- PDF下载量: 535
- 被引次数: 0
