-
中国聚变工程实验堆(CFETR)是我国自主设计和研制的新一代磁约束聚变装置. 基于快波的色散关系, 通过理论分析和数值求解等离子体色散函数
$ Z(\xi )$ , 获得了螺旋波(快磁声波)与等离子体相互作用波阻尼因子G与等离子体参数和波频率等的关系. 研究结果表明: 在CFETR等离子体放电参数下, 螺旋波能够产生显著的离轴波功率沉积和波驱动电流, 波与等离子体相互作用的主要物理机制是电子朗道阻尼. 此外, 螺旋波阻尼系数与发射波(谱)的平行折射率和等离子体参数密切相关, 但总是随着波频率增加而变大. 对CFETR装置混合运行模式的GENRAY/CQL3D模拟研究结果表明, 800 MHz的螺旋波能够在$ r \approx 0.5a$ 处产生显著的波功率沉积和波驱动电流, 驱动电流的效率约为50 kA/MW.The Chinese fusion engineering testing reactor (CFETR), complementing the ITER facility, is aimed at building up the science and technology base for the prototype of fusion power plant (PFPP). Based on the dispersion relation of fast wave, the analysis of the plasma dispersion function$ Z(\xi )$ is performed and a numerical solution of$ Z(\xi )$ is obtained. As the consequence, the dependence of helicon wave damping factor G on the plasma parameters and that on the wave properties are both achieved. The results show that an off-axis power deposition of the wave along the device radius can be achieved under the condition of plasma discharge on CFETR tokamak. Moreover, by calculating the ratio of the electron Alfven damping in the ion cyclotron range of frequencies to the electron Landau damping, we find that the electron Alfven damping is dominant at lower wave frequencies. With the wave frequency increasing, the electron Alfven damping remains unchanged while the Landau damping increases rapidly. With the discharge parameters of CTETR hybrid mode, the electron Landau damping proves to be dominant. Moreover, the off-axis power deposition and current drive profiles are produced. It is shown that the helicon wave damping factor increases with wave frequency increasing and it is closely related to the parallel refractive index of the injected wave spectrum, the plasma density, and plasma temperature. Significant off-axis power deposition and current drive are shown in CTETR hybrid mode operation, and the current drive efficiency reaches 50 kA/MW for helicon wave with a frequency of 800 MHz. Numerical simulation performed on the GENRAY/CQL3d shows a good consistence with the experimental results.-
Keywords:
- helicon wave /
- Chinese fusion engineering testing reactor /
- plasma dispersion function /
- electron landau damping
[1] Vdovin V L 2013 Plasma Phys. Rep. 39 95
Google Scholar
[2] Prater R, Moeller C P, Pinsker R I, Porkolab M, Meneghini O, Vdovin V L 2014 Nucl. Fusion 54 083024
Google Scholar
[3] Fischer B, Kramer M, Enk T 1994 Plasma Phys. Controlled Fusion 36 2003
Google Scholar
[4] Chiu S C, Chan V S, Harvey R W, Porkolab M 1989 Nucl. Fusion 29 2175
Google Scholar
[5] Fisch N 1987 Rev. Mod. Phys. 59 175
Google Scholar
[6] Fried B D, Hedrick C, McCune J 1968 Phys. Fluids 11 249252
[7] Martin P, Donoso G, Zamudio J 1980 J. Math. Phys. 21 280
Google Scholar
[8] Nemeth G, Paris G 1981 J. Plasma Phys. 22 11921195
[9] 刘红秀 1986 核聚变与等离子体物理 1 4850
Liu H X 1986 Nucl. Fus. Plasma Phys. 1 4850
[10] 牟宗泽, 赵怀国 1994 计算物理 11 367374
Mou Z Z, Zhao H G 1994 Chin. J. Comput. Phys. 11 367374
[11] Stix T H 1992 Waves in Plasmas (New York: AIP Press) pp256−262
[12] Wave in Warm Plasma, Richard F http://farside.ph.utexas.edu/teaching/plasma/Plasmahtml/node83.html [2011−03−31]
[13] Harvey R W, Smirnov AP 2001 CompX Report CompX-2000-01
[14] Wan Y X, Li J G, Liu Y, Wang X L 2017 Nucl. Fusion 57 102009
Google Scholar
[15] Li J G, Wan Y X 2019 J. Fusion Energy 38 113
Google Scholar
[16] Zhuang G, Li G Q, Li J, Wan Y X, Liu Y, Wang X L, Song Y T, Chan V, Yang Q W 2019 Nucl. Fusion 59 112010
Google Scholar
[17] 平兰兰, 张新军, 杨桦, 徐国盛, 苌磊, 吴东升, 吕虹, 郑长勇, 彭金花, 金海红, 何超, 甘桂华 2019 68 205201
Google Scholar
Ping L L, Zhang X J, Yang H, Xu G S, Chang L, Wu D S, Lv H, Zheng C Y, Peng J H, Jin H H, He C, Gan G H 2019 Acta Phys. Sin. 68 205201
Google Scholar
[18] Chen J L 2019 CFETR Integrated Engineering Design Annual Meeting and Fusion Reactor Design Seminar. Huangshan, China, September 23−29, 2019
[19] Cheng Y, Bonoli P, Wright J, Ding B, Parker R, Shiraiwa S, Li M 2014 Plasma Phys. Controlled Fusion 56 125003
Google Scholar
[20] Petrov Y V, Harvey R W 2016 Plasma Phys. Controlled Fusion 58 115001
Google Scholar
-
图 1 色散函数及其实部和虚部值随
$\xi$ 变化Fig. 1. The dependence of
$Z(\xi )$ and its components on$\xi$ .
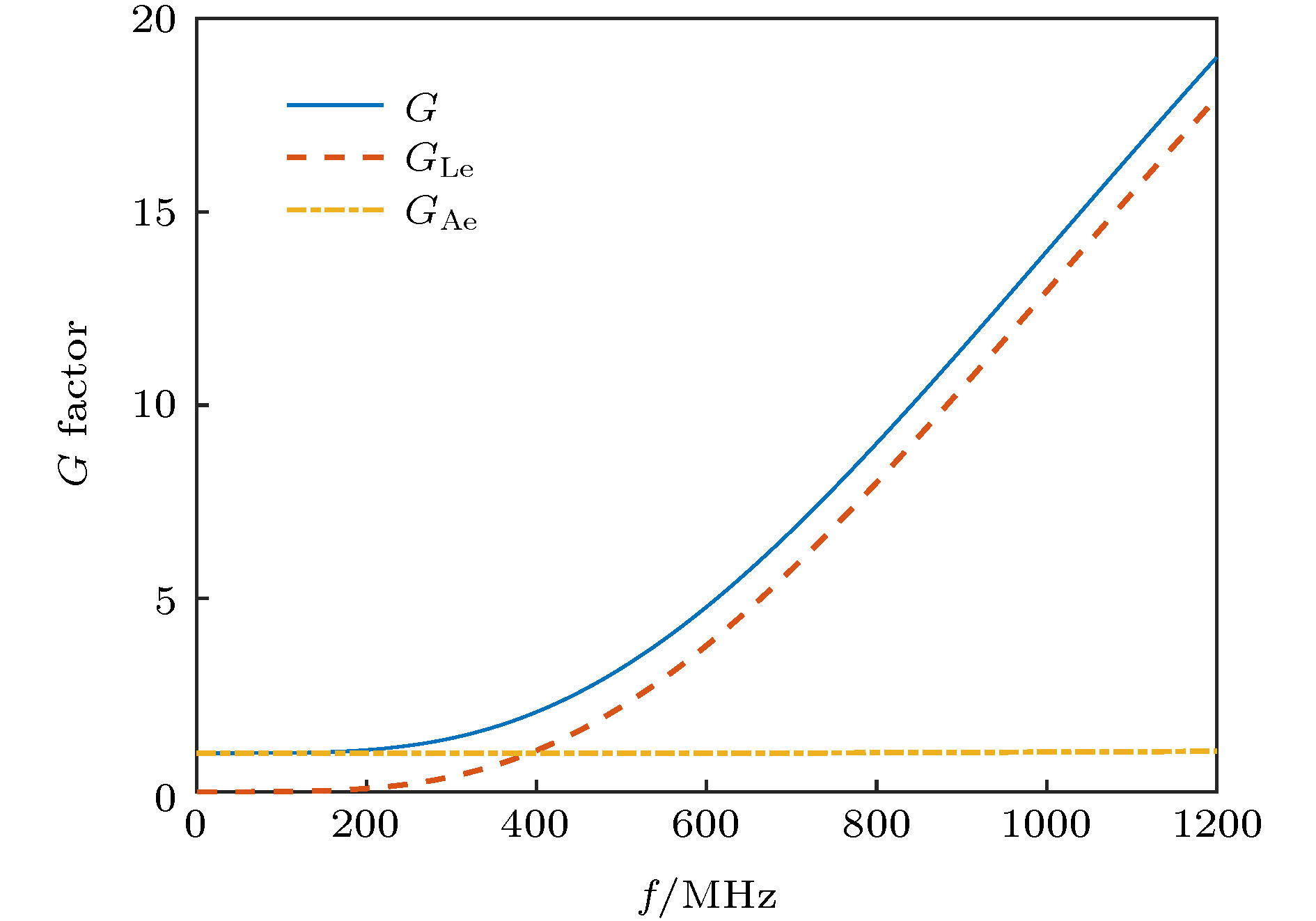
图 2 波阻尼因子G、电子阿尔芬阻尼因子GAe和朗道阻尼因子GLe与波频率的关系,
$ {T_{\rm{e}}} = 20\;{\rm{ keV}}$ , ne0 = 1 × 1020 m–3, B = 5 T,$ B = 5\;{\rm{T}}$ ,${n_{/\!/}} = 2.0$ Fig. 2. The relationship of the wave damping factor on wave frequency. The parameters used here are
${T_{\rm{e}}} = 20\;{\rm{ keV}}$ , ne0 = 1 × 1020 m–3, B = 5 T,${n_{/\!/}} = 2.0$ .
图 3 波折射率
${n_{/\!/}}$ 和等离子体密度对波阻尼因子G的影响, 等离子体温度${T_{\rm{e}}} = 20\;{\rm{ keV}}$ , 磁场$B = 5\;{\rm{ T}}$ Fig. 3. The effect of wave initial parallel refractive index
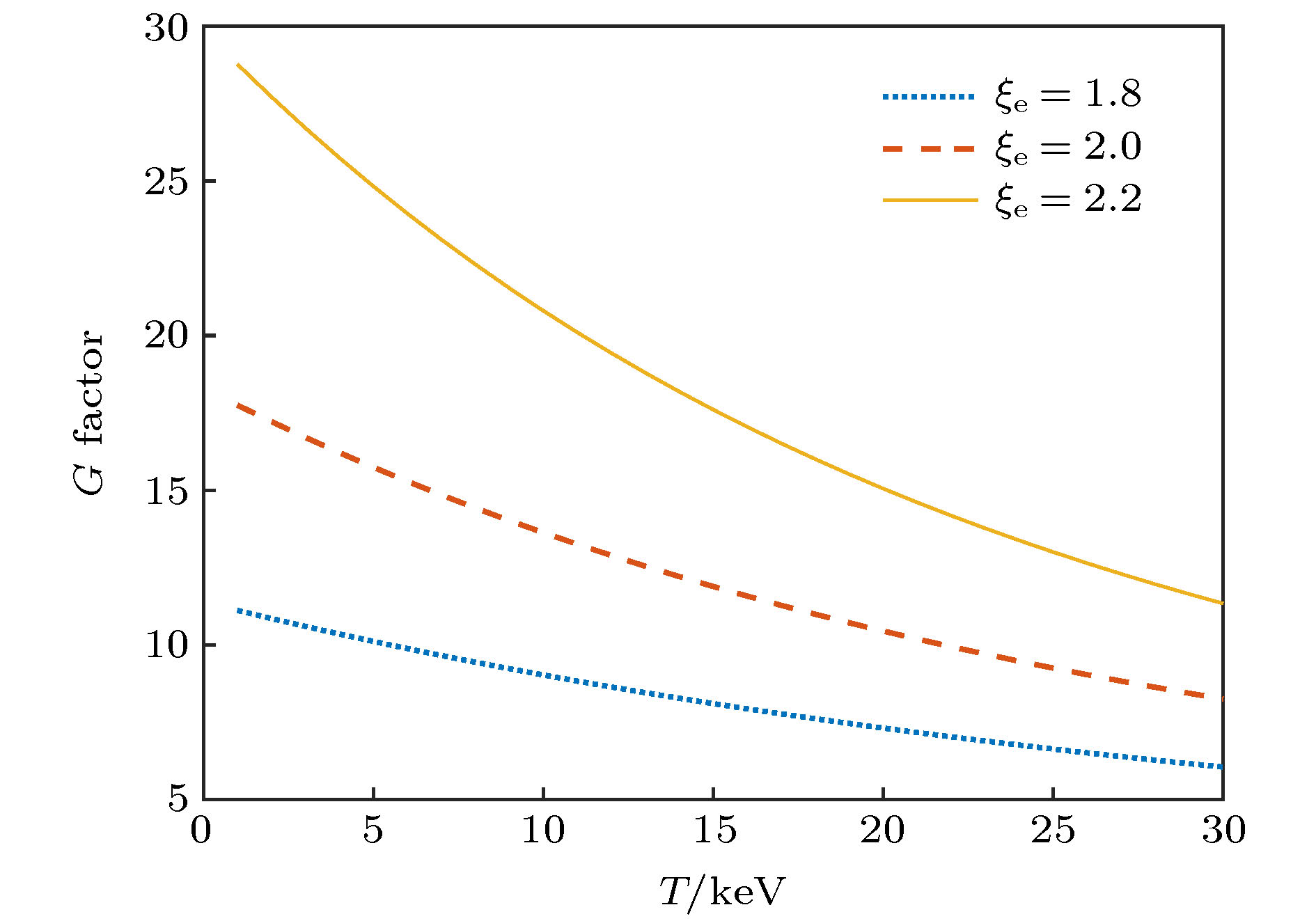
${n_{/\!/}}$ and plasma density on wave damping factor. The plasma temperature is${T_{\rm{e}}} = 20\;{\rm{ keV}}$ , magnetic filed$B = 5\;{\rm{ T}}$ .
图 4 螺旋波阻尼因子G随等离子体温度的变化, 波频率f = 800 MHz, 电子密度
$ {n_{{\rm{e0}}}} = {\rm{1}} \times {\rm{1}}{0^{{\rm{2}}0}}\;{{\rm{m}}^{ - {\rm{3}}}}$ , 磁场B = 5.0 TFig. 4. The dependence of wave damping factor G on plasma temperature. The parameters used here are f = 800 MHz,
${n_{{\rm{e}}0}} = {\rm{1}} \times {\rm{1}}{0^{{\rm{2}}0}}\;{{\rm{m}}^{ - {\rm{3}}}}$ , B = 5.0 T.
图 5 CFETR装置波阻尼率随等离子体温度的变化
Fig. 5. The relationship between the damping ratio and the wave frequency on CFETR.
图 6 CFETR混合运行模式下螺旋波波功率沉积密度剖面分布, 入射波功率
$P=1\;{\rm{ MW}}$ , 平行折射率${n_{/\!/}}=2.5$ , 波频率$f=800\;{\rm{ MHz}}$ Fig. 6. The power deposition density profile of helicon wave under the CFETR hybrid mode, the power inject is
$P=1\;{\rm{ MW}}$ , parallel refractive index${n_{/\!/}}=2.5$ , the wave frequency is 800 MHz.
表 1 等离子体色散函数数值结果比较
Table 1. Numerical results of plasma dispersion function.
数值计算结果 数表结果[10] ξ ZR ZI ZR ZI 0 0 0.177245×101 0 0.177245×101 0.2 –0.389502 0.170296×101 –0.389502 0.170295×101 0.4 –0.719887 0.151039×101 0.719887 0.151039×101 0.6 –0.949526 0.123660×101 –0.949256 0.123660×101 1.0 –1.076159 0.652049×100 1.076160 0.652049×100 2.0 –0.602681 0.324636×10–1 0.602681 0.324636×10–1 4.0 –0.258696 0.199463×10–6 0.258696 0.199463×10–6 6.0 –0.169085 0.411125×10–15 0.169086 0.411124×10–15 
下载: 导出CSV
-
[1] Vdovin V L 2013 Plasma Phys. Rep. 39 95
Google Scholar
[2] Prater R, Moeller C P, Pinsker R I, Porkolab M, Meneghini O, Vdovin V L 2014 Nucl. Fusion 54 083024
Google Scholar
[3] Fischer B, Kramer M, Enk T 1994 Plasma Phys. Controlled Fusion 36 2003
Google Scholar
[4] Chiu S C, Chan V S, Harvey R W, Porkolab M 1989 Nucl. Fusion 29 2175
Google Scholar
[5] Fisch N 1987 Rev. Mod. Phys. 59 175
Google Scholar
[6] Fried B D, Hedrick C, McCune J 1968 Phys. Fluids 11 249252
[7] Martin P, Donoso G, Zamudio J 1980 J. Math. Phys. 21 280
Google Scholar
[8] Nemeth G, Paris G 1981 J. Plasma Phys. 22 11921195
[9] 刘红秀 1986 核聚变与等离子体物理 1 4850
Liu H X 1986 Nucl. Fus. Plasma Phys. 1 4850
[10] 牟宗泽, 赵怀国 1994 计算物理 11 367374
Mou Z Z, Zhao H G 1994 Chin. J. Comput. Phys. 11 367374
[11] Stix T H 1992 Waves in Plasmas (New York: AIP Press) pp256−262
[12] Wave in Warm Plasma, Richard F http://farside.ph.utexas.edu/teaching/plasma/Plasmahtml/node83.html [2011−03−31]
[13] Harvey R W, Smirnov AP 2001 CompX Report CompX-2000-01
[14] Wan Y X, Li J G, Liu Y, Wang X L 2017 Nucl. Fusion 57 102009
Google Scholar
[15] Li J G, Wan Y X 2019 J. Fusion Energy 38 113
Google Scholar
[16] Zhuang G, Li G Q, Li J, Wan Y X, Liu Y, Wang X L, Song Y T, Chan V, Yang Q W 2019 Nucl. Fusion 59 112010
Google Scholar
[17] 平兰兰, 张新军, 杨桦, 徐国盛, 苌磊, 吴东升, 吕虹, 郑长勇, 彭金花, 金海红, 何超, 甘桂华 2019 68 205201
Google Scholar
Ping L L, Zhang X J, Yang H, Xu G S, Chang L, Wu D S, Lv H, Zheng C Y, Peng J H, Jin H H, He C, Gan G H 2019 Acta Phys. Sin. 68 205201
Google Scholar
[18] Chen J L 2019 CFETR Integrated Engineering Design Annual Meeting and Fusion Reactor Design Seminar. Huangshan, China, September 23−29, 2019
[19] Cheng Y, Bonoli P, Wright J, Ding B, Parker R, Shiraiwa S, Li M 2014 Plasma Phys. Controlled Fusion 56 125003
Google Scholar
[20] Petrov Y V, Harvey R W 2016 Plasma Phys. Controlled Fusion 58 115001
Google Scholar
下载:
计量
- 文章访问数: 7432
- PDF下载量: 94
- 被引次数: 0
