-
太赫兹辅助光电离瞬态测量方法可以分辨超快量子拍频, 同时对复杂量子系统的超快密度矩阵演化进行成像. 本文依据这种方法提出了一种具体的实验方案, 利用紫外脉冲(脉宽为30 fs)和高强度太赫兹脉冲(峰值场强: 约1 MV/cm)组成复合探测电场, 探测铷原子
$5 {\mathrm{S}}_{1/2} $ 和$5 {\mathrm{P}}_{3/2} $ 叠加态振荡周期约为2.6 fs的量子拍频过程, 量子体系密度矩阵演化的布居项和相干项投影在光电子动量谱的不同位置, 可以对密度矩阵演化实现完全信息测量. 本文设计的实验方案不需要阿秒高次谐波或自由电子激光等复杂的先进光源, 可以成为探索复杂量子体系超快相干动力学过程的新方案.Terahertz-streaking photoionization can be exploited to resolve ultrafast quantum beating and reconstruct the ultrafast evolution of density matrix. Here, we propose an experimental strategy to implement the method merely with the tabletop femtosecond system and magneto-optical trap reaction microscopy. The probe pulse consists of an ultraviolet pulse with pulse duration of about 30 fs and a strong terahertz pulse with strength of about 2.6 fs in rubidium-atom superposition. The population and coherence terms of the density matrix can be projected into different positions of the photoelectron momentum distribution. The reconstruction algorithm was designed to acquire the ultrafast evolution of density matrix from the time-dependent photoelectron spectrum. The experimental conception can demonstrate the newly proposed transient spectral method only with the commercial femtosecond laser system and magneto-optical trap reaction microscopy, thus preventing the complex laser system, such as extreme ultraviolet free electron lasers and attosecond higher harmonics, allowing a new metrology to explore the coherence dynamics of quantum systems.[1] Pabst S, Greenman L, Ho P J, Mazziotti D A, Santra R 2011 Phys. Rev. Lett. 106 053003
Google Scholar
[2] Arnold C, Vendrell O, Santra R 2017 Phys. Rev. A 95 033425
Google Scholar
[3] Willenberg B, Maurer J, Mayer B W, Keller U 2019 Nat. Commun. 10 5548
Google Scholar
[4] Hartung A, Eckart S, Brennecke S, Rist J, Trabert D, Fehre K, Richter M, Sann H, Zeller S, Henrichs K, Kastirke G, Hoehl J, Kalinin A, Schöffler M S, Jahnke T, Schmidt L P H, Lein M, Kunitski M, Dörner R 2019 Nat. Phys. 15 1222
Google Scholar
[5] Collini E, Scholes G D 2009 Science 323 369
Google Scholar
[6] Collini E, Wong C Y, Wilk K E, Curmi P M G, Brumer P, Scholes G D 2010 Nature 463 644
Google Scholar
[7] Engel G S, Calhoun T R, Read E L, Ahn T K, Mančal T, Cheng Y C, Blankenship R E, Fleming G R 2007 Nature 446 782
Google Scholar
[8] Brixner T, Stenger J, Vaswani H M, Cho M, Blankenship R E, Fleming G R 2005 Nature 434 625
Google Scholar
[9] Meng Q X, Zhang Y Z, Yan T M, Jiang Y H 2017 Opt. Express 25 6644
Google Scholar
[10] Zhang Y Z, Yan T M, Jiang Y H 2016 Opt. Lett. 41 4134
Google Scholar
[11] Kobayashi Y, Chang K F, Zeng T, Neumark D M, Leone S R 2019 Science 365 79
Google Scholar
[12] Goulielmakis E, Loh Z H, Wirth A, Santra R, Rohringer N, Yakovlev V S, Zherebtsov S, Pfeifer T, Azzeer A M, Kling M F, Leone S R, Krausz F 2010 Nature 466 739
Google Scholar
[13] Ott C, Kaldun A, Argenti L, Raith P, Meyer K, Laux M, Zhang Y, Blättermann A, Hagstotz S, Ding T, Heck R, Madroñero J, Martín F, Pfeifer T 2014 Nature 516 374
Google Scholar
[14] Ott C, Aufleger L, Ding T, Rebholz M, Magunia A, Hartmann M, Stooß V, Wachs D, Birk P, Borisova G D, Meyer K, Rupprecht P, da Costa Castanheira C, Moshammer R, Attar A R, Gaumnitz T, Loh Z H, Düsterer S, Treusch R, Ullrich J, Jiang Y H, Meyer M, Lambropoulos P, Pfeifer T 2019 Phys. Rev. Lett. 123 163201
Google Scholar
[15] Kowalewski M, Bennett K, Rouxel J R, Mukamel S 2016 Phys. Rev. Lett. 117 043201
Google Scholar
[16] Zhang Y Z, Yan T M, Jiang Y H 2018 Phys. Rev. Lett. 121 113201
Google Scholar
[17] Deutsch C, Ramirez-Martinez F, Lacroute C, Reinhard F, Schneider T, Fuchs J N, Piéchon F, Laloe F, Reichel J, Rosenbusch P 2010 Phys. Rev. Lett. 105 020401
Google Scholar
[18] Mudrich M, Stienkemeier F, Droppelmann G, Claas P, Schulz C 2008 Phys. Rev. Lett. 100 023401
Google Scholar
[19] Li R Y, Yuan J Y, Wang X C, Hou X Y, Zhang S, Zhu Z Y, Ma Y X, Gao Q, Wang Z Y, Yan T M, Qin C C, Li S, Zhang Y Z, Weidemüller M, Jiang Y H 2019 J. Instrum. 14 P02022
Google Scholar
[20] Yuan J Y, Ma Y X, Li R Y, Ma H Y, Yan T M, Zhang Y Z, Ye D F, Shen Z J, Wang X C, Weidemuller M, Jiang Y H 2020 Chin. Phys. Lett. 37 053201
Google Scholar
[21] 马祎璇, 李任远, 袁俊阳, 孟秋香, 马欢玉, 阮舒舒, 张逸竹, 阎天民, 沈镇捷, 王新成, 江玉海 2020 中国激光 47 0601011
Google Scholar
Ma Y X, Li R Y, Yuan J Y, Meng Q X, Ma H Y, Ruan S S, Zhang Y Z, Yan T M, Shen Z J, Wang X C, Jiang Y H 2020 Chineses J. Lasers 47 0601011
Google Scholar
[22] Hirori H, Doi A, Blanchard F, Tanaka K 2011 Appl. Phys. Lett. 98 091106
Google Scholar
[23] Ravi K, Huang W R, Carbajo S, Wu X J, Kärtner F 2014 Opt. Express 22 20239
Google Scholar
[24] Wu X J, Carbajo S, Ravi K, Ahr F, Cirmi G, Zhou Y, Mücke O D, Kärtner F X 2014 Opt. Lett. 39 5403
Google Scholar
[25] 黄文逍, 张逸竹, 阎天民, 江玉海 2016 65 223204
Google Scholar
Huang W X, Zhang Y Z, Yan T M, Jiang Y H 2016 Acta Phys. Sin. 65 223204
Google Scholar
[26] Huang Y, Qin C C, Zhang Y Z, Wang X C, Yan T M, Jiang Y H 2019 Chin. Phys. B 28 93202
Google Scholar
-
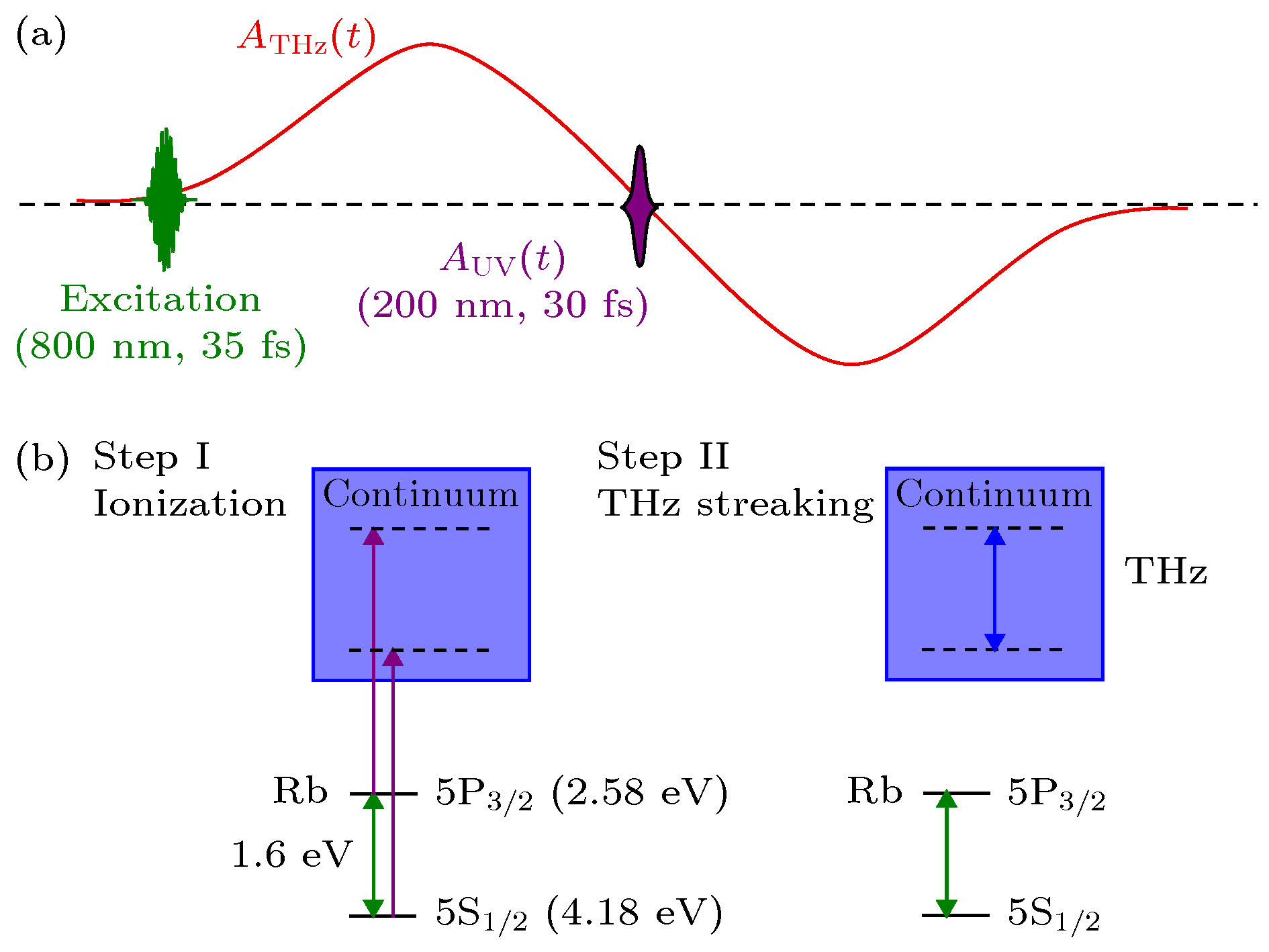
图 1 太赫兹辅助下的铷原子5s和5p能级光电离实验原理图 (a) 探测光含紫外飞秒激光脉冲和太赫兹脉冲, 紫外飞秒脉冲锁定于太赫兹矢势零点处, 将用于探测由红外光制备的铷原子叠加态的相干动力学过程; (b) 太赫兹辅助光电离过程示意图. 第一步, 紫外飞秒激光电离铷原子叠加态电子, 在光电子能谱上形成两条特征谱线; 第二步, 不同末动量的连续电子波函数在太赫兹的驱动下, 能谱展宽并发生干涉现象
Fig. 1. Schematic diagram of terahertz-streaking photoioniza-tion experiments. (a) The probe pulses consist of a ultraviolet pulse and a terahertz pulse. The ultraviolet pulse is locked at the zero point of terahertz vector potential. The superposition state of rubidium atoms is excited by an infrared pulse. (b) Schematic diagram in energy representation. First, the electrons in the superposition state of rubidium atoms are ionized by a UV femtosecond pulse to form two characteristic spectral lines in the photoelectron energy spectrum. Second, the continuous electron with different final momenta is driven by the terahertz pulse. The spectral lines are broadened and the interference occurs.
图 2 光电子动量谱随抽运-探测时间的演化 (a) 仅紫外脉冲电离铷原子情况下光电子的动量谱; (b)太赫兹电场辅助光电离下光电子的动量谱
Fig. 2. The evolution of photoelectron momentum spectra as a function of time delay: (a) Photoelectron momentum spectra without a terahertz field; (b) photoelectron momentum spectra with a terahertz field.
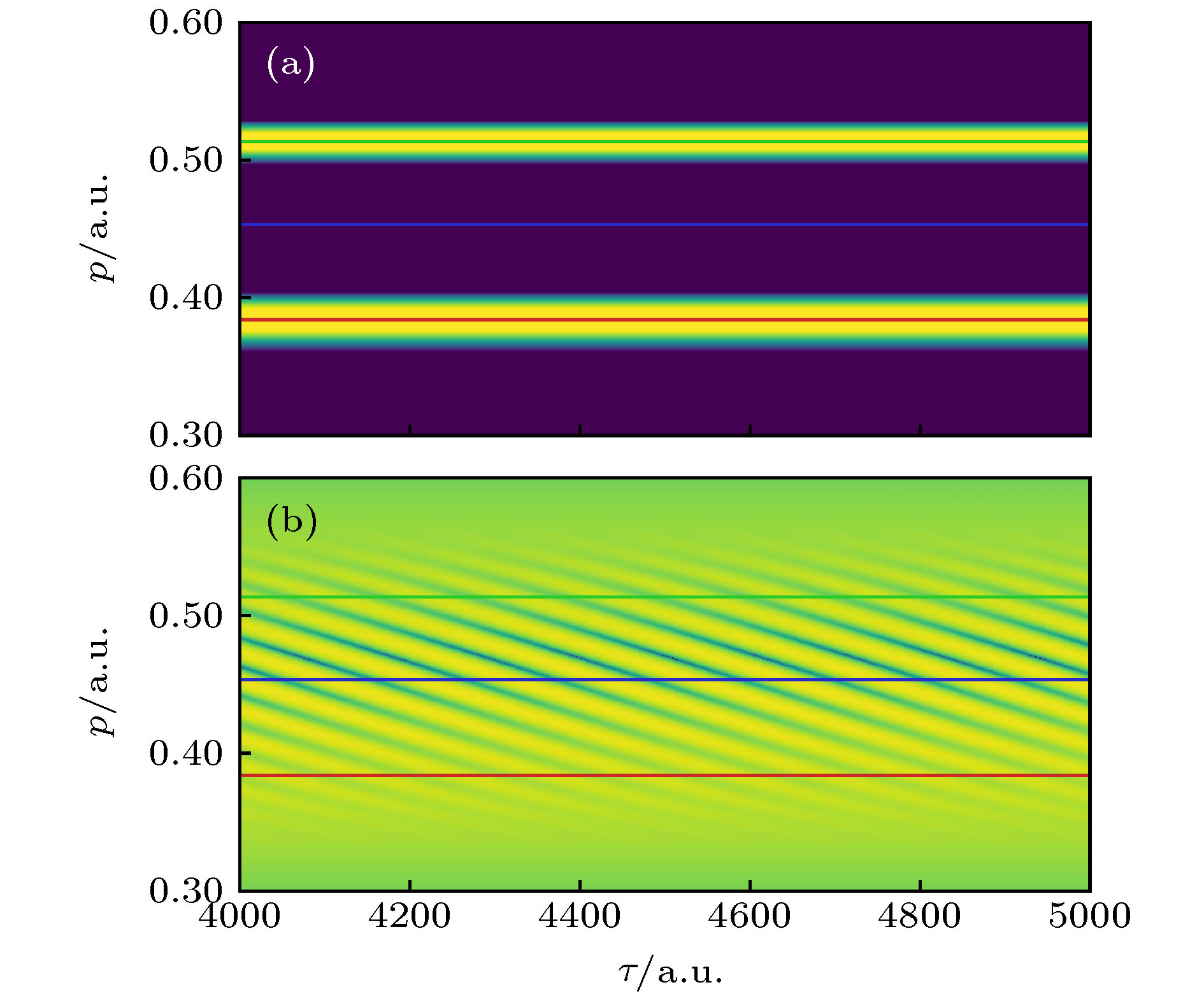
图 3 量子相干信息的时域分辨以及计算与理论的拟合 (a) 重构体系的相干动力学过程, 实线为理论相干项
$ \mathrm{R}\mathrm{e}\left[{\rho }_{\mathrm{e}\mathrm{g}}\left(\tau \right)\right] $ , 虚线为图2(b)中蓝线提取的相干相位信息; (b)黄线为在太赫兹电场驱动下$\tau =4000\mathrm{ }\;\mathrm{a}.\mathrm{u}.$ 时的光电子动量分布, 红线代表布居项贡献, 绿线代表着相干项的贡献Fig. 3. Time-domain resolution of quantum coherence and the reconstruction of density matrix: (a) Coherent dynamics of the quantum system. The solid line is the theoretical prediction of the coherence term
$ \mathrm{R}\mathrm{e}\left[{\rho }_{eg}\left(\tau \right)\right] $ . The dotted line is the cross section along the blue line in Fig. 2 (b) to extract the phase information. (b) Yellow line is the photoelectron momentum distribution driven by THz electric field at$\tau =4000\mathrm{ }\;\mathrm{a}.\mathrm{u}.$ . The red line represents the population contribution; and the green line represents the coherence contribution. -
[1] Pabst S, Greenman L, Ho P J, Mazziotti D A, Santra R 2011 Phys. Rev. Lett. 106 053003
Google Scholar
[2] Arnold C, Vendrell O, Santra R 2017 Phys. Rev. A 95 033425
Google Scholar
[3] Willenberg B, Maurer J, Mayer B W, Keller U 2019 Nat. Commun. 10 5548
Google Scholar
[4] Hartung A, Eckart S, Brennecke S, Rist J, Trabert D, Fehre K, Richter M, Sann H, Zeller S, Henrichs K, Kastirke G, Hoehl J, Kalinin A, Schöffler M S, Jahnke T, Schmidt L P H, Lein M, Kunitski M, Dörner R 2019 Nat. Phys. 15 1222
Google Scholar
[5] Collini E, Scholes G D 2009 Science 323 369
Google Scholar
[6] Collini E, Wong C Y, Wilk K E, Curmi P M G, Brumer P, Scholes G D 2010 Nature 463 644
Google Scholar
[7] Engel G S, Calhoun T R, Read E L, Ahn T K, Mančal T, Cheng Y C, Blankenship R E, Fleming G R 2007 Nature 446 782
Google Scholar
[8] Brixner T, Stenger J, Vaswani H M, Cho M, Blankenship R E, Fleming G R 2005 Nature 434 625
Google Scholar
[9] Meng Q X, Zhang Y Z, Yan T M, Jiang Y H 2017 Opt. Express 25 6644
Google Scholar
[10] Zhang Y Z, Yan T M, Jiang Y H 2016 Opt. Lett. 41 4134
Google Scholar
[11] Kobayashi Y, Chang K F, Zeng T, Neumark D M, Leone S R 2019 Science 365 79
Google Scholar
[12] Goulielmakis E, Loh Z H, Wirth A, Santra R, Rohringer N, Yakovlev V S, Zherebtsov S, Pfeifer T, Azzeer A M, Kling M F, Leone S R, Krausz F 2010 Nature 466 739
Google Scholar
[13] Ott C, Kaldun A, Argenti L, Raith P, Meyer K, Laux M, Zhang Y, Blättermann A, Hagstotz S, Ding T, Heck R, Madroñero J, Martín F, Pfeifer T 2014 Nature 516 374
Google Scholar
[14] Ott C, Aufleger L, Ding T, Rebholz M, Magunia A, Hartmann M, Stooß V, Wachs D, Birk P, Borisova G D, Meyer K, Rupprecht P, da Costa Castanheira C, Moshammer R, Attar A R, Gaumnitz T, Loh Z H, Düsterer S, Treusch R, Ullrich J, Jiang Y H, Meyer M, Lambropoulos P, Pfeifer T 2019 Phys. Rev. Lett. 123 163201
Google Scholar
[15] Kowalewski M, Bennett K, Rouxel J R, Mukamel S 2016 Phys. Rev. Lett. 117 043201
Google Scholar
[16] Zhang Y Z, Yan T M, Jiang Y H 2018 Phys. Rev. Lett. 121 113201
Google Scholar
[17] Deutsch C, Ramirez-Martinez F, Lacroute C, Reinhard F, Schneider T, Fuchs J N, Piéchon F, Laloe F, Reichel J, Rosenbusch P 2010 Phys. Rev. Lett. 105 020401
Google Scholar
[18] Mudrich M, Stienkemeier F, Droppelmann G, Claas P, Schulz C 2008 Phys. Rev. Lett. 100 023401
Google Scholar
[19] Li R Y, Yuan J Y, Wang X C, Hou X Y, Zhang S, Zhu Z Y, Ma Y X, Gao Q, Wang Z Y, Yan T M, Qin C C, Li S, Zhang Y Z, Weidemüller M, Jiang Y H 2019 J. Instrum. 14 P02022
Google Scholar
[20] Yuan J Y, Ma Y X, Li R Y, Ma H Y, Yan T M, Zhang Y Z, Ye D F, Shen Z J, Wang X C, Weidemuller M, Jiang Y H 2020 Chin. Phys. Lett. 37 053201
Google Scholar
[21] 马祎璇, 李任远, 袁俊阳, 孟秋香, 马欢玉, 阮舒舒, 张逸竹, 阎天民, 沈镇捷, 王新成, 江玉海 2020 中国激光 47 0601011
Google Scholar
Ma Y X, Li R Y, Yuan J Y, Meng Q X, Ma H Y, Ruan S S, Zhang Y Z, Yan T M, Shen Z J, Wang X C, Jiang Y H 2020 Chineses J. Lasers 47 0601011
Google Scholar
[22] Hirori H, Doi A, Blanchard F, Tanaka K 2011 Appl. Phys. Lett. 98 091106
Google Scholar
[23] Ravi K, Huang W R, Carbajo S, Wu X J, Kärtner F 2014 Opt. Express 22 20239
Google Scholar
[24] Wu X J, Carbajo S, Ravi K, Ahr F, Cirmi G, Zhou Y, Mücke O D, Kärtner F X 2014 Opt. Lett. 39 5403
Google Scholar
[25] 黄文逍, 张逸竹, 阎天民, 江玉海 2016 65 223204
Google Scholar
Huang W X, Zhang Y Z, Yan T M, Jiang Y H 2016 Acta Phys. Sin. 65 223204
Google Scholar
[26] Huang Y, Qin C C, Zhang Y Z, Wang X C, Yan T M, Jiang Y H 2019 Chin. Phys. B 28 93202
Google Scholar
下载:
计量
- 文章访问数: 6945
- PDF下载量: 86
- 被引次数: 0
