确定大气边界层顶高度的新方法及数值实验

周建印; 项杰; 黄思训

doi:10.7498/aps.69.20191992

摘要

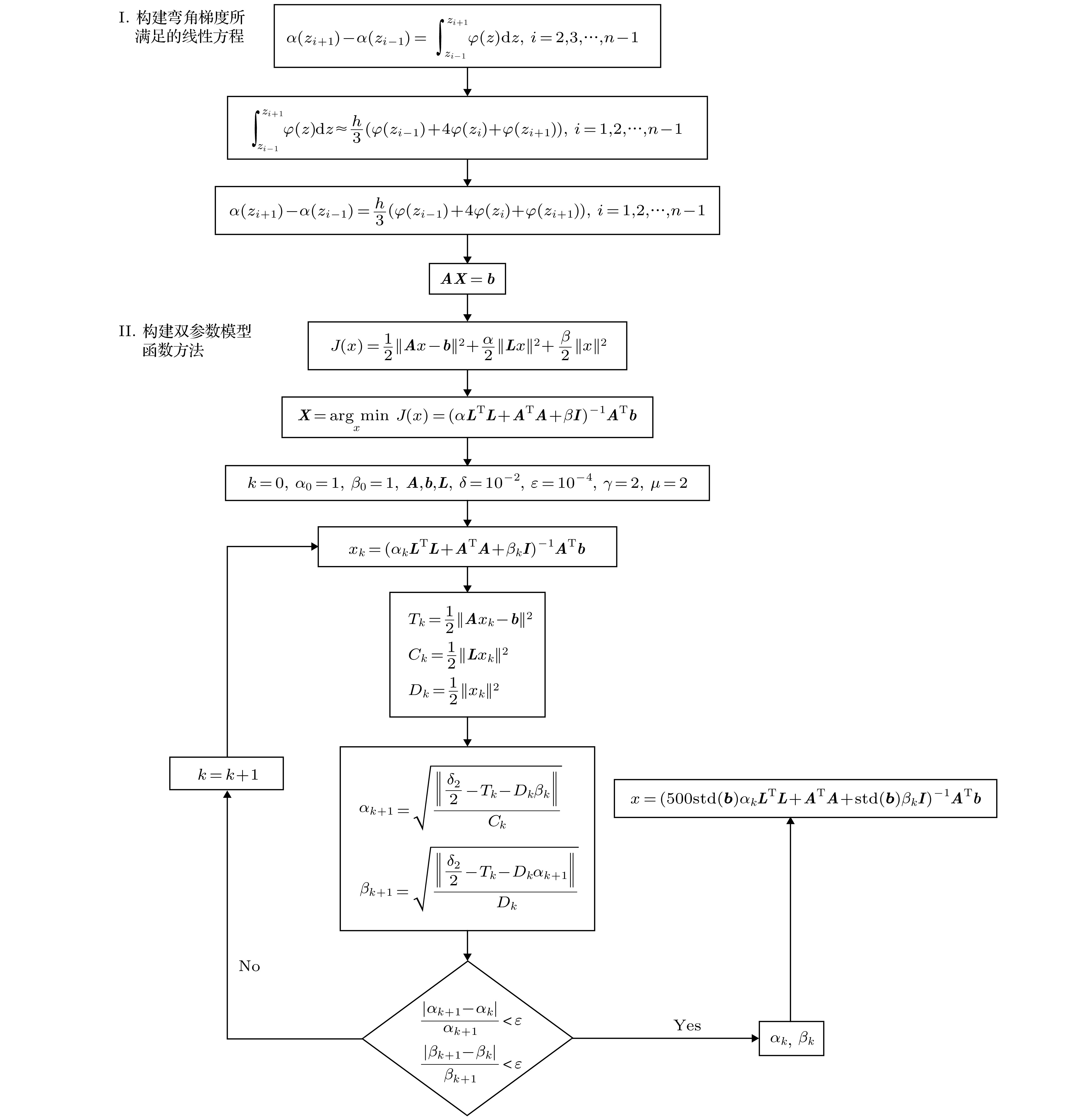
提出了一种确定大气边界层顶高度的数值微分新方法, 该方法使用了正则化技术, 把对弯角廓线求导数的数值微分问题转化为求目标泛函极小值的问题, 采用双参数模型函数方法来选择正则化参数, 最后利用最大梯度法确定边界层顶高度. 首先通过两个数值实验验证了新方法的有效性, 实验结果显示, 随着掩星资料噪音的增多, 由差分法和结合L曲线方案的数值微分方法得到的边界层顶高度波动增大, 而通过双参数模型函数方法得到的高度很稳定, 这说明新方法能够很好地过滤噪音, 从而保留廓线的主要信息. 随后基于2007—2011年1, 4, 7, 10月的COSMIC弯角数据, 利用新方法分析了全球海洋大气边界层顶高度的季节特征, 并与用掩星资料自带的大气边界层顶高度数据zbalmax得到的季节分布进行对比. 结果表明, 两者的季节分布特征十分一致: 海温相对周围海域高的区域, 边界层顶高度较高, 反之, 边界层顶高度较低; 在暖流经过的海域, 边界层顶高度较高, 在寒流经过的海域, 边界层顶的高度相对较低.

关键词:

Abstract

In this paper, we propose a new method of numerical differentiation to determine the height of the top layer of the atmospheric boundary layer. In this method, a regularization technique is used to convert the problem of calculating the differential of the curve of the corners into the problem of finding the minimum value of the objective function. The two-parameter model function method is used to select the regularization parameters. Finally, the maximum gradient method is used to determine the top height of the boundary layer. Firstly, the effectiveness of the new method is validated through two numerical experiments. The experimental results show that as the noise of the occultation data increases, the fluctuation of the height of the boundary layer top obtained by the difference method and the numerical differentiation method combined with the L curve scheme increases. And the height obtained by the two-parameter model function method is very stable, which shows that the new method can filter the noise well, thereby retaining the main information about the profile. Then, based on the COSMIC angle data in January, April, July and October 2007－2011, the new method is used to analyze the seasonal characteristics of the height of the global oceanic and atmospheric boundary layer, compared with the seasonal distribution obtained by “zbalmax” with the occultation data. The results show that the seasonal distribution characteristics of the two data are very consistent: the height of the boundary layer is higher in the area where the sea surface temperature is higher than that in the surrounding sea area; on the contrary, the height of the boundary layer top is lower. In the sea area where the warm current passes, the height of the boundary layer is higher; in the sea area where the cold current passes, the height of the boundary layer is lower.

Keywords:

作者及机构信息

1.
国防科技大学气象海洋学院, 南京　211101

2.
国家海洋局第二海洋研究所, 卫星海洋环境动力学国家重点实验室, 杭州　310012

通信作者: 黄思训, huangsxp@163.com

基金项目: 国家级-国家自然科学基金(91730304)

Authors and contacts

1.
College of Meteorology and Oceanography, National University of Defense Technology, Nanjing 211101, China

2.
State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, State Oceanic Administration, Hangzhou 310012, China

Corresponding author: Huang Si-Xun, huangsxp@163.com

文章全文 : translate this paragraph

参考文献

[1]	Stull R B 1999 An Introduction to Boundary Layer Meteorology (Vol. 13) (Dordrecht: Kluwer Academic Publishers) pp3, 4
[2]	Seibert P, Beyrich F, Gryning S E, Joffre S, Rasmussen A, Tercier P 2000 Atmos. Environ. 34 1001 Google Scholar
[3]	Zeng X, Brunke M A, Zhou M, Fairall C, Bond N A, Lenschow D H 2004 J. Clim. 17 4159 Google Scholar
[4]	Chan K M, Wood R 2013 J. Geophys. Res. Atmos. 118 12 Google Scholar
[5]	Ho S P, Peng L, Anthes R A, Kuo Y H, Lin H C 2015 J. Clim. 28 2856 Google Scholar
[6]	Holzworth G C 1964 Mon. Weather Rev. 92 235 Google Scholar
[7]	Coulter R L 1979 J. Appl. Meteorol. Climatol. 18 1495 Google Scholar
[8]	Van Pul W A J, Holtslag A A M, Swart D P J 1994 Bound.-Layer Meteorol. 68 173 Google Scholar
[9]	Bianco L, Wilczak J M 2002 J. Atmos. Oceanic Technol. 19 1745 Google Scholar
[10]	Lokoshchenko M A 2002 J. Atmos. Oceanic Technol. 19 1151 Google Scholar
[11]	Balsley B B, Frehlich R G, Jensen M L, Meillier Y 2006 J. Atmos. Sci. 63 1291 Google Scholar
[12]	Sokolovskiy S, Kuo Y H, Rocken C, Schreiner W S, Hunt D, Anthes R A 2006 Geophys. Res. Lett. 33 12 Google Scholar
[13]	Sokolovskiy S V, Rocken C, Lenschow D H, Kuo Y H, Anthes R A, Schreiner W S, Hunt D C 2007 Geophys. Res. Lett. 34 18 Google Scholar
[14]	Baars H, Ansmann A, Engelmann R, Althausen D 2008 Atmos. Chem. Phys. 8 7281 Google Scholar
[15]	Seidel D J, Ao C O, Li K 2010 J. Geophys. Res. Atmos. 115 16 Google Scholar
[16]	Dai C, Wang Q, Kalogiros J A, Lenschow D H, Gao Z, Zhou M 2014 Bound.-Layer Meteorol. 152 277 Google Scholar
[17]	Yan S, Xiang J, Du H 2019 Adv. Atmos. Sci. 36 303 Google Scholar
[18]	Tikhonov A N 1963 Dokl. Akad. Nauk SSSR 151
[19]	Willoughby R A 1979 SIAM Rev. Soc. Ind. Appl. Math. 21 266 Google Scholar
[20]	Tautenhahn U 2002 Inverse Prob. 18 191 Google Scholar
[21]	张路寅 2011 硕士学位论文 (济南: 山东大学) Zhang L Y 2011 M.S. Thesis (Jinan: Shandong University) (in Chinese)
[22]	Hanke M, Neubauer A, Scherzer O 1995 Numer. Math. 72 21 Google Scholar
[23]	Shirangi M G, Emerick A A 2016 J. Pet. Sci. Eng. 143 258 Google Scholar
[24]	姜祝辉, 黄思训, 何然, 周晨腾 2011 60 068401 Google Scholar Jiang Z H, Huang S X, He R, Zhou C T 2011 Acta Phys. Sin. 60 068401 Google Scholar
[25]	赵延来, 黄思训, 杜华栋, 仲跻芹 2011 60 079202 Google Scholar Zhao Y L, Huang S X, Du H D, Zhong Q Q 2011 Acta Phys. Sin. 60 079202 Google Scholar
[26]	Zhang L, Huang S X, Shen C, Shi W L 2011 Chin. Phys. B 20 514 Google Scholar
[27]	Zhong J, Huang S X, Fei J F, Du H D, Zhang L 2011 Chin. Phys. B 20 064301 Google Scholar
[28]	谢正超, 王飞, 严建华, 岑可法 2015 64 240201 Google Scholar Xie Z C, Wang F, Yan J H, Ling K F 2015 Acta Phys. Sin. 64 240201 Google Scholar
[29]	Hansen P C 1992 SIAM Rev. Soc. Ind. Appl. Math. 34 561 Google Scholar
[30]	Hansen P C 1994 Numer. Algorithms 6 1 Google Scholar
[31]	黄威, 刘磊, 高太长, 李书磊, 胡帅 2016 光谱学与光谱分析 36 3620 Google Scholar Huang w, Liu L, Gao T C, Li S L, Hu S 2016 Spectrosc. Spect. Anal. 36 3620 Google Scholar
[32]	Golub G H, Heath M, Wahba G 1979 Technometrics 21 215 Google Scholar
[33]	Wen Y-W, Chan R H 2018 Inverse Prob. Imag. 12 1103 Google Scholar
[34]	Scherzer O 1993 Computing 51 45 Google Scholar
[35]	Morozov V A 1984 Methods for Solving Incorrectly Posed Problems (New York: Springer-Verlag) pp65−70
[36]	Kunisch K, Zou J 1998 Inverse Prob. 14 1247 Google Scholar
[37]	Lu S, Pereverzev S V 2011 Numer. Math. 118 1 Google Scholar
[38]	王泽文 2010 博士学位论文 (南京: 东南大学) Wang Z W 2010 Ph. D. Dissertation (Nanjing: Southeast University) (in Chinese)
[39]	刘继军 2005 不适定问题的正则化方法及应用 (北京: 科学出版社) 第83−89页 Liu J J 2005 Regularization Method and Application of Ill-posed Problems (Beijing: Science Press) pp83−89 (in Chinese)
[40]	汪代维, 杨修群 2002 气象学报 02 129 Google Scholar Wang D W, Yang X Q 2002 Acta Meteorol. Sin. 02 129 Google Scholar

施引文献

图 1 2007−2011年1, 4, 7, 10月份掩星廓线数量的时间分布

Fig. 1. Temporal distribution of the number of occultation profiles in January, April, July and October, 2007−2011.

下载: 全尺寸图片幻灯片

图 2 双参数模型函数法流程图

Fig. 2. Flow chart of two-parameter model function method.

下载: 全尺寸图片幻灯片

图 3 由差分法和模型函数法得到的弯角梯度廓线(BA表示弯角)　(a)弯角廓线添加随机误差$\delta = 0.0025$, 边界层顶高度${H_{\rm{M}}} = 1.2\;{\rm{km}}, {H_{\rm{d}}} = 1.4\;{\rm{km}}$; (b)弯角廓线添加随机误差$\delta = 0.005$, 边界层顶高度${H_{\rm{M}}} = 1.1\;{\rm{km}}, {H_{\rm{d}}} = 1.4\;{\rm{km}}$; (c)弯角廓线添加随机误差$\delta = 0.0075$, 边界层顶高度${H_{\rm{M}}} = 1.2\;{\rm{km}}, {H_{\rm{d}}} = 1.8\;{\rm{km}}$; (d)弯角廓线添加随机误差$\delta = 0.01$, 边界层顶高度H_M = 1.2 km, H_d = 3.7 km

Fig. 3. Angle gradient profile obtained by the difference method and the model function method using the bending angle gradient profile (BA represents the bending angle): (a) Bending angle profile with uniform random error $\delta = 0.0025$, boundary layer top height ${H_{\rm{M}}} = 1.2\;{\rm{km}}, {H_{\rm{d}}} = 1.4\;{\rm{km}}$; (b) bending angle profile with uniform random error $\delta = 0.005$, boundary layer top height ${H_{\rm{M}}} = 1.1\;{\rm{km}}, {H_{\rm{d}}} = 1.4\;{\rm{km}}$; (c) bending angle profile with uniform random error $\delta = 0.0075$, boundary layer top height ${H_{\rm{M}}} = 1.2\;{\rm{km}}, {H_{\rm{d}}} = 1.8\;{\rm{km}}$; (d) bending angle profile with uniform random error $\delta = 0.01$, boundary layer top height ${H_{\rm{M}}} = 1.2\;{\rm{km}}, {H_{\rm{d}}} = 3.7\;{\rm{km}}$.

下载: 全尺寸图片幻灯片

图 4 由差分法、L曲线法和模型函数法得到的边界层顶高度　(a) 三种方法基于廓线1得到的边界层顶高度, H_true = 3.15 km, std(H_M) = 0.013, std(H_L) = 0.44, std(H_M) = 0.61; (b) 三种方法基于廓线2得到的边界层顶高度, H_true = 4.55 km, std(H_M) = 0.020, std(H_L) = 0.89, std(H_M) = 1.19

Fig. 4. Height of the boundary layer obtained by the three methods: (a) Three methods to get the height of the boundary layer top based on profile 1, H_true = 3.15 km, std(H_M) = 0.013, std(H_L) = 0.44, std(H_M) = 0.61; (b) three methods to get the height of the boundary layer top based on profile 2, H_true = 4.55 km, std(H_M) = 0.020, std(H_L) = 0.89, std(H_M) = 1.19

下载: 全尺寸图片幻灯片

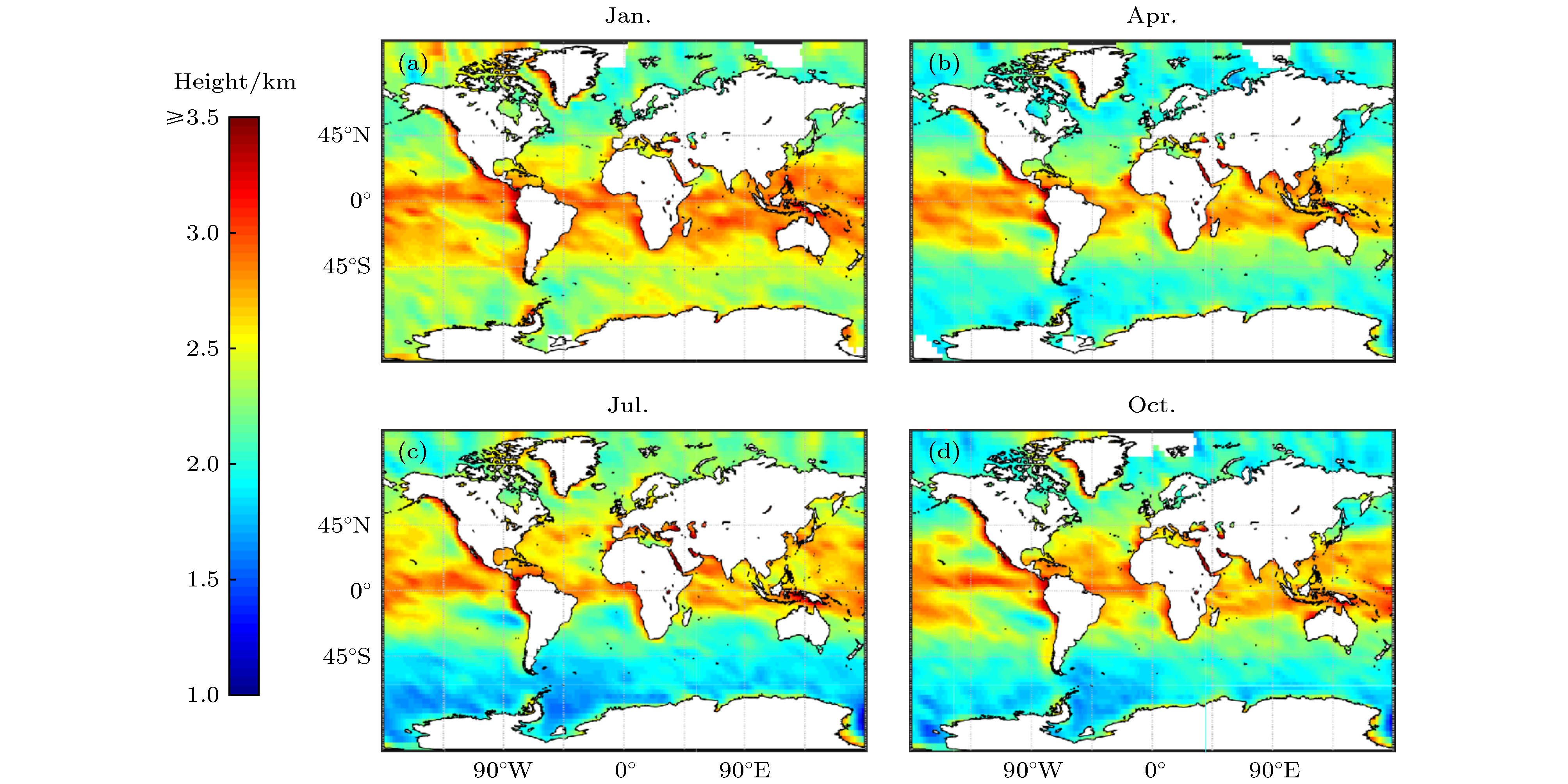
图 5 用模型函数法得到的海洋5年平均的边界层顶高度(所用资料为2007—2011年1, 4, 7, 10四个月份的掩星弯角的资料)　(a) 1月份平均边界层顶高度; (b) 4月份平均边界层顶高度; (c) 7月份平均边界层顶高度; (d) 10月份平均边界层顶高度

Fig. 5. The 5-year average boundary layer height of the ocean obtained by the model function method, the data used is the bending angle profile of the four months of 2007−2011 in January, April, July, and October: (a) The average height of the boundary layer in January; (b) the average height of the boundary layer in April; (c) the average height of the boundary layer in July; (d) the average height of the boundary layer in October.

下载: 全尺寸图片幻灯片

图 6 海洋5年平均的边界层顶高度(所用资料为2007—2011年1, 4, 7, 10四个月份的掩星自带zbalmax的资料)　(a) 1月份平均边界层顶高度; (b) 4月份平均边界层顶高度; (c) 7月份平均边界层顶高度; (d) 10月份平均边界层顶高度

Fig. 6. The 5-year average boundary layer height of the ocean obtained by the model function method, the data used is the zbalmax provided by CDAAC of the four months of 2007−2011 in January, April, July, and October: (a) The average height of the boundary layer in January; (b) the average height of the boundary layer in April; (c) the average height of the boundary layer in July; (d) the average height of the boundary layer in October.

下载: 全尺寸图片幻灯片

map

[1]	Stull R B 1999 An Introduction to Boundary Layer Meteorology (Vol. 13) (Dordrecht: Kluwer Academic Publishers) pp3, 4
[2]	Seibert P, Beyrich F, Gryning S E, Joffre S, Rasmussen A, Tercier P 2000 Atmos. Environ. 34 1001 Google Scholar
[3]	Zeng X, Brunke M A, Zhou M, Fairall C, Bond N A, Lenschow D H 2004 J. Clim. 17 4159 Google Scholar
[4]	Chan K M, Wood R 2013 J. Geophys. Res. Atmos. 118 12 Google Scholar
[5]	Ho S P, Peng L, Anthes R A, Kuo Y H, Lin H C 2015 J. Clim. 28 2856 Google Scholar
[6]	Holzworth G C 1964 Mon. Weather Rev. 92 235 Google Scholar
[7]	Coulter R L 1979 J. Appl. Meteorol. Climatol. 18 1495 Google Scholar
[8]	Van Pul W A J, Holtslag A A M, Swart D P J 1994 Bound.-Layer Meteorol. 68 173 Google Scholar
[9]	Bianco L, Wilczak J M 2002 J. Atmos. Oceanic Technol. 19 1745 Google Scholar
[10]	Lokoshchenko M A 2002 J. Atmos. Oceanic Technol. 19 1151 Google Scholar
[11]	Balsley B B, Frehlich R G, Jensen M L, Meillier Y 2006 J. Atmos. Sci. 63 1291 Google Scholar
[12]	Sokolovskiy S, Kuo Y H, Rocken C, Schreiner W S, Hunt D, Anthes R A 2006 Geophys. Res. Lett. 33 12 Google Scholar
[13]	Sokolovskiy S V, Rocken C, Lenschow D H, Kuo Y H, Anthes R A, Schreiner W S, Hunt D C 2007 Geophys. Res. Lett. 34 18 Google Scholar
[14]	Baars H, Ansmann A, Engelmann R, Althausen D 2008 Atmos. Chem. Phys. 8 7281 Google Scholar
[15]	Seidel D J, Ao C O, Li K 2010 J. Geophys. Res. Atmos. 115 16 Google Scholar
[16]	Dai C, Wang Q, Kalogiros J A, Lenschow D H, Gao Z, Zhou M 2014 Bound.-Layer Meteorol. 152 277 Google Scholar
[17]	Yan S, Xiang J, Du H 2019 Adv. Atmos. Sci. 36 303 Google Scholar
[18]	Tikhonov A N 1963 Dokl. Akad. Nauk SSSR 151
[19]	Willoughby R A 1979 SIAM Rev. Soc. Ind. Appl. Math. 21 266 Google Scholar
[20]	Tautenhahn U 2002 Inverse Prob. 18 191 Google Scholar
[21]	张路寅 2011 硕士学位论文 (济南: 山东大学) Zhang L Y 2011 M.S. Thesis (Jinan: Shandong University) (in Chinese)
[22]	Hanke M, Neubauer A, Scherzer O 1995 Numer. Math. 72 21 Google Scholar
[23]	Shirangi M G, Emerick A A 2016 J. Pet. Sci. Eng. 143 258 Google Scholar
[24]	姜祝辉, 黄思训, 何然, 周晨腾 2011 60 068401 Google Scholar Jiang Z H, Huang S X, He R, Zhou C T 2011 Acta Phys. Sin. 60 068401 Google Scholar
[25]	赵延来, 黄思训, 杜华栋, 仲跻芹 2011 60 079202 Google Scholar Zhao Y L, Huang S X, Du H D, Zhong Q Q 2011 Acta Phys. Sin. 60 079202 Google Scholar
[26]	Zhang L, Huang S X, Shen C, Shi W L 2011 Chin. Phys. B 20 514 Google Scholar
[27]	Zhong J, Huang S X, Fei J F, Du H D, Zhang L 2011 Chin. Phys. B 20 064301 Google Scholar
[28]	谢正超, 王飞, 严建华, 岑可法 2015 64 240201 Google Scholar Xie Z C, Wang F, Yan J H, Ling K F 2015 Acta Phys. Sin. 64 240201 Google Scholar
[29]	Hansen P C 1992 SIAM Rev. Soc. Ind. Appl. Math. 34 561 Google Scholar
[30]	Hansen P C 1994 Numer. Algorithms 6 1 Google Scholar
[31]	黄威, 刘磊, 高太长, 李书磊, 胡帅 2016 光谱学与光谱分析 36 3620 Google Scholar Huang w, Liu L, Gao T C, Li S L, Hu S 2016 Spectrosc. Spect. Anal. 36 3620 Google Scholar
[32]	Golub G H, Heath M, Wahba G 1979 Technometrics 21 215 Google Scholar
[33]	Wen Y-W, Chan R H 2018 Inverse Prob. Imag. 12 1103 Google Scholar
[34]	Scherzer O 1993 Computing 51 45 Google Scholar
[35]	Morozov V A 1984 Methods for Solving Incorrectly Posed Problems (New York: Springer-Verlag) pp65−70
[36]	Kunisch K, Zou J 1998 Inverse Prob. 14 1247 Google Scholar
[37]	Lu S, Pereverzev S V 2011 Numer. Math. 118 1 Google Scholar
[38]	王泽文 2010 博士学位论文 (南京: 东南大学) Wang Z W 2010 Ph. D. Dissertation (Nanjing: Southeast University) (in Chinese)
[39]	刘继军 2005 不适定问题的正则化方法及应用 (北京: 科学出版社) 第83−89页 Liu J J 2005 Regularization Method and Application of Ill-posed Problems (Beijing: Science Press) pp83−89 (in Chinese)
[40]	汪代维, 杨修群 2002 气象学报 02 129 Google Scholar Wang D W, Yang X Q 2002 Acta Meteorol. Sin. 02 129 Google Scholar

[1]	李宁, TuXin, 黄孝龙, 翁春生. 基于Tikhonov正则化参数矩阵的激光吸收光谱燃烧场二维重建光路设计方法. , 2020, 69(22): 227801. doi: 10.7498/aps.69.20201144
[2]	陆昌根, 沈露予, 朱晓清. 压力梯度对壁面局部吹吸边界层感受性的影响研究. , 2019, 68(22): 224701. doi: 10.7498/aps.68.20190684
[3]	颜冰, 黄思训, 冯径. 大气边界层模式中随机参数的反演与不确定性分析. , 2018, 67(19): 199201. doi: 10.7498/aps.67.20181014
[4]	石明珠, 许廷发, 梁炯, 李相民. 单幅模糊图像点扩散函数估计的梯度倒谱分析方法研究. , 2013, 62(17): 174204. doi: 10.7498/aps.62.174204
[5]	周树波, 袁艳, 苏丽娟. 基于双阈值Huber范数估计的图像正则化超分辨率算法. , 2013, 62(20): 200701. doi: 10.7498/aps.62.200701
[6]	何然, 黄思训, 周晨腾, 姜祝辉. 遗传算法结合正则化方法反演海洋大气波导. , 2012, 61(4): 049201. doi: 10.7498/aps.61.049201
[7]	何明元, 杜华栋, 龙智勇, 黄思训. 大气廓线参数反演中基于大气可反演指数的正则化参数选择方法. , 2012, 61(2): 024205. doi: 10.7498/aps.61.024205
[8]	陈林, 唐登斌, Chaoqun Liu. 转捩边界层中流向条纹的新特性. , 2011, 60(9): 094702. doi: 10.7498/aps.60.094702
[9]	赵延来, 黄思训, 杜华栋, 仲跻芹. 正则化方法同化多普勒天气雷达资料及对降雨预报的影响. , 2011, 60(7): 079202. doi: 10.7498/aps.60.079202
[10]	姜祝辉, 黄思训, 何然, 周晨腾. 合成孔径雷达资料反演海面风场的正则化方法研究. , 2011, 60(6): 068401. doi: 10.7498/aps.60.068401
[11]	盛峥, 黄思训. 变分伴随正则化方法从雷达回波反演海洋波导(Ⅱ):实际反演试验. , 2010, 59(6): 3912-3916. doi: 10.7498/aps.59.3912
[12]	盛峥, 黄思训. 变分伴随正则化方法从雷达回波反演海洋波导(Ⅰ):理论推导部分. , 2010, 59(3): 1734-1739. doi: 10.7498/aps.59.1734
[13]	姜祝辉, 黄思训, 杜华栋, 刘博. 利用变分结合正则化方法对高度计风速资料调整海面风场的研究. , 2010, 59(12): 8968-8977. doi: 10.7498/aps.59.8968
[14]	张亮, 黄思训, 刘宇迪, 钟剑. 变分同化结合广义变分最佳分析对微波散射计资料进行海面风场反演. , 2010, 59(4): 2889-2897. doi: 10.7498/aps.59.2889
[15]	李加庆, 陈进, 杨超, 贾文强. 波叠加声场重构精度的影响因素分析. , 2008, 57(7): 4258-4264. doi: 10.7498/aps.57.4258
[16]	于飞, 陈心昭, 李卫兵, 陈剑. 空间声场全息重建的波叠加方法研究. , 2004, 53(8): 2607-2613. doi: 10.7498/aps.53.2607
[17]	王延申. 开边界六顶角模型的边界关联函数. , 2003, 52(11): 2700-2705. doi: 10.7498/aps.52.2700
[18]	郑振华, 陈羽, 缪容之. BaTiO3半导体陶瓷从PTC特性向边界层电容效应过渡问题探讨——晶界势垒模型的应用. , 1996, 45(9): 1543-1550. doi: 10.7498/aps.45.1543
[19]	丁鄂江, 黄祖洽. Boltzmann方程的奇异扰动解法(Ⅲ)——边界层解. , 1985, 34(2): 213-224. doi: 10.7498/aps.34.213
[20]	林鸿荪. 片流边界层中气流及热转移. , 1954, 10(1): 71-88. doi: 10.7498/aps.10.71

计量

文章访问数: 9527
PDF下载量: 153
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

确定大气边界层顶高度的新方法及数值实验