-
High-order-harmonic generation (HHG) is a fundamental atomic and molecular process in strong laser fields and plays a crucial role in the development of ultrafast science and technology. The essential features in HHG, such as the above-threshold harmonic plateau and cutoffs, can be well understood by the semiclassical three-step model. The HHG cutoff occurs approximately at the energy $3.17{U_{\rm p}} + {I_{\rm p}}$ , where${I_{\rm p}}$ is the atomic ionization potential, and${U_{\rm p}}$ is the ponderomotive potential.In the past, most studies focused on the HHG above the ionization threshold, and the general pattern of the HHG spectrum can be qualitatively explained by means of the strong field approximation (SFA) and the quantum treatment of three-dimensional time-dependent Schr?dinger equation (TDSE). However, the SFA results in inadequate description for the process in the harmonic generation below the ionization threshold since it neglects the Coulomb potential and the detailed electronic structure of atoms. Recently, as a promising method to produce vacuum-ultraviolet frequency comb, the HHG in the near- and below-ionization threshold has been increased considerably. However, the dynamical origin of in these lower harmonics is less understood and largely unexplored. Here we perform an ab initio quantum study of the near- and below-threshold harmonic generation of hydrogen atom by means of the time-dependent generalized pseudospectral method. We study the intensity dependence of the harmonic spectra below the ionization threshold of hydrogen atom in the intense laser field. The high-order harmonic spectra are calculated by the Fourier transform of the atom induced dipole moment in the laser field. The below-threshold harmonic spectra yield is scaled as a function of the laser peak intensity. We find that the spectra yield in below-threshold harmonic generation (BTHG) dependents on the light intensity in the multiphoton ionization regime. And the laser intensity plays an important role in the channel selection process for BTHG. There are mainly two kinds of quantum channels to be responsible for the BTHG. Namely, the generalized short trajectories and the long trajectories, in which the long trajectories are more sensitive to the laser field intensity. Combining with wavelet time-frequency transform, semiclassical trajectories simulation, and quantum channel analysis associated with the laser intensity, the dynamical origin of the BTHG is uncovered. -
Keywords:
- intense laser field /
- below-threshold harmonic generation /
- ionization threshold /
- quantum channel
[1] McPherson A, Gibson G, Jara H, Johann U, Luk T S, McIntyre I A, Boyer K, Rhodes C K 1987 J. Opt. Soc. Am. B. 4 595
Google Scholar
[2] Ferray M, L’Huillier A, Li X F, Lompre L A, Mainfray G, Manus C 1988 J. Phys. B: At. Mol. Opt. Phys. 21 31
Google Scholar
[3] Brabec T, Krausz F 2000 Rev. Mod. Phys. 72 545
Google Scholar
[4] Takahashi E J, Kanai T, Ishikawa K L, Nabekawa Y, Midorikawa K 2008 Phys. Rev. Lett. 101 253901
Google Scholar
[5] Budil K S, Salières P, L’Huillier A, Ditmire T, Perry M D 1993 Phys. Rev. A. 48 3437
Google Scholar
[6] Chini M, Zhao K, Chang Z H 2014 Nat. Photonics. 8 178
Google Scholar
[7] Wang L, Wang G L, Jiao Z H, Zhao S F, Zhou X X 2018 Chin. Phys. B. 27 073205
Google Scholar
[8] Li P C, Jiao Y X, Zhou X X, Chu S I 2016 Optics. Express. 24 14352
Google Scholar
[9] Frolov M V, Manakov N L, Sarantseva T S, Emelin M Y, Ryabikin M Y, Starace A F 2009 Phys. Rev. Lett. 102 243901
Google Scholar
[10] Dao L V, Dinh K B, Hannaford P 2013 Appl. Phys. Lett. 103 141115
Google Scholar
[11] Grazioli C, Callegari C, Ciavardini A, Coreno M, Frassetto F, Gauthier D, Golob D, Ivanov R, Kivimäki A, Mahieu B, Bučar B, Merhar M, Miotti P, Poletto L, Polo E, Ressel B, Spezzani C, De N G 2014 Rev. Sci. Instrum. 85 023104
Google Scholar
[12] Wang G L, Jin C, Le A T, Lin C D 2012 Phys. Rev. A. 86 015401
Google Scholar
[13] Dinh K B, Le H V, Hannaford P, Dao L V 2015 Appl. Opt. 54 5303
Google Scholar
[14] Xiong W H, Geng J W, Tang J Y, Peng L Y, Gong Q H 2014 Phys. Rev. Lett. 112 233001
Google Scholar
[15] Spott A, Becker A, Jaroń-Becker A 2015 Phys. Rev. A. 91 023402
Google Scholar
[16] Chini M, Wang X W, Cheng Y, Wang H, Wu Y, Cunningham E, Li P C, Hesla J A, Telnov D, Chu S I, Chang Z H 2014 Nat. Photonics. 10 1038
[17] Xiong W H, Gong Q H, Peng L Y 2017 Phys. Rev. A. 96 023421
Google Scholar
[18] Heslar J, Chu S I 2017 Phys. Rev. A. 95 043414
Google Scholar
[19] Du L L, Wang G L, Li P C, Zhou X X 2018 Chin. Phys. B. 27 113201
Google Scholar
[20] Xiong W H, Peng L Y, Gong Q H 2017 J. Phys. B 50 032001
Google Scholar
[21] Corkum P B 1993 Phys. Rev. Lett. 71 1994
Google Scholar
[22] Lewenstein M, Balcou P, Ivanov M Y, L’Huillier A, Corkum P B 1994 Phys. Rev. A 49 2117
Google Scholar
[23] Yost D C, Schibli T R, Ye J, Tate J L, Hostetter J, Gaarde M B, Schafer K J 2009 Nat. Phys. 10 1038
[24] Power E P, March A M, Catoire F, Sistrunk E, Krushelnick K, Agostini P, DiMauro L F 2010 Nat. Photonics. 4 352
Google Scholar
[25] Soifer H, Botheron P, Shafir D, Diner A, Raz O, Bruner B D, Mairesse Y, Pons B, Dudovich N 2010 Phys. Rev. Lett. 105 143904
Google Scholar
[26] Hostetter J A, Tate J L, Schafer K J, Gaarde M B 2010 Phys. Rev. A 82 023401
Google Scholar
[27] He L X, Lan P F, Zhai C Y, Li Y, Wang Z, Zhang Q B, Lu P X 2015 Phys. Rev. A. 91 023428
Google Scholar
[28] Beaulieu S, Camp S, Descamps D, Comby A, Wanie V, Petit S, Légaré F, Schafer K J, Gaarde M B, Catoire F, Mairesse Y 2016 Phys. Rev. Lett. 117 203001
Google Scholar
[29] Li P C, Sheu Y L, Laughlin C, Chu S I 2014 Phys. Rev. A. 90 041401
Google Scholar
[30] Tong X M, Chu S I 1997 Chem. Phys. 217 119
Google Scholar
[31] Balcou P, Dederichs A S, Gaarde M B, L’Huillier A 1999 J. Phys. B. 32 2973
Google Scholar
[32] Keldysh L V 1965 Sov. Phys. JETP. 20 1307
[33] Chu X, Chu S I 2010 Phys. Rev. A. 64 013406
Google Scholar
[34] Li P C, Sheu Y L, Jooya H Z, Zhou X X, Chu S I 2016 Sci. Reports. 6 32763
Google Scholar
-
图 1 H原子产生的低于电离阈值的高次谐波谱 (a)波长为
$800{\rm{~nm}}$ , 强度为I = 6.0 × 1013 W/cm2 (黑色实线), I = 1.0 × 1014 W/cm2 (红色实线), 以及I = 1.4 × 1014 W/cm2 (绿色实线), 蓝色线表示H原子的电离能${I_{\rm p}}$ ; (b)同(a)图, 波长为$1600\;{\rm{ nm}}$ 的情况Fig. 1. The HHG spectra produced by the hydrogen atom below the ionization threshold: (a) The wavelength is
$800\;{\rm{ nm}}$ , and the intensity is$I = 6.0 \times {10^{13}}\;{\rm{ W/c}}{{\rm{m}}^{\rm{2}}}$ (black solid line),$I = 1.0 \times {10^{14}}\;{\rm{ W/c}}{{\rm{m}}^{\rm{2}}}$ (red solid line), and$I = 1.4 \times {10^{14}}\;{\rm{ W/c}}{{\rm{m}}^{\rm{2}}}$ (green solid line), the blue lines indicate the ionization energy Ip of hydrogen atom; (b) same as (a), the wavelength is$1600\;{\rm{ nm}}$ case.
图 2 低于电离阈值的H5(黑色实线), H7(红线), 和H9(蓝色实线)的峰值强度随激光场强度的变化. 这里, 波长取为
$800\;{\rm{ nm}}$ , 其它激光场参数同图1(a). 箭头a, b, c, d分别表示在激光强度$I$ 为$3.1 \times {10^{13}}{\rm{ }}$ ,$3.6 \times {10^{13}}$ ,$4.3 \times {10^{13}}$ , 和$6.6 \times {10^{13}}$ ${\rm{W/c}}{{\rm{m}}^{\rm{2}}}$ 时H9的峰值强度Fig. 2. The peak intensity of H5(black solid line), H7(red line), and H9 (blue solid line) below the ionization threshold as a function of the laser field intensity. Here, the wavelength is
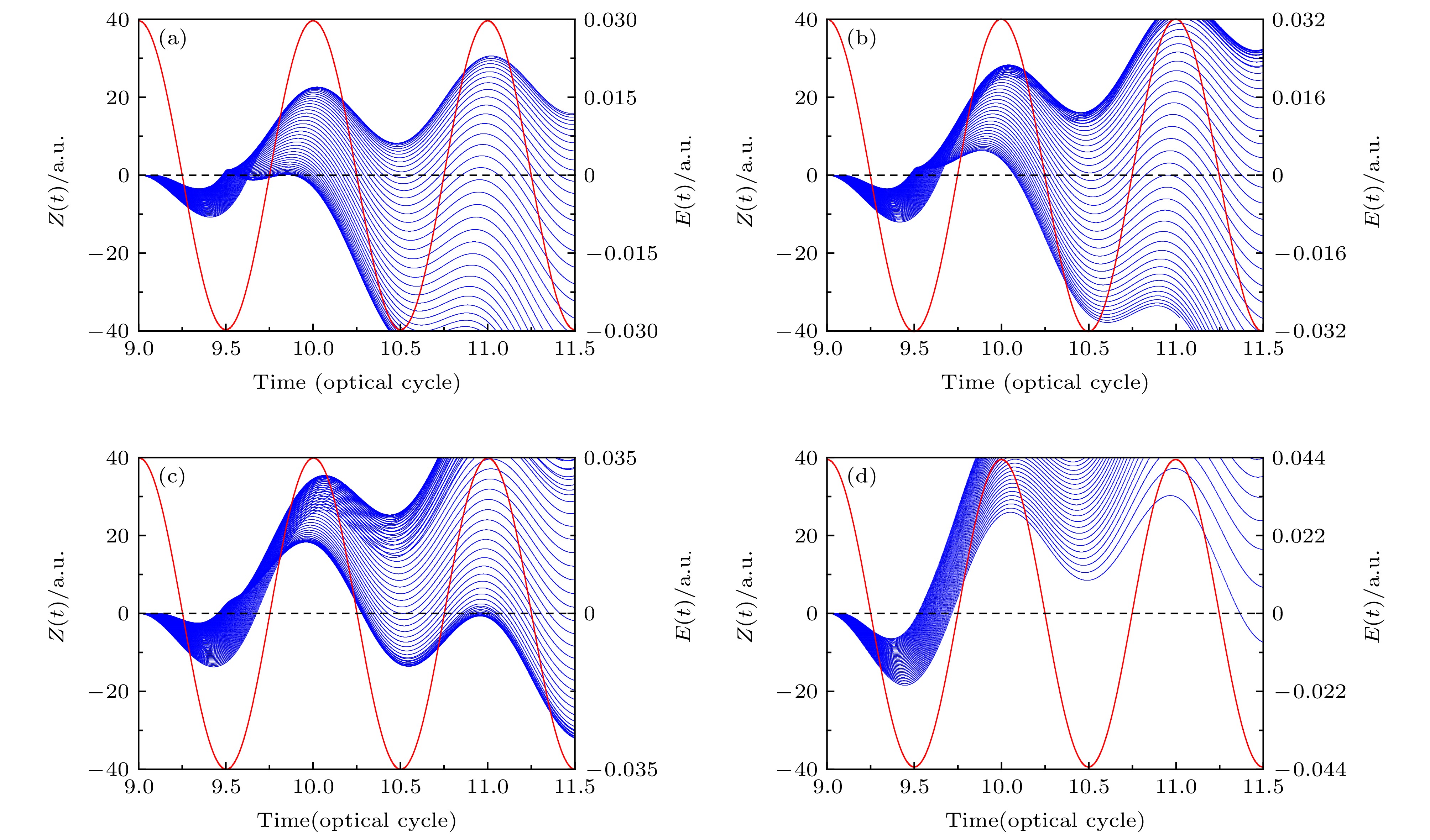
$800\;{\rm{ nm}}$ , and the other laser field parameters used are the same as those in Fig. 1(a). The arrows a, b, c, and d indicate the peak intensity of H9 at the intensity$I$ of$3.1 \times {10^{13}}{\rm{ }}$ ,$3.6 \times {10^{13}}$ ,$4.3 \times {10^{13}}$ ${\rm{W/c}}{{\rm{m}}^{\rm{2}}}$ , and 6.6 ×$ {10^{13}}$ ${\rm{W/c}}{{\rm{m}}^{\rm{2}}}$ , respectively.
图 3 H9曲线上a, b, c, d四个特殊点处对应的电子动力学轨迹, 红色实线代表激光场, 蓝色实线表示电子的轨迹, 黑色虚线表示母核位置. 激光场参数同图2
Fig. 3. The time-dependent position of electrons at the given laser intensity shown in a, b, c, and d points in H9 curve. The red solid lines represent the laser field, the blue solid lines represent the trajectories of the electron, and the black dotted lines represent the position of the parent nucleus. The other laser field parameters used are the same as those in Fig. 2.
图 4 波长为
$800\;{\rm{ nm}}$ 激光脉冲下, 低于电离阈值谐波的时频分析 (a)$I = 3.1 \times {10^{13}}\;{\rm{ W/c}}{{\rm{m}}^{\rm{2}}}$ ; (b)$I = 3.6 \times {10^{13}}\;{\rm{ W/c}}{{\rm{m}}^{\rm{2}}}$ ; (c)$I = 4.3 \times {10^{13}}\;{\rm{ W/c}}{{\rm{m}}^{\rm{2}}}$ ; (d)$I = 6.6 \times {10^{13}}\;{\rm{ W/c}}{{\rm{m}}^{\rm{2}}}$ Fig. 4. Time-frequency analysis of below-threshold harmonic generation with a
$800\;{\rm{ nm}}$ wavelength: (a)$I = 3.1 \times {10^{13}}\;{\rm{ W/c}}{{\rm{m}}^{\rm{2}}}$ ; (b)$I = 3.6 \times {10^{13}}\;{\rm{ W/c}}{{\rm{m}}^{\rm{2}}}$ ; (c)$I = 4.3 \times {10^{13}}\;{\rm{ W/c}}{{\rm{m}}^{\rm{2}}}$ ; (d)$I = 6.6 \times {10^{13}}\;{\rm{ W/c}}{{\rm{m}}^{\rm{2}}}$ .
图 5 波长为
$800\;{\rm{ nm}}$ , 强度为$I = 6.6 \times {10^{13}}\;{\rm{ W/c}}{{\rm{m}}^{\rm{2}}}$ 激光脉冲下, 低于电离阈值的时频分析 (a) H5; (b) H7; (c) H9Fig. 5. Time-frequency analysis of below-threshold harmonic, in a
$800\;{\rm{ nm}}$ laser wavelength with the intensity$I = 6.6 \times {10^{13}}\;{\rm{ W/c}}{{\rm{m}}^{\rm{2}}}$ : (a) H5; (b) H7; (c) H9.
-
[1] McPherson A, Gibson G, Jara H, Johann U, Luk T S, McIntyre I A, Boyer K, Rhodes C K 1987 J. Opt. Soc. Am. B. 4 595
Google Scholar
[2] Ferray M, L’Huillier A, Li X F, Lompre L A, Mainfray G, Manus C 1988 J. Phys. B: At. Mol. Opt. Phys. 21 31
Google Scholar
[3] Brabec T, Krausz F 2000 Rev. Mod. Phys. 72 545
Google Scholar
[4] Takahashi E J, Kanai T, Ishikawa K L, Nabekawa Y, Midorikawa K 2008 Phys. Rev. Lett. 101 253901
Google Scholar
[5] Budil K S, Salières P, L’Huillier A, Ditmire T, Perry M D 1993 Phys. Rev. A. 48 3437
Google Scholar
[6] Chini M, Zhao K, Chang Z H 2014 Nat. Photonics. 8 178
Google Scholar
[7] Wang L, Wang G L, Jiao Z H, Zhao S F, Zhou X X 2018 Chin. Phys. B. 27 073205
Google Scholar
[8] Li P C, Jiao Y X, Zhou X X, Chu S I 2016 Optics. Express. 24 14352
Google Scholar
[9] Frolov M V, Manakov N L, Sarantseva T S, Emelin M Y, Ryabikin M Y, Starace A F 2009 Phys. Rev. Lett. 102 243901
Google Scholar
[10] Dao L V, Dinh K B, Hannaford P 2013 Appl. Phys. Lett. 103 141115
Google Scholar
[11] Grazioli C, Callegari C, Ciavardini A, Coreno M, Frassetto F, Gauthier D, Golob D, Ivanov R, Kivimäki A, Mahieu B, Bučar B, Merhar M, Miotti P, Poletto L, Polo E, Ressel B, Spezzani C, De N G 2014 Rev. Sci. Instrum. 85 023104
Google Scholar
[12] Wang G L, Jin C, Le A T, Lin C D 2012 Phys. Rev. A. 86 015401
Google Scholar
[13] Dinh K B, Le H V, Hannaford P, Dao L V 2015 Appl. Opt. 54 5303
Google Scholar
[14] Xiong W H, Geng J W, Tang J Y, Peng L Y, Gong Q H 2014 Phys. Rev. Lett. 112 233001
Google Scholar
[15] Spott A, Becker A, Jaroń-Becker A 2015 Phys. Rev. A. 91 023402
Google Scholar
[16] Chini M, Wang X W, Cheng Y, Wang H, Wu Y, Cunningham E, Li P C, Hesla J A, Telnov D, Chu S I, Chang Z H 2014 Nat. Photonics. 10 1038
[17] Xiong W H, Gong Q H, Peng L Y 2017 Phys. Rev. A. 96 023421
Google Scholar
[18] Heslar J, Chu S I 2017 Phys. Rev. A. 95 043414
Google Scholar
[19] Du L L, Wang G L, Li P C, Zhou X X 2018 Chin. Phys. B. 27 113201
Google Scholar
[20] Xiong W H, Peng L Y, Gong Q H 2017 J. Phys. B 50 032001
Google Scholar
[21] Corkum P B 1993 Phys. Rev. Lett. 71 1994
Google Scholar
[22] Lewenstein M, Balcou P, Ivanov M Y, L’Huillier A, Corkum P B 1994 Phys. Rev. A 49 2117
Google Scholar
[23] Yost D C, Schibli T R, Ye J, Tate J L, Hostetter J, Gaarde M B, Schafer K J 2009 Nat. Phys. 10 1038
[24] Power E P, March A M, Catoire F, Sistrunk E, Krushelnick K, Agostini P, DiMauro L F 2010 Nat. Photonics. 4 352
Google Scholar
[25] Soifer H, Botheron P, Shafir D, Diner A, Raz O, Bruner B D, Mairesse Y, Pons B, Dudovich N 2010 Phys. Rev. Lett. 105 143904
Google Scholar
[26] Hostetter J A, Tate J L, Schafer K J, Gaarde M B 2010 Phys. Rev. A 82 023401
Google Scholar
[27] He L X, Lan P F, Zhai C Y, Li Y, Wang Z, Zhang Q B, Lu P X 2015 Phys. Rev. A. 91 023428
Google Scholar
[28] Beaulieu S, Camp S, Descamps D, Comby A, Wanie V, Petit S, Légaré F, Schafer K J, Gaarde M B, Catoire F, Mairesse Y 2016 Phys. Rev. Lett. 117 203001
Google Scholar
[29] Li P C, Sheu Y L, Laughlin C, Chu S I 2014 Phys. Rev. A. 90 041401
Google Scholar
[30] Tong X M, Chu S I 1997 Chem. Phys. 217 119
Google Scholar
[31] Balcou P, Dederichs A S, Gaarde M B, L’Huillier A 1999 J. Phys. B. 32 2973
Google Scholar
[32] Keldysh L V 1965 Sov. Phys. JETP. 20 1307
[33] Chu X, Chu S I 2010 Phys. Rev. A. 64 013406
Google Scholar
[34] Li P C, Sheu Y L, Jooya H Z, Zhou X X, Chu S I 2016 Sci. Reports. 6 32763
Google Scholar
下载:
计量
- 文章访问数: 9712
- PDF下载量: 685
- 被引次数: 0
