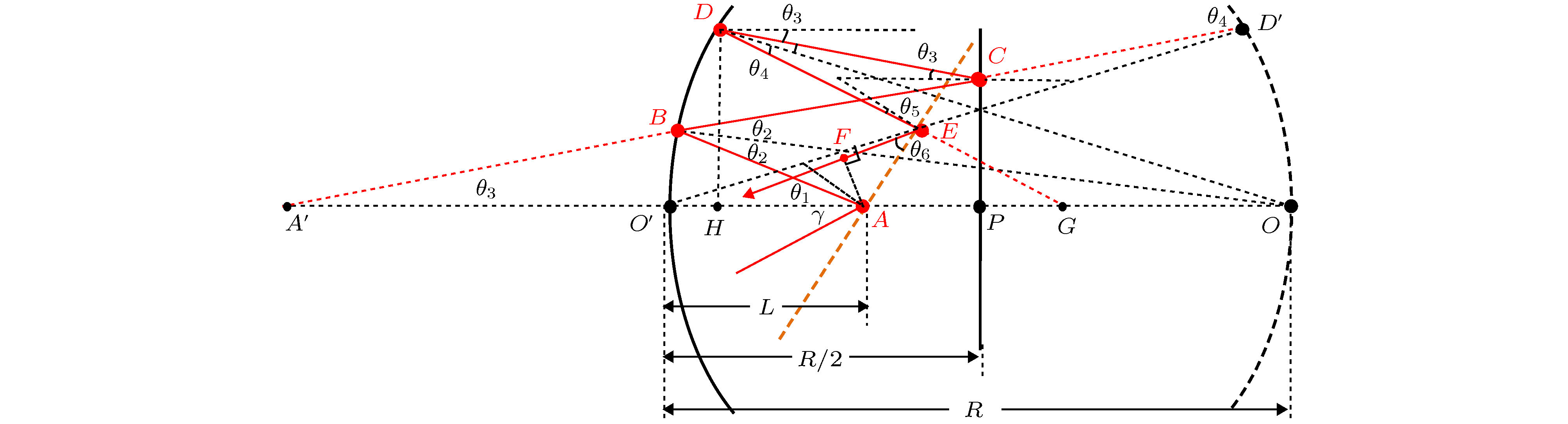
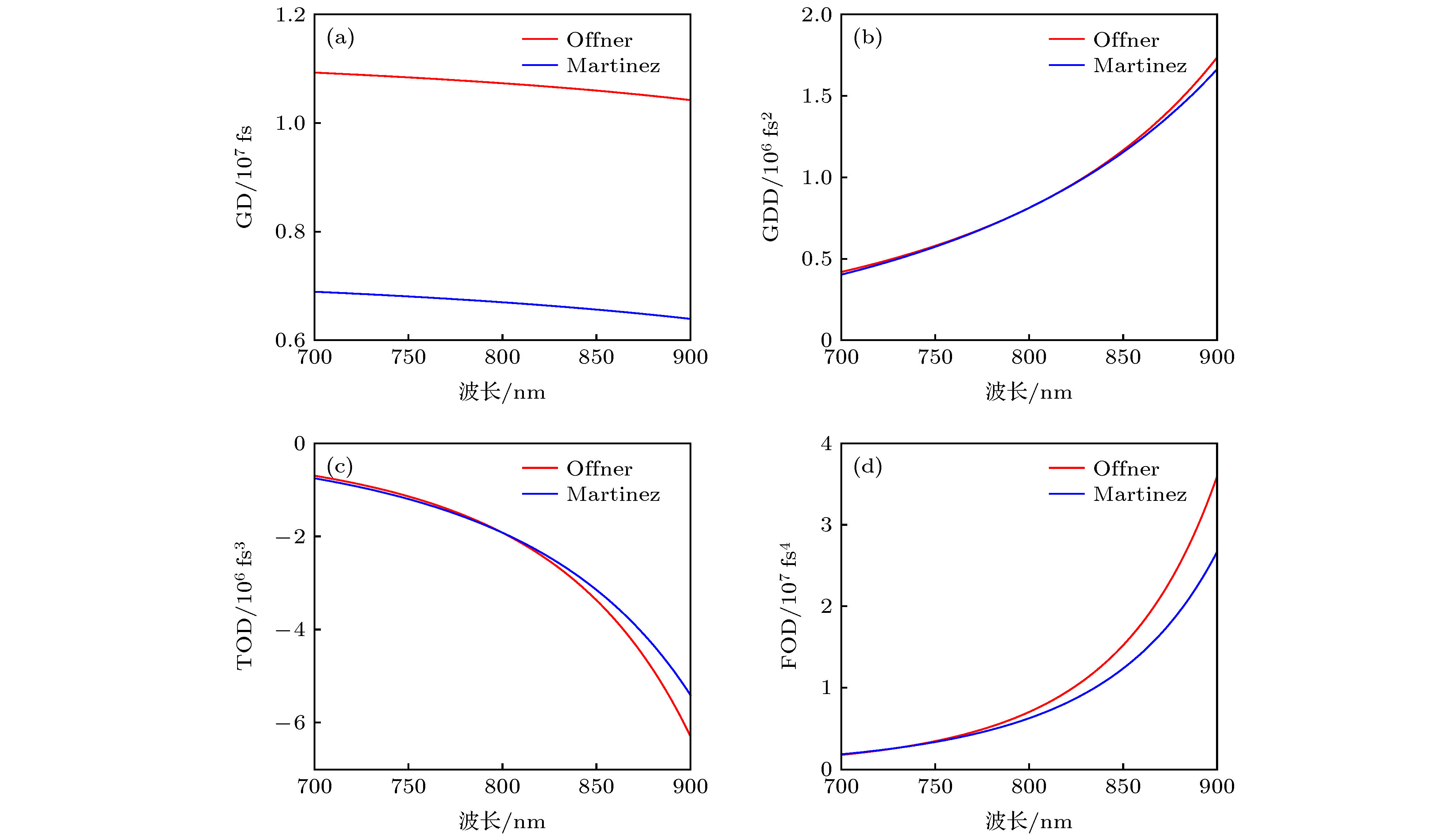
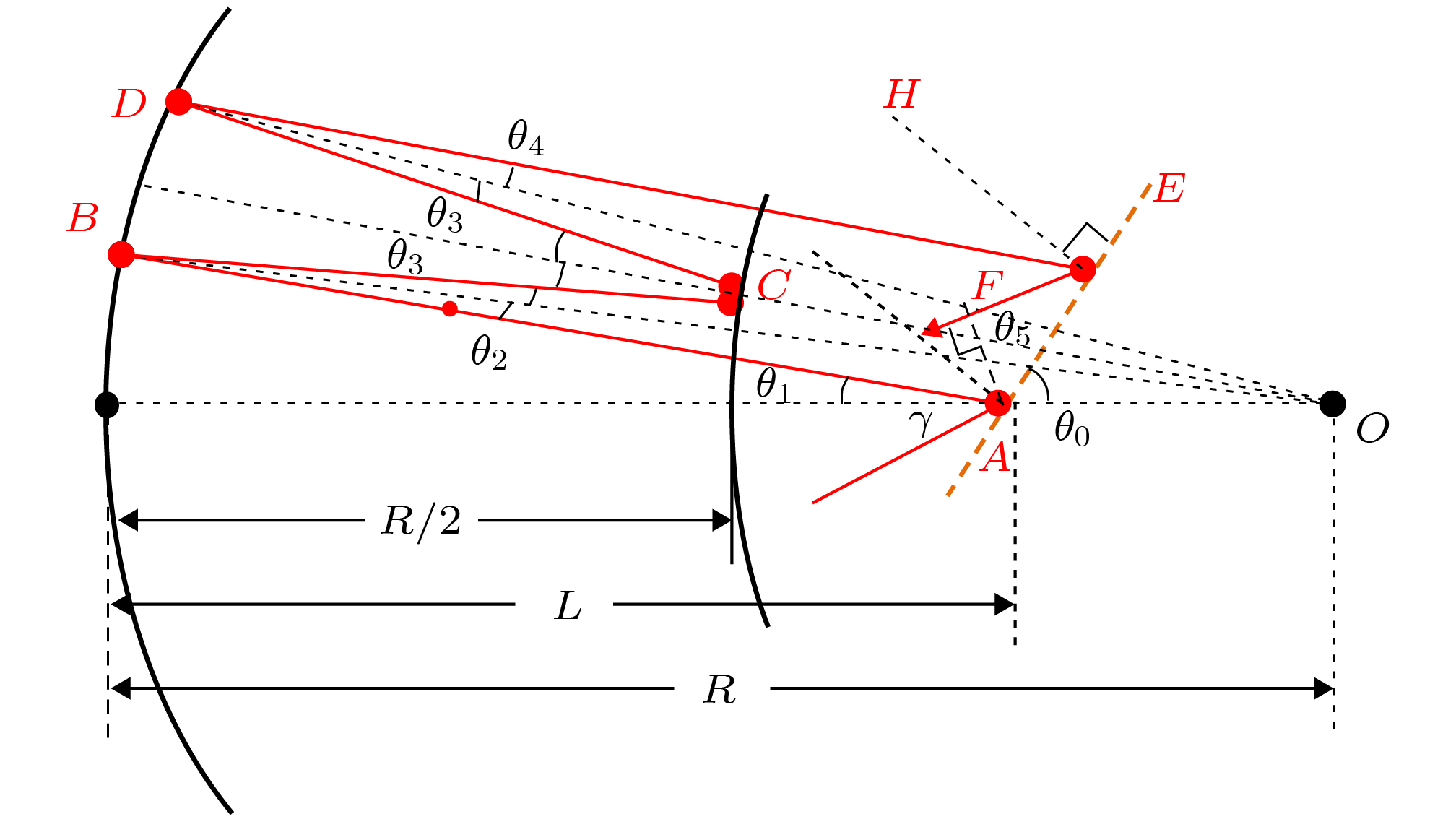
-
时域色散精密控制是超短激光产生及其应用中的关键技术之一, 它通过控制各波长的光程产生相对延迟从而改变脉冲宽度. 展宽器是啁啾脉冲放大激光系统中对激光脉冲展宽的装置, 基于光线追迹法研究光线在展宽器中的传输路径, 可计算飞秒脉冲中各波长的光程, 进而计算脉冲展宽量并应用于系统设计. 由于展宽器的光程表达式复杂, 直接对其求导获得色散表达式较困难, 目前只能采用数值导数获得近似解, 这在计算过程中会引入误差, 不利于激光系统精确设计和优化. 本文介绍了一种易实现的求解展宽器色散的解析算法, 通过归纳展宽器光程表达式特点, 引入四个基元函数, 将光程表达式分解和反复代换, 可得到高阶色散的精确解析值. 本文首先对Martinez型展宽器重新光线追迹, 获得与Offner型展宽器一致的相位表达式, 其次通过解析算法获得了两种展宽器的精确高阶色散值, 最后将解析算法与数值算法的结果进行了比较. 该解析算法对于啁啾脉冲放大系统的参数设计具有实用价值.Dispersion control is one of many key techniques in ultrashort laser pulse generation and its applications. By controlling the optical path of wavelength in the laser pulse to generate relative time delay, the pulse width of laser can be changed. The stretcher is the optical scheme to broaden the pulse width in chirp pulse amplification. By using ray trace, the pulse stretch time can be evaluated. However, due to the complicated formula of optical path in stretcher, it is difficult to obtain an analytical expression of high-order dispersion by using direct derivative. In this case, the present numerical methods are commonly used and error would be introduced into the optical system design and optimization inevitably. In this paper we introduce an analytical algorithm of stretcher dispersion. By summarizing the characteristic of stretcher formula, four fundamental functions are introduced to help to calculate the analytical derivative. By substituting the separate terms of the expressions step by step, analytical calculation of stretcher dispersion can be realized. In this paper, the ray trace of Martinez stretcher is first introduced to achieve similar phase expressions to them of existing Offner stretcher, then accurate high order dispersion results are attained by using analytical method, finally the calculation results by using the analytical method and numerical method are compared with each other. The algorithm introduced into this paper for calculating the dispersion is practical and hopeful in designing the chirp pulse amplification laser systems.
-
Keywords:
- dispersion compensation /
- chirp pulse amplification /
- pulse stretch /
- high-order dispersion
[1] Li W, Gan Z, Yu L, Wang C, Liu Y, Guo Z, Xu L, Xu M, Hang Y, Xu Y, Wang J, Huang P, Cao H, Yao B, Zhang X, Chen L, Tang Y, Li S, Liu X, Li S, He M, Yin D, Liang X, Leng Y, Li R, Xu Z 2018 Opt. Lett. 43 5681
Google Scholar
[2] Liu H, Deng X, Tong S, He C, Cheng H, Zhuang Z, Gan M, Li J, Xie W, Qiu P, Wang K 2019 Nano Lett. 19 5260
Google Scholar
[3] 秦爽, 宁笑楠, 陈九成 2019 光子学报 48 0914001
Google Scholar
Qin S, Ning X N, Chen J C 2019 Acta Phot. Sin. 48 0914001
Google Scholar
[4] Treacy E 1969 IEEE J. Quantum Electron. 5 454
Google Scholar
[5] Fork R, Martinez O, Gordon J 1984 Opt. Lett. 9 150
Google Scholar
[6] Martinez O, Gordon J, Fork R 1984 J. Opt. Soc. Am. A 1 1003
Google Scholar
[7] 张留洋, 金海洋, 曲玉秋, 浦绍质, 黄金哲, 汪东升, 杨莹 2016 激光与光电子学进展 53 102202
Zhang L Y, Jin H Y, Qu Y Q, Pu S Z, Huang J Z, Wang D S, Yang Y 2016 Laser & Optoelectronics Progress 53 102202
[8] Kane S, Squier J 1997 J. Opt. Soc. Am. B 14 661
Google Scholar
[9] Durfee C, Squier J, Kane S 2008 Opt. Express 16 18004
Google Scholar
[10] 郭淑艳, 叶蓬, 滕浩, 张伟, 李德华, 王兆华, 魏志义 2013 62 094202
Google Scholar
Guo S Y, Ye P, Teng H, Zhang W, Li D H, Wang Z H, Wei Z Y 2013 Acta Phys. Sin. 62 094202
Google Scholar
[11] 徐婷婷, 孙美智, 杨庆伟, 王楠楠, 郭爱林, 康俊, 朱海东, 谢兴龙 2013 光学学报 33 0532002
Google Scholar
Xu T T, Sun M Z, Yang Q W, Wang N N, Guo A L, Kang J, Zhu H D, Xie X L 2013 Acta Opt. Sin. 33 0532002
Google Scholar
[12] 苏娟, 刘忠华, 魏涛, 李菊芬 2015 激光与光电子进展 52 060501
Su J, Liu Z H, Wei T, Li J F 2015 Laser & Optoelectronics Progress 52 060501
[13] Bucht S, Haberberger D, Bromage J, Froula D H 2019 J. Opt. Soc. Am. B 36 2325
Google Scholar
[14] Cheriaux G, Rousseau P, Salin F, Chambaret J 1996 Opt. Lett. 21 414
Google Scholar
[15] Zhang Z, Songa Y, Suna D, Chaia L, Sunb H, Wang C 2002 Opt. Commun. 206 7
Google Scholar
[16] Jiang J, Zhang Z, Hasama T 2002 J. Opt. Soc. Am. B 19 678
[17] Wang H, Liu H, Xiong H, Zhu S, Zhao W, Wang Y, Chen G 2005 High Power Laser and Particle Beams 17 1359
[18] 田金荣, 孙敬华, 魏志义, 王兆华, 令维军, 黄小军, 刘兰亭, 魏晓峰, 张杰 2005 54 1200
Google Scholar
Tian J R, Sun J H, Wei Z Y, Wang Z H, Ling W J, Huang X J, Liu L T, Wei X F, Zhang J 2005 Acta Phys. Sin. 54 1200
Google Scholar
[19] Martinez O 1987 IEEE J. Quantum Electron. 23 59
Google Scholar
[20] Zhang Z, Yagi T, Arisawa T 1997 Appl. Opt. 36 3393
Google Scholar
[21] 王勇, 王清月, 柴路, 张伟力, 邢岐荣 2000 量子电子学报 17 193
Google Scholar
Wang Y, Wang Q Y, Chai L, Zhang W L, Xing Q R 2000 Chin. J. Quant. Elect. 17 193
Google Scholar
[22] 宋晏蓉, 张志刚, 王清月 2003 52 581
Google Scholar
Song Y R, Zhang Z G, Wang Q Y 2003 Acta Phys. Sin. 52 581
Google Scholar
[23] Su H, Peng Y J, Li Y Y, Lu X Y, Chen J C, Wang P F, Lv X L, Shao B J, Leng Y X 2019 Opt. Lett. 44 1980
Google Scholar
[24] 孙大睿, 宋晏蓉, 张志刚, 刘永军, 柴路, 王清月 2003 52 870
Google Scholar
Sun D R, Song Y R, Zhang Z G, Liu Y J, Chai L, Wang Q Y 2003 Acta Phys. Sin. 52 870
Google Scholar
[25] Backus S, Durfee C, Murnane M, Kapteyn H 1998 Rev. Sci. Instrum. 69 1207
Google Scholar
[26] 张志刚, 孙虹 2001 50 1080
Google Scholar
Zhang Z G, Sun H 2001 Acta Phys. Sin. 50 1080
Google Scholar
-
图 3 Offner型与Martinez型展宽器700−900 nm的解析计算色散曲线 (a) GD; (b) GDD; (c) TOD; (d) FOD
Fig. 3. Analytical dispersion results of Offner and Martinez stretcher: (a) GD; (b) GDD; (c) TOD; (d) FOD.
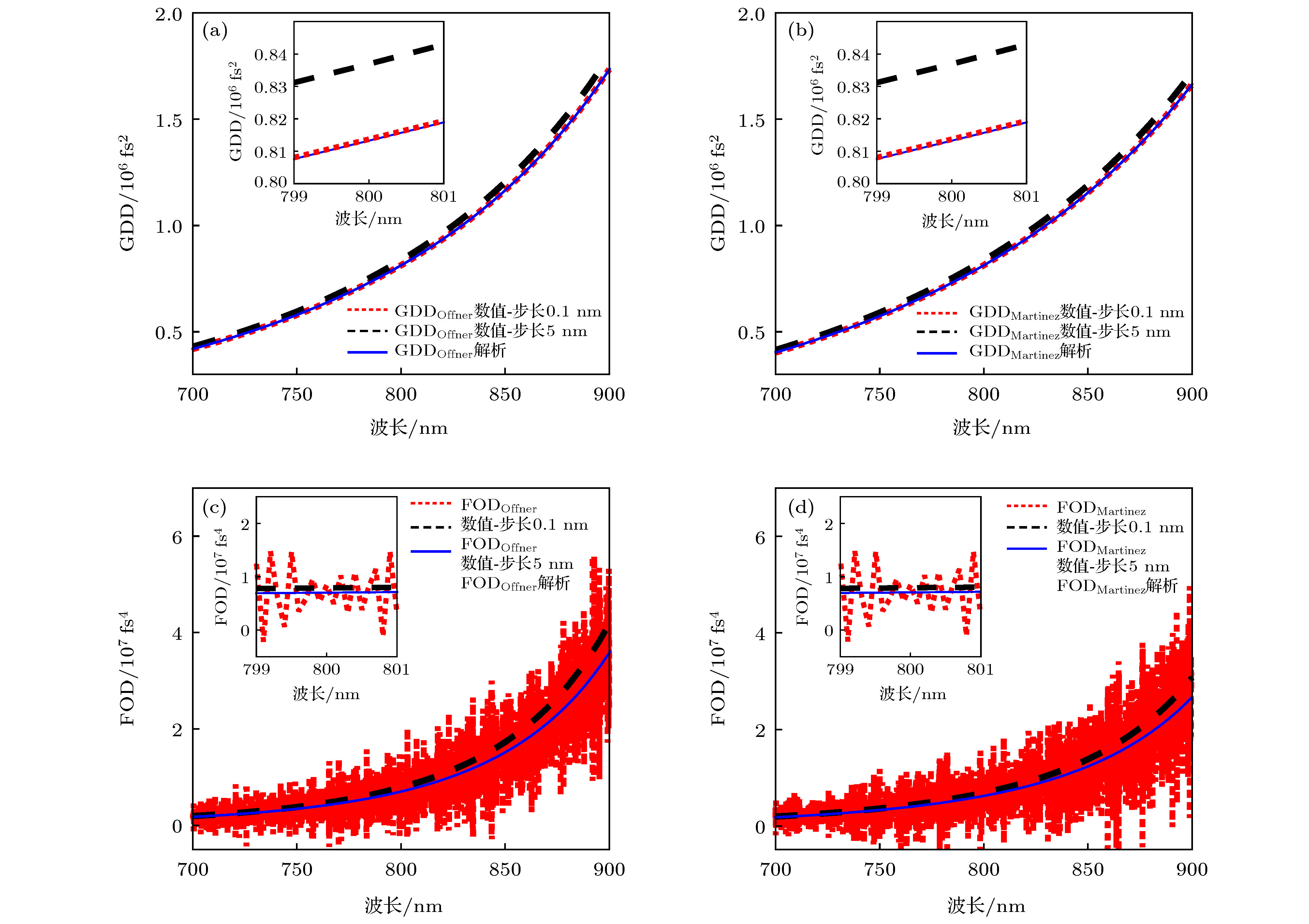
图 4 (a) Offner型展宽器的二阶色散值; (b) Martinez型展宽器的二阶色散值; (c) Offner型展宽器的四阶色散值; (d) Martinez型展宽器的四阶色散值. 图中蓝色实线为解析计算值, 红色点线是步长为0.1 nm的数值计算值, 黑色虚线是步长为5 nm的数值计算值
Fig. 4. (a) GDD of Offner stretcher; (b) GDD of Martinez stretcher; (c) FOD of Offner stretcher; (d) FOD of Martinez stretcher. Blue solid lines in the figure are analytical results; red dotted lines are numerical results with step of 0.1 nm; black dash lines are numerical results with step of 5 nm.
表 1 用于计算的Offner型与Martinez型展宽器参数
Table 1. Structural parameters of Offner and Martinez stretchers.
计算参数 Offner型
展宽器Martinez型
展宽器凹面镜曲率半径R/mm 1210 1210 光栅凹面镜间距L/mm 1005 400 激光光栅入射角γ0/(°) 22 22 光栅刻线密度/mm–1 1200 1200 展宽程数 2 2 
下载: 导出CSV
-
[1] Li W, Gan Z, Yu L, Wang C, Liu Y, Guo Z, Xu L, Xu M, Hang Y, Xu Y, Wang J, Huang P, Cao H, Yao B, Zhang X, Chen L, Tang Y, Li S, Liu X, Li S, He M, Yin D, Liang X, Leng Y, Li R, Xu Z 2018 Opt. Lett. 43 5681
Google Scholar
[2] Liu H, Deng X, Tong S, He C, Cheng H, Zhuang Z, Gan M, Li J, Xie W, Qiu P, Wang K 2019 Nano Lett. 19 5260
Google Scholar
[3] 秦爽, 宁笑楠, 陈九成 2019 光子学报 48 0914001
Google Scholar
Qin S, Ning X N, Chen J C 2019 Acta Phot. Sin. 48 0914001
Google Scholar
[4] Treacy E 1969 IEEE J. Quantum Electron. 5 454
Google Scholar
[5] Fork R, Martinez O, Gordon J 1984 Opt. Lett. 9 150
Google Scholar
[6] Martinez O, Gordon J, Fork R 1984 J. Opt. Soc. Am. A 1 1003
Google Scholar
[7] 张留洋, 金海洋, 曲玉秋, 浦绍质, 黄金哲, 汪东升, 杨莹 2016 激光与光电子学进展 53 102202
Zhang L Y, Jin H Y, Qu Y Q, Pu S Z, Huang J Z, Wang D S, Yang Y 2016 Laser & Optoelectronics Progress 53 102202
[8] Kane S, Squier J 1997 J. Opt. Soc. Am. B 14 661
Google Scholar
[9] Durfee C, Squier J, Kane S 2008 Opt. Express 16 18004
Google Scholar
[10] 郭淑艳, 叶蓬, 滕浩, 张伟, 李德华, 王兆华, 魏志义 2013 62 094202
Google Scholar
Guo S Y, Ye P, Teng H, Zhang W, Li D H, Wang Z H, Wei Z Y 2013 Acta Phys. Sin. 62 094202
Google Scholar
[11] 徐婷婷, 孙美智, 杨庆伟, 王楠楠, 郭爱林, 康俊, 朱海东, 谢兴龙 2013 光学学报 33 0532002
Google Scholar
Xu T T, Sun M Z, Yang Q W, Wang N N, Guo A L, Kang J, Zhu H D, Xie X L 2013 Acta Opt. Sin. 33 0532002
Google Scholar
[12] 苏娟, 刘忠华, 魏涛, 李菊芬 2015 激光与光电子进展 52 060501
Su J, Liu Z H, Wei T, Li J F 2015 Laser & Optoelectronics Progress 52 060501
[13] Bucht S, Haberberger D, Bromage J, Froula D H 2019 J. Opt. Soc. Am. B 36 2325
Google Scholar
[14] Cheriaux G, Rousseau P, Salin F, Chambaret J 1996 Opt. Lett. 21 414
Google Scholar
[15] Zhang Z, Songa Y, Suna D, Chaia L, Sunb H, Wang C 2002 Opt. Commun. 206 7
Google Scholar
[16] Jiang J, Zhang Z, Hasama T 2002 J. Opt. Soc. Am. B 19 678
[17] Wang H, Liu H, Xiong H, Zhu S, Zhao W, Wang Y, Chen G 2005 High Power Laser and Particle Beams 17 1359
[18] 田金荣, 孙敬华, 魏志义, 王兆华, 令维军, 黄小军, 刘兰亭, 魏晓峰, 张杰 2005 54 1200
Google Scholar
Tian J R, Sun J H, Wei Z Y, Wang Z H, Ling W J, Huang X J, Liu L T, Wei X F, Zhang J 2005 Acta Phys. Sin. 54 1200
Google Scholar
[19] Martinez O 1987 IEEE J. Quantum Electron. 23 59
Google Scholar
[20] Zhang Z, Yagi T, Arisawa T 1997 Appl. Opt. 36 3393
Google Scholar
[21] 王勇, 王清月, 柴路, 张伟力, 邢岐荣 2000 量子电子学报 17 193
Google Scholar
Wang Y, Wang Q Y, Chai L, Zhang W L, Xing Q R 2000 Chin. J. Quant. Elect. 17 193
Google Scholar
[22] 宋晏蓉, 张志刚, 王清月 2003 52 581
Google Scholar
Song Y R, Zhang Z G, Wang Q Y 2003 Acta Phys. Sin. 52 581
Google Scholar
[23] Su H, Peng Y J, Li Y Y, Lu X Y, Chen J C, Wang P F, Lv X L, Shao B J, Leng Y X 2019 Opt. Lett. 44 1980
Google Scholar
[24] 孙大睿, 宋晏蓉, 张志刚, 刘永军, 柴路, 王清月 2003 52 870
Google Scholar
Sun D R, Song Y R, Zhang Z G, Liu Y J, Chai L, Wang Q Y 2003 Acta Phys. Sin. 52 870
Google Scholar
[25] Backus S, Durfee C, Murnane M, Kapteyn H 1998 Rev. Sci. Instrum. 69 1207
Google Scholar
[26] 张志刚, 孙虹 2001 50 1080
Google Scholar
Zhang Z G, Sun H 2001 Acta Phys. Sin. 50 1080
Google Scholar
下载:
计量
- 文章访问数: 10980
- PDF下载量: 287
- 被引次数: 0
