相干与路径信息

吕鑫

doi:10.7498/aps.69.20191084

摘要

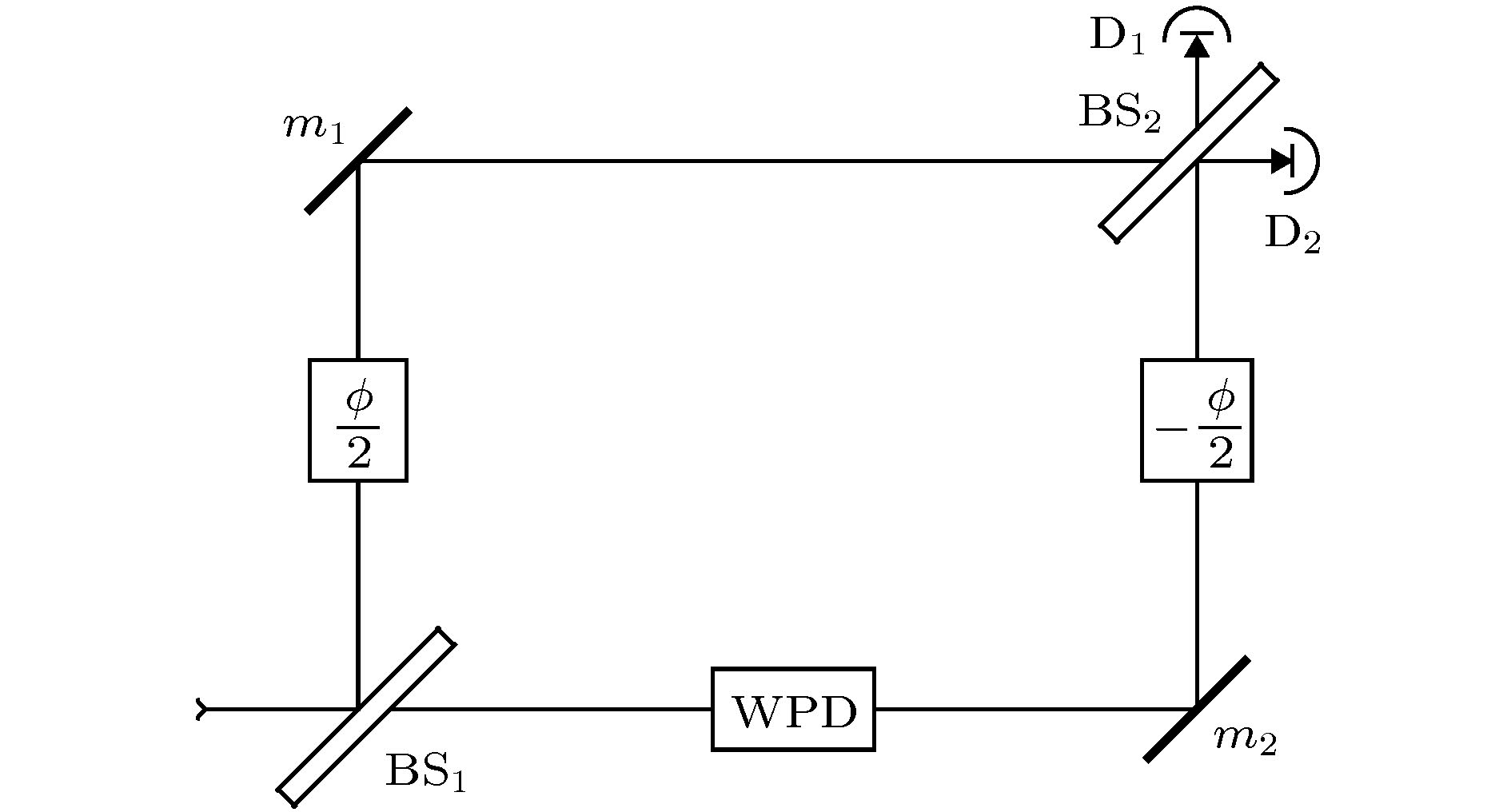
近年来, 随着对相干性量化的发展, 相干与路径信息间的互补关系渐渐引起人们注意. 这样的互补关系不仅在基础量子力学方面有重要的理论意义, 同时也在量子信息技术中有实际应用. 本文从Bures距离和明确量子态区分出发, 系统地研究了二路径干涉仪中的相干与路径信息, 并建立了一个全新的互补关系. 与已知的类似工作相比, 本文的研究更为一般: 既考虑纯态, 也考虑混合态; 既探讨了干涉仪本身的路径不对称性所提供的路径可预测性, 也探讨了因路径探测器而生的路径可区分度. 具体地说, 路径可预测性的讨论只依赖于密度矩阵的半正定性质, 而路径可区分度的讨论还需要利用保真度和Schur-Weyl不等式等工具.

关键词:

Abstract

Complementarity, or more specifically, the wave-particle duality, and quantum coherence are two fundamental concepts in quantum mechanics. Recently, motivated by the progress of the quantification of quantum coherence, the complementary relation between coherence and path information is investigated by many authors, and various duality relations between them are established. Such relations not only provide insights into fundamental problems of quantum mechanics, such as the understanding of quantum coherence and wave-particle duality; but also are important in applications of quantum technologies. In this paper, based on the Bures distance and unambiguous quantum state discrimination, systematic analysis of the complementarity between the quantum coherence and path information in two path interferometers is carried out. Similarly as other related works, the wave aspect, or the visibility of the interferometer, is quantified by the l₁-norm measure of quantum coherence, and the path information is considered via unambiguous quantum state discrimination. In this way, a novel duality relation in two path interferometers is obtained. Compared with known results, our work considers mixed states as well as pure states; considers the path predictability resulting from the intrinsic path asymmetry of the quantum state, as well as the path distinguishability resulting from the use of a which-path detector. Therefore, our work systematically generalizes known results in two path interferometers by removing all the unnecessary restrictions. Specifically, the most general form of quantum states in two path interferometers is considered and the duality relation between quantum coherence and path information is proved based on the positivity property of density matrices. The cases of path predictability and path distinguishability are considered separately. For path predictability, the proof is straightforward; whereas some advanced mathematical techniques, such as the Schur-Weyl inequality, properties of the fidelity and properties of positive matrices, are required in order to give a rigorous proof of the duality relation between coherence and path distinguishability. Concrete examples are provided to illustrate the abstract method and results. Our work concerns about two path interferometers exclusively and depends heavily that the dimensionality is two, therefore it would be an interesting task to generalize the results in this paper to n-path interferometers.

Keywords:

coherence /
complementarity /
wave-particle duality /
unambiguous quantum state discrimination

作者及机构信息

吕鑫

六盘水师范学院物理与电气工程学院, 六盘水　553000

通信作者: 吕鑫, lyuxinlps@outlook.com

基金项目: 贵州省教育厅青年科技人才成长项目(批准号: QJHKYZ[2018]377)、六盘水师范学院高层次人才科研启动基金(批准号: LPSSYKYJJ201813)、六盘水师范学院重点专业建设项目(批准号: LSZDZY2018-03)和贵州省科技厅科技平台及人才团队计划项目(批准号: QKH*Platform&Talent[2018]5777)资助的课题

Authors and contacts

Lü Xin

School of Physics and Electrical Engineering, Liupanshui Normal University, Liupanshui 553000, China

Corresponding author: Lü Xin, lyuxinlps@outlook.com

Funds: Project supported by the Young Scientific Talents Growth Project of the Department of Education of Guizhou Province (Grant No. QJHKYZ[2018]377), Research Fund for High-level Talents of Liupanshui Normal University (Grant No. LPSSYKYJJ201813), Key Disciplines Construction Project of Liupanshui Normal University (Grant No. LSZDZY2018-03) and panshui Normal University (LPSSYKYJJ201813), Science and Technology Platform and Talent team Project of Science and Technology Department of Guizhou Province (Grant No. QKH*Platform&Talent[2018]5777)

文章全文 : translate this paragraph

参考文献

[1]	Bohr N 1928 Nature 121 580 Google Scholar
[2]	Scully M O, Englert B G, Walther H 1991 Nature 351 111 Google Scholar
[3]	Wootters W K, Zurek W H 1979 Phys. Rev. D 19 473 Google Scholar
[4]	Greenberger D M, Yasin A 1988 Phys. Lett. A 128 391 Google Scholar
[5]	Jaeger G, Shimony A, Vaidman L 1995 Phys. Rev. A 51 54 Google Scholar
[6]	Englert B G 1996 Phys. Rev. Lett. 77 2154 Google Scholar
[7]	Englert B G, Bergou J A 2000 Opt. Commun. 179 337 Google Scholar
[8]	Dürr S 2001 Phys. Rev. A 64 42113 Google Scholar
[9]	Englert B G, Kaszlikowski D, Kwek L C, Chee W H 2008 Int. J. Quantum Inf. 06 129 Google Scholar
[10]	Li L, Liu N L, Yu S 2012 Phys. Rev. A 85 054101 Google Scholar
[11]	Huang J H, Wölk S, Zhu S Y, Zubairy M S 2013 Phys. Rev. A 87 022107 Google Scholar
[12]	Jia A A, Huang J H, Feng W, Zhang T C, Zhu S Y 2014 Chin. Phys. B 23 030307 Google Scholar
[13]	Angelo R M, Ribeiro A D 2015 Found. Phys. 45 1407 Google Scholar
[14]	Bera M N, Qureshi T, Siddiqui M A, Pati A k 2015 Phys. Rev. A 92 012118 Google Scholar
[15]	Bagan E, Bergou J A, Cottrell S S, Hillery M 2016 Phys. Rev. Lett. 116 160406 Google Scholar
[16]	Bagan E, Calsamiglia J, Bergou J A, Hillery M 2018 Phys. Rev. Lett. 120 050402 Google Scholar
[17]	傅双双, 骆顺龙, 孙源 2019 68 030301 Google Scholar Fu S, Luo S, Sun Y 2019 Acta Phys. Sin. 68 030301 Google Scholar
[18]	Summhammer J, Rauch H, Tuppinger D 1987 Phys. Rev. A 36 4447 Google Scholar
[19]	Dürr S, Nonn T, Rempe G 1998 Nature 395 33 Google Scholar
[20]	Dürr S, Nonn T, Rempe G 1998 Phys. Rev. Lett. 81 5705 Google Scholar
[21]	Mei M, Weitz M 2001 Phys. Rev. Lett. 86 559 Google Scholar
[22]	Trifonov A, Björk G, Söderholm, Tsegaye T 2002 Eur. Phys. J. D 18 251
[23]	Tang J S, Li Y L, Xu X Y, Xiang G Y, Li C F, Guo G C 2012 Nat. Photonics 6 600 Google Scholar
[24]	Peruzzo A, Shadbolt P, Brunner N, Popescu S, O’Brien J L 2012 Science 338 634 Google Scholar
[25]	Kaiser F, Coudreau T, Milman P, Ostrowsky D B, Tanzilli S 2012 Science 338 637 Google Scholar
[26]	Tang J S, Li Y L, Li C F, Guo G C 2013 Phys. Rev. A 88 014103 Google Scholar
[27]	Huang J H, Liu H Y, Gao J R, Zubairy M S, Zhu S Y 2013 Phys. Rev. A 88 013828 Google Scholar
[28]	Jia A A, Huang J H, Zhang T C, Zhu S Y 2014 Phys. Rev. A 89 042103 Google Scholar
[29]	Wang Z, Tian Y, Yang C, Zhang P, Li G, Zhang T 2016 Phys. Rev. A 94 062124 Google Scholar
[30]	Levi F, Mintert F 2014 New J. Phys. 16 033007 Google Scholar
[31]	Baumgratz T, Cramer M, Plenio M B 2014 Phys. Rev. Lett. 113 140401 Google Scholar
[32]	Girolami D 2014 Phys. Rev. Lett. 113 170401 Google Scholar
[33]	Streltsov A, Singh U, Dhar H S, Bera M N, Adesso G 2015 Phys. Rev. Lett. 115 020403 Google Scholar
[34]	Pires D P, Celeri L C, Soares-Pinto D O 2015 Phys. Rev. A 91 042330 Google Scholar
[35]	Yao Y, Xiao X, Ge L, Sun C P 2015 Phys. Rev. A 92 022112 Google Scholar
[36]	Winter A, Yang D 2016 Phys. Rev. Lett. 116 120404 Google Scholar
[37]	Ma J, Yadin B, Girolami D, Vedral V, Gu M 2016 Phys. Rev. Lett. 116 160407 Google Scholar
[38]	Chang L, Luo S, Sun Y 2017 Commun. Theor. Phys. 68 565 Google Scholar
[39]	Streltsov A, Adesso G, Plenio M B 2017 Rev. Mod. Phys. 89 041003 Google Scholar
[40]	Luo S, Sun Y 2017 Phys. Rev. A 96 022130 Google Scholar
[41]	Luo S, Sun Y 2017 Phys. Rev. A 96 022136 Google Scholar
[42]	Yao Y, Dong G H, Xiao X, Li M, Sun C P 2017 Phys. Rev. A 96 052322 Google Scholar
[43]	Jin Z X, Fei S M 2018 Phys. Rev. A 97 062342 Google Scholar
[44]	Bures D 1969 Trans. Amer. Math. Soc. 135 199
[45]	Bengtsson I, Życzkowski K 2006 Geometry of Quantum States: An Introduction to Quantum Entanglement (Cambridge: Cambridge University Press) p258, pp396–401
[46]	Nielsen, M A, Chuang I L 2000 Quantum Computation and Quantum Information (10th Anniversary Edition) (New York: Cambridge University Press) pp60–111, 399–416
[47]	Chefles A 2000 Contemp. Phys. 41 401 Google Scholar
[48]	Bergou J A, Herzog U, Hillery M 2004 Discrimination of Quantum States in Quantum State Estimation (Berlin/ Heidelberg: Springer) pp417–465
[49]	Bae J, Kwek L C 2015 J. Phys. A: Math. Gen. 48 083001 Google Scholar
[50]	Feng Y, Duan R, Ying M 2004 Phys. Rev. A 70 012308 Google Scholar
[51]	Uhlmann A 2000 Phys. Rev. A 62 032307 Google Scholar
[52]	Jozsa R 1994 J. Mod. Opt. 41 2315 Google Scholar
[53]	Bhatia R 2007 Positive Definite Matrices (Princeton/Oxford: Princeton University Press) pp5–12
[54]	Bellman R 1968 Linear Algebra Appl. 1 321 Google Scholar
[55]	König H 1979 Studia Math. 65 141 Google Scholar
[56]	König H 1986 Eigenvalue Distribution of Compact Operators (Basel: Birkhauser) p35
[57]	Pietsch A 1987 Eigenvalues and s-numbers (Leipzig: Geest & Portig) p155
[58]	Reed M, Simon B 1978 Methods of Modern Mathematical Physics IV: Analysis of Operators (New York: Academic) p318

施引文献

图 1 明确量子态区分在有噪信道中的体现

Fig. 1. Unambiguous quantum state discrimination in a noisy quantum channel

下载: 全尺寸图片幻灯片

图 2 利用路径探测器(WPD)的Mach-Zehnder干涉仪

Fig. 2. The Mach-Zehnder interferometer with a which-path detector

下载: 全尺寸图片幻灯片

map

[1]	Bohr N 1928 Nature 121 580 Google Scholar
[2]	Scully M O, Englert B G, Walther H 1991 Nature 351 111 Google Scholar
[3]	Wootters W K, Zurek W H 1979 Phys. Rev. D 19 473 Google Scholar
[4]	Greenberger D M, Yasin A 1988 Phys. Lett. A 128 391 Google Scholar
[5]	Jaeger G, Shimony A, Vaidman L 1995 Phys. Rev. A 51 54 Google Scholar
[6]	Englert B G 1996 Phys. Rev. Lett. 77 2154 Google Scholar
[7]	Englert B G, Bergou J A 2000 Opt. Commun. 179 337 Google Scholar
[8]	Dürr S 2001 Phys. Rev. A 64 42113 Google Scholar
[9]	Englert B G, Kaszlikowski D, Kwek L C, Chee W H 2008 Int. J. Quantum Inf. 06 129 Google Scholar
[10]	Li L, Liu N L, Yu S 2012 Phys. Rev. A 85 054101 Google Scholar
[11]	Huang J H, Wölk S, Zhu S Y, Zubairy M S 2013 Phys. Rev. A 87 022107 Google Scholar
[12]	Jia A A, Huang J H, Feng W, Zhang T C, Zhu S Y 2014 Chin. Phys. B 23 030307 Google Scholar
[13]	Angelo R M, Ribeiro A D 2015 Found. Phys. 45 1407 Google Scholar
[14]	Bera M N, Qureshi T, Siddiqui M A, Pati A k 2015 Phys. Rev. A 92 012118 Google Scholar
[15]	Bagan E, Bergou J A, Cottrell S S, Hillery M 2016 Phys. Rev. Lett. 116 160406 Google Scholar
[16]	Bagan E, Calsamiglia J, Bergou J A, Hillery M 2018 Phys. Rev. Lett. 120 050402 Google Scholar
[17]	傅双双, 骆顺龙, 孙源 2019 68 030301 Google Scholar Fu S, Luo S, Sun Y 2019 Acta Phys. Sin. 68 030301 Google Scholar
[18]	Summhammer J, Rauch H, Tuppinger D 1987 Phys. Rev. A 36 4447 Google Scholar
[19]	Dürr S, Nonn T, Rempe G 1998 Nature 395 33 Google Scholar
[20]	Dürr S, Nonn T, Rempe G 1998 Phys. Rev. Lett. 81 5705 Google Scholar
[21]	Mei M, Weitz M 2001 Phys. Rev. Lett. 86 559 Google Scholar
[22]	Trifonov A, Björk G, Söderholm, Tsegaye T 2002 Eur. Phys. J. D 18 251
[23]	Tang J S, Li Y L, Xu X Y, Xiang G Y, Li C F, Guo G C 2012 Nat. Photonics 6 600 Google Scholar
[24]	Peruzzo A, Shadbolt P, Brunner N, Popescu S, O’Brien J L 2012 Science 338 634 Google Scholar
[25]	Kaiser F, Coudreau T, Milman P, Ostrowsky D B, Tanzilli S 2012 Science 338 637 Google Scholar
[26]	Tang J S, Li Y L, Li C F, Guo G C 2013 Phys. Rev. A 88 014103 Google Scholar
[27]	Huang J H, Liu H Y, Gao J R, Zubairy M S, Zhu S Y 2013 Phys. Rev. A 88 013828 Google Scholar
[28]	Jia A A, Huang J H, Zhang T C, Zhu S Y 2014 Phys. Rev. A 89 042103 Google Scholar
[29]	Wang Z, Tian Y, Yang C, Zhang P, Li G, Zhang T 2016 Phys. Rev. A 94 062124 Google Scholar
[30]	Levi F, Mintert F 2014 New J. Phys. 16 033007 Google Scholar
[31]	Baumgratz T, Cramer M, Plenio M B 2014 Phys. Rev. Lett. 113 140401 Google Scholar
[32]	Girolami D 2014 Phys. Rev. Lett. 113 170401 Google Scholar
[33]	Streltsov A, Singh U, Dhar H S, Bera M N, Adesso G 2015 Phys. Rev. Lett. 115 020403 Google Scholar
[34]	Pires D P, Celeri L C, Soares-Pinto D O 2015 Phys. Rev. A 91 042330 Google Scholar
[35]	Yao Y, Xiao X, Ge L, Sun C P 2015 Phys. Rev. A 92 022112 Google Scholar
[36]	Winter A, Yang D 2016 Phys. Rev. Lett. 116 120404 Google Scholar
[37]	Ma J, Yadin B, Girolami D, Vedral V, Gu M 2016 Phys. Rev. Lett. 116 160407 Google Scholar
[38]	Chang L, Luo S, Sun Y 2017 Commun. Theor. Phys. 68 565 Google Scholar
[39]	Streltsov A, Adesso G, Plenio M B 2017 Rev. Mod. Phys. 89 041003 Google Scholar
[40]	Luo S, Sun Y 2017 Phys. Rev. A 96 022130 Google Scholar
[41]	Luo S, Sun Y 2017 Phys. Rev. A 96 022136 Google Scholar
[42]	Yao Y, Dong G H, Xiao X, Li M, Sun C P 2017 Phys. Rev. A 96 052322 Google Scholar
[43]	Jin Z X, Fei S M 2018 Phys. Rev. A 97 062342 Google Scholar
[44]	Bures D 1969 Trans. Amer. Math. Soc. 135 199
[45]	Bengtsson I, Życzkowski K 2006 Geometry of Quantum States: An Introduction to Quantum Entanglement (Cambridge: Cambridge University Press) p258, pp396–401
[46]	Nielsen, M A, Chuang I L 2000 Quantum Computation and Quantum Information (10th Anniversary Edition) (New York: Cambridge University Press) pp60–111, 399–416
[47]	Chefles A 2000 Contemp. Phys. 41 401 Google Scholar
[48]	Bergou J A, Herzog U, Hillery M 2004 Discrimination of Quantum States in Quantum State Estimation (Berlin/ Heidelberg: Springer) pp417–465
[49]	Bae J, Kwek L C 2015 J. Phys. A: Math. Gen. 48 083001 Google Scholar
[50]	Feng Y, Duan R, Ying M 2004 Phys. Rev. A 70 012308 Google Scholar
[51]	Uhlmann A 2000 Phys. Rev. A 62 032307 Google Scholar
[52]	Jozsa R 1994 J. Mod. Opt. 41 2315 Google Scholar
[53]	Bhatia R 2007 Positive Definite Matrices (Princeton/Oxford: Princeton University Press) pp5–12
[54]	Bellman R 1968 Linear Algebra Appl. 1 321 Google Scholar
[55]	König H 1979 Studia Math. 65 141 Google Scholar
[56]	König H 1986 Eigenvalue Distribution of Compact Operators (Basel: Birkhauser) p35
[57]	Pietsch A 1987 Eigenvalues and s-numbers (Leipzig: Geest & Portig) p155
[58]	Reed M, Simon B 1978 Methods of Modern Mathematical Physics IV: Analysis of Operators (New York: Academic) p318

[1]	李保民, 胡明亮, 范桁. 量子相干. , 2019, 68(3): 030304. doi: 10.7498/aps.68.20181779
[2]	田聪, 鹿翔, 张英杰, 夏云杰. 纠缠相干光场对量子态最大演化速率的操控. , 2019, 68(15): 150301. doi: 10.7498/aps.68.20190385
[3]	傅双双, 骆顺龙, 孙源. 相干与信息守恒及其在Mach-Zehnder干涉中的应用. , 2019, 68(3): 030301. doi: 10.7498/aps.68.20181778
[4]	蔡伟, 邢俊晖, 杨志勇. 磁光材料Verdet常数贡献性的讨论. , 2017, 66(18): 187801. doi: 10.7498/aps.66.187801
[5]	贺志, 李莉, 姚春梅, 李艳. 利用量子相干性判定开放二能级系统中非马尔可夫性. , 2015, 64(14): 140302. doi: 10.7498/aps.64.140302
[6]	李成强, 王挺峰, 张合勇, 谢京江, 刘立生, 郭劲. 光源参数及大气湍流对电磁光束传输偏振特性的影响. , 2014, 63(10): 104201. doi: 10.7498/aps.63.104201
[7]	张颖, 刘兰琴, 王文义, 黄晚晴, 耿远超, 谢旭东, 朱启华. 激光脉冲前后沿相干叠加对多程放大的影响. , 2014, 63(18): 184205. doi: 10.7498/aps.63.184205
[8]	孙新梅, 查新未, 祁建霞, 兰倩. 基于非最大纠缠的五粒子Cluster态的高效量子态共享方案. , 2013, 62(23): 230302. doi: 10.7498/aps.62.230302
[9]	余海军, 杜建明, 张秀兰. 相干态的小波变换. , 2012, 61(16): 164205. doi: 10.7498/aps.61.164205
[10]	程治明, 吴逢铁, 方翔, 范丹丹, 朱健强. 圆顶轴棱锥产生多个局域空心光束. , 2012, 61(21): 214201. doi: 10.7498/aps.61.214201
[11]	邓勇, Meglinski Igor. Monte Carlo方法模拟光在生物组织中传播的新进展. , 2010, 59(2): 1396-1401. doi: 10.7498/aps.59.1396
[12]	马海强, 李林霞, 王素梅, 吴张斌, 焦荣珍. 一种全光纤型观测光波粒二象性的方法. , 2010, 59(1): 75-79. doi: 10.7498/aps.59.75
[13]	刘春旭, 张继森, 刘俊业, 金光. Er3+：YAlO3晶体中Λ型四能级系统的量子相干左手性. , 2009, 58(8): 5778-5783. doi: 10.7498/aps.58.5778
[14]	李文博, 李宓善, 李亚玲, 温晓阳, 袁广军, 张驰, 杨涛. 三粒子Calogero-Sutherland模型的相干态. , 2008, 57(5): 2674-2679. doi: 10.7498/aps.57.2674
[15]	叶宾, 须文波, 顾斌杰. 量子Harper模型的量子计算鲁棒性与耗散退相干. , 2008, 57(2): 689-695. doi: 10.7498/aps.57.689
[16]	马瑞琼, 李永放, 时坚. 量子态的非相干光时域测量. , 2008, 57(9): 5593-5599. doi: 10.7498/aps.57.5593
[17]	刘婷婷, 王大威, 陆伟新, 孙泉, 杨宏, 蒋红兵, 龚旗煌. 双光束相干控制产生多次谐波的实验验证. , 2003, 52(4): 864-869. doi: 10.7498/aps.52.864
[18]	郭红霞, 陈雨生, 张义门, 周辉, 龚建成, 韩福斌, 关颖, 吴国荣. 稳态、瞬态X射线辐照引起的互补性金属-氧化物-半导体器件剂量增强效应研究. , 2001, 50(12): 2279-2283. doi: 10.7498/aps.50.2279
[19]	邢永忠, 徐躬耦. 经典混沌系统在相应于初始相干态的量子子空间中的随机性. , 1999, 48(5): 769-774. doi: 10.7498/aps.48.769
[20]	黄洪斌. 超导体中库珀对的SU(2)与Glauber相干态——库珀对与约瑟夫森超流性的量子特性研究. , 1991, 40(9): 1402-1410. doi: 10.7498/aps.40.1402

计量

文章访问数: 7268
PDF下载量: 89
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

相干与路径信息