拓扑绝缘体中的超快电荷自旋动力学

向天; 程亮; 齐静波

doi:10.7498/aps.68.20191433

摘要

拓扑绝缘体是根据动量空间的拓扑不变量来定义的一类区别于普通绝缘体的新兴拓扑非平庸材料, 其体态和表面态分别表现为绝缘和金属性质, 并且其表面态具有独特的自旋结构(自旋-动量锁定), 因此该类材料在光电器件和自旋电子器件领域有很多潜在的应用. 由于开展这些应用研究首先需要对这类材料中的电荷与自旋动力学有全面的了解, 所以拓扑绝缘体中的非平衡物理性质的研究引起了人们极大兴趣. 本文对这一研究领域所作的研究工作做了一个较全面的描述, 特别是跟时间分辨超快光谱相关的实验工作. 并希望文中的讨论能激发研究者尤其是理论工作者对这一领域进一步的探讨, 同时期待目标研究对象也能扩展到其他拓扑材料体系.

关键词:

Abstract

Topological insulators (TIs), with unique bulk insulating and two-dimensional surface conducting states, show great promise of future optospintronics and spintronics applications, where a complete knowledge of the charge and spin dynamics is quite essential. Thus, the non-equilibrium properties inside TIs have attracted enormous attention. Here in this paper, we review the latest achievements in this field. The focus will be mainly on the experimental study, covering the ultrafast dynamical properties of charge, phonon, and spin. We hope that this review can stimulate further studies, especially theoretical research concerning the properties of topological insulators out of thermodynamic equilibrium.

Keywords:

作者及机构信息

1.
电子科技大学, 电子薄膜与集成器件国家重点实验室, 成都　611731

2.
电子科技大学广东电子信息工程研究院, 东莞　523808

通信作者: 齐静波, jbqi@uestc.edu.cn

基金项目: 国家自然科学基金(批准号: 11974070, 11734006)和广东东莞市核心技术攻关前沿项目(批准号: 2019622101004)资助的课题

Authors and contacts

1.
State Key Laboratory of Electronic Thin Films and Integrated Devices, University of Electronic Science and Technology of China, Chengdu 611731, China

2.
Guangdong Institute of Electronic Information Engineering, University of Electronic Science and Technology, Dongguan 523808, China

Corresponding author: Qi Jing-Bo, jbqi@uestc.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11974070, 11734006) and the Frontier Science Project of Dongguan, China (No. 2019622101004)

文章全文 : translate this paragraph

参考文献

[1]	Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057 Google Scholar
[2]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
[3]	Zhang H J, Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2009 Nat. Phys. 5 438 Google Scholar
[4]	Hajlaoui M, Papalazarou E, Mauchain J, Lantz G, Moisan N, Boschetto D, Jiang Z, Miotkowski I, Chen Y P, Taleb-Ibrahimi A, Perfetti L, Marsi M 2012 Nano Lett. 12 3532 Google Scholar
[5]	Xia Y, Wray L, Qian D, Hsieh D, Pal A, Lin H, Bansil A, Grauer D, Hor Y S, Cava R J, Hasan M Z 2008 arXiv 0812 2078
[6]	Hsieh D, Xia Y, Qian D, Wray L, Dil J H, Osterwalder J, Patthey L, Checkelsky J G, Ong N P, Fedorov A V, Lin H, Bansil A, Grauer D, Hor Y S, Cava R J, Hasan M Z 2009 Nature 460 1101 Google Scholar
[7]	Qi J, Chen X, Yu W, Cadden-Zimansky P, Smirnov D, Tolk N H, Miotkowski I, Cao H, Chen Y P, Wu Y, Qiao S, Jiang Z 2010 Appl. Phys. Lett. 97 182102 Google Scholar
[8]	Wang M C, Qiao S, Jiang Z, Luo S N, Qi J 2016 Phys. Rev. Lett. 116 036601 Google Scholar
[9]	王明聪 2017 强关联及拓扑材料的超快光谱研究 (绵阳: 中国工程物理研究院) Wang M C 2017 Ultrafast optical spectroscopy research of strong correlated and topological materials (Mianyang: China Academy of Engineering Physics)(in Chinese)
[10]	Basov D N, Averitt R D, Van Der Marel D, Dressel M, Haule, K 2011 Rev. Mod. Phys. 83 471 Google Scholar
[11]	Kumar N, Brian A R, Butch N P, Syers P, Kirshenbaum K, Paglione J, Zhao H 2011 Phys. Rev. B 83 235306 Google Scholar
[12]	Luo L, Yang X, Liu X, Liu Z, Vaswani C, Cheng D, Mootz M, Zhao X, Yao Y, Wang C Z, Ho K M, Perakis I E, Dobrowolska M, Furdyna J K, Wang J 2019 Nat. Commun. 10 607 Google Scholar
[13]	Sobota J A, Yang S, Analytis J G, Chen Y L, Fisher I R, Kirchmann P S, and Shen Z X 2012 Phys. Rev. Lett. 108 117403 Google Scholar
[14]	Hsieh D, Mahmood F, McIver J W, Gardner D R, Lee Y S, Gedik N 2011 Phys. Rev. Lett. 107 077401 Google Scholar
[15]	Zouaghi W, Thomson M D, Rabia K, Hahn R, Blank V, Roskos H G 2013 Eur. J. Phys. 34 S179 Google Scholar
[16]	Smith P R, Auston D H, Nuss M C 1988 IEEE J. Quantum Electron. 24 255 Google Scholar
[17]	Averitt R D, Taylor A J 2002 J. Phys.: Condens. Matter 14 R1357
[18]	Eschenlohr A, Battiato M, Maldonado P, Pontius N, Kachel T, Holldack K, Mitzner R, Föhlisch A, Oppeneer P M, Stamm C 2013 Nat. Mater. 12 332 Google Scholar
[19]	Demsar J, Sarrao J L, Taylor A J 2006 J. Phys.: Condens. Matter 18 R281 Google Scholar
[20]	Kastler A 1957 JOSA 47 460 Google Scholar
[21]	Fabian J, Sarma S Das 2004 Rev. Mod. Phys. 76 323 Google Scholar
[22]	Richard P, Sato T, Nakayama K, Takahashi T, Ding H 2011 Reports Prog. Phys. 74 124512 Google Scholar
[23]	Eich S, Stange A, Carr A V, Urbancic J, Popmintchev T, Wiesenmayer M, Jansen K, Ruffing A, Jakobs S, Rohwer T, Hellmann S, Chen C, Matyba P, Kipp L, Rossnagel K, Bauer M, Murnane M M, Kapteyn H C, Mathias S, Aeschlimann M 2014 J. Electron Spectros. Relat. Phenomena 195 231 Google Scholar
[24]	Cacho C, Crepaldi A, Battiato M, Braun J, Cilento F, Zacchigna M, Richter M C, Heckmann O, Springate E, Liu Y, Dhesi S S, Berger H, Bugnon Ph, Held K, Grioni M, Ebert H, Hricovini K, Minár J, Parmigiani F 2015 Phys. Rev. Lett. 114 097401 Google Scholar
[25]	Glinka Y D, Babakiray S, Johnson T A, Holcomb M B, Lederman D 2014 Appl. Phys. Lett. 105 171905 Google Scholar
[26]	Lai Y P, Chen H J, Wu K H, Liu J M 2014 Appl. Phys. Lett. 105 232110 Google Scholar
[27]	Weis M, Balin K, Rapacz R, Nowak A, Lejman M, Szade J, Ruello P 2015 Phys. Rev. B 92 014301 Google Scholar
[28]	Sánchez-Barriga J, Battiato M, Krivenkov M, Golias E, Varykhalov A, Romualdi A, Yashina L V, Minár J, Kornilov O, Ebert H, Held K, Braun J 2017 Phys. Rev. B 95 125405 Google Scholar
[29]	李正中 2002 固体理论 (第2版) (北京:高等教育出版社) 第 40 页 Li Z Z 2002 Solid Theory (2nd Ed.) (Beijing: Higher Education Press) p40 (in Chinese)
[30]	Cheng L, La-O-Vorakiat C, Tang C S, Nair S K, Xia B, Wang L, Zhu J X, Chia Elbert E M 2014 Appl. Phys. Lett. 104 211906 Google Scholar
[31]	Pan Z H, Fedorov A V, Gardner D, Lee Y S, Chu S, Valla T 2012 Phys. Rev. Lett. 108 187001 Google Scholar
[32]	Valdés Aguilar R, Qi J, Brahlek M, Bansal N, Azad A, Bowlan J, Oh S, Taylor A J, Prasankumar R P, Yarotski D A 2015 Appl. Phys. Lett. 106 011901 Google Scholar
[33]	Wu L, Brahlek M, Aguilar R Valdés, Stier A V, Morris C M, Lubashevsky Y, Bilbro L S, Bansal N, Oh S, Armitage N P 2013 Nat. Phys. 9 410 Google Scholar
[34]	Valdés Aguilar R, Stier A V, Liu W, Bilbro L S, George D K, Bansal N, Wu L, Cerne J, Markelz A G, Oh S, Armitage N P 2012 Phys. Rev. Lett. 108 087403 Google Scholar
[35]	Choi Y G, Zhung C J, Park S H, Park J B, Kim J S, Kim S H, Park J H, Lee J S 2018 Phys. Rev. B 97 075307 Google Scholar
[36]	Wang Y H, Hsieh D, Sie E J, Steinberg H, Gardner D R, Lee Y S, Jarillo-Herrero P, Gedik N 2012 Phys. Rev. Lett. 109 127401 Google Scholar
[37]	Sobota J A, Yang S L, Leuenberger D, Kemper A F, Analytis J G, Fisher I R, Kirchmann P S, Devereaux T P, Shen Z X 2014 J. Electron Spectros. Relat. Phenomena 195 249 Google Scholar
[38]	Saha K, Garate I 2014 Phys. Rev. B 90 245418 Google Scholar
[39]	Shapourian H, Hughes T L, Ryu S 2015 Phys. Rev. B 92 165131 Google Scholar
[40]	Yazyev O V, Moore J E, Louie S G 2010 Phys. Rev. Lett. 105 266806 Google Scholar
[41]	Liu C X, Qi X L, Zhang H J, Dai X, Fang Z, Zhang S C 2010 Phys. Rev. B 82 045122 Google Scholar
[42]	Kamaraju N, Sunil K, Sood A K 2010 Europhys. Lett. 92 47007 Google Scholar
[43]	Li Y W, Stoica Vladimir A, Endicott L, Wang G Y, Uher C, Clarke R 2010 Appl. Phys. Lett. 97 171908 Google Scholar
[44]	Wang Y, Xu X, Venkatasubramanian R 2008 Appl. Phys. Lett. 93 113114 Google Scholar
[45]	Cheng T K, Vidal J, Zeiger H. J, Dresselhaus G, Dresselhaus M S, Ippen E P 1991 Appl. Phys. Lett 59 1923 Google Scholar
[46]	Richter W, Kohler H, Becker C R 1977 Phys. Status Solidi 84 619 Google Scholar
[47]	Merlin R 1997 Solid State Commun. 102 207 Google Scholar
[48]	Sobota J A, Yang S L, Leuenberger D, Kemper A F, Analytis J G, Fisher I R, Kirchmann P S, Devereaux T P, Shen Z X 2014 Phys. Rev. Lett. 113 157401 Google Scholar
[49]	Xu Y, Khafizov M, Satrapinsky L, Kúš P, Plecenik A, Sobolewski R 2003 Phys. Rev. Lett. 91 197004 Google Scholar
[50]	Taneda T, Pepe G P, Parlato L, Golubov A A, Sobolewski R 2007 Phys. Rev. B 75 174507 Google Scholar
[51]	Giraud S, Egger R 2011 Phys. Rev. B 83 245322 Google Scholar
[52]	Giraud S, Kundu A, Egger R 2012 Phys. Rev. B 85 035441 Google Scholar
[53]	Iyer V, Chen Y P, Xu X 2018 Phys. Rev. Lett. 121 026807 Google Scholar
[54]	Hertel R 2005 arXiv:cond-mat 0509 0509060
[55]	Sobota J A, Yang S L, Kemper A F, Lee J J, Schmitt F T, Li W, Moore R G, Analytis J G, Fisher I R, Kirchmann P S, Devereaux T P, Shen Z X 2013 Phys. Rev. Lett. 111 136802 Google Scholar

施引文献

图 1 (a)反射式光学抽运-光学探测光路; (b)GaAs的典型的光学抽运-光学探测信号

Fig. 1. (a) Experimental setup of optical pump-probe spectroscopy in reflection configuration; (b) typical optical pump-probe signal of GaAs.

下载: 全尺寸图片幻灯片

图 2 (a) 电光采样法^[15]; (b) OPTP光谱光路示意图

Fig. 2. (a) Electro-optic sampling^[15]; (b) experimental setup of OPTP spectroscopy.

下载: 全尺寸图片幻灯片

图 3 (a)磁光克尔效应的原理^[9]; (b)基于抽运-探测技术的时间分辨克尔旋转光谱示意图^[8]

Fig. 3. (a) Schematic of magneto-optic Kerr effect^[9]; (b) TRKR^[8] via pump-probe technique.

下载: 全尺寸图片幻灯片

图 4 (a) ARPES 和(b) Tr-ARPES^[23]实验平台示意图

Fig. 4. Schematic of (a) ARPES and (b) Tr-ARPES^[23] setups.

下载: 全尺寸图片幻灯片

图 5 (a), (b)室温下Bi₂Se₃单晶的OPOP信号^[7,11], 其中图(b)中红色方框为探测光在Bi₂Se₃样品表面上的光斑的半高全宽随时间延时的变化^[11]

Fig. 5. (a), (b) Transient reflectivity of Bi₂Se₃ measured via OPOP at room temperature^[7,11]. The red squares in (b) show the full width half maximum of the probe light’s spot as a function of delay time^[11].

下载: 全尺寸图片幻灯片

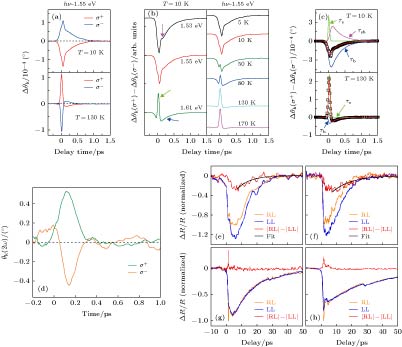
图 6 Bi₂Se₃薄膜的OPTP信号^[32]　(a)无光抽运下的Bi₂Se₃电导; (b)有光抽运下透过Bi₂Se₃的太赫兹波形; (c), (d)不同样品厚度以及不同功率下太赫兹电场峰值随着抽运延时变化; (e)—(h)为在不同抽运延迟下, 通过用Drude-Lorentz拟合的对于不同厚度样品散射率和等离子频率

Fig. 6. OPTP signals of Bi₂Se₃ thin film^[32]: (a) Conductance of Bi₂Se₃ without optical pump; (b) transmitted terahertz electric field after sample under optical pump; (c), (d) transient THz peak signal of samples with different thickness and pump power; (e)—(h) scattering rate and plasma frequency obtained from the fitting of conductance of Bi₂Se₃ by Drude-Lorentz model with different sample thickness and pump delay.

下载: 全尺寸图片幻灯片

图 7 (a), (b) Bi_1.5Sb_0.5Te_1.7Se_1.3(BSTS)和Bi₂Se₃的OPTP信号; (c), (d)BSTS和Bi₂Se₃的能带结构示意图和电子转移^[35]

Fig. 7. (a), (b) OPTP signals of Bi_1.5Sb_0.5Te_1.7Se_1.3 (BSTS) and Bi₂Se₃; (c), (d) schematic diagrams of energy bands and electron transfer in BSTS and Bi₂Se₃^[35]

下载: 全尺寸图片幻灯片

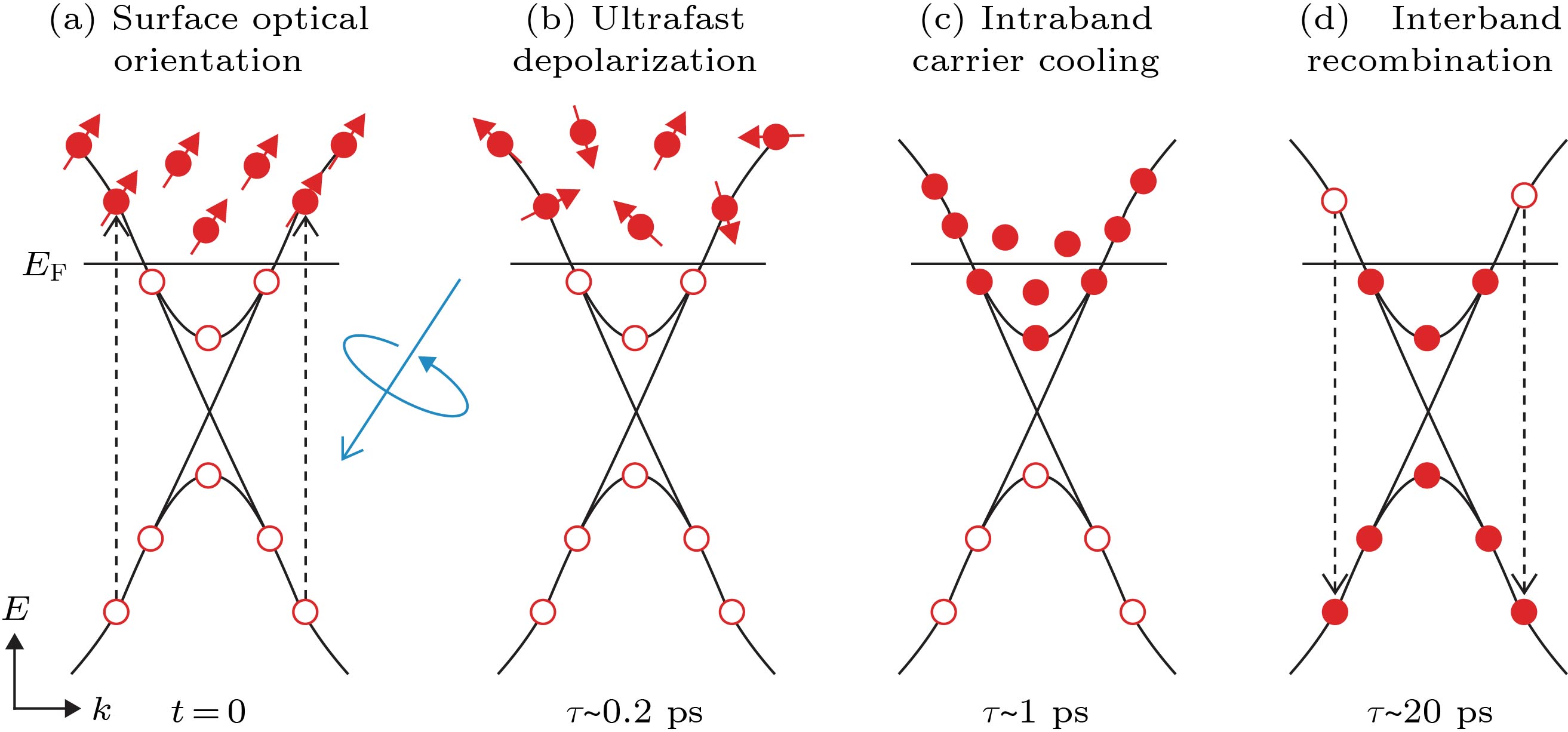
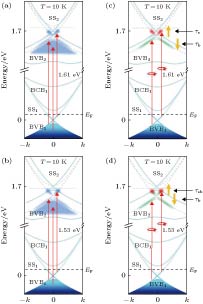
图 8 Bi₂Se₃的Tr-ARPES信号^[13]　(a) p型掺杂的Bi₂Se₃受光激发后不同能带的弛豫过程; (b)用于参考的Bi₂Se₃的能带; (c)平衡态Bi₂Se₃的能带结构, 由于掺杂导致费米能级较低, 表面态和体态导带并没有被占据; (d)在刚刚被抽运光激发时, 电子被激发到较高能级处; (e)—(g)则描述了较高能量的电子的弛豫过程

Fig. 8. Experimental Tr-ARPES data^[13]: (a) The relaxation process for different bands of p-doped Bi₂Se₃ excited by light; (b) schematic of the electronic band structures of Bi₂Se₃ for reference; (c) electronic band structures for Bi₂Se₃, and the surface states and bulk conduction band are unoccupied due to the Fermi energy sitting inside the bulk valence band; (d) electrons are excited to high energy band after the excitation; (e)–(g) relaxation process of high energy electrons.

下载: 全尺寸图片幻灯片

图 9 由Shen研究组(a)^[13]和Gedik研究组(b)^[36]利用Tr-ARPES所测得的Bi₂Se₃电子温度数据

Fig. 9. Electron temperature of Bi₂Se₃ obtained by Tr-ARPES from Shen's group (a)^[13] and Gedik's group (b)^[36].

下载: 全尺寸图片幻灯片

图 10 Bi₂Se₃的OPOP实验数据及其傅里叶变换结果^[8]

Fig. 10. OPOP experimental data and Fourier transform of the oscillatory data for Bi₂Se₃ at 293 K^[8].

下载: 全尺寸图片幻灯片

图 11 Bi₂Se₃的Tr-ARPES实验数据图^[48]

Fig. 11. Experimental Tr-ARPES data of Bi₂Se₃^[48].

下载: 全尺寸图片幻灯片

图 12 Bi₂Se₃中载流子和自旋在光激发下的弛豫过程图示^[14]　(a)−(d)不同时间尺度下的弛豫过程

Fig. 12. Photoinduced relaxation processes of carriers and spin in Bi₂Se₃ ^[14]: (a)−(d) correspond to the relaxation processes of different time scales

下载: 全尺寸图片幻灯片

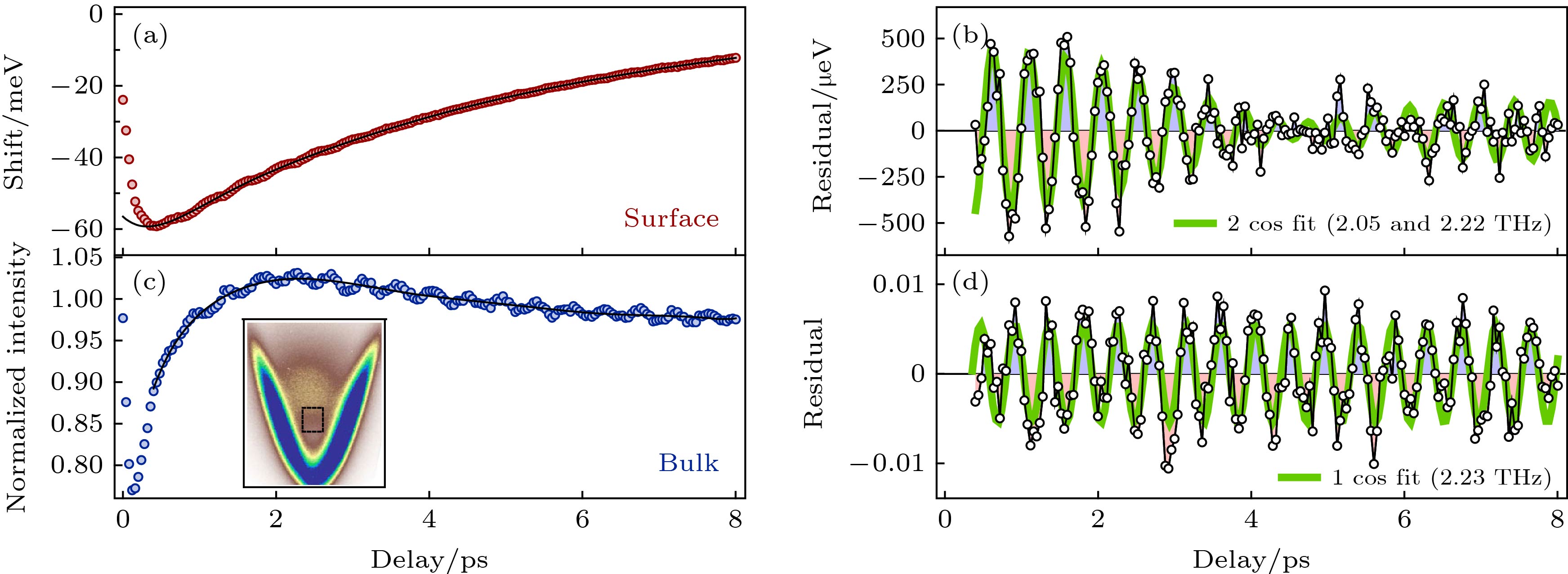
图 13 (a) Bi₂Se₃样品在10 K和80 K时的克尔转角光谱, 红线代表抽运激光为左旋圆偏振光, 蓝色实线代表右旋圆偏振光^[8]; (b) Bi₂Se₃样品在不同光子能量和不同温度下的克尔转角光谱^[8]; (c) Bi₂Se₃实验数据拟合^[8]; (d)二次谐波克尔光谱(斜入射抽运光)测得的实验数据^[14]; (e)−(h)左右圆偏振光激发后反射率变化随时间变化的实验数据^[53]

Fig. 13. (a) Time-resolved Kerr rotation of Bi₂Se₃ at 10 K and 80 K. Red line indicates that the pump laser is left circularly polarized while the blue one is right circularly polarized^[8]. (b) Time-resolved Kerr rotation of Bi₂Se₃ excited at different photon energies for different temperatures^[8]. (c) fittings of the TRKR experimental data for Bi₂Se₃^[8]. (d) Kerr rotation experimental data via second harmonic generation(oblique pump)^[14]. (e)−(h) transient reflectivity corresponding to the left and right circularly polarized pump light^[53].

下载: 全尺寸图片幻灯片

图 14 Bi₂Se₃在不同光子能量激发下的能带跃迁示意图^[8]

Fig. 14. Schematic of photo-excitation processes via light with different photon energies in Bi₂Se₃ ^[8].

下载: 全尺寸图片幻灯片

map

[1]	Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057 Google Scholar
[2]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
[3]	Zhang H J, Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2009 Nat. Phys. 5 438 Google Scholar
[4]	Hajlaoui M, Papalazarou E, Mauchain J, Lantz G, Moisan N, Boschetto D, Jiang Z, Miotkowski I, Chen Y P, Taleb-Ibrahimi A, Perfetti L, Marsi M 2012 Nano Lett. 12 3532 Google Scholar
[5]	Xia Y, Wray L, Qian D, Hsieh D, Pal A, Lin H, Bansil A, Grauer D, Hor Y S, Cava R J, Hasan M Z 2008 arXiv 0812 2078
[6]	Hsieh D, Xia Y, Qian D, Wray L, Dil J H, Osterwalder J, Patthey L, Checkelsky J G, Ong N P, Fedorov A V, Lin H, Bansil A, Grauer D, Hor Y S, Cava R J, Hasan M Z 2009 Nature 460 1101 Google Scholar
[7]	Qi J, Chen X, Yu W, Cadden-Zimansky P, Smirnov D, Tolk N H, Miotkowski I, Cao H, Chen Y P, Wu Y, Qiao S, Jiang Z 2010 Appl. Phys. Lett. 97 182102 Google Scholar
[8]	Wang M C, Qiao S, Jiang Z, Luo S N, Qi J 2016 Phys. Rev. Lett. 116 036601 Google Scholar
[9]	王明聪 2017 强关联及拓扑材料的超快光谱研究 (绵阳: 中国工程物理研究院) Wang M C 2017 Ultrafast optical spectroscopy research of strong correlated and topological materials (Mianyang: China Academy of Engineering Physics)(in Chinese)
[10]	Basov D N, Averitt R D, Van Der Marel D, Dressel M, Haule, K 2011 Rev. Mod. Phys. 83 471 Google Scholar
[11]	Kumar N, Brian A R, Butch N P, Syers P, Kirshenbaum K, Paglione J, Zhao H 2011 Phys. Rev. B 83 235306 Google Scholar
[12]	Luo L, Yang X, Liu X, Liu Z, Vaswani C, Cheng D, Mootz M, Zhao X, Yao Y, Wang C Z, Ho K M, Perakis I E, Dobrowolska M, Furdyna J K, Wang J 2019 Nat. Commun. 10 607 Google Scholar
[13]	Sobota J A, Yang S, Analytis J G, Chen Y L, Fisher I R, Kirchmann P S, and Shen Z X 2012 Phys. Rev. Lett. 108 117403 Google Scholar
[14]	Hsieh D, Mahmood F, McIver J W, Gardner D R, Lee Y S, Gedik N 2011 Phys. Rev. Lett. 107 077401 Google Scholar
[15]	Zouaghi W, Thomson M D, Rabia K, Hahn R, Blank V, Roskos H G 2013 Eur. J. Phys. 34 S179 Google Scholar
[16]	Smith P R, Auston D H, Nuss M C 1988 IEEE J. Quantum Electron. 24 255 Google Scholar
[17]	Averitt R D, Taylor A J 2002 J. Phys.: Condens. Matter 14 R1357
[18]	Eschenlohr A, Battiato M, Maldonado P, Pontius N, Kachel T, Holldack K, Mitzner R, Föhlisch A, Oppeneer P M, Stamm C 2013 Nat. Mater. 12 332 Google Scholar
[19]	Demsar J, Sarrao J L, Taylor A J 2006 J. Phys.: Condens. Matter 18 R281 Google Scholar
[20]	Kastler A 1957 JOSA 47 460 Google Scholar
[21]	Fabian J, Sarma S Das 2004 Rev. Mod. Phys. 76 323 Google Scholar
[22]	Richard P, Sato T, Nakayama K, Takahashi T, Ding H 2011 Reports Prog. Phys. 74 124512 Google Scholar
[23]	Eich S, Stange A, Carr A V, Urbancic J, Popmintchev T, Wiesenmayer M, Jansen K, Ruffing A, Jakobs S, Rohwer T, Hellmann S, Chen C, Matyba P, Kipp L, Rossnagel K, Bauer M, Murnane M M, Kapteyn H C, Mathias S, Aeschlimann M 2014 J. Electron Spectros. Relat. Phenomena 195 231 Google Scholar
[24]	Cacho C, Crepaldi A, Battiato M, Braun J, Cilento F, Zacchigna M, Richter M C, Heckmann O, Springate E, Liu Y, Dhesi S S, Berger H, Bugnon Ph, Held K, Grioni M, Ebert H, Hricovini K, Minár J, Parmigiani F 2015 Phys. Rev. Lett. 114 097401 Google Scholar
[25]	Glinka Y D, Babakiray S, Johnson T A, Holcomb M B, Lederman D 2014 Appl. Phys. Lett. 105 171905 Google Scholar
[26]	Lai Y P, Chen H J, Wu K H, Liu J M 2014 Appl. Phys. Lett. 105 232110 Google Scholar
[27]	Weis M, Balin K, Rapacz R, Nowak A, Lejman M, Szade J, Ruello P 2015 Phys. Rev. B 92 014301 Google Scholar
[28]	Sánchez-Barriga J, Battiato M, Krivenkov M, Golias E, Varykhalov A, Romualdi A, Yashina L V, Minár J, Kornilov O, Ebert H, Held K, Braun J 2017 Phys. Rev. B 95 125405 Google Scholar
[29]	李正中 2002 固体理论 (第2版) (北京:高等教育出版社) 第 40 页 Li Z Z 2002 Solid Theory (2nd Ed.) (Beijing: Higher Education Press) p40 (in Chinese)
[30]	Cheng L, La-O-Vorakiat C, Tang C S, Nair S K, Xia B, Wang L, Zhu J X, Chia Elbert E M 2014 Appl. Phys. Lett. 104 211906 Google Scholar
[31]	Pan Z H, Fedorov A V, Gardner D, Lee Y S, Chu S, Valla T 2012 Phys. Rev. Lett. 108 187001 Google Scholar
[32]	Valdés Aguilar R, Qi J, Brahlek M, Bansal N, Azad A, Bowlan J, Oh S, Taylor A J, Prasankumar R P, Yarotski D A 2015 Appl. Phys. Lett. 106 011901 Google Scholar
[33]	Wu L, Brahlek M, Aguilar R Valdés, Stier A V, Morris C M, Lubashevsky Y, Bilbro L S, Bansal N, Oh S, Armitage N P 2013 Nat. Phys. 9 410 Google Scholar
[34]	Valdés Aguilar R, Stier A V, Liu W, Bilbro L S, George D K, Bansal N, Wu L, Cerne J, Markelz A G, Oh S, Armitage N P 2012 Phys. Rev. Lett. 108 087403 Google Scholar
[35]	Choi Y G, Zhung C J, Park S H, Park J B, Kim J S, Kim S H, Park J H, Lee J S 2018 Phys. Rev. B 97 075307 Google Scholar
[36]	Wang Y H, Hsieh D, Sie E J, Steinberg H, Gardner D R, Lee Y S, Jarillo-Herrero P, Gedik N 2012 Phys. Rev. Lett. 109 127401 Google Scholar
[37]	Sobota J A, Yang S L, Leuenberger D, Kemper A F, Analytis J G, Fisher I R, Kirchmann P S, Devereaux T P, Shen Z X 2014 J. Electron Spectros. Relat. Phenomena 195 249 Google Scholar
[38]	Saha K, Garate I 2014 Phys. Rev. B 90 245418 Google Scholar
[39]	Shapourian H, Hughes T L, Ryu S 2015 Phys. Rev. B 92 165131 Google Scholar
[40]	Yazyev O V, Moore J E, Louie S G 2010 Phys. Rev. Lett. 105 266806 Google Scholar
[41]	Liu C X, Qi X L, Zhang H J, Dai X, Fang Z, Zhang S C 2010 Phys. Rev. B 82 045122 Google Scholar
[42]	Kamaraju N, Sunil K, Sood A K 2010 Europhys. Lett. 92 47007 Google Scholar
[43]	Li Y W, Stoica Vladimir A, Endicott L, Wang G Y, Uher C, Clarke R 2010 Appl. Phys. Lett. 97 171908 Google Scholar
[44]	Wang Y, Xu X, Venkatasubramanian R 2008 Appl. Phys. Lett. 93 113114 Google Scholar
[45]	Cheng T K, Vidal J, Zeiger H. J, Dresselhaus G, Dresselhaus M S, Ippen E P 1991 Appl. Phys. Lett 59 1923 Google Scholar
[46]	Richter W, Kohler H, Becker C R 1977 Phys. Status Solidi 84 619 Google Scholar
[47]	Merlin R 1997 Solid State Commun. 102 207 Google Scholar
[48]	Sobota J A, Yang S L, Leuenberger D, Kemper A F, Analytis J G, Fisher I R, Kirchmann P S, Devereaux T P, Shen Z X 2014 Phys. Rev. Lett. 113 157401 Google Scholar
[49]	Xu Y, Khafizov M, Satrapinsky L, Kúš P, Plecenik A, Sobolewski R 2003 Phys. Rev. Lett. 91 197004 Google Scholar
[50]	Taneda T, Pepe G P, Parlato L, Golubov A A, Sobolewski R 2007 Phys. Rev. B 75 174507 Google Scholar
[51]	Giraud S, Egger R 2011 Phys. Rev. B 83 245322 Google Scholar
[52]	Giraud S, Kundu A, Egger R 2012 Phys. Rev. B 85 035441 Google Scholar
[53]	Iyer V, Chen Y P, Xu X 2018 Phys. Rev. Lett. 121 026807 Google Scholar
[54]	Hertel R 2005 arXiv:cond-mat 0509 0509060
[55]	Sobota J A, Yang S L, Kemper A F, Lee J J, Schmitt F T, Li W, Moore R G, Analytis J G, Fisher I R, Kirchmann P S, Devereaux T P, Shen Z X 2013 Phys. Rev. Lett. 111 136802 Google Scholar

[1]	张帅, 宋凤麒. 拓扑绝缘体中量子霍尔效应的研究进展. , 2023, 72(17): 177302. doi: 10.7498/aps.72.20230698
[2]	刘畅, 王亚愚. 磁性拓扑绝缘体中的量子输运现象. , 2023, 72(17): 177301. doi: 10.7498/aps.72.20230690
[3]	刘浪, 王一平. 基于可调频光力晶格中声子-光子拓扑性质的模拟和探测. , 2022, 71(22): 224202. doi: 10.7498/aps.71.20221286
[4]	贾亮广, 刘猛, 陈瑶瑶, 张钰, 王业亮. 单层二维量子自旋霍尔绝缘体1T'-WTe₂研究进展. , 2022, 71(12): 127308. doi: 10.7498/aps.71.20220100
[5]	许佳玲, 贾利云, 刘超, 吴佺, 赵领军, 马丽, 侯登录. Li(Na)AuS体系拓扑绝缘体材料的能带结构. , 2021, 70(2): 027101. doi: 10.7498/aps.70.20200885
[6]	郭志超, 张桐耀, 张靖. 微米气室铯原子自旋噪声谱. , 2020, 69(3): 037201. doi: 10.7498/aps.69.20191623
[7]	王航天, 赵海慧, 温良恭, 吴晓君, 聂天晓, 赵巍胜. 高性能太赫兹发射: 从拓扑绝缘体到拓扑自旋电子. , 2020, 69(20): 200704. doi: 10.7498/aps.69.20200680
[8]	贾鼎, 葛勇, 袁寿其, 孙宏祥. 基于蜂窝晶格声子晶体的双频带声拓扑绝缘体. , 2019, 68(22): 224301. doi: 10.7498/aps.68.20190951
[9]	刘畅, 刘祥瑞. 强三维拓扑绝缘体与磁性拓扑绝缘体的角分辨光电子能谱学研究进展. , 2019, 68(22): 227901. doi: 10.7498/aps.68.20191450
[10]	黄瑞, 李春, 金蔚, GeorgiosLefkidis, WolfgangHübner. 双磁性中心内嵌富勒烯Y₂C₂@C₈₂-C₂(1)中的超快自旋动力学行为. , 2019, 68(2): 023101. doi: 10.7498/aps.68.20181887
[11]	敬玉梅, 黄少云, 吴金雄, 彭海琳, 徐洪起. 三维拓扑绝缘体antidot阵列结构中的磁致输运研究. , 2018, 67(4): 047301. doi: 10.7498/aps.67.20172346
[12]	高艺璇, 张礼智, 张余洋, 杜世萱. 二维有机拓扑绝缘体的研究进展. , 2018, 67(23): 238101. doi: 10.7498/aps.67.20181711
[13]	李兆国, 张帅, 宋凤麒. 拓扑绝缘体的普适电导涨落. , 2015, 64(9): 097202. doi: 10.7498/aps.64.097202
[14]	王青, 盛利. 磁场中的拓扑绝缘体边缘态性质. , 2015, 64(9): 097302. doi: 10.7498/aps.64.097302
[15]	陈艳丽, 彭向阳, 杨红, 常胜利, 张凯旺, 钟建新. 拓扑绝缘体Bi2Se3中层堆垛效应的第一性原理研究. , 2014, 63(18): 187303. doi: 10.7498/aps.63.187303
[16]	李平原, 陈永亮, 周大进, 陈鹏, 张勇, 邓水全, 崔雅静, 赵勇. 拓扑绝缘体Bi2Te3的热膨胀系数研究. , 2014, 63(11): 117301. doi: 10.7498/aps.63.117301
[17]	张小明, 刘国栋, 杜音, 刘恩克, 王文洪, 吴光恒, 柳忠元. 半Heusler型拓扑绝缘体LaPtBi能带调控的研究. , 2012, 61(12): 123101. doi: 10.7498/aps.61.123101
[18]	曾伦武, 张浩, 唐中良, 宋润霞. 拓扑绝缘体椭球粒子的电磁散射. , 2012, 61(17): 177303. doi: 10.7498/aps.61.177303
[19]	曾伦武, 宋润霞. 点电荷在拓扑绝缘体和导体中感应磁单极. , 2012, 61(11): 117302. doi: 10.7498/aps.61.117302
[20]	贺雪鹏, 刘院省, 刘世炳. 超快激光抽运-探测中探针光时间延迟量的实时测量原理与光学设计. , 2011, 60(2): 024212. doi: 10.7498/aps.60.024212

计量

文章访问数: 13406
PDF下载量: 459
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

拓扑绝缘体中的超快电荷自旋动力学