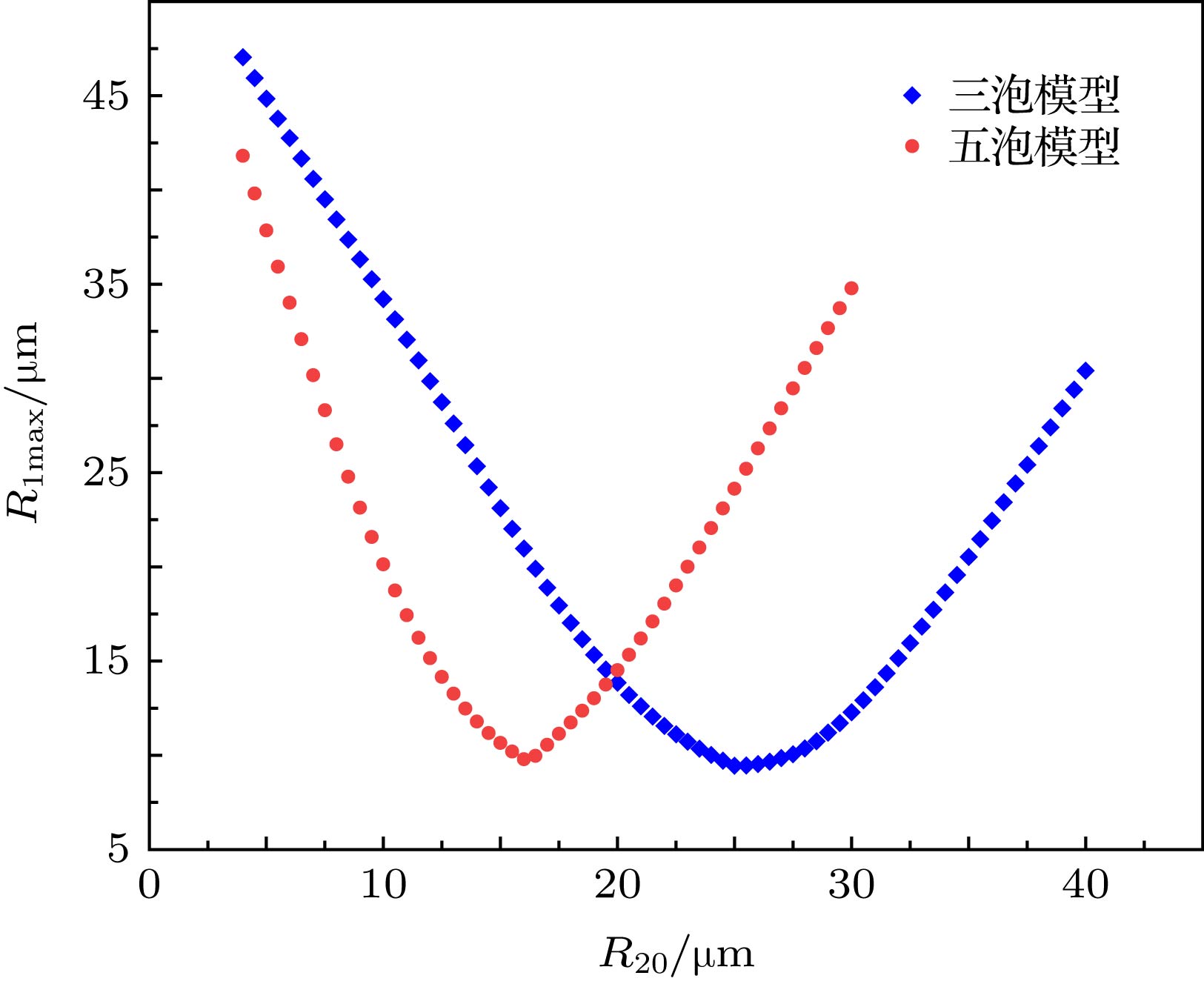
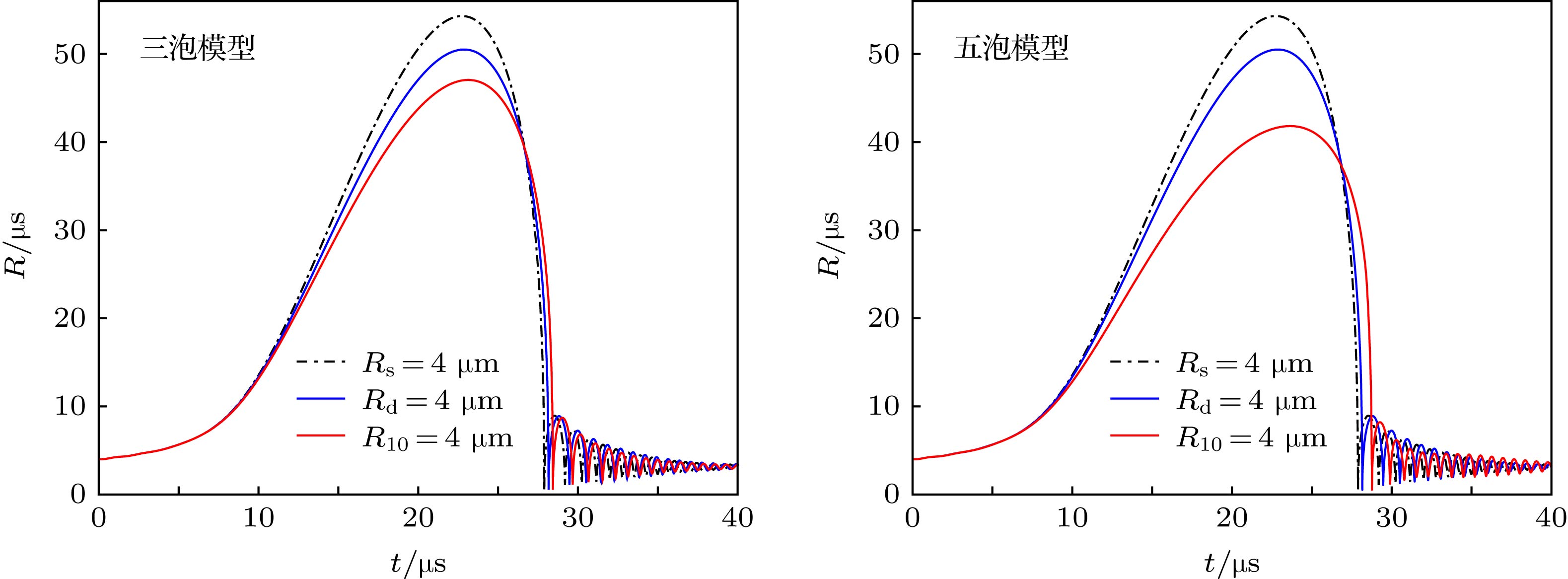
-
依据超声场下形成的空化多泡的形状结构, 建立了两种简化的多泡模型, 即三泡模型和五泡模型, 并利用考虑气泡之间相互作用和液体可压缩性的非线性Keller-Miksis方程, 数值研究了三泡和五泡模型中周围大气泡对中间小气泡空化效应的影响. 结果表明, 在适当条件下随着周围大气泡半径的逐渐增大, 中间小气泡会被完全抑制或会发生延迟膨胀现象. 延迟膨胀的小气泡崩溃时的泡内温度, 当周围大气泡数适当多时, 可以高于相同初始半径的单泡泡内温度. 大小气泡之间的次Bjerknes力在小气泡延迟膨胀时表现为先排斥后吸引, 而正常膨胀大小气泡之间的次Bjerknes力两次都是吸引力.
-
关键词:
- 多泡模型 /
- 延迟膨胀 /
- 泡内温度 /
- 次Bjerknes力
In previous papers, researchers generally adopted a simplified assumption that there is a single type of bubble in liquid. In this paper, two simplified bubbles models are established based on the shape and structure of cavitation bubbles formed in ultrasonic field, i.e. linear model consisting of three bubbles and cluster model composed of five bubbles, and each model is assumed to consist of two types of bubbles. The influences of large bubbles on cavitation effect of small bubble in the middle for three- and five-bubble model are numerically studied by using the modified Keller-Miksis equation and van der Waals equation. The changes of the expansion radius of the small bubble in the middle, the temperature in the small bubble and the secondary Bjerknes force between large bubble and small bubble with the increase of the initial radius of large bubbles are mainly investigated. In the calculation, it is assumed that the locations of bubbles stay unchanged and the shape of bubbles remains spherical in the oscillation process. Meanwhile, the time-delay effect on the secondary Bjerknes force can be neglected because the sound wave speed is very fast in water and the bubbles in the liquid can oscillate synchronously. The calculation results show that the expansion of small bubble in the middle can be completely suppressed or delayed when the initial radius and the number of bubbles are appropriate on condition that the distance between large and small bubble, the driving sound pressure and frequency of the applied sound field stay unchanged. The main reason for delayed expansion is that the total pressure acting on small bubbles is delayed to form a negative pressure in the process of the change. The collapse time of delayed expansion of small bubble is basically the same as that of large bubbles, which makes small bubble collapsed rapidly and thoroughly under the strong radiative barotropic effect of large bubble's collapse, and leads the maximum temperature in the small bubble to be higher than that of the single bubble with the same initial radius and the small bubble with normal expansion. In addition, when the expansion of small bubble is delayed, the secondary Bjerknes force between the large bubble and the small bubble appears to be repulsive first and attractive then. This rule is different from the change rule of the secondary Bjerknes force between the two bubbles in normal expansion. The results in this paper have significant theoretical guidance for specific problems such as suppressing liquid cavitation or enhancing liquid cavitation effect by the manual injection of large bubbles.[1] Yasui K, Iida Y, Tuziuti T, Kozuka T, Towata A 2008 Phys. Rev. E 77 016609
Google Scholar
[2] Doinikov A A, Zavtrak S T 1998 J. Acoust. Soc. Am. 99 3849
[3] Moussatov A, Granger C, Dubus B 2003 Ultrason. Sonochem. 10 191
Google Scholar
[4] Mettin R, Luther S, Ohl C D, Lauterborn W 1999 Ultrason. Sonochem. 6 25
Google Scholar
[5] Cr um, Lawrence A 1975 J. Acoust. Soc. Am. 57 1363
Google Scholar
[6] Mettin R, Akhatov I, Parlitz U, Ohl C D, Lauterborn W 1997 Phys. Rev. E 56 2924
Google Scholar
[7] 卢义刚, 吴雄慧 2011 60 046202
Google Scholar
Lu Y G, Wu X H 2011 Acta Phys. Sin. 60 046202
Google Scholar
[8] Jiang L, Liu F, Chen H, Chen H S, Wang J D, Chen D R 2012 Phys. Rev. E 85 036312
Google Scholar
[9] Ida M, Naoe T, Futakawa M 2007 Phys. Rev. E 76 046309
Google Scholar
[10] 蒲中奇, 张伟, 施克仁, 张俊华, 吴玉林 2005 清华大学学报: 自然科学版 45 1450
Google Scholar
Pu Z Q, Zhang W, Shi K R, Zhang J H, Wu Y L 2005 Journal Tsinghua University (Science and Technology) 45 1450
Google Scholar
[11] 王德鑫, 那仁满都拉 2018 67 037802
Google Scholar
Wang D X, Naranmandula 2018 Acta Phys. Sin. 67 037802
Google Scholar
[12] 马艳, 林书玉, 徐洁, 唐一璠 2017 66 014302
Google Scholar
Ma Y, Lin S Y, Xu J, Tang Y F 2017 Acta Phys. Sin. 66 014302
Google Scholar
[13] 王成会, 莫润阳, 胡静, 陈时 2015 64 234301
Google Scholar
Wang C H, Mo R Y, Hu J, Chen S 2015 Acta Phys. Sin. 64 234301
Google Scholar
[14] An Y 2011 Phys. Rev. E 83 066313
Google Scholar
[15] 苗博雅, 安宇 2015 64 204301
Google Scholar
Miao B Y, An Y 2015 Acta Phys. Sin. 64 204301
Google Scholar
[16] Nasibullaeva E S, Akhatov I S 2013 J. Acoust. Soc. Am. 133 3727
Google Scholar
[17] 陈时, 张迪, 王成会, 张引红 2019 68 074301
Google Scholar
Chen S, Zhang D, Wang C H, Zhang Y H 2019 Acta Phys. Sin. 68 074301
Google Scholar
[18] Zhang Y Y, Chen W Z, Zhang L L, Wang X, Chen Z 2019 Chin. Phys. Lett. 36 034301
Google Scholar
[19] Wu W H, Yang P F, Zhai W, Wei B B 2019 Chin. Phys. Lett. 36 084302
Google Scholar
[20] Zhu C S, Han D, Feng L, Xu S 2019 Chin. Phys. B 28 034701
Google Scholar
[21] 王成会, 林书玉 2011 声学学报 36 325
Google Scholar
Wang C H, Lin S Y 2011 Acta Acustica 36 325
Google Scholar
[22] Jiao J J, He Y, Yasui K, Kentish S E, Ashokkumar M, Manasseh R, Lee J 2015 Ultrason. Sonochem. 22 70
Google Scholar
[23] Hilgenfeldt S, Grossmann S, LohseD 1999 Phys. Fluids 11 1318
Google Scholar
-
图 2 小气泡最大膨胀半径随大气泡初始半径的变化
Fig. 2. The maximum expansion radius of small bubbles varies with the initial radius of large bubbles
图 3 均匀气泡系统中中间气泡半径随时间的变化曲线
Fig. 3. Radius-time curves of middle bubbles in uniform bubble system
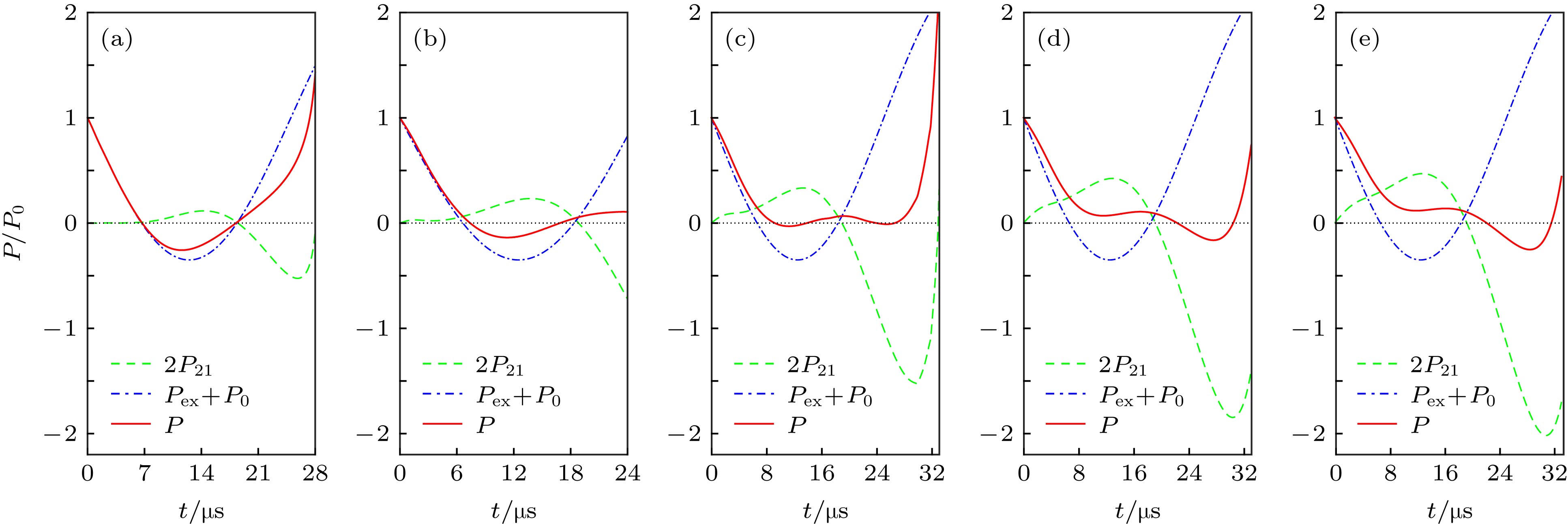
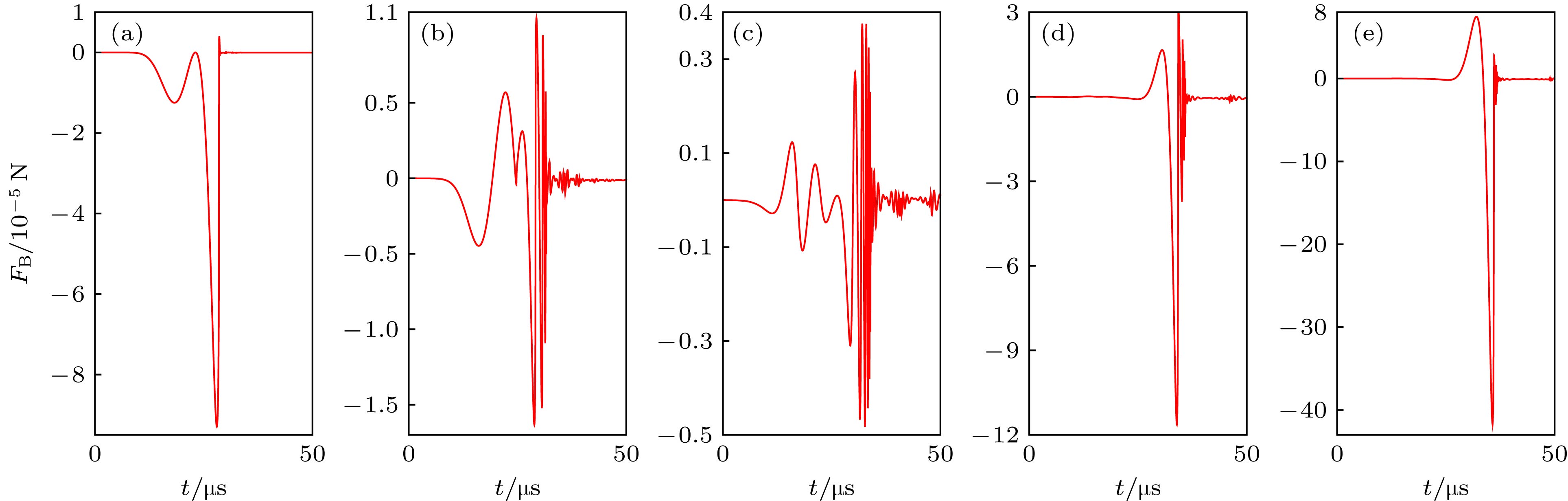
图 5 三泡模型中小气泡膨胀阶段受到的压强 (a)
$R_{20}=5\;{\text{μm}}$ ; (b)$R_{20}=15\;{\text{μm}}$ ; (c)$R_{20}=25\;{\text{μm}}$ ; (d)$R_{20}=35\;{\text{μm}}$ ; (e)$R_{20}=40\;{\text{μm}}$ Fig. 5. Total pressure acting on growth stage of small bubble in three-bubble model: (a)
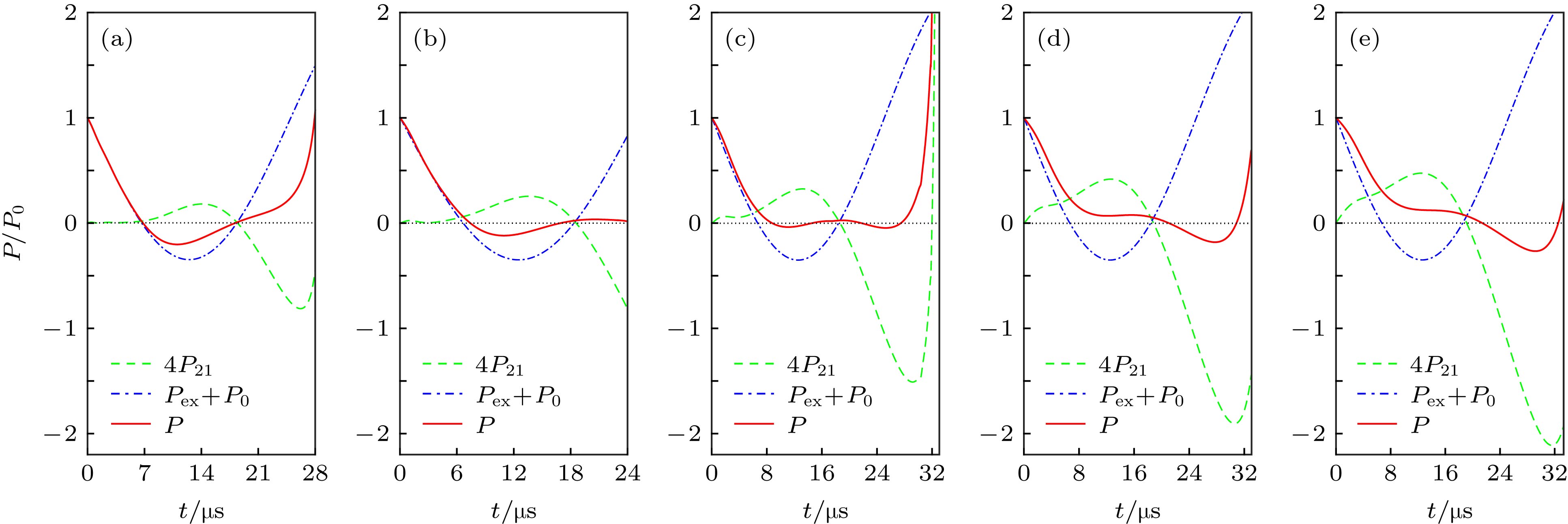
$R_{20}=5\;{\text{μm}}$ ; (b)$R_{20}=15\;{\text{μm}}$ ; (c)$R_{20}=25\;{\text{μm}}$ ; (d)$R_{20}=35\;{\text{μm}}$ ; (e)$R_{20}=40\;{\text{μm}}$ .
图 6 五泡模型中小气泡膨胀阶段受到的压强 (a)
$R_{20}=5\;{\text{μm}}$ ; (b)$R_{20}=10\;{\text{μm}}$ ; (c)$R_{20}=16\;{\text{μm}}$ ; (d)$R_{20}=25\;{\text{μm}}$ ; (e)$R_{20}=30\;{\text{μm}}$ Fig. 6. Total pressure acting on growth stage of small bubble in five-bubble model: (a)
$R_{20}=5\;{\text{μm}}$ ; (b)$R_{20}=10\;{\text{μm}}$ ; (c)$R_{20}=16\;{\text{μm}}$ ; (d)$R_{20}=25\;{\text{μm}}$ ; (e)$R_{20}=30\;{\text{μm}}$ .
图 7 两个模型中小气泡内的最高温度随大气泡初始半径的变化
Fig. 7. The maximum temperature of small bubbles in two models varies with the initial radius of large bubbles
图 8 三泡模型中大小气泡之间的次Bjerknes力的变化 (a)
$R_{20}=5\;{\text{μm}}$ ; (b)$R_{20}=15\;{\text{μm}}$ ; (c)$R_{20}=25\;{\text{μm}}$ ; (d)$R_{20}=35\;{\text{μm}}$ ; (e)$R_{20}=40\;{\text{μm}}$ Fig. 8. Changes of secondary Bjerknes forces between large and small bubbles in three-bubble model: (a)
$R_{20}=5\;{\text{μm}}$ ; (b)$R_{20}=15\;{\text{μm}}$ ; (c)$R_{20}=25\;{\text{μm}}$ ; (d)$R_{20}=35\;{\text{μm}}$ ; (e)$R_{20}=40\;{\text{μm}}$ .
图 9 五泡模型中大小气泡之间的次Bjerknes力的变化 (a)
$R_{20}=5\;{\text{μm}}$ ; (b)$R_{20}=10\;{\text{μm}}$ ; (c)$R_{20}=16\;{\text{μm}}$ ; (d)$R_{20}=25\;{\text{μm}}$ ; (e)$R_{20}=30\;{\text{μm}}$ Fig. 9. Changes of secondary Bjerknes forces between large and small bubbles in five-bubble model: (a)
$R_{20}=5\;{\text{μm}}$ ; (b)$R_{20}=10\;{\text{μm}}$ ; (c)$R_{20}=16\;{\text{μm}}$ ; (d)$R_{20}=25\;{\text{μm}}$ ; (e)$R_{20}=30\;{\text{μm}}$ . -
[1] Yasui K, Iida Y, Tuziuti T, Kozuka T, Towata A 2008 Phys. Rev. E 77 016609
Google Scholar
[2] Doinikov A A, Zavtrak S T 1998 J. Acoust. Soc. Am. 99 3849
[3] Moussatov A, Granger C, Dubus B 2003 Ultrason. Sonochem. 10 191
Google Scholar
[4] Mettin R, Luther S, Ohl C D, Lauterborn W 1999 Ultrason. Sonochem. 6 25
Google Scholar
[5] Cr um, Lawrence A 1975 J. Acoust. Soc. Am. 57 1363
Google Scholar
[6] Mettin R, Akhatov I, Parlitz U, Ohl C D, Lauterborn W 1997 Phys. Rev. E 56 2924
Google Scholar
[7] 卢义刚, 吴雄慧 2011 60 046202
Google Scholar
Lu Y G, Wu X H 2011 Acta Phys. Sin. 60 046202
Google Scholar
[8] Jiang L, Liu F, Chen H, Chen H S, Wang J D, Chen D R 2012 Phys. Rev. E 85 036312
Google Scholar
[9] Ida M, Naoe T, Futakawa M 2007 Phys. Rev. E 76 046309
Google Scholar
[10] 蒲中奇, 张伟, 施克仁, 张俊华, 吴玉林 2005 清华大学学报: 自然科学版 45 1450
Google Scholar
Pu Z Q, Zhang W, Shi K R, Zhang J H, Wu Y L 2005 Journal Tsinghua University (Science and Technology) 45 1450
Google Scholar
[11] 王德鑫, 那仁满都拉 2018 67 037802
Google Scholar
Wang D X, Naranmandula 2018 Acta Phys. Sin. 67 037802
Google Scholar
[12] 马艳, 林书玉, 徐洁, 唐一璠 2017 66 014302
Google Scholar
Ma Y, Lin S Y, Xu J, Tang Y F 2017 Acta Phys. Sin. 66 014302
Google Scholar
[13] 王成会, 莫润阳, 胡静, 陈时 2015 64 234301
Google Scholar
Wang C H, Mo R Y, Hu J, Chen S 2015 Acta Phys. Sin. 64 234301
Google Scholar
[14] An Y 2011 Phys. Rev. E 83 066313
Google Scholar
[15] 苗博雅, 安宇 2015 64 204301
Google Scholar
Miao B Y, An Y 2015 Acta Phys. Sin. 64 204301
Google Scholar
[16] Nasibullaeva E S, Akhatov I S 2013 J. Acoust. Soc. Am. 133 3727
Google Scholar
[17] 陈时, 张迪, 王成会, 张引红 2019 68 074301
Google Scholar
Chen S, Zhang D, Wang C H, Zhang Y H 2019 Acta Phys. Sin. 68 074301
Google Scholar
[18] Zhang Y Y, Chen W Z, Zhang L L, Wang X, Chen Z 2019 Chin. Phys. Lett. 36 034301
Google Scholar
[19] Wu W H, Yang P F, Zhai W, Wei B B 2019 Chin. Phys. Lett. 36 084302
Google Scholar
[20] Zhu C S, Han D, Feng L, Xu S 2019 Chin. Phys. B 28 034701
Google Scholar
[21] 王成会, 林书玉 2011 声学学报 36 325
Google Scholar
Wang C H, Lin S Y 2011 Acta Acustica 36 325
Google Scholar
[22] Jiao J J, He Y, Yasui K, Kentish S E, Ashokkumar M, Manasseh R, Lee J 2015 Ultrason. Sonochem. 22 70
Google Scholar
[23] Hilgenfeldt S, Grossmann S, LohseD 1999 Phys. Fluids 11 1318
Google Scholar
下载:
计量
- 文章访问数: 9055
- PDF下载量: 171
- 被引次数: 0
