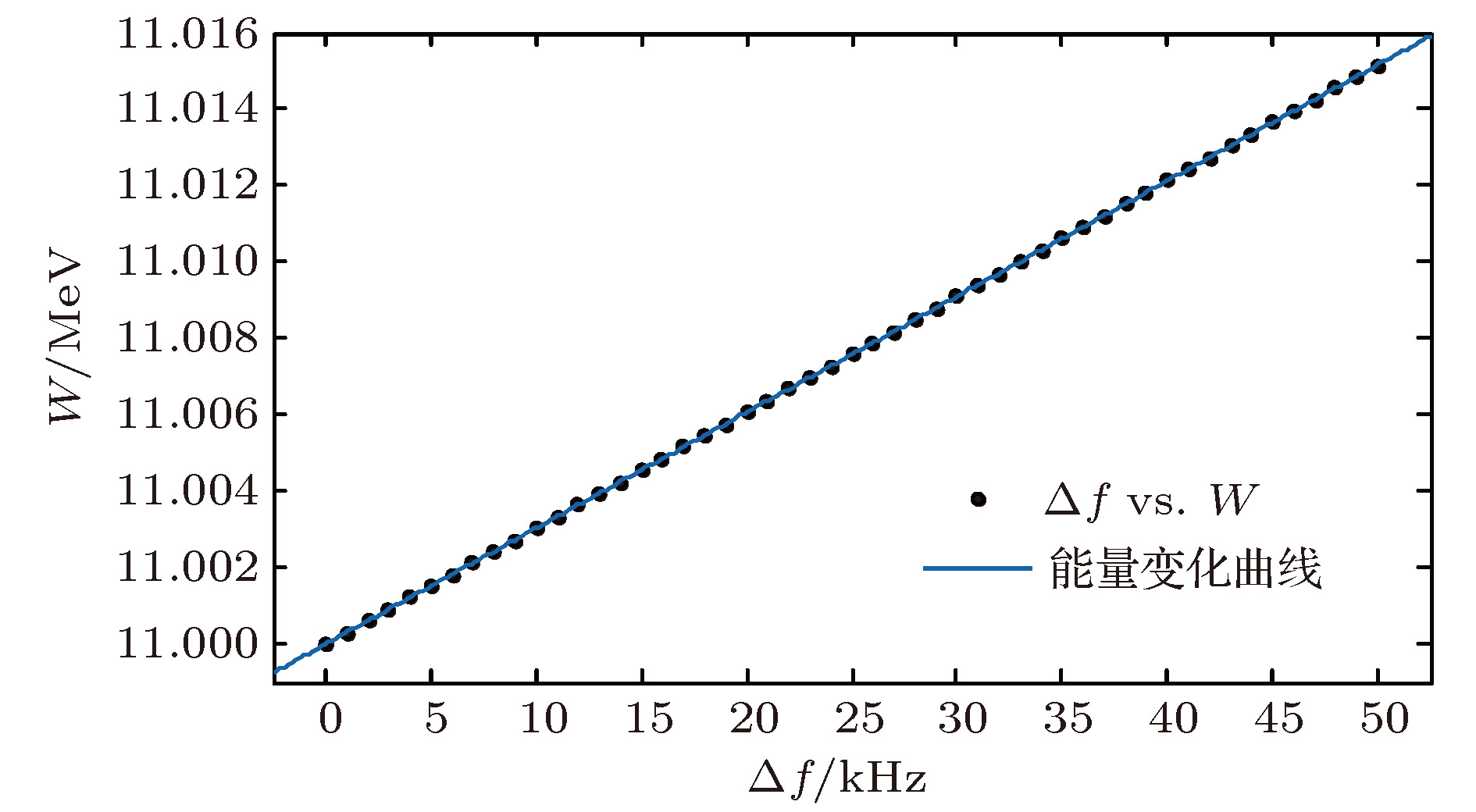
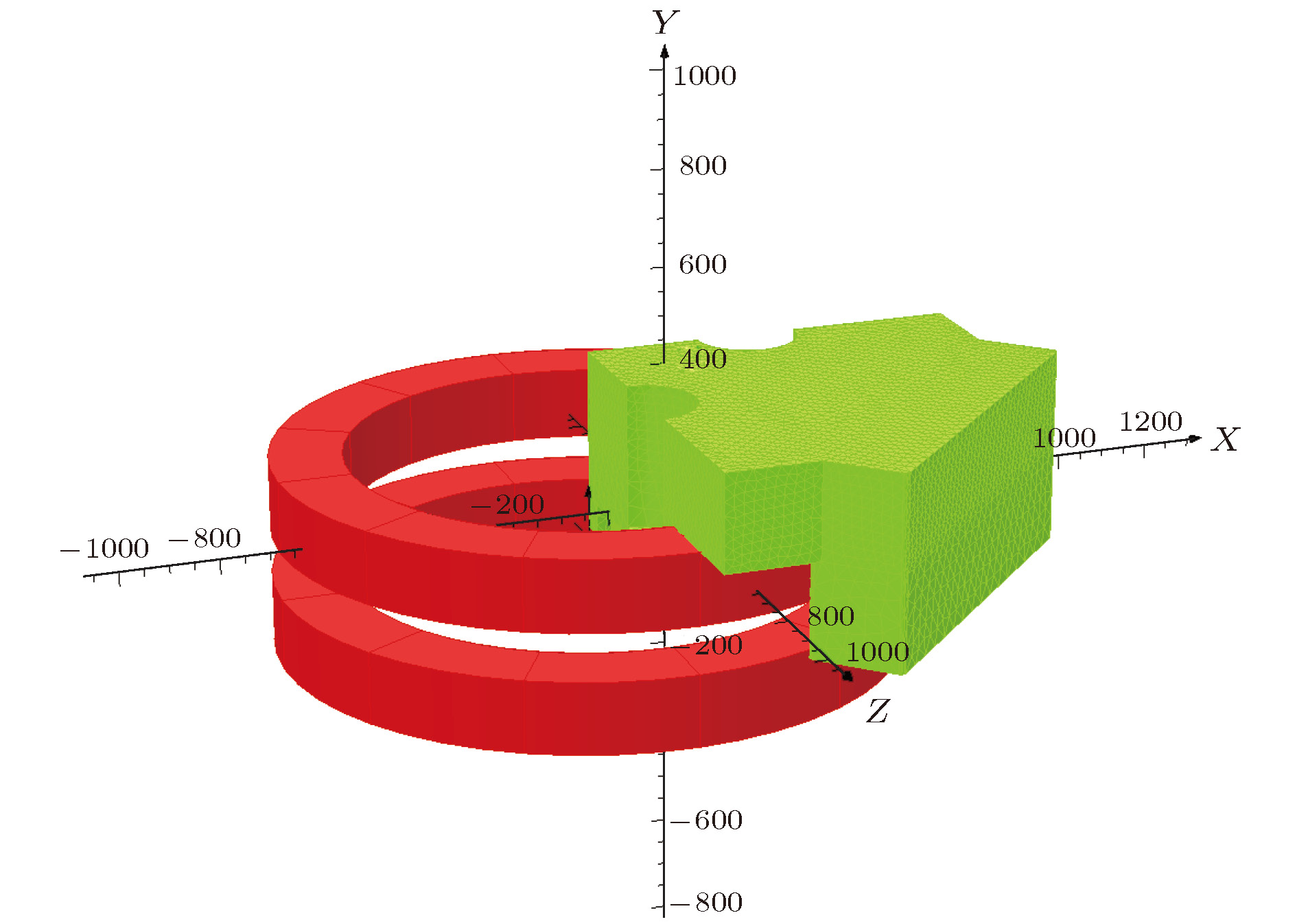
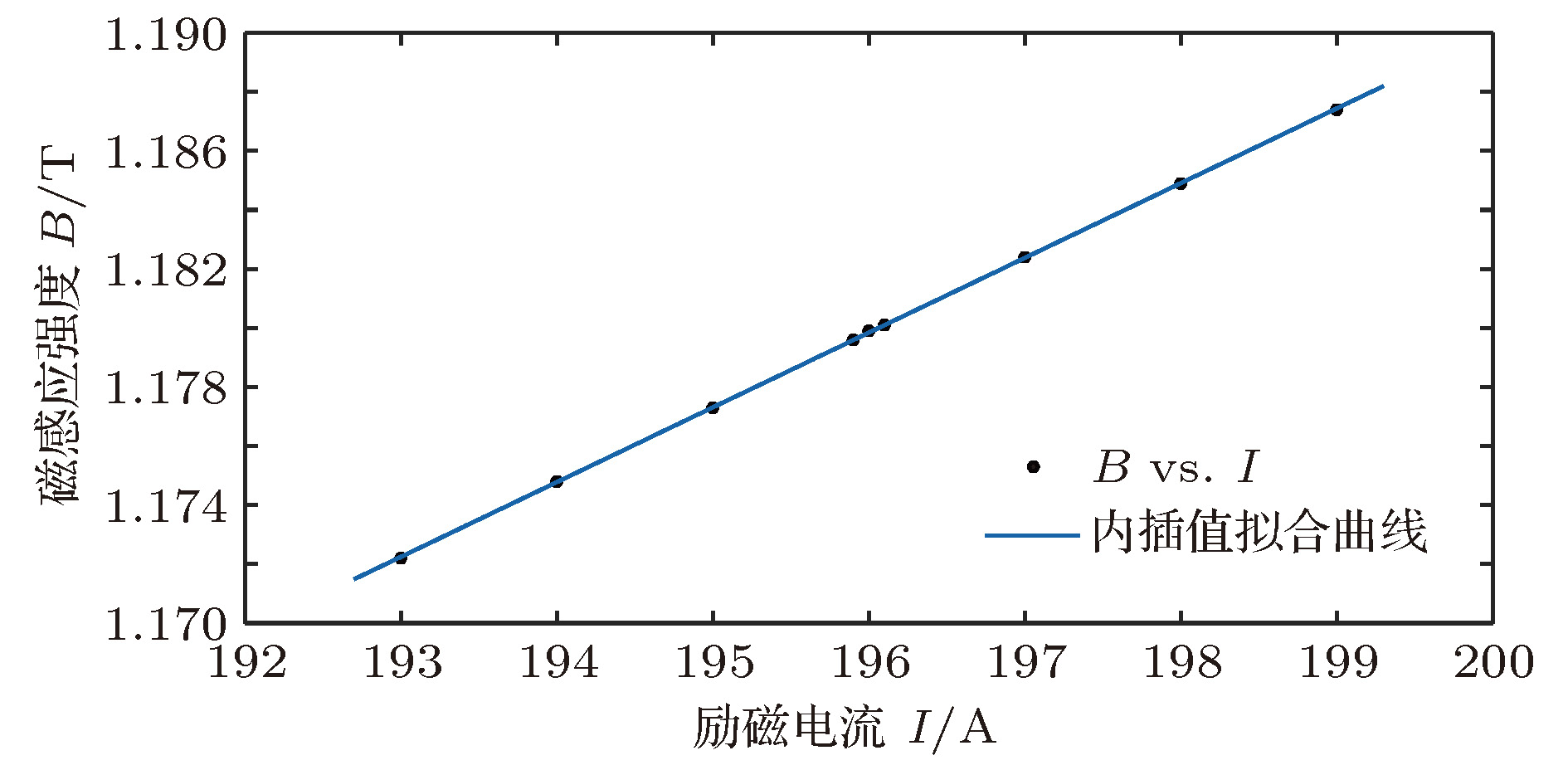
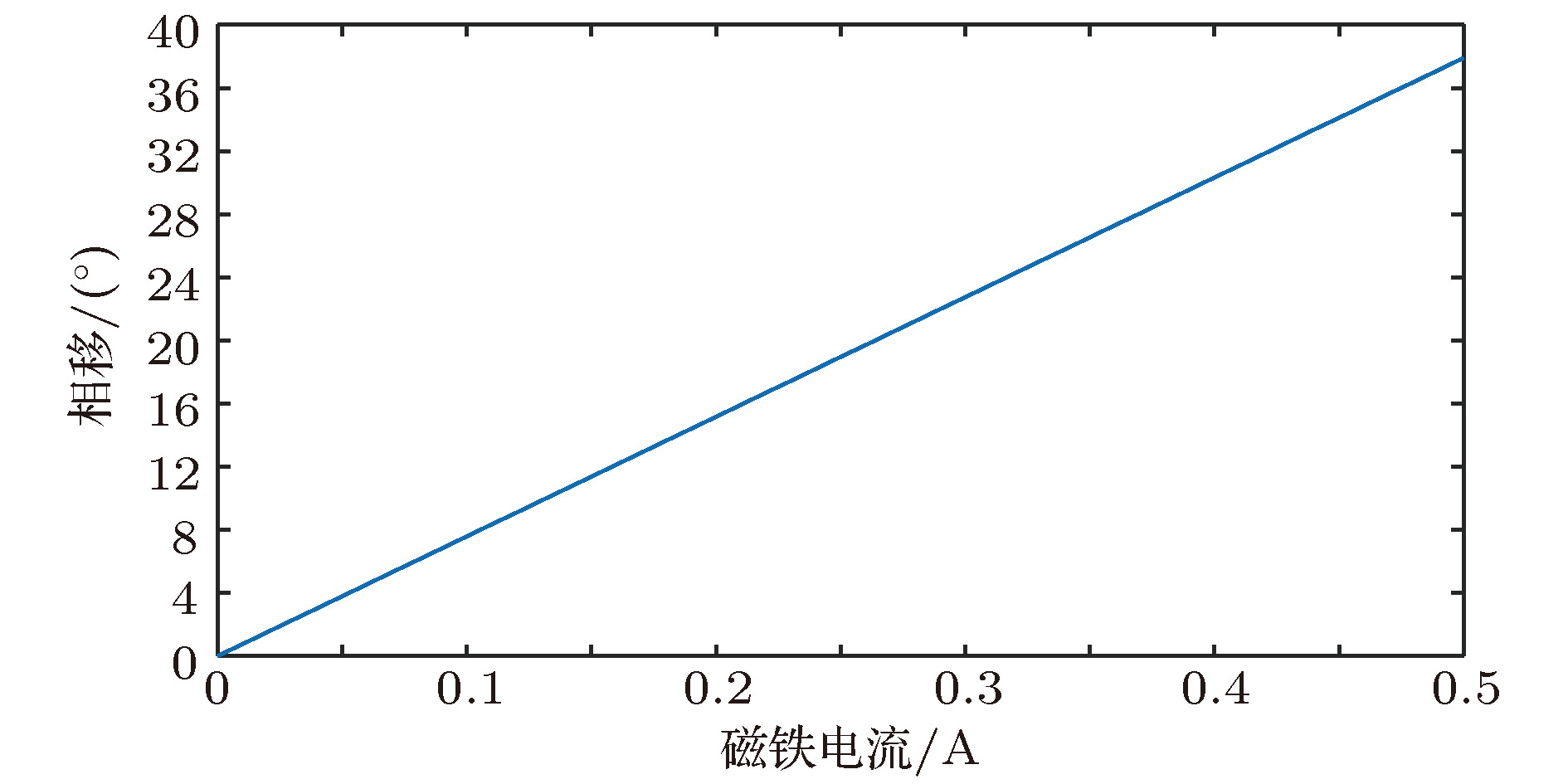
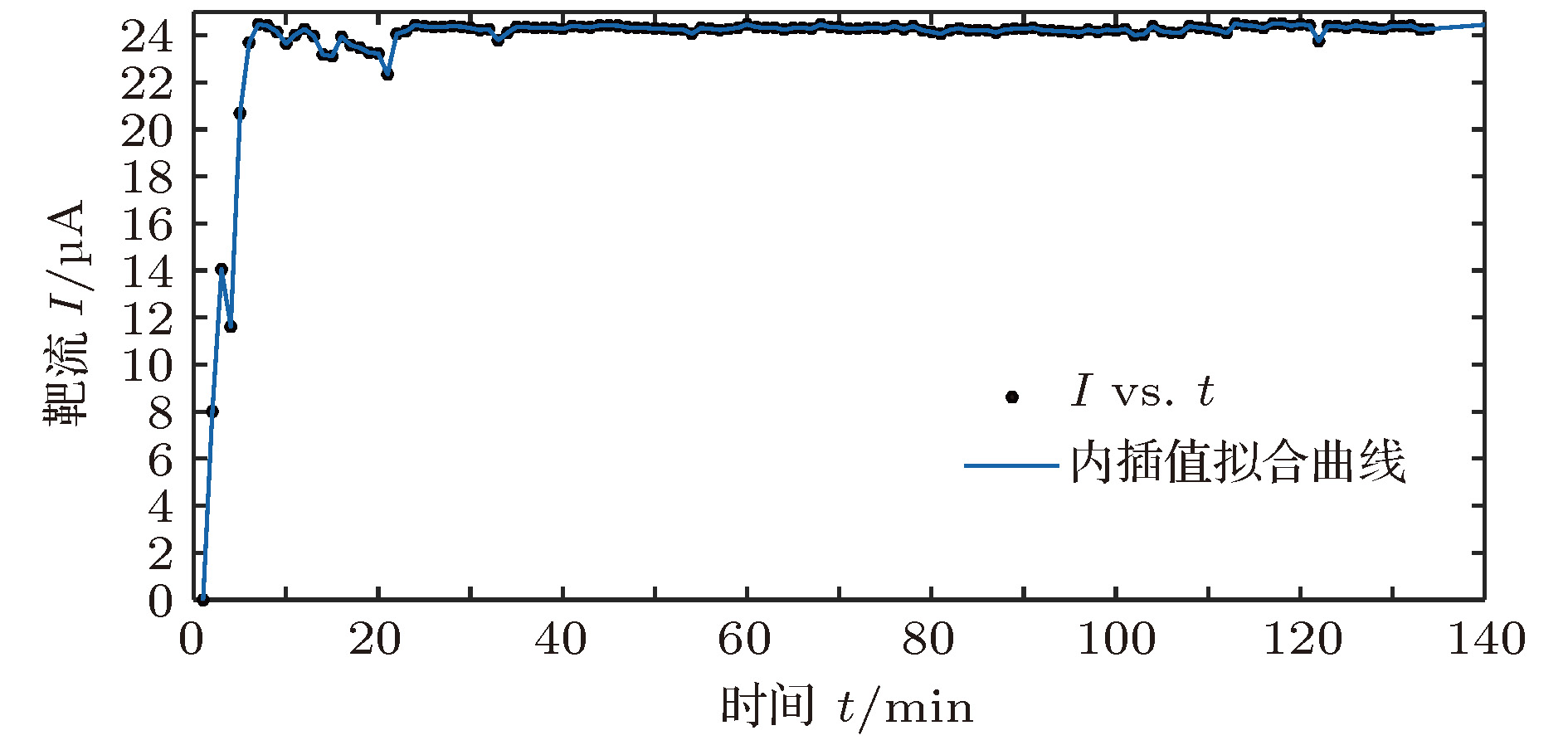
-
高频谐振腔在回旋加速器实际运行过程中受束流负载、重力和热损耗引起的腔体变形等因素的影响, 其谐振频率会发生一定的偏移, 导致高频工作频率会随着谐振腔的谐振频率而变化. 为满足等时性加速的要求, 当高频工作频率发生改变时磁场强度也应进行相应的变化, 即励磁电流的大小需要相应改变, 使得粒子回旋频率与高频谐振频率相匹配以克服滑相. 首先通过有限元仿真软件建立静磁场模型模拟不同励磁电流下回旋加速器的平均磁场, 然后理论分析磁场与谐振频率的关系, 最后得到励磁电流在小区间变化时与谐振频率的关系; 根据计算的不同谐振频率对应的最佳励磁电流, 完成励磁电流的自动跟频. 在保证最大碳膜束流的情况下, 实验得到不同谐振频率对应的最佳励磁电流, 使理论得以验证. 根据其关系实现了励磁电流自动调节, 克服了滑相, 保证了法拉第束流的稳定输出. 该方法使得励磁电流能够快速、准确地寻找并跟踪谐振腔频率, 克服了频率偏移导致的滑相, 完成束流的稳定输出.The high-frequency resonant cavity is affected by factors such as beam load, gravity and heat loss caused by cavity deformation during the actual operation of the medical cyclotron. The resonant frequency will shift to a certain extent, resulting in the high-frequency operation frequency varying with the resonant frequency of the resonator cavity. In order to meet the requirements for isochronous acceleration, the magnetic field strength should also be changed correspondingly when the high-frequency operation frequency changes, that is, the magnitude of the magnet current needs changing accordingly, so that the particle cyclotron frequency matches the high-frequency resonant frequency to overcome the sliding phase. Firstly, the static magnetic field model is established by finite element simulation software to simulate the average magnetic field of cyclotron under different magnet currents. Then the relationship between the magnetic field and the resonant frequency is theoretically analyzed. Finally, the relationship between the magnet current and the resonant frequency is obtained when the magnet current varies in a small interval. According to the optimal magnet current corresponding to different resonance frequencies, the automatic frequency tracking of magnet current is completed. In the case of ensuring the maximum carbon film beam, the optimal magnet current corresponding to different resonance frequencies is obtained, which makes the theory validated. According to the relationship, the magnet current is automatically adjusted, which overcomes the slip phase and ensures the stable output of the Faraday beam. The method enables the magnet current to be quickly and accurately find and track the cavity frequency, overcomes the slip phase caused by the frequency offset, and completes the stable output of the beam.
-
Keywords:
- high frequency cavity /
- resonant frequency /
- frequency tracking /
- stable beam output
[1] Gambhir S S, Czernin J, Schwimmer J 2001 J. Nucl. Med. 42 1S
[2] Reske S N, Kotzerke J 2001 Eur. J. Nucl. Med. Mol. I. 28 1707
Google Scholar
[3] 樊明武 2000 中国工程科学 2 9
Google Scholar
Fan M W 2000 Engineering 2 9
Google Scholar
[4] Bertrand S, Vaneycken I, Lahoutte T, Covens P, Caveliers V, Kral E, Geets J M, Nactergal B, Ghyoot M, Devillet F 2018 J. Nucl. Med. 59 2106
[5] 张锦明, 田嘉禾 2006 同位素 19 241
Zhang J M, Tian J H 2006 Journal of Isotopes 19 241
[6] 赵籍九, 尹兆升 2006 粒子加速器技术 (北京: 高等教育出版社) 第236页
Zhao J J, Yin Z S 2006 Particle Accelerator Technology (Beijing: Higher Education Press) p236 (in Chinese)
[7] 陈佳洱 1993 加速器物理基础 (北京: 原子能出版社) 第20, 21页
Chen J E 1993 Basics of Accelerator Physics (Beijing: Atomic Energy Press) pp20, 21 (in Chinese)
[8] 赵凯, 牟宗信, 张家良 2014 63 185208
Google Scholar
Zhao K, Mu Z X, Zhang J L 2014 Acta Phys. Sin. 63 185208
Google Scholar
[9] 张天爵, 李振国, 储诚节 2010 科学通报 35 3351
Zhang T J, Li Z G, Chu C J 2010 Science Bulletin 35 3351
[10] 雷钰 2012 硕士学位论文 (成都: 成都理工大学)
Lei Yu 2012 M. S. Thesis (Chengdu: Chengdu University of Technology) (in Chinese)
[11] 答嘉曦, 洪越明, 董天临 2006 2005'全国微波毫米波会议论文集 (第三册) 中国 深圳, 2月27日−3月2日, 2006 pp64−67
Da J X, Hong Y M, Dong T L 2006 2005' National Microwave and Millimeter Wave Conference Papers Collection (Vol.3) Shenzhen, China, February 27−March 2, 2006 pp64−67 (in Chinese)
[12] 答嘉曦 2006 硕士学位论文 (武汉: 华中科技大学)
Da J X 2006 M. S. Thesis (Wuhan: Huazhong University of Science and Technology) (in Chinese)
[13] 刘毅 2008 硕士学位论文 (武汉: 华中科技大学)
Liu Yi 2008 M. S. Thesis (Wuhan: Huazhong University of Science and Technology) (in Chinese)
[14] 田瑞霞, 王贤武, 金鹏 2014 强激光与粒子束 26 26105101
Google Scholar
Tian R X, Wang X W, Jin P 2014 High Power Laser and Particle Beam 26 26105101
Google Scholar
[15] 郝焕锋 2014 博士学位论文 (北京: 中国科学院大学)
Hao H F 2014 Ph.D. Dissertation (Beijing: University of Chinese Academy of Sciences) (in Chinese)
[16] 何小中, 杨国君, 龙继东 2014 核技术 37 10201
Google Scholar
He X Z, Yang G J, Long J D 2014 Nuclear Technol. 37 10201
Google Scholar
[17] Bhandari S, Lee G H, Klales A, Watanabe K, Taniguchi T, Heller E, Kim P, Westervelt R M 2016 Nano Lett. 16 1690
Google Scholar
[18] Xia W L, Wang Z, Lu Y R 2014 IEEE Trans. Nucl. Sci. 61 2345
Google Scholar
[19] 李平, 黄娴, 文玉梅 2012 61 137504
Google Scholar
Li P, Huang X, Wen YM 2012 Acta Phys. Sin. 61 137504
Google Scholar
[20] 李毅, 王秋良 2016 Opera3D工程电磁场计算及多场耦合分析 (北京: 清华大学出版社) 第3页
Li Y, Wang Q L 2016 Electromagnetic Field Calculation and Multi-field Coupling Analysis of Opera 3D Project (Beijing: Tsinghua University Press) p3
-
图 7 励磁电流与磁感应强度的关系
Fig. 7. Relation between the excitation current and the magnetic induction intensity.
图 10 谐振频率与励磁电流的对应关系
Fig. 10. Corresponding relation between resonant frequency and magnet current.
-
[1] Gambhir S S, Czernin J, Schwimmer J 2001 J. Nucl. Med. 42 1S
[2] Reske S N, Kotzerke J 2001 Eur. J. Nucl. Med. Mol. I. 28 1707
Google Scholar
[3] 樊明武 2000 中国工程科学 2 9
Google Scholar
Fan M W 2000 Engineering 2 9
Google Scholar
[4] Bertrand S, Vaneycken I, Lahoutte T, Covens P, Caveliers V, Kral E, Geets J M, Nactergal B, Ghyoot M, Devillet F 2018 J. Nucl. Med. 59 2106
[5] 张锦明, 田嘉禾 2006 同位素 19 241
Zhang J M, Tian J H 2006 Journal of Isotopes 19 241
[6] 赵籍九, 尹兆升 2006 粒子加速器技术 (北京: 高等教育出版社) 第236页
Zhao J J, Yin Z S 2006 Particle Accelerator Technology (Beijing: Higher Education Press) p236 (in Chinese)
[7] 陈佳洱 1993 加速器物理基础 (北京: 原子能出版社) 第20, 21页
Chen J E 1993 Basics of Accelerator Physics (Beijing: Atomic Energy Press) pp20, 21 (in Chinese)
[8] 赵凯, 牟宗信, 张家良 2014 63 185208
Google Scholar
Zhao K, Mu Z X, Zhang J L 2014 Acta Phys. Sin. 63 185208
Google Scholar
[9] 张天爵, 李振国, 储诚节 2010 科学通报 35 3351
Zhang T J, Li Z G, Chu C J 2010 Science Bulletin 35 3351
[10] 雷钰 2012 硕士学位论文 (成都: 成都理工大学)
Lei Yu 2012 M. S. Thesis (Chengdu: Chengdu University of Technology) (in Chinese)
[11] 答嘉曦, 洪越明, 董天临 2006 2005'全国微波毫米波会议论文集 (第三册) 中国 深圳, 2月27日−3月2日, 2006 pp64−67
Da J X, Hong Y M, Dong T L 2006 2005' National Microwave and Millimeter Wave Conference Papers Collection (Vol.3) Shenzhen, China, February 27−March 2, 2006 pp64−67 (in Chinese)
[12] 答嘉曦 2006 硕士学位论文 (武汉: 华中科技大学)
Da J X 2006 M. S. Thesis (Wuhan: Huazhong University of Science and Technology) (in Chinese)
[13] 刘毅 2008 硕士学位论文 (武汉: 华中科技大学)
Liu Yi 2008 M. S. Thesis (Wuhan: Huazhong University of Science and Technology) (in Chinese)
[14] 田瑞霞, 王贤武, 金鹏 2014 强激光与粒子束 26 26105101
Google Scholar
Tian R X, Wang X W, Jin P 2014 High Power Laser and Particle Beam 26 26105101
Google Scholar
[15] 郝焕锋 2014 博士学位论文 (北京: 中国科学院大学)
Hao H F 2014 Ph.D. Dissertation (Beijing: University of Chinese Academy of Sciences) (in Chinese)
[16] 何小中, 杨国君, 龙继东 2014 核技术 37 10201
Google Scholar
He X Z, Yang G J, Long J D 2014 Nuclear Technol. 37 10201
Google Scholar
[17] Bhandari S, Lee G H, Klales A, Watanabe K, Taniguchi T, Heller E, Kim P, Westervelt R M 2016 Nano Lett. 16 1690
Google Scholar
[18] Xia W L, Wang Z, Lu Y R 2014 IEEE Trans. Nucl. Sci. 61 2345
Google Scholar
[19] 李平, 黄娴, 文玉梅 2012 61 137504
Google Scholar
Li P, Huang X, Wen YM 2012 Acta Phys. Sin. 61 137504
Google Scholar
[20] 李毅, 王秋良 2016 Opera3D工程电磁场计算及多场耦合分析 (北京: 清华大学出版社) 第3页
Li Y, Wang Q L 2016 Electromagnetic Field Calculation and Multi-field Coupling Analysis of Opera 3D Project (Beijing: Tsinghua University Press) p3
下载:
计量
- 文章访问数: 8984
- PDF下载量: 69
- 被引次数: 0
