高被引论文 (被引数据来源于全网,每月更新)
2025, 74 (1): 012801.
doi: 10.7498/aps.74.20241178
摘要 +
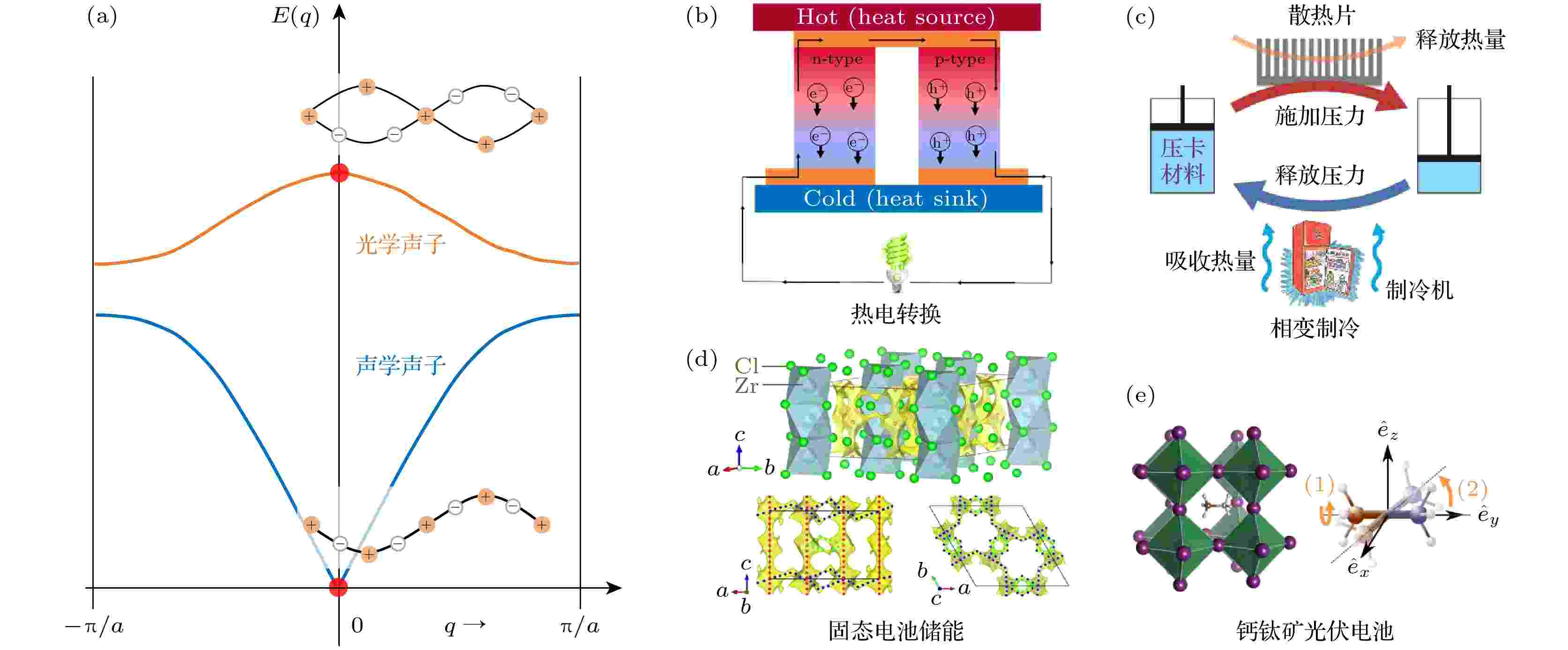
晶格动力学是众多前沿能源材料的重要物理基础. 许多优秀的能源材料具有亚晶格嵌套结构, 其晶格动力学非常复杂, 这给理解材料的物理机制带来了巨大挑战. 中子散射技术兼具高的能量和动量分辨率, 可以同时表征物质结构和复杂晶格动力学, 近年来在研究能源材料物理机制方面发挥了重要作用. 本文首先详细介绍了能源材料研究中常用的几种中子散射技术, 包括中子衍射、中子全散射、准弹性中子散射以及非弹性中子散射等. 然后, 综述了近年来以中子散射为主要表征方法在能源材料领域所取得的一些重要研究进展, 包括超离子热电材料中的超低晶格热导率、固态电解质中的离子扩散机制、压卡材料中的塑晶态相变与构型熵、光伏材料中的晶格非谐性与载流子输运以及磁卡制冷材料中的一级磁-结构相变等. 在这些能源转换与存储材料中, 晶格动力学并不是独立起作用的, 它们在宏观物理性质中的作用总是通过不同自由度如亚晶格、电荷、自旋等的复杂关联作用或相互耦合来实现的. 通过这些典型实例, 希望为能源材料与晶格动力学的进一步深入研究提供参考.
2025, 74 (2): 027702.
doi: 10.7498/aps.74.20240906
摘要 +
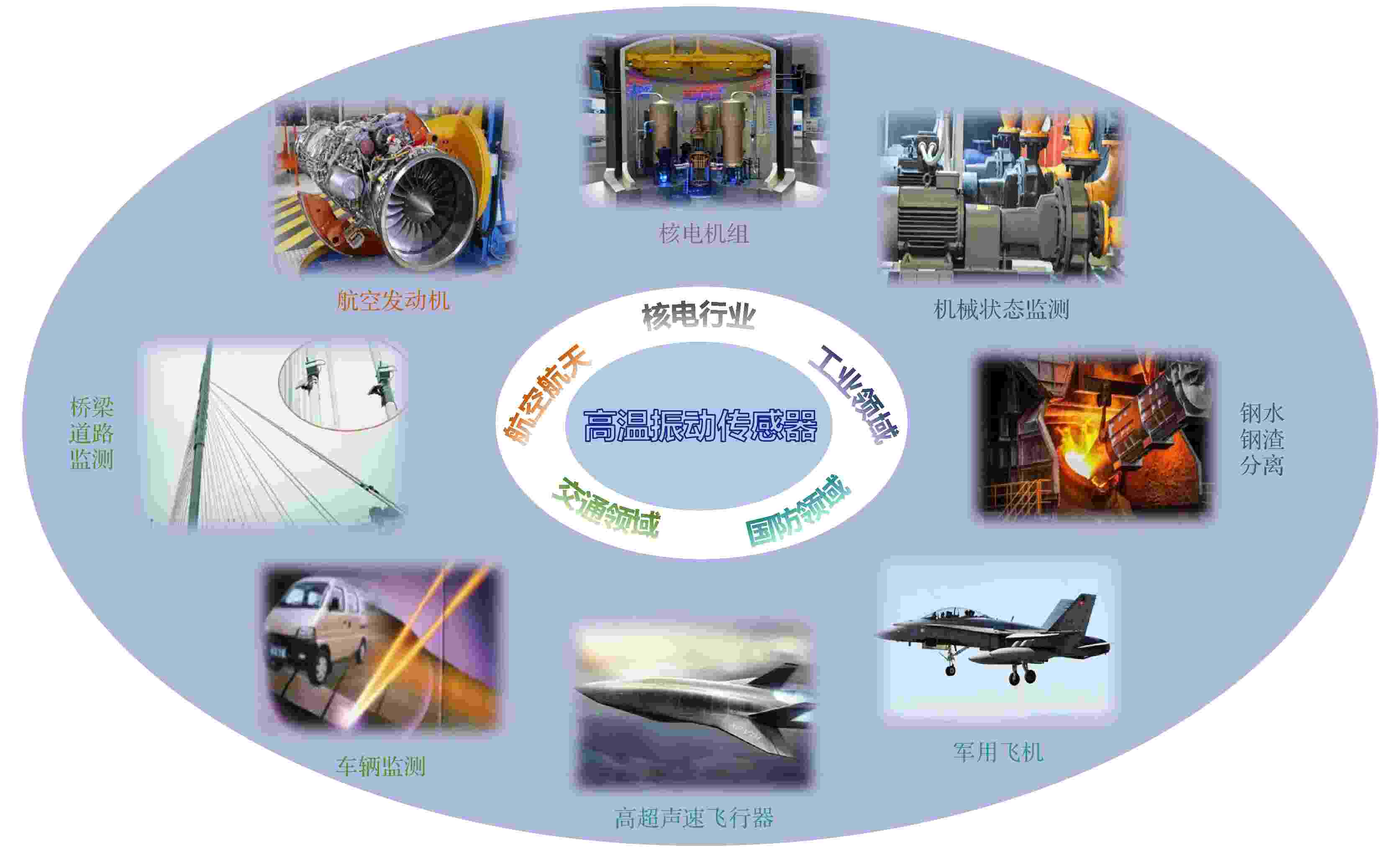
压电振动传感器与其他振动传感技术相比具有频率范围宽、动态范围大、结构简单、工作可靠、体积小等优点, 在核电行业、航空航天、轨道交通及国防军工等多个领域有着广泛的应用. 然而, 随着振动测试技术的飞速发展以及应用领域的不断拓宽, 对压电振动传感器在极端环境中长时服役的可靠性提出了更高要求, 如何提高压电振动传感器的服役温度满足极端环境下的应用需求是目前迫切解决的问题. 本文综述了高温压电传感技术应用场景和工作原理, 讨论了常见的高温压电陶瓷和晶体材料, 系统地总结了现有的压电振动传感器工作模式、不同类型压电振动传感器结构及传感器振动校准装置, 重点介绍了近年来国内外高温振动传感器的研究进展. 在此基础上, 探讨了高温压电振动传感器当前面临的问题及未来发展趋势, 为开发下一代极端环境应用的超高温振动传感器提供了思路, 有望促进国内高温压电振动传感技术的进一步研究.

2025, 74 (2): 025201.
doi: 10.7498/aps.74.20241330
摘要 +
在霍尔推力器中, 电子漂移、电子碰撞, 以及等离子体密度、温度、磁场梯度所蕴含的自由能会驱动各种频率和波长的不稳定性. 不稳定性的存在会破坏等离子体的稳定放电, 削弱推力器与电源处理单元的匹配度, 降低推力器的性能. 基于此, 本文利用基于流体模型推导的色散关系研究了霍尔推力器中由电子碰撞、等离子体密度和磁场梯度驱动的不稳定性. 结果表明: 1)在考虑电子惯性、电子与中性原子的碰撞, 以及电子${\boldsymbol{E}} \times {\boldsymbol{B}}$漂移时能够在推力器近阳极区到羽流区内的任一轴向位置处激发不稳定性. 随着角向波数${k_y}$的增大($k = 2{\text{π /}}\lambda $, $\lambda $为波长), 模式将从由碰撞激发的低杂波不稳定性转变为离子声波不稳定性. 当${k_y} = 10 {{\text{ m}}^{ - 1}}$时, 最大增长率${\gamma _{\max }}$对应频率${\omega _{\text{r}}}$随着碰撞频率${\nu _{{\text{en}}}}$的增大而轻微减小; 当$ {k_y} = 300 {{\text{ m}}^{ - 1}} $时, ${\gamma _{\max }}$对应的频率${\omega _{\text{r}}}$以及最大频率${\omega _{{\text{rmax}}}}$几乎不随碰撞频率变化. 不依赖于$ {k_y} $的大小, 对于碰撞激发的不稳定性, 模式的增长率随着碰撞频率的增大而增大. 2) 同时考虑电子惯性、电子碰撞效应, 以及密度梯度时, 密度梯度对驱动不稳定性占主导作用. 模式的动力学行为不会随${k_y}$的增大而变化, 但模式的本征值随${k_y}$的增大而增大. 在密度梯度${\kappa _{\text{N}}} = 0$的两侧, 由于密度梯度引起的抗磁性漂移频率${\omega _{\text{s}}}$的符号发生了变化, 模式的本征值在${\kappa _{\text{N}}} = 0$两侧有相反的变化趋势: 当${\omega _*}$与${\omega _{\text{r}}}$符号相反时, 密度梯度对不稳定性的激发有削弱作用(${\kappa _{\text{N}}} \gt 0$); 当${\omega _*}$与${\omega _{\text{r}}}$符号相同时, 密度梯度对不稳定性的激发有增强作用(${\kappa _{\text{N}}} \lt 0$). 3)在模型中同时考虑等离子体密度梯度、磁场梯度, 以及电子惯性和碰撞效应时, 模式本征值的变化依赖于电子的漂移频率, 以及密度和磁场梯度引起的抗磁性漂移频率的相对大小. 当仅包含密度梯度和磁场梯度时, 推力器放电通道内将出现稳定窗, 即增长率为0的区间; 包含电子惯性和碰撞效应后, 稳定窗消失.
2025, 74 (1): 012101.
doi: 10.7498/aps.74.20241201
摘要 +
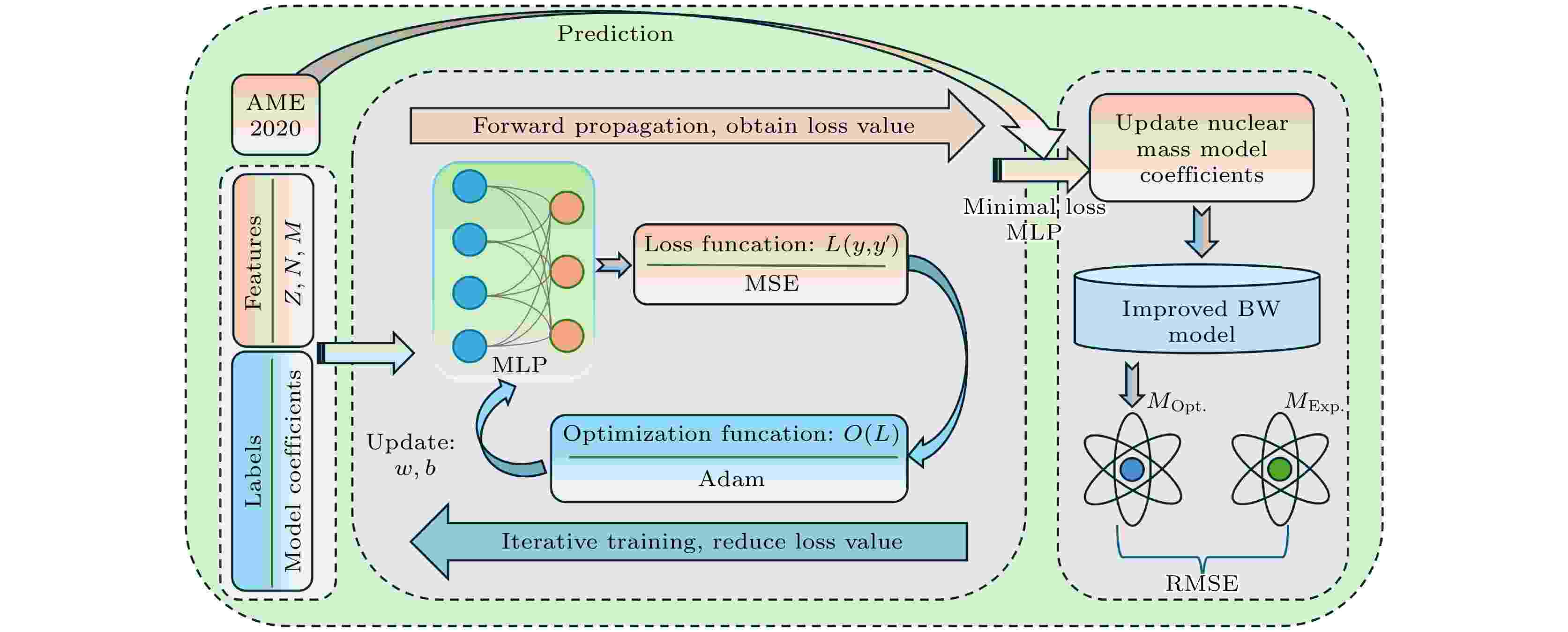
神经网络具有强大的建模能力和对大规模数据的适应性, 在拟合核质量模型参数方面表现出显著效果. 本研究旨在探索神经网络拟合核质量模型参数的问题: 采用多层感知机(multilayer perceptron, MLP)神经网络结构, 评估不同参数下Adam优化器的训练效果, 训练出准确的模型参数. 研究发现, 基于AME2020数据, 更新系数后的BW2核质量模型在双幻数以及重核区域的均方根误差降低明显; BW3模型重新拟合后的全局均方根误差为1.63 MeV, 较之前1.86 MeV有所降低. 结果表明, 该方法能够有效地拟合模型参数, 并具有良好的拟合性能和泛化能力. 这项研究为BW系列核质量模型的系数提供了新的拟合方法, 也为其他核质量寻求最佳拟合参数提供了有益的参考.
2025, 74 (1): 014202.
doi: 10.7498/aps.74.20241126
摘要 +
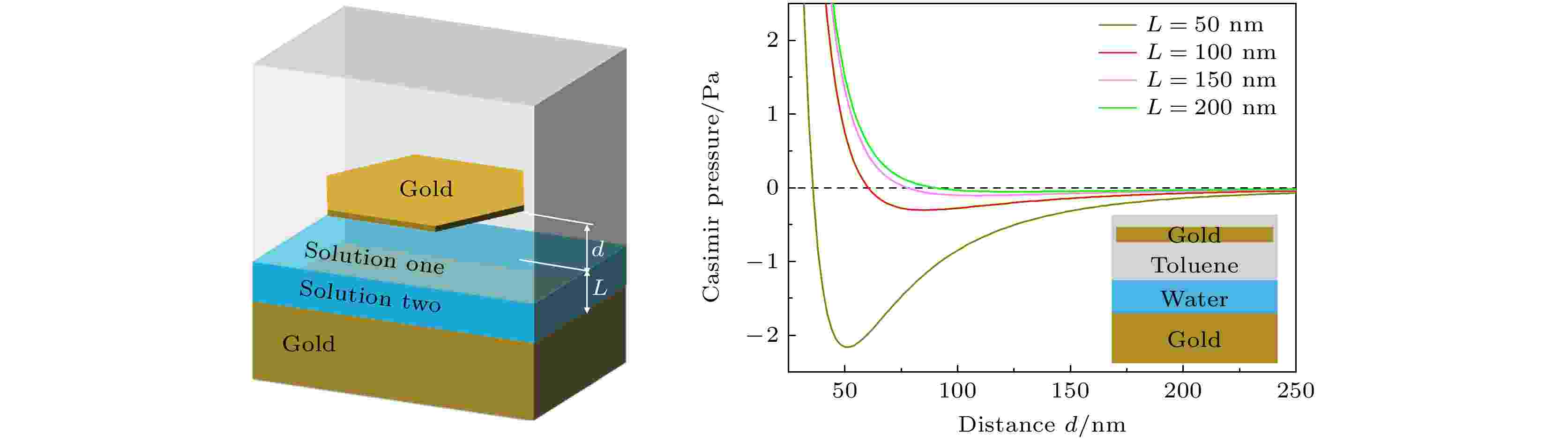
稳定的Casimir平衡点来源于Casimir能函数曲线在空间构成陷阱处的最小值. 本文提出了一种基于双液体的可调控Casimir平衡点. 在金属衬底上, 由于有机溶液和水之间的不相溶性, 形成分层液体体系. 密度低的溶液在上层, 而密度高的溶液在底层. 研究发现, 沉浸在甲苯或苯溶液中的金属悬浮薄片存在稳定的Casimir平衡点. 此外, 倒置的溴苯@水系统中也存在Casimir平衡点. 这些Casimir平衡点距离液体分层界面的高度可通过水层的厚度实现灵活调控. 最后, 还分析讨论了系统温度和水的离子浓度对Casimir平衡点的影响. 本文开辟了一种调控Casimir平衡点的新途径, 并对微纳尺度颗粒的“量子囚禁”具有重要意义.
2025, 74 (1): 017401.
doi: 10.7498/aps.74.20241534
摘要 +
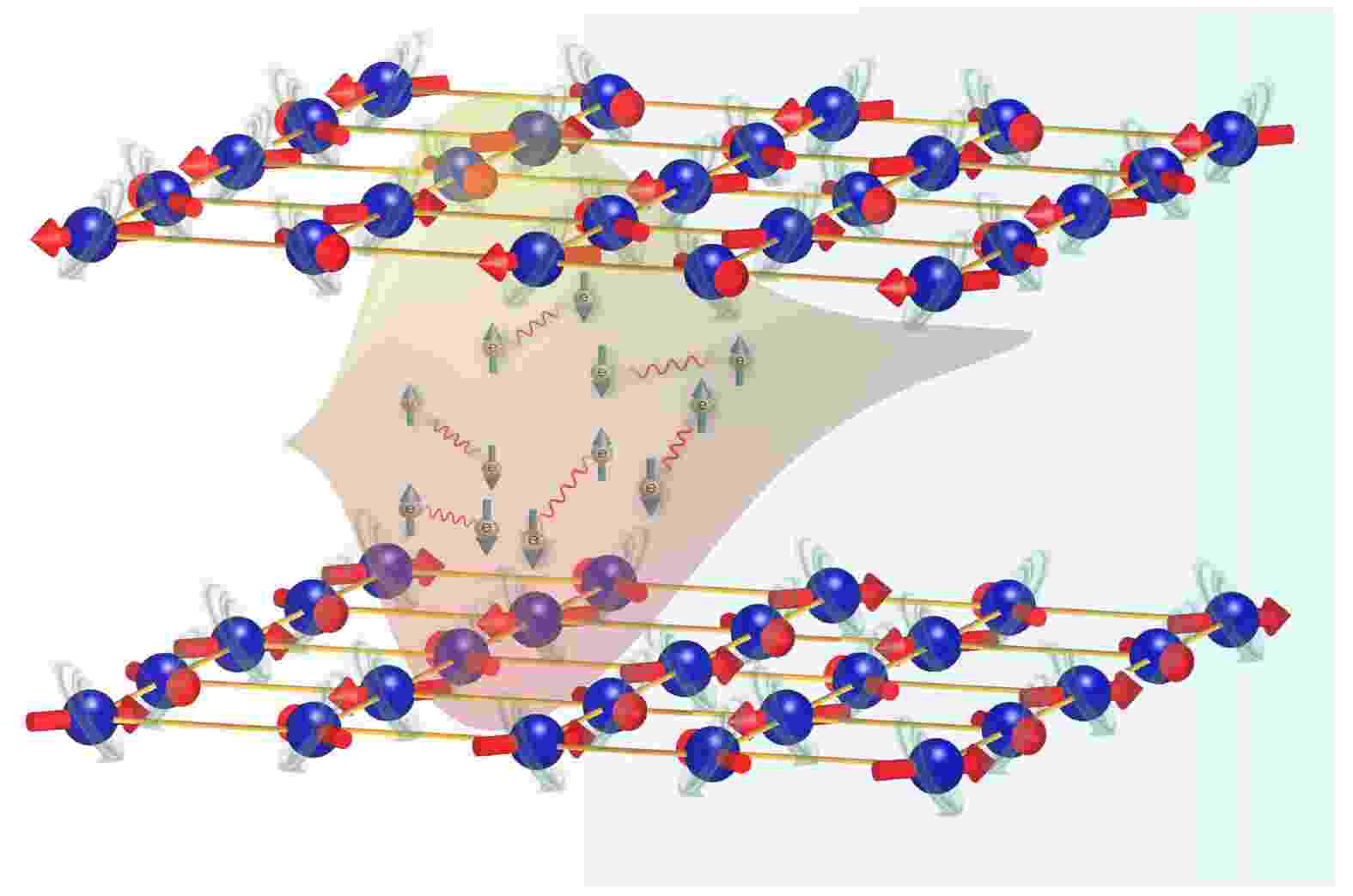
铁基超导体的多结构体系和丰富的磁性物理为理解非常规超导微观机理提供了广阔的平台, 其中自旋涨落被认为是超导配对的最可能媒介. 本文以铁砷化物超导体为例, 系统总结了铁基超导体自旋激发谱的非弹性中子散射研究结果, 并探讨了相关的普适规律; 重点介绍了铁砷化物超导体中低能自旋激发与超导电性的直接联系, 即中子自旋共振模的行为, 以及高能自旋激发谱的色散关系、强度分布、总体磁矩等特征, 并充分比较了与铜氧化物高温超导体的异同.
2025, 74 (2): 024203.
doi: 10.7498/aps.74.20241352
摘要 +
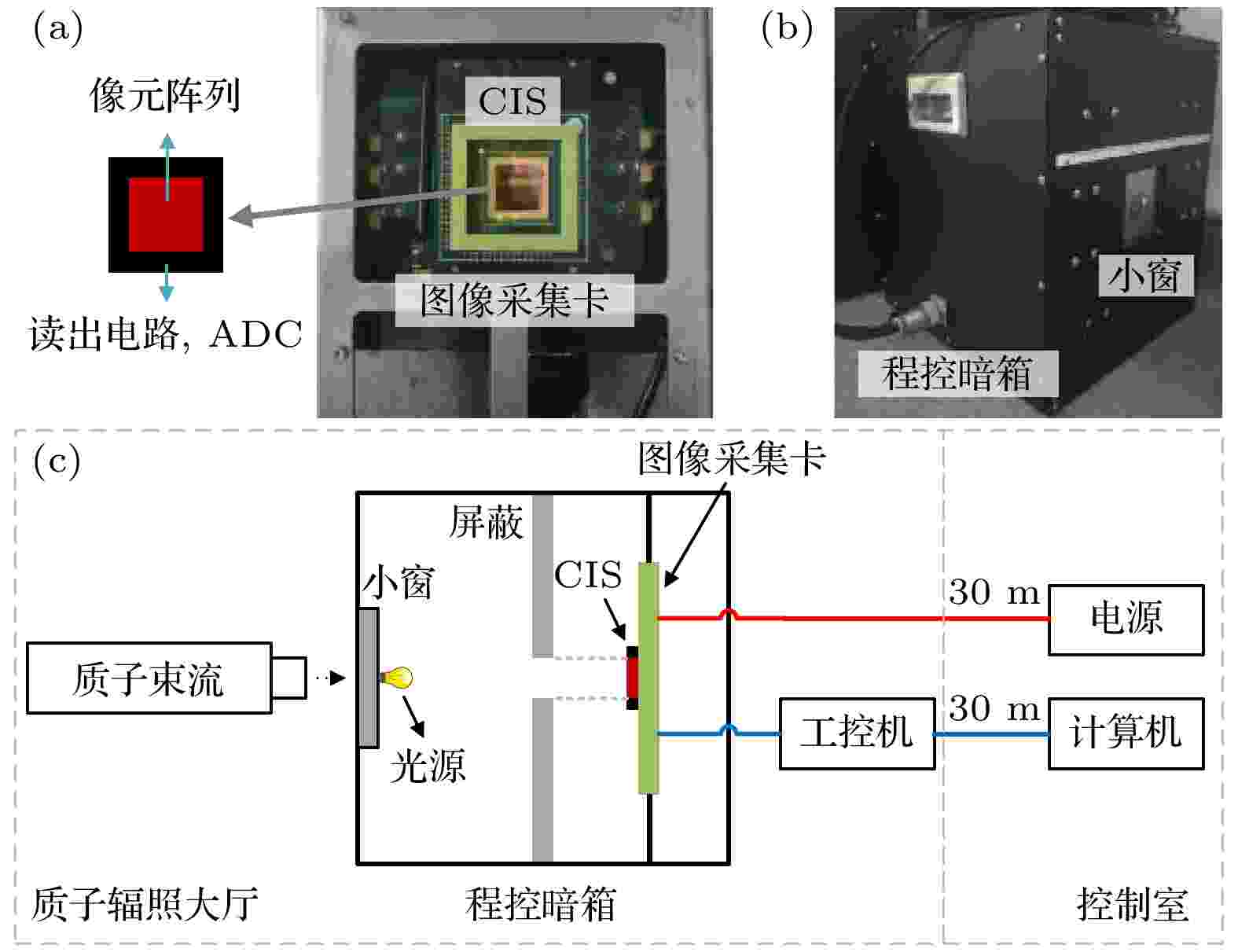
本文通过辐照实验和TCAD仿真, 研究了质子累积辐照导致四晶体管钳位光电二极管(4T PPD)CMOS图像传感器的饱和输出变化机理. 实验采用的质子能量为12 MeV和60 MeV, 最高质子注量为2×1012 cm–2. 实验结果表明: 12 MeV和60 MeV质子最高注量辐照后分别导致转换增益增大8.2%和7.3%, 满阱容量分别减小7.3%和3.8%. 饱和输出在12 MeV质子辐照下变化趋势不显著, 在60 MeV质子辐照下增大3%. 在TCAD仿真中, 建立了单个三维4T PPD像元模型, 开展了质子累积辐照效应仿真来分析损伤机理. 仿真结果表明像元饱和输出的变化由满阱容量、复位晶体管的物理特性和浮置扩散区的电容决定, 但它们具有不同的影响. 具体而言, 满阱容量的降低导致饱和输出减小, 而复位晶体管的辐照效应导致饱和输出增大. 辐照导致浮置扩散区的电容减小, 从而使转换增益增大, 进而饱和输出增大. 上述工作较为全面地揭示和分析了辐照后饱和输出的变化机理, 研究成果对CMOS图像传感器的辐射损伤分析具有一定的指导意义.
2025, 74 (6): 060701.
doi: 10.7498/aps.74.20240999
摘要 +
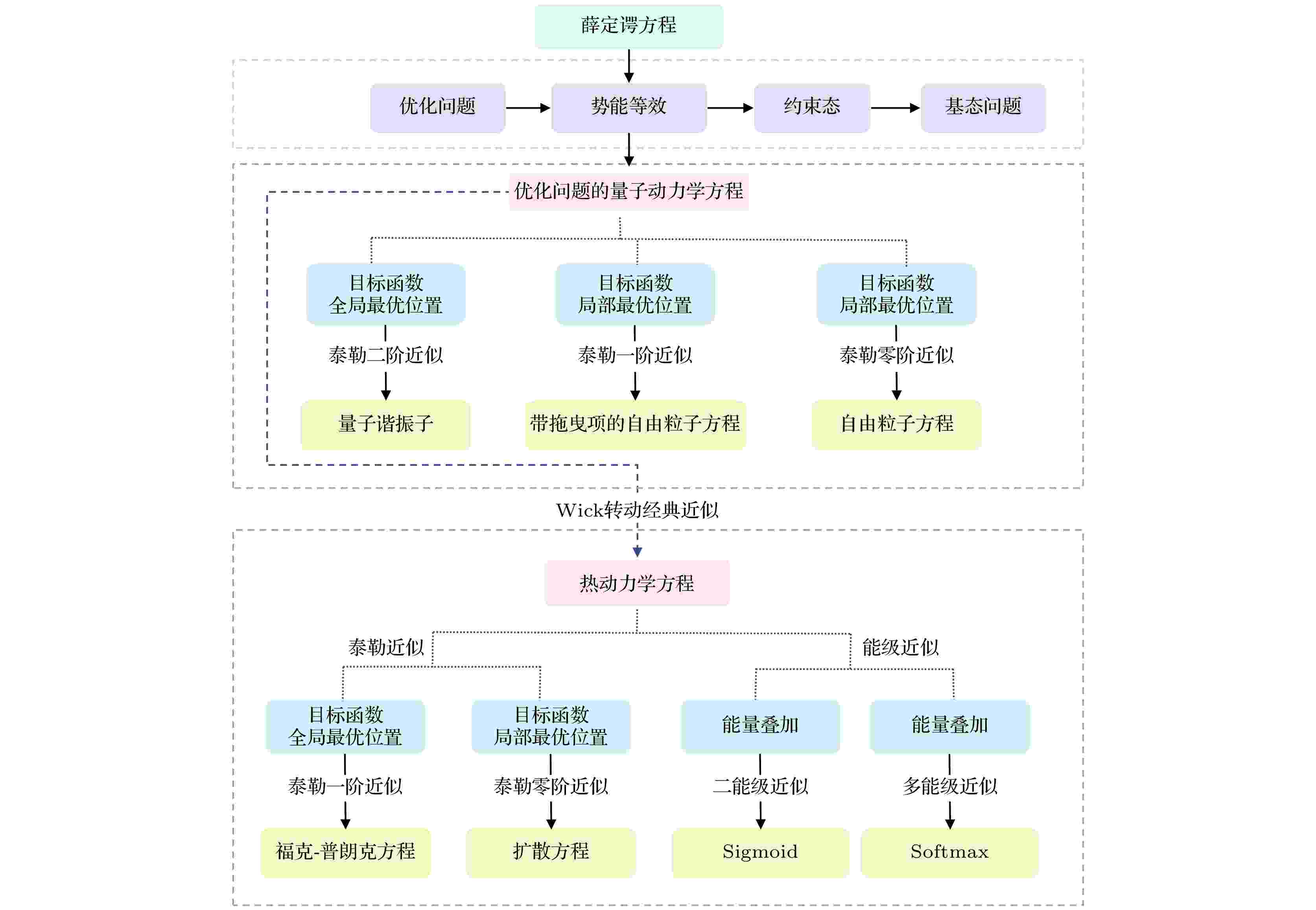
基于第一性原理思想, 采用量子动力学方法对机器学习的迭代运动过程进行建模. 在机器学习的参数空间定义广义目标函数, 利用Schrödinger方程和势能等效得到机器学习过程的量子动力学方程, 通过Wick转动进一步建立了量子动力学与热动力学的关系, 这为利用物理理论和数学理论对机器学习的迭代过程进行研究提供了可能. 本文工作将机器学习的迭代过程转化为含时偏微分方程来进行精确数学表述, 该方程表明机器学习过程可能存在多尺度的退火过程和同一尺度下的时间演化过程. 利用量子动力学方程证明了机器学习在时间演化时的收敛性, 解释了机器学习中的扩散模型是量子动力学方程在经典近似和低阶泰勒近似下的映射模型, 导出了人工智能中常用的Softmax和Sigmoid函数. 这些结果表明量子动力学方法在研究机器学习理论中是有效的.
2025, 74 (5): 057701.
doi: 10.7498/aps.74.20241379
摘要 +
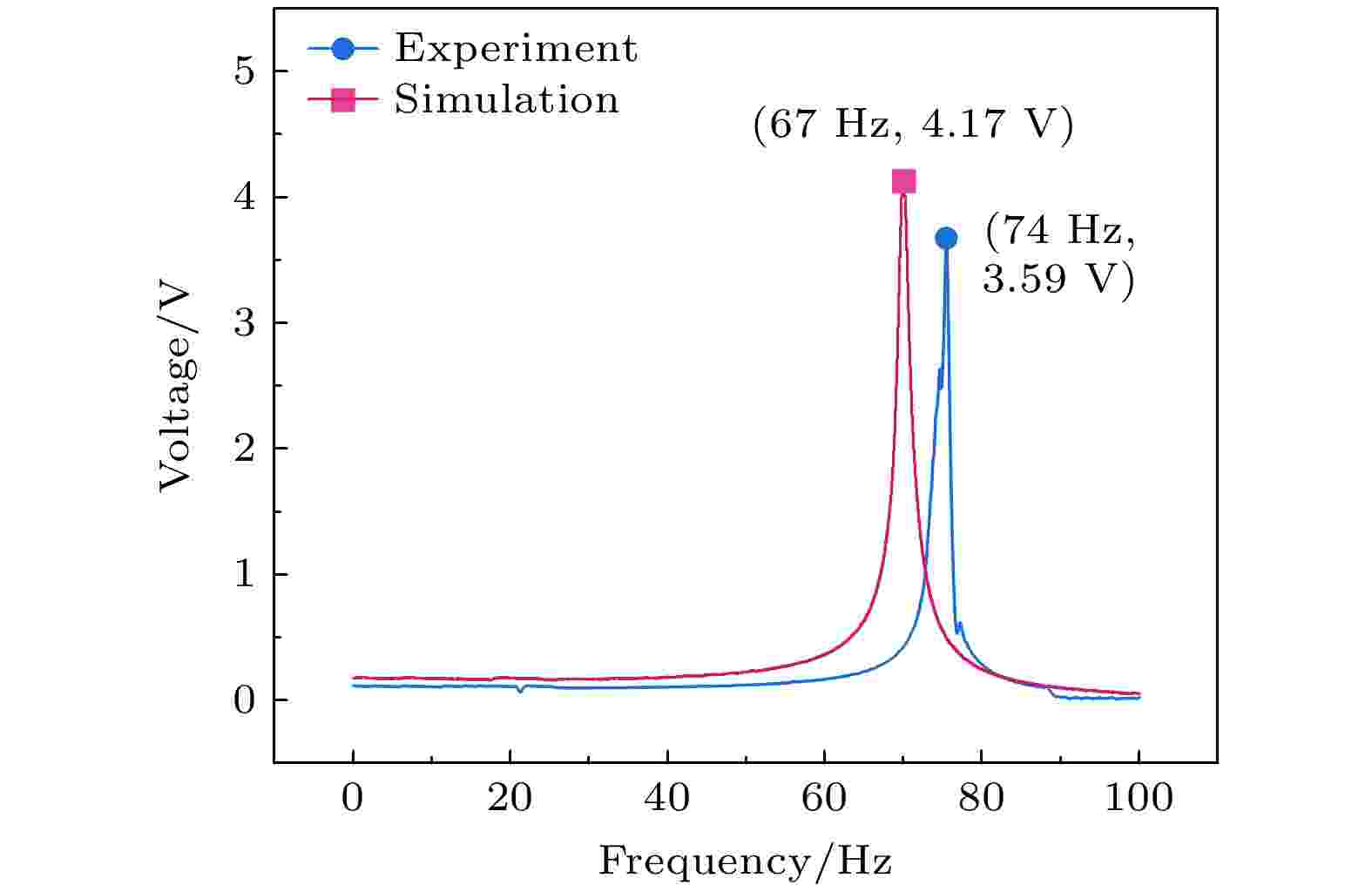
压电纤维复合材料(macro fiber composite, MFC)具有高压电性、高柔韧性和低损耗等优点, 被广泛应用于航空、航天、民用和军事等领域. 然而, 目前MFC传感器的研究主要聚焦于材料应用, 对于MFC传感器件仿真建模还缺乏系统性的研究. 本工作分别建立了代表性体积元模型、直接模型和混合模型, 从细节到整体、从微观到宏观对MFC的有限元模型进行了建模和分析. 一方面通过等效体积元模型, 掌握MFC内部的电场分布规律, 为力-电耦合提供理论依据; 另一方面通过直接模型和混合模型, 对MFC的实体结构进行整体建模和边界条件的加载, 为MFC贴片式传感和共振式传感的分析提供理论依据, 有效预测了MFC智能元件传感器的传感性能. 仿真结果表明, 共振式传感器性能远优于贴片式传感器, 当激振加速度为5 m/s2、悬臂梁基板长度为80 mm时, 计算得到的MFC共振式传感器的谐振频率为67 Hz, 输出电压为4.17 V. 实验结果表明, MFC传感器测试的谐振频率为74 Hz, 输出电压为3.59 V, 仿真计算结果与MFC传感器预测结果基本符合. 此外, MFC传感器在低频工作时具有优异的传感灵敏度, 传感灵敏度为7.35 V/g. 可见, MFC在低频共振时具有优异的传感特性, 构建的3种有限元模型可以有效预测MFC传感器的传感性能, 为MFC传感器的性能预测提供了保障.

2025, 74 (1): 014203.
doi: 10.7498/aps.74.20241458
摘要 +
分数阶涡旋光束具有分数轨道角动量(fractional orbital angular momentum, FOAM)模式, 理论上可以无限增加传输容量, 因此在光通信领域具有巨大的应用前景. 然而, 分数阶涡旋光束在自由空间传播时, 螺旋相位的不连续性使其在实际应用中容易受到衍射的影响, 进而影响FOAM阶次识别的准确度, 严重制约基于FOAM的实际应用. 如何实现有衍射条件下的分数阶涡旋光的机器学习识别, 目前仍是一个亟需解决且少见诸报道的问题. 本文提出一种基于残差网络(residual network, ResNet)的深度学习(deep learning, DL)方法, 用于精确识别分数阶涡旋光衍射过程的传播距离和拓扑荷值. 实验结果表明, 该方法可以在湍流条件下识别传播距离为100 cm, 间隔为5 cm, 模式间隔为0.1的FOAM模式, 准确率为99.69%. 该技术有助于推动FOAM模式在测距、光通信、微粒子操作等领域的实际应用.







