-
量子多体伤痕态的弱遍历性动力学与本征态热化假说相悖, 在淬火动力学中局域可观测量出现周期振荡. 这种现象通常与伤痕态二分纠缠熵的亚体积定律有关. 纠缠熵呈现出异常值, 与能谱主体相分离. 本文使用精确对角化的方法数值模拟了准一维分形子模型中的彩虹伤痕态, 该态由一系列远距离的四体纠缠组成, 依次分布于中心对称的四个格点, 其二分纠缠熵遵循体积定律. 研究发现该态在未与能谱主体分离的情况下, 表现出了弱热化现象. 当引入横场破坏模型的子系统对称性后, 弱热化特性随即消失. 进一步地, 在分形子模型中提出了彩虹伤痕态的制备方案, 通过调制局域的四体交换相互作用和$ \hat{\sigma}^z$门, 从尼尔态出发, 实现了高保真度的态制备. 分析相互作用的强度噪声影响, 该方案表现出一定的鲁棒性. 本文证明了分形子模型中彩虹伤痕态的存在, 为非平衡量子系统中弱热化的研究提供了新的途径.The eigenstate thermalization hypothesis describes the nonequilibrium dynamics of an isolated quantum many-body system, during which a pure state becomes locally indistinguishable from a thermal ensemble. The discovery of quantum many-body scars (QMBS) shows a weak violation of ergodicity, characterized by coherent oscillations of local observables after a quantum quench. These states consist of the tower of regular eigenstates which are equally spaced in the energy spectrum. Although subextensive entanglement scaling is a primary feature widely used to detect QMBS numerically as entropy outliers, rainbow scars exhibit volume-law scaling, which may challenge this property. In this work, we construct the rainbow scar state in the fracton model on a two-leg ladder. The fracton model is composed of four-body ring-exchange interactions, exhibiting global time-reversal symmetry $ \hat{{{\cal{T}}}}={{\cal{K}}} {\mathrm{i}} \hat{\sigma}^y $ and subsystem $ {\hat{U}(1)}=\displaystyle \prod\nolimits_{j \in \{\text {row/col}\}} {\mathrm{exp}}\Big({{\mathrm{i}} \dfrac{\theta}{2} \hat{\sigma}_j^z}\Big)$ symmetry. The subsystem symmetry constrains particle mobility, hindering the establishment of thermal equilibrium and leading to a series of anomalous dynamical processes. We construct the rainbow scar state with distributed four-body GHZ states whose entanglement entropy follows the volume law. By calculating the eigenstates of the fracton model with exact diagonalization, the rainbow scar state consists of a series of degenerate high-energy excited states that are not significant outliers among other eigenstates in the spectrum. By introducing the on-site interaction to break the time-reversal symmetry, the degeneracy of rainbow scar states is lifted into an equally spaced tower of states, ensuring the revival of the initial state. However, when subsystem $\hat U(1) $ symmetry is broken, the scar state is quickly thermalized, indicating that the weak thermalization may be protected by subsystem $\hat U(1) $ symmetry. Additionally, we propose a scheme for preparing the rainbow scar state by modulating the strength of the four-body interaction and $ \hat{\sigma}^z$ operations, analyzing the influence of noise on the strength of the four-body interaction. This work provides new insights into the weak thermalization processes in fracton model and aids in understanding the nature of ETH-violation in various nonequilibrium systems.
[1] Polkovnikov A, Sengupta K, Silva A, Vengalattore M 2011 Rev. Mod. Phys. 83 863
 Google Scholar
Google Scholar
[2] Dmitriev I A, Mirlin A D, Polyakov D G, Zudov M A 2012 Rev. Mod. Phys. 84 1709
 Google Scholar
Google Scholar
[3] Pekola J P, Karimi B 2021 Rev. Mod. Phys. 93 041001
 Google Scholar
Google Scholar
[4] Deutsch J M 1991 Phys. Rev. A 43 2046
 Google Scholar
Google Scholar
[5] Srednicki M 1994 Phys. Rev. E 50 888
 Google Scholar
Google Scholar
[6] Rigol M, Dunjko V, Yurovsky V, Olshanii M 2007 Phys. Rev. Lett. 98 050405
 Google Scholar
Google Scholar
[7] Calabrese P, Essler F H L, Fagotti M 2011 Phys. Rev. Lett. 106 227203
 Google Scholar
Google Scholar
[8] Nandkishore R, Huse D A 2015 Annu. Rev. Condens. Matter Phys. 6 15
 Google Scholar
Google Scholar
[9] Schreiber M, Hodgman S S, Bordia P, Lüschen H P, Fischer M H, Vosk R, Altman E, Schneider U, Bloch I 2015 Science 349 842
 Google Scholar
Google Scholar
[10] Moudgalya S, Rachel S, Bernevig B A, Regnault N 2018 Phys. Rev. B 98 235155
 Google Scholar
Google Scholar
[11] Choi S, Turner C J, Pichler H, Ho W W, Michailidis A A, Papic Z, Serbyn M, Lukin M D, Abanin D A 2019 Phys. Rev. Lett. 122 220603
 Google Scholar
Google Scholar
[12] Schecter M, Iadecola T 2019 Phys. Rev. Lett. 123 147201
 Google Scholar
Google Scholar
[13] Shiraishi N, Mori T 2017 Phys. Rev. Lett. 119 030601
 Google Scholar
Google Scholar
[14] Lin C J, Motrunich O I 2019 Phys. Rev. Lett. 122 173401
 Google Scholar
Google Scholar
[15] Ok S, Choo K, Mudry C, Castelnovo C, Chamon C, Neupert T 2019 Phys. Rev. Res. 1 033144
 Google Scholar
Google Scholar
[16] Langlett C M, Yang Z C, Wildeboer J, Gorshkov A V, Iadecola T, Xu S 2022 Phys. Rev. B 105 L060301
 Google Scholar
Google Scholar
[17] Wildeboer J, Langlett C M, Yang Z C, Gorshkov A V, Iadecola T, Xu S 2022 Phys.Rev. B 106 205142
 Google Scholar
Google Scholar
[18] Iversen M, Bardarson J H, Nielsen E B 2024 Phys. Rev. A 109 023310
 Google Scholar
Google Scholar
[19] Ramírez G, Rodríguez-Laguna J, Sierra G 2015 J. Stat. Mech.: Theory Exp. 2015 06002
 Google Scholar
Google Scholar
[20] Ramírez G, Rodríguez-Laguna J, Sierra G 2014 J. Stat. Mech. : Theory Exp. 2014 10004
 Google Scholar
Google Scholar
[21] Dutta S, Kuhr S, Cooper N R 2024 Phys. Rev. Res. 6 L012039
 Google Scholar
Google Scholar
[22] Byles L, Sierra G, Pachos J K 2024 New J. Phys. 26 013055
 Google Scholar
Google Scholar
[23] Serbyn M, Abanin D A, Papić Z 2021 Nat. Phys. 17 675
 Google Scholar
Google Scholar
[24] Moudgalya S, Bernevig B A, Regnault N 2022 Rep. Prog. Phys. 85 086501
 Google Scholar
Google Scholar
[25] Srivatsa N S, Yarloo H, Moessner R, Nielsen E B 2023 Phys.Rev. B 108 L100202
 Google Scholar
Google Scholar
[26] Haah J 2011 Phys. Rev. A 83 042330
 Google Scholar
Google Scholar
[27] Vijay S, Haah J, Fu L 2016 Phys. Rev. B 94 235157
 Google Scholar
Google Scholar
[28] Pretko M, Radzihovsky L 2018 Phys. Rev. Lett. 120 195301
 Google Scholar
Google Scholar
[29] Gromov A, Radzihovsky L 2024 Rev. Mod. Phys. 96 011001
 Google Scholar
Google Scholar
[30] Du Y H, Mehta U, Nguyen D, Son D T 2022 SciPost. Phys. 12 050
 Google Scholar
Google Scholar
[31] Prem A, Huang S J, Song H, Hermele H 2019 Phys. Rev. X 9 021010
 Google Scholar
Google Scholar
[32] Benedetti V, Bueno P, Magan J M 2023 Phys. Rev. Lett. 131 111603
 Google Scholar
Google Scholar
[33] Prem A, Haah J, Nandkishore R 2017 Phys. Rev. B 95 155133
 Google Scholar
Google Scholar
[34] Pretko M 2017 Phys. Rev. B 96 115102
 Google Scholar
Google Scholar
[35] Pai S, Pretko M 2019 Phys. Rev. Lett. 123 136401
 Google Scholar
Google Scholar
[36] Pretko M, Chen X, You Y 2020 Int. J. Mod. Phys. A 35 2030003
 Google Scholar
Google Scholar
[37] Sala P, Rakovszky T, Verresen R, Knap M, Pollmann F 2020 Phys. Rev. X 10 011047
 Google Scholar
Google Scholar
[38] Scherg S, Kohlert T, Sala P, Pollmann F, Madhusudhana H B, Bloch I, Aidelsburger M 2021 Nat. Commun. 12 4490
 Google Scholar
Google Scholar
[39] Kohlert T, Scherg S, Sala P, Pollmann F, Madhusudhana H B, Bloch I, Aidelsburger M 2023 Phys. Rev. Lett. 130 010201
 Google Scholar
Google Scholar
[40] Adler D, Wei D, Will M, Srakaew K, Agrawal S, Weckesser P, Moessner R, Pollmann F, Bloch I, Aidelsburger M 2024 Nature 636 80
 Google Scholar
Google Scholar
[41] Imai S, Tsuji N 2025 Phys. Rev. Res. 7 013064
 Google Scholar
Google Scholar
[42] Weinberg P, Bukov M 2019 SciPost Phys. 7 020
 Google Scholar
Google Scholar
[43] Aasen D, Bulmash D, Prem A, Slagle K, Williamson D J 2020 Phys. Rev. Res. 2 043165
 Google Scholar
Google Scholar
[44] You Y Z, Burnell F J, Hughes T L 2021 Phys. Rev. B 103 245128
 Google Scholar
Google Scholar
[45] Paredes B, Bloch I 2008 Phys. Rev. A 77 023603
 Google Scholar
Google Scholar
[46] Dai H N, Yang B, Reingruber A, Sun H, Xu X F, Chen Y A, Yuan Z S, Pan J W 2017 Nat. Phys 13 1195
 Google Scholar
Google Scholar
[47] Marcos D, Widmer P, Rico E, Hafezi M, Rabl P, Wiese U J, Zoller P 2014 Ann. Phys. 351 634
 Google Scholar
Google Scholar
[48] Sala P, Rakovszky T, Verresen R, Knap M, Pollmann F 2020 Phys. Rev. B 101 125126
 Google Scholar
Google Scholar
[49] Khudorozhkov A, Tiwari A, Chamon C, Neupert T 2022 SciPost Phys. 13 098
 Google Scholar
Google Scholar
[50] O'Dea N, Burnell F, Chandran A, Khemani V 2020 Phys. Rev. Res. 2 043305
 Google Scholar
Google Scholar
[51] Ren J, Liang C, Fang C 2021 Phys. Rev. Lett. 126 120604
 Google Scholar
Google Scholar
[52] Zhao H Z, Smith A, Mintert F, Knolle J 2021 Phys. Rev. Lett. 127 150601
 Google Scholar
Google Scholar
[53] Ho W W, Choi S Pichler H, Lukin M D 2019 Phys. Rev. Lett. 122 040603
 Google Scholar
Google Scholar
[54] Mondragon-Shem I, Vavilov M G, Martin I 2021 PRX Quantum 2 030349
 Google Scholar
Google Scholar
[55] Barmettler P, Rey A M, Demler E, Lukin M D, Bloch I, Gritsev V 2008 Phys. Rev. A 78 012330
 Google Scholar
Google Scholar
[56] Alkurtass B, Banchi L, Bose S 2014 Phys. Rev. A 90 042304
 Google Scholar
Google Scholar
[57] Glaser S J, Boscain U, Calarco T, Koch C P, Köckenberger W, Kosloff R, Kuprov I, Luy B, Schirmer S, Schulte-Herbrüggen T, Sugny D, Wilhelm F K 2015 Eur. Phys. J. D 69 279
 Google Scholar
Google Scholar
[58] Carleo G, Cirac I, Cranmer K, Daudet L, Schuld M, Tishby N, Vogt-Maranto L, Zdeborová L 2019 Rev. Mod. Phys. 91 045002
 Google Scholar
Google Scholar
[59] Buijsman W 2022 Phys. Rev. B 106 045104
 Google Scholar
Google Scholar
[60] Dong Y, Zhang S Y, Deng D L 2023 Phys. Rev. B 108 195133
 Google Scholar
Google Scholar
[61] Schuster T, Kobrin B, Gao P, Cong I, Khabiboulline E T, Linke N M, Lukin M D, Monroe C, Yoshida B, Yao N Y 2022 Phys. Rev. X 12 031013
 Google Scholar
Google Scholar
[62] Agarwal L, Langlett C M, Xu S 2023 Phys. Rev. Lett. 130 020801
 Google Scholar
Google Scholar
-
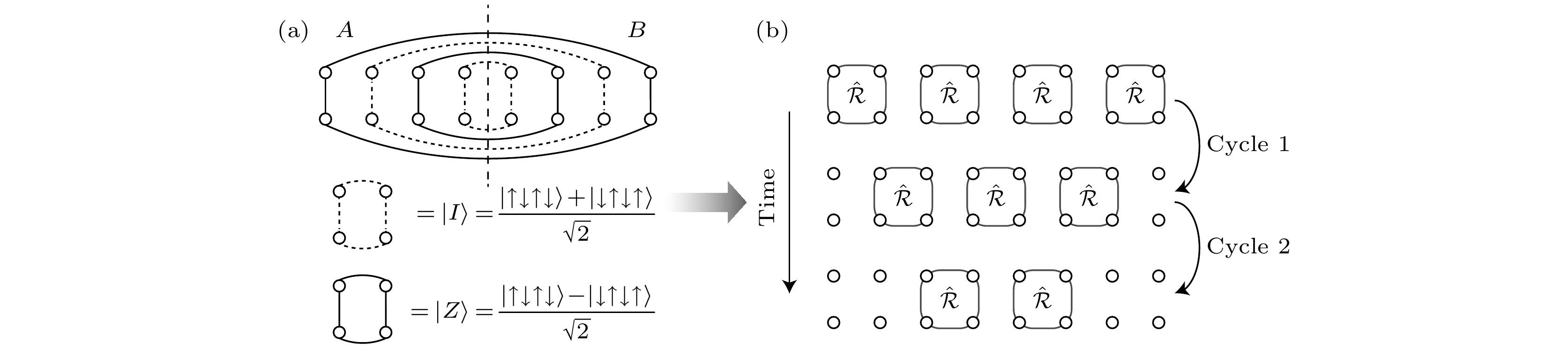
图 1 (a)分形子模型中彩虹伤痕态的示意图, 中心对称的四个格点间形成交错的四体GHZ态$ (|I\rangle $和$ |Z\rangle) $; (b)调制四体相互作用$ \hat{{\cal{R}}} $, 在晶格的两端形成四体纠缠态. 通过多周期调制和交错的$ \hat{\sigma}^z $门操作实现态制备
Fig. 1. (a) Rainbow scar state with each bond a distributed four-qubit GHZ state $|I\rangle$ and $|Z\rangle$; (b) illustration for the preparation of rainbow scar states by modulating four-body ring-exchange interactions $ \hat{{\cal{R}}} $ and gate operations $ \hat{\sigma}^z $.
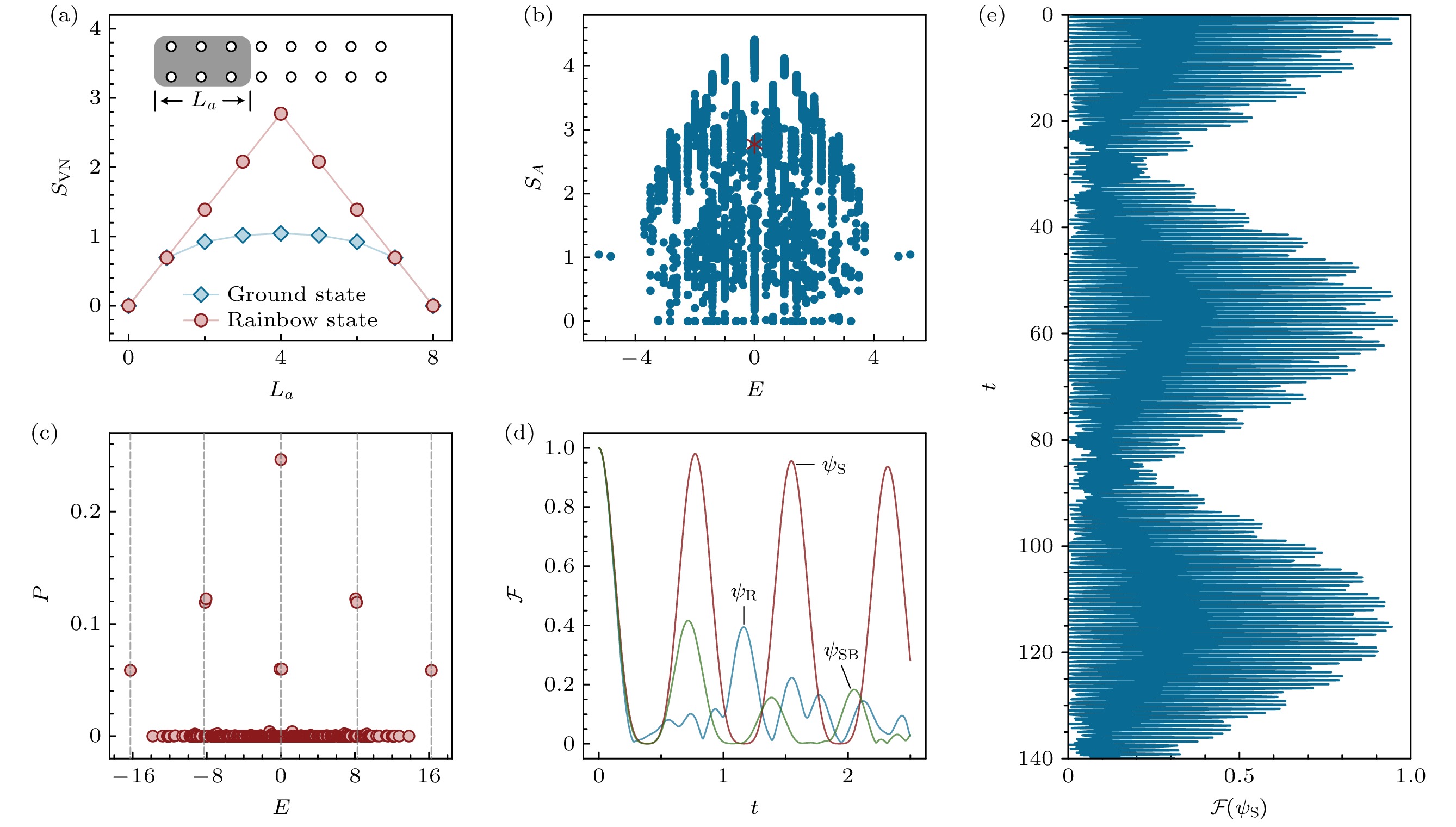
图 2 (a)分形子模型中彩虹伤痕态(红色圆形)和基态(蓝色菱形)的二分冯·诺依曼纠缠熵, 子空间a的长度为$ L_a\in [0, L]$; (b)均匀分割子空间$ L_a = L/2 $, 周期性边界条件下分形子模型的不同本征态的二分纠缠熵$ S_A $, 红色的星形代表彩虹伤痕态; (c)引入外场后, 破坏彩虹伤痕态内部对称性, 不同能量的本征态占比呈现等间隔分布; (d)外场作用下的淬火动力学$ (h_z = 2, J_i = J_{AB} = 1) $, 蓝色实线为彩虹态, 红色实线为彩虹伤痕态, 绿色实线为破坏子系统$\hat U(1) $对称性后的彩虹伤痕态; (e)外场作用下的彩虹伤痕态在大时间尺度下的周期性振荡行为. 上述结果通过精确对角化$ 2\times 8 $的梯子晶格计算得到
Fig. 2. (a) The bipartite von Neumann entanglement entropy of the rainbow scar state (red circle) and the ground state (blue diamond), with the length of subspace a being $ L_a \in [0, L] $; (b) the bipartite entanglement entropy of the eigenstates of the fracton model under periodic boundary conditions with $ L_a = L/2 $, where the red star represents the result of the rainbow scar state; (c) the overlap between the rainbow scar state and each energy eigenstate after breaking the internal symmetry of the rainbow scar state with $ h_z = 2, J_i = J_{AB} = 1 $; (d) the quench dynamics of fidelity with rainbow state (blue), rainbow scar states (red) and rainbow scar states without subsystem $\hat U(1) $ symmetry (green); (e) periodic oscillation behavior of rainbow scar states under external fields at long-time scales. The above results were obtained through exact diagonalization calculations on a $ 2\times 8 $ ladder lattice
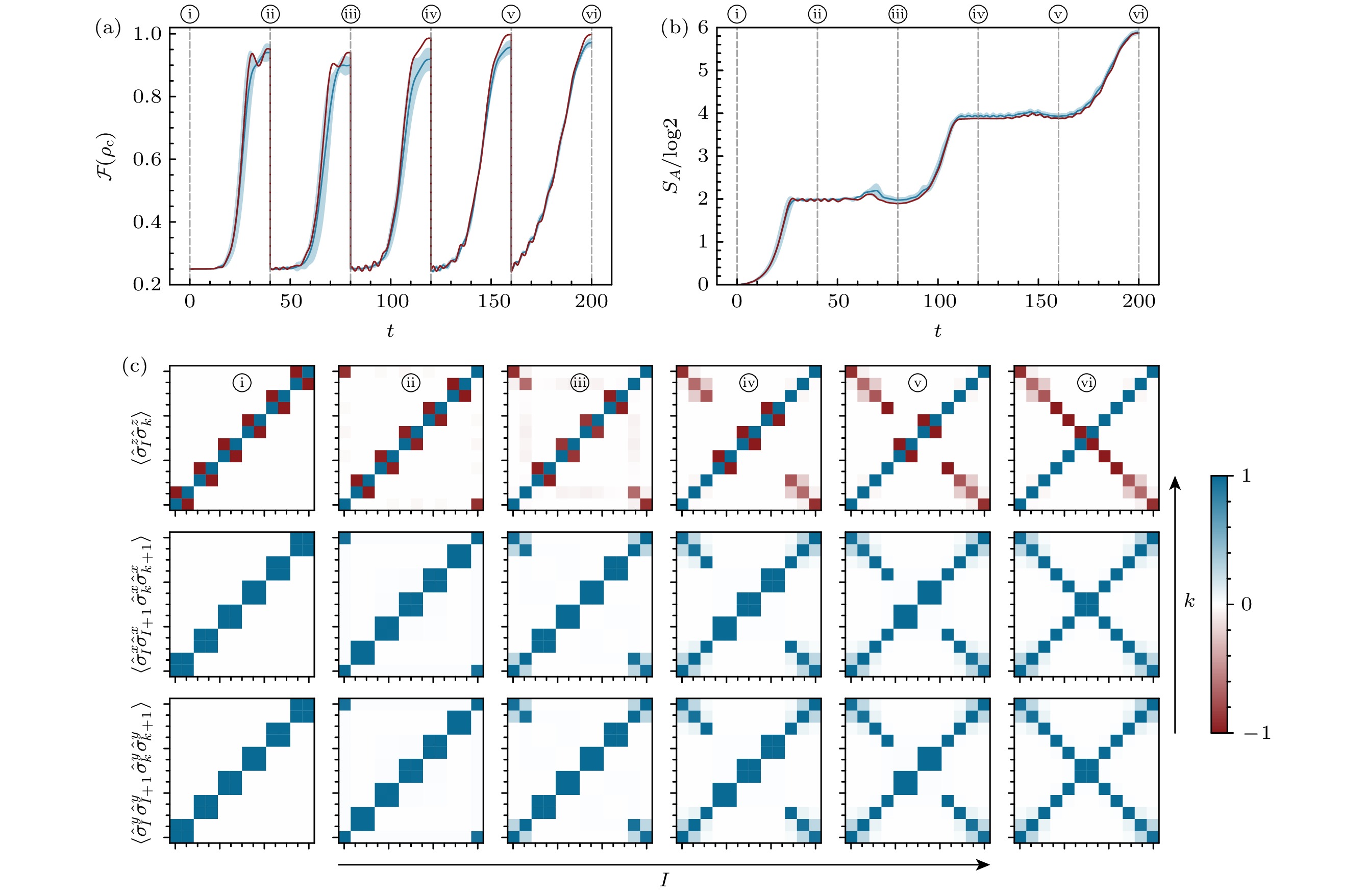
图 3 (a)通过线性调制四体相互作用的强度$ J_{{\mathrm{o(e)}}} $, 各个演化周期下, 中心对称的四个格子形成GHZ态的保真度随时间的演化. (b)均匀分割的二分纠缠熵随时间逐渐增长为$ L/2\log2 $, 红色曲线代表无噪声情况, 蓝色曲线为相互作用强度噪声$ J\sim {\cal{N}}(1, 0.2^2) $影响下三次模拟的平均, 阴影为相应的标准差. (c)中心对称格点间的自旋关联的建立过程. 系统尺寸为$ 2\times 12 $的梯子晶格
Fig. 3. (a) Time evolution of the fidelity with the distributed GHZ state through modulating the ring-exchange interaction linearly between each plaquette. (b) The von Neumann entropy $ S_A $ between two sides increases until $ L/2\log2 $. The red curve represents the noise-free case, while the blue curve represents the average of three simulations affected by Gaussian noise $ {\cal{N}}(1, 0.2^2) $, with the blue shadow indicating the corresponding standard deviation. (c) Two-site and four-site spin-spin correlations between centrosymmetric sites develop during the evolution. The geometry of the ladder is $ 2\times 12 $.
-
[1] Polkovnikov A, Sengupta K, Silva A, Vengalattore M 2011 Rev. Mod. Phys. 83 863
 Google Scholar
Google Scholar
[2] Dmitriev I A, Mirlin A D, Polyakov D G, Zudov M A 2012 Rev. Mod. Phys. 84 1709
 Google Scholar
Google Scholar
[3] Pekola J P, Karimi B 2021 Rev. Mod. Phys. 93 041001
 Google Scholar
Google Scholar
[4] Deutsch J M 1991 Phys. Rev. A 43 2046
 Google Scholar
Google Scholar
[5] Srednicki M 1994 Phys. Rev. E 50 888
 Google Scholar
Google Scholar
[6] Rigol M, Dunjko V, Yurovsky V, Olshanii M 2007 Phys. Rev. Lett. 98 050405
 Google Scholar
Google Scholar
[7] Calabrese P, Essler F H L, Fagotti M 2011 Phys. Rev. Lett. 106 227203
 Google Scholar
Google Scholar
[8] Nandkishore R, Huse D A 2015 Annu. Rev. Condens. Matter Phys. 6 15
 Google Scholar
Google Scholar
[9] Schreiber M, Hodgman S S, Bordia P, Lüschen H P, Fischer M H, Vosk R, Altman E, Schneider U, Bloch I 2015 Science 349 842
 Google Scholar
Google Scholar
[10] Moudgalya S, Rachel S, Bernevig B A, Regnault N 2018 Phys. Rev. B 98 235155
 Google Scholar
Google Scholar
[11] Choi S, Turner C J, Pichler H, Ho W W, Michailidis A A, Papic Z, Serbyn M, Lukin M D, Abanin D A 2019 Phys. Rev. Lett. 122 220603
 Google Scholar
Google Scholar
[12] Schecter M, Iadecola T 2019 Phys. Rev. Lett. 123 147201
 Google Scholar
Google Scholar
[13] Shiraishi N, Mori T 2017 Phys. Rev. Lett. 119 030601
 Google Scholar
Google Scholar
[14] Lin C J, Motrunich O I 2019 Phys. Rev. Lett. 122 173401
 Google Scholar
Google Scholar
[15] Ok S, Choo K, Mudry C, Castelnovo C, Chamon C, Neupert T 2019 Phys. Rev. Res. 1 033144
 Google Scholar
Google Scholar
[16] Langlett C M, Yang Z C, Wildeboer J, Gorshkov A V, Iadecola T, Xu S 2022 Phys. Rev. B 105 L060301
 Google Scholar
Google Scholar
[17] Wildeboer J, Langlett C M, Yang Z C, Gorshkov A V, Iadecola T, Xu S 2022 Phys.Rev. B 106 205142
 Google Scholar
Google Scholar
[18] Iversen M, Bardarson J H, Nielsen E B 2024 Phys. Rev. A 109 023310
 Google Scholar
Google Scholar
[19] Ramírez G, Rodríguez-Laguna J, Sierra G 2015 J. Stat. Mech.: Theory Exp. 2015 06002
 Google Scholar
Google Scholar
[20] Ramírez G, Rodríguez-Laguna J, Sierra G 2014 J. Stat. Mech. : Theory Exp. 2014 10004
 Google Scholar
Google Scholar
[21] Dutta S, Kuhr S, Cooper N R 2024 Phys. Rev. Res. 6 L012039
 Google Scholar
Google Scholar
[22] Byles L, Sierra G, Pachos J K 2024 New J. Phys. 26 013055
 Google Scholar
Google Scholar
[23] Serbyn M, Abanin D A, Papić Z 2021 Nat. Phys. 17 675
 Google Scholar
Google Scholar
[24] Moudgalya S, Bernevig B A, Regnault N 2022 Rep. Prog. Phys. 85 086501
 Google Scholar
Google Scholar
[25] Srivatsa N S, Yarloo H, Moessner R, Nielsen E B 2023 Phys.Rev. B 108 L100202
 Google Scholar
Google Scholar
[26] Haah J 2011 Phys. Rev. A 83 042330
 Google Scholar
Google Scholar
[27] Vijay S, Haah J, Fu L 2016 Phys. Rev. B 94 235157
 Google Scholar
Google Scholar
[28] Pretko M, Radzihovsky L 2018 Phys. Rev. Lett. 120 195301
 Google Scholar
Google Scholar
[29] Gromov A, Radzihovsky L 2024 Rev. Mod. Phys. 96 011001
 Google Scholar
Google Scholar
[30] Du Y H, Mehta U, Nguyen D, Son D T 2022 SciPost. Phys. 12 050
 Google Scholar
Google Scholar
[31] Prem A, Huang S J, Song H, Hermele H 2019 Phys. Rev. X 9 021010
 Google Scholar
Google Scholar
[32] Benedetti V, Bueno P, Magan J M 2023 Phys. Rev. Lett. 131 111603
 Google Scholar
Google Scholar
[33] Prem A, Haah J, Nandkishore R 2017 Phys. Rev. B 95 155133
 Google Scholar
Google Scholar
[34] Pretko M 2017 Phys. Rev. B 96 115102
 Google Scholar
Google Scholar
[35] Pai S, Pretko M 2019 Phys. Rev. Lett. 123 136401
 Google Scholar
Google Scholar
[36] Pretko M, Chen X, You Y 2020 Int. J. Mod. Phys. A 35 2030003
 Google Scholar
Google Scholar
[37] Sala P, Rakovszky T, Verresen R, Knap M, Pollmann F 2020 Phys. Rev. X 10 011047
 Google Scholar
Google Scholar
[38] Scherg S, Kohlert T, Sala P, Pollmann F, Madhusudhana H B, Bloch I, Aidelsburger M 2021 Nat. Commun. 12 4490
 Google Scholar
Google Scholar
[39] Kohlert T, Scherg S, Sala P, Pollmann F, Madhusudhana H B, Bloch I, Aidelsburger M 2023 Phys. Rev. Lett. 130 010201
 Google Scholar
Google Scholar
[40] Adler D, Wei D, Will M, Srakaew K, Agrawal S, Weckesser P, Moessner R, Pollmann F, Bloch I, Aidelsburger M 2024 Nature 636 80
 Google Scholar
Google Scholar
[41] Imai S, Tsuji N 2025 Phys. Rev. Res. 7 013064
 Google Scholar
Google Scholar
[42] Weinberg P, Bukov M 2019 SciPost Phys. 7 020
 Google Scholar
Google Scholar
[43] Aasen D, Bulmash D, Prem A, Slagle K, Williamson D J 2020 Phys. Rev. Res. 2 043165
 Google Scholar
Google Scholar
[44] You Y Z, Burnell F J, Hughes T L 2021 Phys. Rev. B 103 245128
 Google Scholar
Google Scholar
[45] Paredes B, Bloch I 2008 Phys. Rev. A 77 023603
 Google Scholar
Google Scholar
[46] Dai H N, Yang B, Reingruber A, Sun H, Xu X F, Chen Y A, Yuan Z S, Pan J W 2017 Nat. Phys 13 1195
 Google Scholar
Google Scholar
[47] Marcos D, Widmer P, Rico E, Hafezi M, Rabl P, Wiese U J, Zoller P 2014 Ann. Phys. 351 634
 Google Scholar
Google Scholar
[48] Sala P, Rakovszky T, Verresen R, Knap M, Pollmann F 2020 Phys. Rev. B 101 125126
 Google Scholar
Google Scholar
[49] Khudorozhkov A, Tiwari A, Chamon C, Neupert T 2022 SciPost Phys. 13 098
 Google Scholar
Google Scholar
[50] O'Dea N, Burnell F, Chandran A, Khemani V 2020 Phys. Rev. Res. 2 043305
 Google Scholar
Google Scholar
[51] Ren J, Liang C, Fang C 2021 Phys. Rev. Lett. 126 120604
 Google Scholar
Google Scholar
[52] Zhao H Z, Smith A, Mintert F, Knolle J 2021 Phys. Rev. Lett. 127 150601
 Google Scholar
Google Scholar
[53] Ho W W, Choi S Pichler H, Lukin M D 2019 Phys. Rev. Lett. 122 040603
 Google Scholar
Google Scholar
[54] Mondragon-Shem I, Vavilov M G, Martin I 2021 PRX Quantum 2 030349
 Google Scholar
Google Scholar
[55] Barmettler P, Rey A M, Demler E, Lukin M D, Bloch I, Gritsev V 2008 Phys. Rev. A 78 012330
 Google Scholar
Google Scholar
[56] Alkurtass B, Banchi L, Bose S 2014 Phys. Rev. A 90 042304
 Google Scholar
Google Scholar
[57] Glaser S J, Boscain U, Calarco T, Koch C P, Köckenberger W, Kosloff R, Kuprov I, Luy B, Schirmer S, Schulte-Herbrüggen T, Sugny D, Wilhelm F K 2015 Eur. Phys. J. D 69 279
 Google Scholar
Google Scholar
[58] Carleo G, Cirac I, Cranmer K, Daudet L, Schuld M, Tishby N, Vogt-Maranto L, Zdeborová L 2019 Rev. Mod. Phys. 91 045002
 Google Scholar
Google Scholar
[59] Buijsman W 2022 Phys. Rev. B 106 045104
 Google Scholar
Google Scholar
[60] Dong Y, Zhang S Y, Deng D L 2023 Phys. Rev. B 108 195133
 Google Scholar
Google Scholar
[61] Schuster T, Kobrin B, Gao P, Cong I, Khabiboulline E T, Linke N M, Lukin M D, Monroe C, Yoshida B, Yao N Y 2022 Phys. Rev. X 12 031013
 Google Scholar
Google Scholar
[62] Agarwal L, Langlett C M, Xu S 2023 Phys. Rev. Lett. 130 020801
 Google Scholar
Google Scholar
计量
- 文章访问数: 1453
- PDF下载量: 139
- 被引次数: 0













 下载:
下载: