剪切形变下磷烯的力学和热学性能

李婷; 毕晓月; 孔婧文

doi:10.7498/aps.72.20230084

摘要

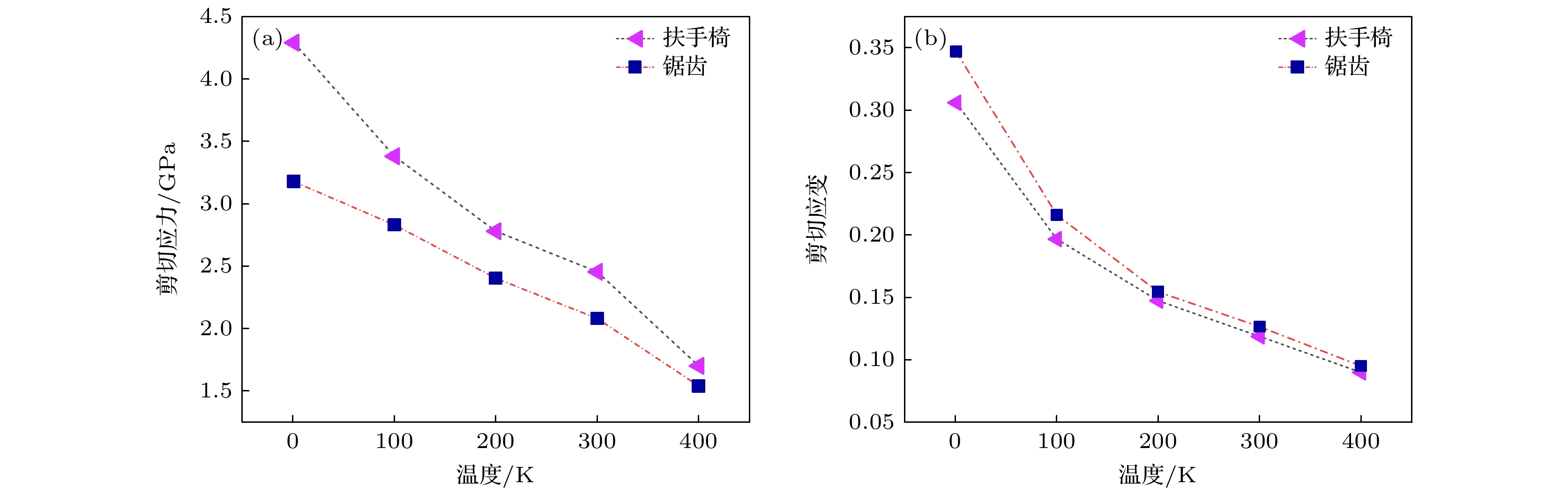
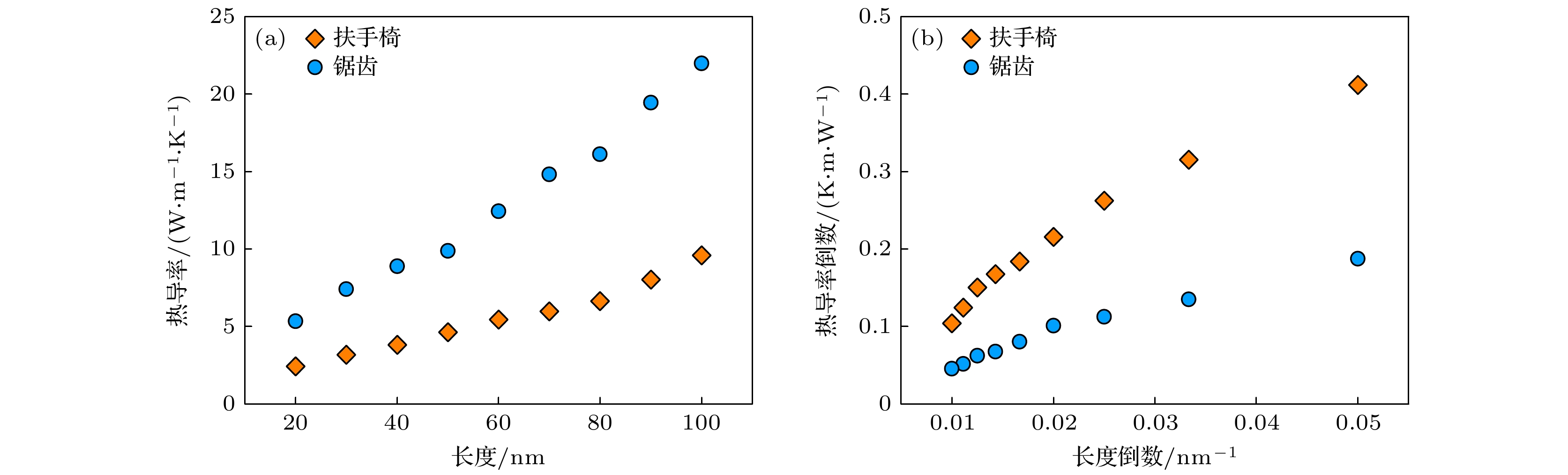
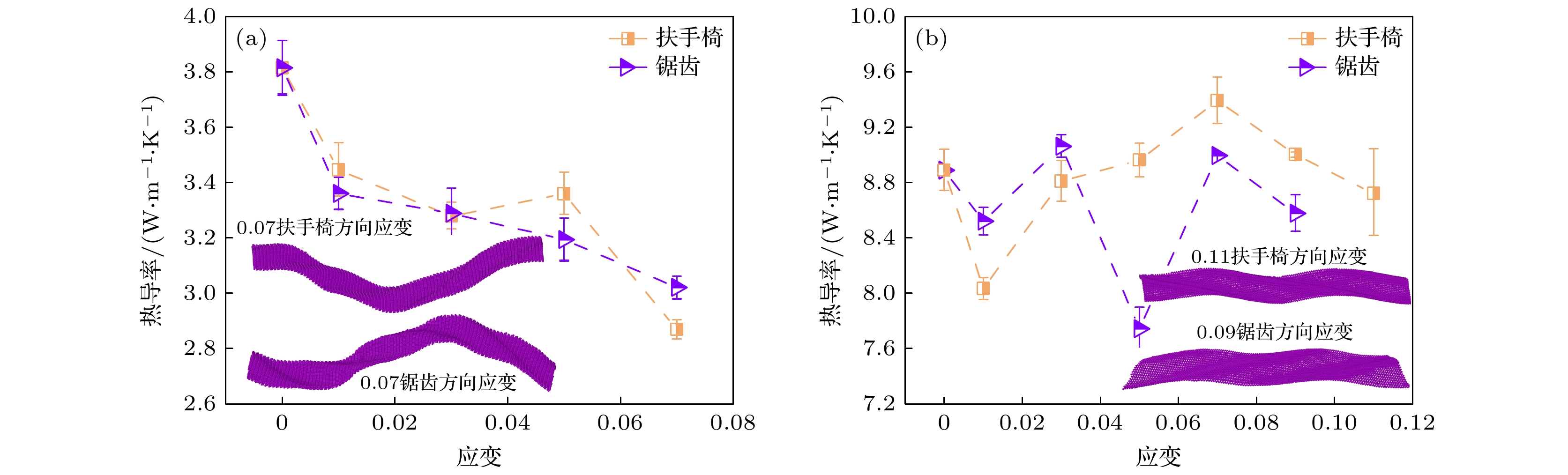
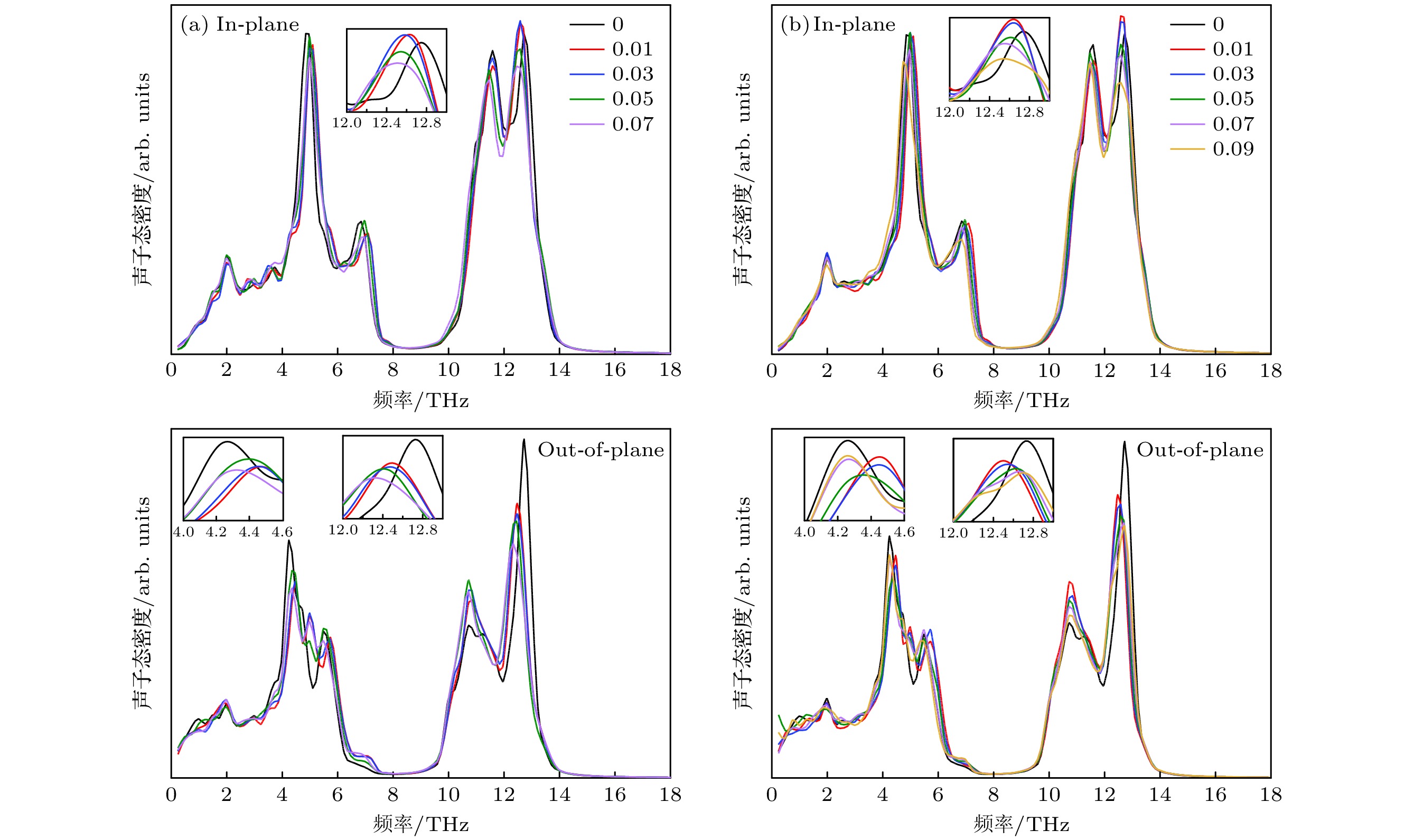
磷烯是一种新型的二维半导体材料, 近年来得到了研究者们的广泛关注. 通过分子动力学模拟对磷烯在剪切形变下的力学和热学性能进行了系统探究. 磷烯的剪切力学呈现出各向同性的特点, 沿扶手椅与锯齿方向的剪切模量均约为22 GPa. 磷烯的断裂强度和极限应变对温度十分敏感, 高温会显著削弱磷烯抗剪切形变的能力. 无应变时磷烯沿锯齿与扶手椅方向热导率的各向异性比为2.83. 当对磷烯施加剪切应变时, 磷烯沿扶手椅方向的热导率随着剪切应变的增大而减小, 但是剪切应变对磷烯锯齿方向热导率的影响则相对较弱. 通过对磷烯的声子态密度分析发现, 剪切形变主要对其柔性声子模式的振动特性具有显著影响, 使高频声子发生了红移. 同时, 剪切形变的存在会严重改变晶格的非简谐振动, 继而在不同程度上对磷烯声子间的散射产生重要的影响. 磷烯声子态密度的改变以及声子散射通道的变化共同决定了其在剪切形变下的导热特性.

关键词:

Abstract

Phosphorene, a new two-dimensional material beyond graphene, has received increasing attention in recent years owing to its superior physical properties of significant utility. Herein we carry out molecular dynamics simulations to systematically study the mechanical and thermal properties of phosphorene under shear loadings. It is found that the shear modulus of phosphorene is about 22 GPa in both the armchair direction and zigzag direction. The fracture strength and ultimate strain of phosphorene can be significantly reduced owing to stronger thermal vibrations of atoms at a higher temperature. The thermal conductivity of pristine phosphorene at room temperature is obtained, specifically, it is 18.57 W·m^–1·K^–1 along the armchair direction and 52.52 W·m^–1·K^–1 in the zigzag direction. When either an armchair- or a zigzag-oriented shear strain is applied, the armchair-oriented thermal conductivity decreases monotonically with the strain increasing. Whereas the zigzag-oriented thermal conductivity exhibits a non-monotonic behavior. The strain-induced redshift occurs in the high-frequency phonons of out-of-plane flexural modes in the phonon density of states of the sheared phosphorene. In addition, the buckled structure of phosphorene will lead the deformation characteristics under the shear strain differ from those of the planar structure such as graphene, which has a significant influence on the lattice anharmonicity and phonon scattering. It is believed that the interplay between the shift of phonon density of states and the change of phonon scattering channels results in the unique thermal transport behavior of phosphorene under shear deformation. The findings provide an insight into the understanding of the mechanical and thermal properties of phosphorene, and have significance for the future applications in phosphorene-based novel devices.

Keywords:

作者及机构信息

辽宁师范大学物理与电子技术学院, 大连　116029

通信作者: 李婷, tingli430@lnnu.edu.cn

基金项目: 辽宁省科技厅博士启动基金(批准号: 2021-BS-200)、大连市科技创新基金(批准号: 2022JJ12GX023)和辽宁师范大学2022年高端科研成果培育资助计划(批准号: 22GDL002)资助的课题.

Authors and contacts

School of Physics and Electronic Technology, Liaoning Normal University, Dalian 116029, China

Corresponding author: Li Ting, tingli430@lnnu.edu.cn

Funds: Project supported by the Science Foundation for Doctoral Research of the Department of Science and Technology of Liaoning Province, China (Grant No. 2021-BS-200), the Dalian Technological Innovation Fund Project, China (Grant No. 2022JJ12GX023), and the Liaoning Normal University 2022 Outstanding Research Achievements Cultivation Fund, China (Grant No. 22GDL002).

文章全文 : translate this paragraph

参考文献

[1]	Geim A K 2009 Science 324 1530 Google Scholar
[2]	Xu M, Liang T, Shi M, Chen H 2013 Chem. Rev. 113 3766 Google Scholar
[3]	Cai Z, Liu B, Zou X, Cheng H M 2018 Chem. Rev. 118 6091 Google Scholar
[4]	Lin Y, Connellb J W 2012 Nanoscale 4 6908 Google Scholar
[5]	Manzeli S, Ovchinnikov D, Pasquier D, Yazyev O V, Kis A 2017 Nat. Rev. Mater. 2 17033 Google Scholar
[6]	Balendhran S, Walia S, Nili H, Sriram S, Bhaskaran M 2015 Small 11 640 Google Scholar
[7]	Carvalho A, Wang M, Zhu X, Rodin A S, Su H, Neto A H C 2016 Nat. Rev. Mater. 1 16061 Google Scholar
[8]	Batmunkh M, Bat-Erdene M, Shapter J G 2016 Adv. Mater. 28 8586 Google Scholar
[9]	Akinwande D, Petrone N, Hone J 2014 Nat. Commun. 5 5678 Google Scholar
[10]	Novoselov K S, Mishchenko A, Carvalho A, Neto A H C 2016 Science 353 aac9439 Google Scholar
[11]	Bonaccorso F, Colombo L, Yu G, Stoller M, Tozzini V, Ferrari A C, Ruoff R S, Pellegrini V 2015 Science 347 1246501 Google Scholar
[12]	Jia P Z, Xie Z X, Deng Y X, Zhang Y, Tang L M, Zhou W X, Chen K Q 2022 Appl. Phys. Lett. 121 043901 Google Scholar
[13]	Zhou W X, Cheng Y, Chen K Q, Xie G, Wang T, Zhang G 2020 Adv. Funct. Mater. 30 1903829 Google Scholar
[14]	Liu H, Neal A T, Zhu Z, Luo Z, Xu X, Tománek D, Ye P D 2014 ACS Nano 8 4033 Google Scholar
[15]	Khandelwal A, Mani K, Karigerasi M H, Lahiri I 2017 Mater. Sci. Eng. B 221 17 Google Scholar
[16]	Li L, Yu Y, Ye G J, Ge Q, Ou X, Wu H, Feng D, Chen X H, Zhang Y 2014 Nat. Nanotech. 9 372 Google Scholar
[17]	Fei R, Faghaninia A, Soklaski R, Yan J A, Lo C, Yang L 2014 Nano Lett. 14 6393 Google Scholar
[18]	Qiao J, Kong X, Hu Z X, Yang F, Ji W 2014 Nat. Commun. 5 4475 Google Scholar
[19]	Tran V, Soklaski R, Liang Y, Yang L 2014 Phys. Rev. B 89 235319 Google Scholar
[20]	Jiang J W, Park H S 2014 J. Phys. D:Appl. Phys. 47 385304 Google Scholar
[21]	Sha Z D, Pei Q X, Ding Z, Jiang J W, Zhang Y W 2015 J. Phys. D: Appl. Phys. 48 395303 Google Scholar
[22]	Sha Z D, Pei Q X, Zhang Y Y, Zhang Y W 2016 Nanotech. 27 315704 Google Scholar
[23]	Li L, Yang J 2017 Nanotech. 28 475701 Google Scholar
[24]	Qin G, Hu M 2018 Small 14 1702465 Google Scholar
[25]	Hong Y, Zhang J, Zeng X C 2018 Chin. Phys. B 27 036501 Google Scholar
[26]	Qin G, Yan Q B, Qin Z, Yue S Y, Hu M, Su G 2015 Phys. Chem. Chem. Phys. 17 4854 Google Scholar
[27]	Hong Y, Zhang J, Huang X, Zeng X C 2015 Nanoscale 7 18716 Google Scholar
[28]	Ong Z Y, Cai Y, Zhang G, Zhang Y W 2014 J. Phys. Chem. C 118 25272 Google Scholar
[29]	Zhang Y Y, Pei Q X, Jiang J W, Wei N, Zhang Y W 2016 Nanoscale 8 483 Google Scholar
[30]	Liu B, Bai L, Korznikova E A, Dmitriev S V, Law A W K, Zhou K 2017 J. Phys. Chem. C 121 13876 Google Scholar
[31]	Wei Q, Peng X 2014 Appl. Phys. Lett. 104 251915 Google Scholar
[32]	Yang Z, Zhao J, Wei N 2015 Appl. Phys. Lett. 107 023107 Google Scholar
[33]	Gamil M, Zeng Q H, Zhang Y Y 2020 Phys. Lett. A 384 126784 Google Scholar
[34]	Hatam-Lee S M, Peer-Mohammadi H, Rajabpour A 2021 Mater. Today Commun. 26 101796 Google Scholar
[35]	Mahnama M, Meshkinghalam M, Ozmaian M 2022 J. Phys.: Condens. Matter 34 075403 Google Scholar
[36]	Li T 2021 Physica E 131 114761 Google Scholar
[37]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[38]	Jiang J W 2015 Nanotech. 26 315706 Google Scholar
[39]	Kheirkhah A H, Iranizad E S, Raeisi M, Rajabpour A 2014 Solid State Commun. 177 98 Google Scholar
[40]	Zhang C, Hao X L, Wang C X, Wei N, Rabczuk T 2017 Sci. Rep. 7 41398 Google Scholar
[41]	Zhao J, Jiang J W, Rabczuk T 2013 Appl. Phys. Lett. 103 231913 Google Scholar
[42]	Li T, Tang Z, Huang Z, Yu J 2017 Physica E 85 137 Google Scholar
[43]	Xu K, Fan Z, Zhang J, Wei N, Ala-Nissila T 2018 Modell. Simul. Mater. Sci. Eng. 26 085001 Google Scholar
[44]	Smith B, Vermeersch B, Carrete J, Ou E, Kim J, Mingo N, Akinwande D, Shi L 2017 Adv. Mater. 29 1603756 Google Scholar
[45]	Hu M, Zhang X, Poulikakos D 2013 Phys. Rev. B 87 195417 Google Scholar

施引文献

图 1 磷烯的原子结构　(a) 侧视图; (b) 俯视图

Fig. 1. Atomic configuration of phosphorene: (a) Side view; (b) top view.

下载: 全尺寸图片幻灯片

图 2 不同温度下磷烯的剪切应力-应变曲线　(a)扶手椅方向; (b)锯齿方向

Fig. 2. Stress-strain curves of phosphorene at different temperatures for shear deformation: (a) Armchair direction; (b) zigzag direction

下载: 全尺寸图片幻灯片

图 3 不同温度下磷烯的剪切性能　(a)断裂强度随温度的变化; (b) 极限应变随温度的变化

Fig. 3. Shear properties of phosphorene at different temperatures: (a) Fracture strength versus temperature; (b) ultimate strain versus temperature.

下载: 全尺寸图片幻灯片

图 4 磷烯沿扶手椅和锯齿方向上的热导率　(a) 热导率随长度的变化; (b) 热导率倒数与长度倒数之间的关系

Fig. 4. Thermal conductivities of phosphorene in the armchair or zigzag directions: (a) Thermal conductivities versus length; (b) inverse of thermal conductivities as a function of inverse of length.

下载: 全尺寸图片幻灯片

图 5 (a) 磷烯沿扶手椅方向的热导率与剪切应变的关系; (b) 磷烯沿锯齿方向的热导率与剪切应变的关系

Fig. 5. Thermal conductivities of phosphorene in the (a) armchair and (b) zigzag directions under shear strain.

下载: 全尺寸图片幻灯片

图 6 剪切形变下磷烯的面内(上图)与面外(下图)声子态密度　(a) 扶手椅方向; (b)锯齿方向

Fig. 6. In-plane (upper panel) and out-of-plane (lower panel) phonon density of states of phosphorene under shear deformation: (a) Armchair direction; (b) zigzag direction.

下载: 全尺寸图片幻灯片

表 1 磷烯的剪切力学性能

Table 1. Mechanical properties of phosphorene under shear loading.

文献	剪切模量/GPa	断裂强度/GPa	极限应变	计算方法
Wei和Peng^[31]	41	—	—	第一性原理
Yang等^[32]	22.1^a, 19.8^z	1.7^a, 1.4^z	0.14^a, 0.14^z	分子动力学
Gamil等^[33]	22.4^a	1.6^a	0.138^a	分子动力学
Hatam-Lee等^[34]	33.9^a, 32.5^z	2.5^a, 2.3^z	0.127^a, 0.118^z	分子动力学
本文	22.20^a, 22.34^z	2.45^a, 2.08^z	0.119^a, 0.126^z	分子动力学
注: 上标a代表扶手椅方向的结果, 上标z代表锯齿方向的结果.

下载: 导出CSV

map

[1]	Geim A K 2009 Science 324 1530 Google Scholar
[2]	Xu M, Liang T, Shi M, Chen H 2013 Chem. Rev. 113 3766 Google Scholar
[3]	Cai Z, Liu B, Zou X, Cheng H M 2018 Chem. Rev. 118 6091 Google Scholar
[4]	Lin Y, Connellb J W 2012 Nanoscale 4 6908 Google Scholar
[5]	Manzeli S, Ovchinnikov D, Pasquier D, Yazyev O V, Kis A 2017 Nat. Rev. Mater. 2 17033 Google Scholar
[6]	Balendhran S, Walia S, Nili H, Sriram S, Bhaskaran M 2015 Small 11 640 Google Scholar
[7]	Carvalho A, Wang M, Zhu X, Rodin A S, Su H, Neto A H C 2016 Nat. Rev. Mater. 1 16061 Google Scholar
[8]	Batmunkh M, Bat-Erdene M, Shapter J G 2016 Adv. Mater. 28 8586 Google Scholar
[9]	Akinwande D, Petrone N, Hone J 2014 Nat. Commun. 5 5678 Google Scholar
[10]	Novoselov K S, Mishchenko A, Carvalho A, Neto A H C 2016 Science 353 aac9439 Google Scholar
[11]	Bonaccorso F, Colombo L, Yu G, Stoller M, Tozzini V, Ferrari A C, Ruoff R S, Pellegrini V 2015 Science 347 1246501 Google Scholar
[12]	Jia P Z, Xie Z X, Deng Y X, Zhang Y, Tang L M, Zhou W X, Chen K Q 2022 Appl. Phys. Lett. 121 043901 Google Scholar
[13]	Zhou W X, Cheng Y, Chen K Q, Xie G, Wang T, Zhang G 2020 Adv. Funct. Mater. 30 1903829 Google Scholar
[14]	Liu H, Neal A T, Zhu Z, Luo Z, Xu X, Tománek D, Ye P D 2014 ACS Nano 8 4033 Google Scholar
[15]	Khandelwal A, Mani K, Karigerasi M H, Lahiri I 2017 Mater. Sci. Eng. B 221 17 Google Scholar
[16]	Li L, Yu Y, Ye G J, Ge Q, Ou X, Wu H, Feng D, Chen X H, Zhang Y 2014 Nat. Nanotech. 9 372 Google Scholar
[17]	Fei R, Faghaninia A, Soklaski R, Yan J A, Lo C, Yang L 2014 Nano Lett. 14 6393 Google Scholar
[18]	Qiao J, Kong X, Hu Z X, Yang F, Ji W 2014 Nat. Commun. 5 4475 Google Scholar
[19]	Tran V, Soklaski R, Liang Y, Yang L 2014 Phys. Rev. B 89 235319 Google Scholar
[20]	Jiang J W, Park H S 2014 J. Phys. D:Appl. Phys. 47 385304 Google Scholar
[21]	Sha Z D, Pei Q X, Ding Z, Jiang J W, Zhang Y W 2015 J. Phys. D: Appl. Phys. 48 395303 Google Scholar
[22]	Sha Z D, Pei Q X, Zhang Y Y, Zhang Y W 2016 Nanotech. 27 315704 Google Scholar
[23]	Li L, Yang J 2017 Nanotech. 28 475701 Google Scholar
[24]	Qin G, Hu M 2018 Small 14 1702465 Google Scholar
[25]	Hong Y, Zhang J, Zeng X C 2018 Chin. Phys. B 27 036501 Google Scholar
[26]	Qin G, Yan Q B, Qin Z, Yue S Y, Hu M, Su G 2015 Phys. Chem. Chem. Phys. 17 4854 Google Scholar
[27]	Hong Y, Zhang J, Huang X, Zeng X C 2015 Nanoscale 7 18716 Google Scholar
[28]	Ong Z Y, Cai Y, Zhang G, Zhang Y W 2014 J. Phys. Chem. C 118 25272 Google Scholar
[29]	Zhang Y Y, Pei Q X, Jiang J W, Wei N, Zhang Y W 2016 Nanoscale 8 483 Google Scholar
[30]	Liu B, Bai L, Korznikova E A, Dmitriev S V, Law A W K, Zhou K 2017 J. Phys. Chem. C 121 13876 Google Scholar
[31]	Wei Q, Peng X 2014 Appl. Phys. Lett. 104 251915 Google Scholar
[32]	Yang Z, Zhao J, Wei N 2015 Appl. Phys. Lett. 107 023107 Google Scholar
[33]	Gamil M, Zeng Q H, Zhang Y Y 2020 Phys. Lett. A 384 126784 Google Scholar
[34]	Hatam-Lee S M, Peer-Mohammadi H, Rajabpour A 2021 Mater. Today Commun. 26 101796 Google Scholar
[35]	Mahnama M, Meshkinghalam M, Ozmaian M 2022 J. Phys.: Condens. Matter 34 075403 Google Scholar
[36]	Li T 2021 Physica E 131 114761 Google Scholar
[37]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[38]	Jiang J W 2015 Nanotech. 26 315706 Google Scholar
[39]	Kheirkhah A H, Iranizad E S, Raeisi M, Rajabpour A 2014 Solid State Commun. 177 98 Google Scholar
[40]	Zhang C, Hao X L, Wang C X, Wei N, Rabczuk T 2017 Sci. Rep. 7 41398 Google Scholar
[41]	Zhao J, Jiang J W, Rabczuk T 2013 Appl. Phys. Lett. 103 231913 Google Scholar
[42]	Li T, Tang Z, Huang Z, Yu J 2017 Physica E 85 137 Google Scholar
[43]	Xu K, Fan Z, Zhang J, Wei N, Ala-Nissila T 2018 Modell. Simul. Mater. Sci. Eng. 26 085001 Google Scholar
[44]	Smith B, Vermeersch B, Carrete J, Ou E, Kim J, Mingo N, Akinwande D, Shi L 2017 Adv. Mater. 29 1603756 Google Scholar
[45]	Hu M, Zhang X, Poulikakos D 2013 Phys. Rev. B 87 195417 Google Scholar

[1]	刘秀成, 杨智, 郭浩, 陈颖, 罗向龙, 陈健勇. 金刚石/环氧树脂复合物热导率的分子动力学模拟. , 2023, 72(16): 168102. doi: 10.7498/aps.72.20222270
[2]	李耀隆, 李哲, 李松远, 张任良. 层间共价键和拉伸应变对双层石墨烯纳米带热导率的调控. , 2023, 72(24): 243101. doi: 10.7498/aps.72.20231230
[3]	王甫, 周毅, 高士鑫, 段振刚, 孙志鹏, 汪俊, 邹宇, 付宝勤. 碳化硅中点缺陷对热传导性能影响的分子动力学研究. , 2022, 71(3): 036501. doi: 10.7498/aps.71.20211434
[4]	郑翠红, 杨剑, 谢国锋, 周五星, 欧阳滔. 离子辐照对磷烯热导率的影响及其机制分析. , 2022, 71(5): 056101. doi: 10.7498/aps.71.20211857
[5]	王甫, 周毅, 高士鑫, 段振刚, 孙志鹏, 汪俊(Jun Wang), 邹宇, 付宝勤(Baoqin Fu). 碳化硅中点缺陷对热传导性能影响的分子动力学研究. , 2021, (): . doi: 10.7498/aps.70.20211434
[6]	郑翠红, 杨剑, 谢国锋, 周五星, 欧阳滔. 离子辐照对磷烯热导率的影响及其机制分析. , 2021, (): . doi: 10.7498/aps.70.20211857
[7]	徐文雪, 梁新刚, 徐向华, 祝渊. 交联对硅橡胶热导率影响的分子动力学模拟. , 2020, 69(19): 196601. doi: 10.7498/aps.69.20200737
[8]	兰生, 李焜, 高新昀. 基于分子动力学的石墨炔纳米带空位缺陷的导热特性. , 2017, 66(13): 136801. doi: 10.7498/aps.66.136801
[9]	姜艳, 刘贵立. 剪切形变对硼氮掺杂碳纳米管超晶格电子结构和光学性能的影响. , 2015, 64(14): 147304. doi: 10.7498/aps.64.147304
[10]	常旭. 多层石墨烯的表面起伏的分子动力学模拟. , 2014, 63(8): 086102. doi: 10.7498/aps.63.086102
[11]	郭元军, 刘瑞萍, 杨致, 李秀燕. 过渡元素掺杂对Mo力学性能的第一性原理研究. , 2014, 63(8): 087102. doi: 10.7498/aps.63.087102
[12]	郑伯昱, 董慧龙, 陈非凡. 基于量子修正的石墨烯纳米带热导率分子动力学表征方法. , 2014, 63(7): 076501. doi: 10.7498/aps.63.076501
[13]	张程宾, 程启坤, 陈永平. 分形结构纳米复合材料热导率的分子动力学模拟研究. , 2014, 63(23): 236601. doi: 10.7498/aps.63.236601
[14]	惠治鑫, 贺鹏飞, 戴瑛, 吴艾辉. 硅功能化石墨烯热导率的分子动力学模拟. , 2014, 63(7): 074401. doi: 10.7498/aps.63.074401
[15]	李威, 冯妍卉, 唐晶晶, 张欣欣. 碳纳米管Y形分子结的热导率与热整流现象. , 2013, 62(7): 076107. doi: 10.7498/aps.62.076107
[16]	鲍华. 固体氩的晶格热导率的非简谐晶格动力学计算. , 2013, 62(18): 186302. doi: 10.7498/aps.62.186302
[17]	杨平, 王晓亮, 李培, 王欢, 张立强, 谢方伟. 氮掺杂和空位对石墨烯纳米带热导率影响的分子动力学模拟. , 2012, 61(7): 076501. doi: 10.7498/aps.61.076501
[18]	杨平, 吴勇胜, 许海锋, 许鲜欣, 张立强, 李培. TiO2/ZnO纳米薄膜界面热导率的分子动力学模拟. , 2011, 60(6): 066601. doi: 10.7498/aps.60.066601
[19]	吴国强, 孔宪仁, 孙兆伟, 王亚辉. 氩晶体薄膜法向热导率的分子动力学模拟. , 2006, 55(1): 1-5. doi: 10.7498/aps.55.1
[20]	保文星, 朱长纯. 碳纳米管热传导的分子动力学模拟研究. , 2006, 55(7): 3552-3557. doi: 10.7498/aps.55.3552

计量

文章访问数: 2982
PDF下载量: 49
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板