基于圆柱形非均匀迷宫结构的动态可调定向声辐射

刘昀鹏; 李义丰; 蓝君

doi:10.7498/aps.72.20222186

摘要

构造了一种圆柱形四通道非均匀迷宫结构, 利用该结构设计的圆环型超构材料能够实现动态可调的定向声辐射. 所构造的圆柱形非均匀迷宫结构具有偶极子共振特性, 在偶极子共振频率附近, 声波能够从两个占比较大的扇形通道开口向外辐射, 此时的圆柱形非均匀迷宫结构可近似地看作一个偶极子源. 当圆柱形非均匀迷宫结构围绕圆心进行旋转时, 所形成的偶极子源的位置和向外辐射声波的方向也随之发生改变. 将点声源放置在由18个非均匀迷宫结构组成的圆环型超构材料的中心, 调节圆柱形非均匀迷宫结构的旋转角度, 使各微结构处于导通或截止状态, 从而控制点声源在各个方向上的传播特性, 实现具有动态可调特性的定向声辐射. 此外, 研究了圆柱形非均匀迷宫结构旋转角度对透射声波的影响, 探究了微结构的开关效应, 为构造简易的声定向辐射设备提供了新思路.

关键词:

Abstract

In this work, a cylindrical four-channel non-uniform labyrinth structure is constructed. The ring shaped metamaterial designed by using the rotational anisotropy of the structure can control sound wave and achieve dynamically adjustable directional sound radiation. The cylindrical non-uniform labyrinth structure comprised of four channels has dipole resonance characteristic. At the dipole resonance frequency, sound waves can radiate from the openings of two sector channels that occupy a large proportion. At this time, the cylindrical non-uniform labyrinth structure can be approximately regarded as a dipole sound source. For the cylindrical uniform labyrinth structure, the sound transmission property will not change as it rotates around its center. However, when the cylindrical non-uniform labyrinth structure rotates around its own center, the position of the dipole sound source and the direction of the radiated sound wave also change. Placing a point sound source in the center of the circular metamaterial composed of 18 non-uniform labyrinth structures, and adjusting the rotation angle of the circular non-uniform labyrinth structure so that each structure lies in the conductive or cut-off state, the propagation of the point sound source in all directions can be controlled. The propagation characteristics of these structures are utilized to achieve dynamically adjustable directional sound radiation. In addition, the influence of the rotation angle of the cylindrical non-uniform labyrinth structure on the transmitted sound wave is studied, and the switching effect of the non-uniform cylindrical labyrinth structure in the constructed sound source system is explored, which provides a new idea for constructing simple directional radiation acoustic equipment.

Keywords:

作者及机构信息

1.
南京工业大学计算机科学与技术学院, 南京　211800

2.
近代声学教育部重点实验室, 南京大学声学研究所, 南京　210093

通信作者: 蓝君, junlan@njtech.edu.cn

基金项目: 国家自然科学基金(批准号: 61571222)、江苏省自然科学基金(批准号: BK20210541)江苏省高校自然科学研究项目(批准号: 21KJB140003)和江苏省“六大人才高峰”高层次人才项目资助的课题.

Authors and contacts

1.
College of Computer Science and Technology, Nanjing Tech University, Nanjing 211800, China

2.
Key Laboratory of Modern Acoustics, Ministry of Education, Institute of Acoustics, Nanjing University, Nanjing 210093, China

Corresponding author: Lan Jun, junlan@njtech.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 61571222), the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20210541), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 21KJB140003), and the Six Talent Peaks Project of Jiangsu Province, China.

文章全文 : translate this paragraph

参考文献

[1]	Zhao X, Liu G, Zhang C, Xia D, Lu Z 2018 Appl. Phys. Lett. 113 074101 Google Scholar
[2]	Liang Z, Willatzen M, Li J, et al. 2012 Sci. Rep. 2 859 Google Scholar
[3]	田源, 葛浩, 卢明辉, 陈延峰 2019 68 194301 Google Scholar Tian Y, Ge H, Lu M H, Chen Y F 2019 Acta Phys. Sin. 68 194301 Google Scholar
[4]	Gu Z M, Liang B, Li Y, Zou X Y, Yin L L, Cheng J C 2015 J. Appl. Phys. 117 074502 Google Scholar
[5]	Long H Y, Gao S X, Cheng Y, Liu X J 2018 Appl. Phys. Lett. 112 033507 Google Scholar
[6]	胥强荣, 朱洋, 林康, 沈承, 卢天健 2022 71 214301 Google Scholar Xu Q R, Zhu Y, Lin K, Shen C, Lu T J 2022 Acta Phys. Sin. 71 214301 Google Scholar
[7]	Polychronopoulos S, Memoli G 2020 Sci. Rep. 10 4254 Google Scholar
[8]	Walker E L, Jin Y Q, Reyes D, Neogi A 2020 Nat. Commun. 11 5967 Google Scholar
[9]	Yang Z, Mei J, Yang M, et al. 2008 Phys. Rev. Lett. 101 204301 Google Scholar
[10]	Ma G, Sheng P 2016 Sci. Adv. 2 e1501595 Google Scholar
[11]	Tan Y, Liang B, Cheng J C 2022 Chin. Phys. B 31 034303 Google Scholar
[12]	Song K, Kim J, Hur S, et al. 2016 Sci. Rep. 6 32300 Google Scholar
[13]	Esfahlani H, Karkar S, Lissek H, Mosig J R 2016 J. Acoust. Soc. Am. 139 3259 Google Scholar
[14]	Qian J, Sun H, Yuan S, Liu X 2019 Appl. Phys. Lett. 114 013506 Google Scholar
[15]	Tang S, Han J N, Wen T D 2018 AIP Adv. 8 085312 Google Scholar
[16]	Zhang Z W, Tian Y, Wang Y H, Gao S X, Cheng Y, Liu X J, Christensen J 2018 Adv. Mater. 30 1803229 Google Scholar
[17]	Craig S R, Wang B H, Su X S, Banerjee D, Welch P J, Yip M C, Hu Y H, Shi C Z 2022 J. Acoust. Soc. Am. 151 1722 Google Scholar
[18]	Bai L, Song G Y, Jiang W X, Cheng Q, Cui T J 2019 Appl. Phys. Lett. 115 231902 Google Scholar
[19]	Dai H Q, Xia B Z, Yu D J 2017 J. Appl. Phys. 122 065103 Google Scholar
[20]	Chen Z Y, Wang X Y, Lim C W 2022 J. Appl. Phys. 131 185112 Google Scholar
[21]	Jiang X, Zhang L K, Liang B, Zou X Y, Cheng J 2015 Appl. Phys. Lett. 107 093506 Google Scholar
[22]	Chen X, Cai L, Wen J H 2018 Chin. Phys. B 27 057803 Google Scholar
[23]	Ju F F, Cheng Y, Liu X J 2018 Sci. Rep. 8 11113 Google Scholar
[24]	Li W P, Liu F M, Mei L R, Ke M Z, Liu Z Y 2019 Appl. Phys. Lett. 114 061904 Google Scholar
[25]	蔡成欣, 陈韶赓, 王学梅, 梁俊燕, 王兆宏 2020 69 134302 Google Scholar Cai C X, Chen S G, Wang X M, Liang J Y, Wang Z H 2020 Acta Phys. Sin. 69 134302 Google Scholar
[26]	Zhang Z W, Cheng Y, Liu X J, Christensen J 2019 Phys. Rev. B 99 224104 Google Scholar
[27]	Lu G X, Ding E L, Wang Y Y, Peng X Y, Cui J, Liu X Z, Liu X J 2017 Appl. Phys. Lett. 110 123507 Google Scholar
[28]	Li Y, Liang B, Zou X Y, Cheng J C 2013 Appl. Phys. Lett. 103 063509 Google Scholar
[29]	Zhang J, Cheng Y, Liu X J 2017 Appl. Phys. Lett. 110 233502 Google Scholar
[30]	Liu C, Long H Y, Zhou C, Cheng Y, Liu X J 2020 Sci. Rep. 10 1519 Google Scholar
[31]	Zhou C, Yuan B, Cheng Y, Liu X J 2016 Appl. Phys. Lett. 108 063501 Google Scholar
[32]	Zhang J, Rui W, Ma C R, et al. 2021 Nat. Commun. 12 3670 Google Scholar

施引文献

图 1 (a)圆柱形非均匀迷宫结构的截面图; (b)微结构的等效模型

Fig. 1. (a) Cross section of the cylindrical non-uniform labyrinth structure; (b) equivalent model of microstructure.

下载: 全尺寸图片幻灯片

图 2 圆柱形非均匀迷宫结构的(a)单极子模式声压场图和(b)偶极子模式声压场图; 等效模型的(c)单极子模式声压场图和(d)偶极子模式声压场图

Fig. 2. (a) Monopole mode and (b) dipole mode sound pressure field diagrams of cylindrical non-uniform labyrinth structure; (c) monopole mode and (d) dipole mode sound pressure field diagrams of equivalent model.

下载: 全尺寸图片幻灯片

图 3 (a)平面波作用下的非均匀迷宫结构示意图; (b)检测点A, B, C和D处的声压随频率的变化图

Fig. 3. (a) Schematic diagram of non-uniform labyrinth structure under the plane wave; (b) variation diagram of sound pressure as a function of frequency at test points A, B, C and D.

下载: 全尺寸图片幻灯片

图 4 平面波作用下的非均匀迷宫结构的散射声场图　(a)原始微结构; (b)结构旋转60°; (c)结构旋转70°; (d)结构旋转140°, 图4(a)—(d)中的右下角插图为结构特写; (e)实心刚性圆; (f)微结构逆时针旋转不同角度情况下的声辐射图

Fig. 4. Scattering sound field diagram of non-uniform labyrinth structure under the plane wave: (a) Original microstructure; (b) the structure rotates by 60°; (c) the structure rotates by 70°; (d) the structure rotates by 140°, and the insets at the lower right corner of Figure 4(a)-(d) are the clear views of structure; (e) solid rigid circle; (f) acoustic radiation patterns of microstructures under different counterclockwise rotation angles.

下载: 全尺寸图片幻灯片

图 5 (a)由18个非均匀迷宫结构构成的圆环型超构材料; (b)圆环型超构材料中求取微结构中心到点声源的距离D的具体示意图; (c)单个微结构处于打开状态时的声压场分布图; (d)两个指定的微结构同时处于打开状态时的声压场分布图

Fig. 5. (a) Toroidal metamaterial constructed with 18 non-uniform labyrinth structures; (b) the specific schematic diagram of the distance D from the center of the microstructure to the point sound source in the ring type metamaterial; (c) sound pressure field distribution diagram when a single microstructure is in the open state; (d) sound pressure field distribution diagram when two designated microstructures are in the open state at the same time.

下载: 全尺寸图片幻灯片

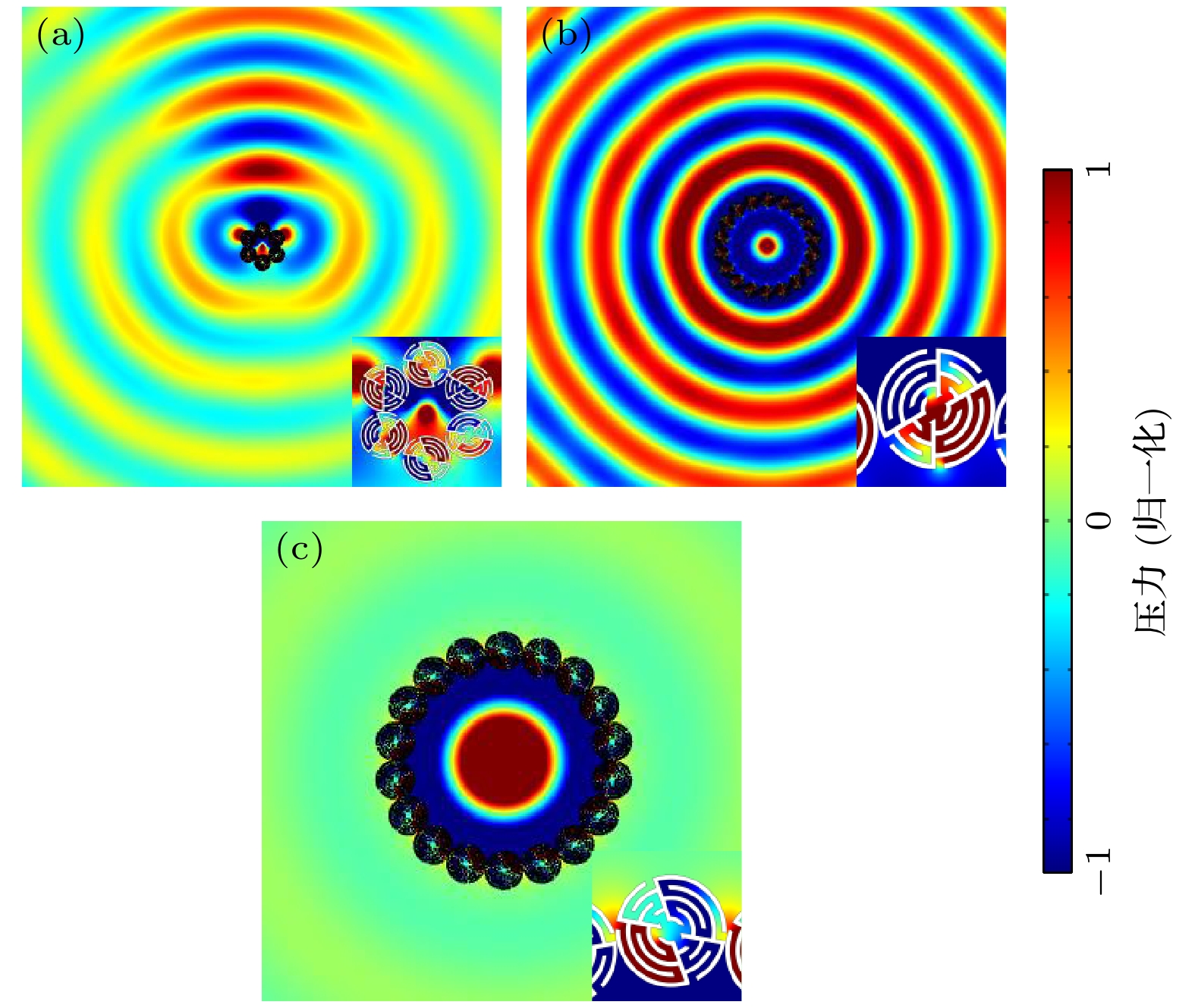
图 6 (a)由6个微结构构成的圆环型超构材料实现的声定向辐射; (b)圆环型超构材料的18个微结构全部处于打开状态时的声压场分布图; (c)圆环型超构材料的18个微结构全部处于关闭状态时的声压场分布图

Fig. 6. (a) Acoustic directional radiation realized by toroidal metamaterials composed of 6 microstructures; (b) sound pressure field distribution diagram when all the 18 microstructures of the toroidal metamaterial are in the open state; (c) sound pressure field distribution diagram when all the 18 microstructures of the toroidal metamaterial are in the closed state.

下载: 全尺寸图片幻灯片

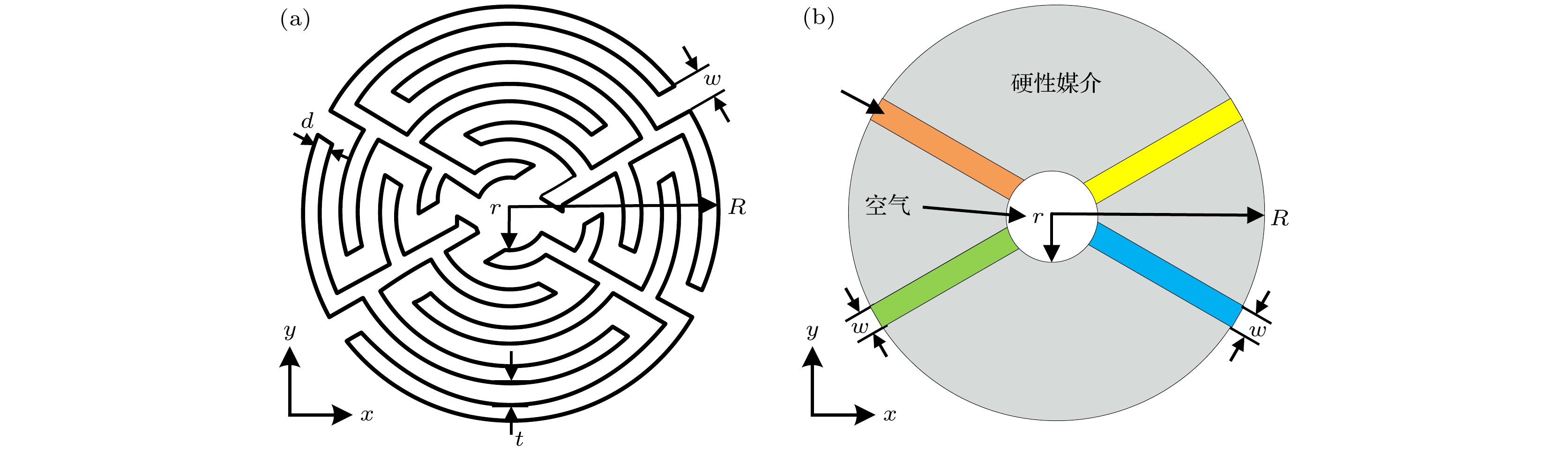
表 1 圆柱形非均匀迷宫结构的结构参数

Table 1. Structural parameters of cylindrical non-uniform labyrinth structure.

参数类型数值/cm

通道口宽度w 0.42
壁厚d 0.25
通道宽度t 0.306
外圆半径R 3
内圆半径r 0.526

下载: 导出CSV

map

[1]	Zhao X, Liu G, Zhang C, Xia D, Lu Z 2018 Appl. Phys. Lett. 113 074101 Google Scholar
[2]	Liang Z, Willatzen M, Li J, et al. 2012 Sci. Rep. 2 859 Google Scholar
[3]	田源, 葛浩, 卢明辉, 陈延峰 2019 68 194301 Google Scholar Tian Y, Ge H, Lu M H, Chen Y F 2019 Acta Phys. Sin. 68 194301 Google Scholar
[4]	Gu Z M, Liang B, Li Y, Zou X Y, Yin L L, Cheng J C 2015 J. Appl. Phys. 117 074502 Google Scholar
[5]	Long H Y, Gao S X, Cheng Y, Liu X J 2018 Appl. Phys. Lett. 112 033507 Google Scholar
[6]	胥强荣, 朱洋, 林康, 沈承, 卢天健 2022 71 214301 Google Scholar Xu Q R, Zhu Y, Lin K, Shen C, Lu T J 2022 Acta Phys. Sin. 71 214301 Google Scholar
[7]	Polychronopoulos S, Memoli G 2020 Sci. Rep. 10 4254 Google Scholar
[8]	Walker E L, Jin Y Q, Reyes D, Neogi A 2020 Nat. Commun. 11 5967 Google Scholar
[9]	Yang Z, Mei J, Yang M, et al. 2008 Phys. Rev. Lett. 101 204301 Google Scholar
[10]	Ma G, Sheng P 2016 Sci. Adv. 2 e1501595 Google Scholar
[11]	Tan Y, Liang B, Cheng J C 2022 Chin. Phys. B 31 034303 Google Scholar
[12]	Song K, Kim J, Hur S, et al. 2016 Sci. Rep. 6 32300 Google Scholar
[13]	Esfahlani H, Karkar S, Lissek H, Mosig J R 2016 J. Acoust. Soc. Am. 139 3259 Google Scholar
[14]	Qian J, Sun H, Yuan S, Liu X 2019 Appl. Phys. Lett. 114 013506 Google Scholar
[15]	Tang S, Han J N, Wen T D 2018 AIP Adv. 8 085312 Google Scholar
[16]	Zhang Z W, Tian Y, Wang Y H, Gao S X, Cheng Y, Liu X J, Christensen J 2018 Adv. Mater. 30 1803229 Google Scholar
[17]	Craig S R, Wang B H, Su X S, Banerjee D, Welch P J, Yip M C, Hu Y H, Shi C Z 2022 J. Acoust. Soc. Am. 151 1722 Google Scholar
[18]	Bai L, Song G Y, Jiang W X, Cheng Q, Cui T J 2019 Appl. Phys. Lett. 115 231902 Google Scholar
[19]	Dai H Q, Xia B Z, Yu D J 2017 J. Appl. Phys. 122 065103 Google Scholar
[20]	Chen Z Y, Wang X Y, Lim C W 2022 J. Appl. Phys. 131 185112 Google Scholar
[21]	Jiang X, Zhang L K, Liang B, Zou X Y, Cheng J 2015 Appl. Phys. Lett. 107 093506 Google Scholar
[22]	Chen X, Cai L, Wen J H 2018 Chin. Phys. B 27 057803 Google Scholar
[23]	Ju F F, Cheng Y, Liu X J 2018 Sci. Rep. 8 11113 Google Scholar
[24]	Li W P, Liu F M, Mei L R, Ke M Z, Liu Z Y 2019 Appl. Phys. Lett. 114 061904 Google Scholar
[25]	蔡成欣, 陈韶赓, 王学梅, 梁俊燕, 王兆宏 2020 69 134302 Google Scholar Cai C X, Chen S G, Wang X M, Liang J Y, Wang Z H 2020 Acta Phys. Sin. 69 134302 Google Scholar
[26]	Zhang Z W, Cheng Y, Liu X J, Christensen J 2019 Phys. Rev. B 99 224104 Google Scholar
[27]	Lu G X, Ding E L, Wang Y Y, Peng X Y, Cui J, Liu X Z, Liu X J 2017 Appl. Phys. Lett. 110 123507 Google Scholar
[28]	Li Y, Liang B, Zou X Y, Cheng J C 2013 Appl. Phys. Lett. 103 063509 Google Scholar
[29]	Zhang J, Cheng Y, Liu X J 2017 Appl. Phys. Lett. 110 233502 Google Scholar
[30]	Liu C, Long H Y, Zhou C, Cheng Y, Liu X J 2020 Sci. Rep. 10 1519 Google Scholar
[31]	Zhou C, Yuan B, Cheng Y, Liu X J 2016 Appl. Phys. Lett. 108 063501 Google Scholar
[32]	Zhang J, Rui W, Ma C R, et al. 2021 Nat. Commun. 12 3670 Google Scholar

[1]	董石泉, 何安, 刘伟, 薛存. 磁悬浮系统中多芯复合Nb₃Sn超导线磁通跳跃的可调性研究. , 2023, 72(1): 017401. doi: 10.7498/aps.72.20221252
[2]	周丽丽, 胡欣悦, 穆中林, 张蕤, 郑悦. 任意方向电偶极子在水平分层受限空间中的远区辐射场求解. , 2022, 71(20): 200301. doi: 10.7498/aps.71.20220545
[3]	吴双林, 李整林, 秦继兴, 王梦圆, 董凡辰. 东印度洋热带偶极子对声会聚区影响分析. , 2022, 71(13): 134301. doi: 10.7498/aps.71.20212355
[4]	张翔宇, 刘会刚, 康明, 刘波, 刘海涛. 金属-介质-金属多层结构可调谐Fabry-Perot共振及高灵敏折射率传感. , 2021, 70(14): 140702. doi: 10.7498/aps.70.20202058
[5]	聂长文, 吴瀚舟, 王书豪, 蔡园园, 宋树, SokolovOleg, BichurinM. I., 汪尧进. 磁电电压可调电感器的理论设计与可调性优化. , 2021, 70(24): 247501. doi: 10.7498/aps.70.20210899
[6]	郭威, 杨德森. 非均匀波导中的声聚焦. , 2020, 69(7): 074301. doi: 10.7498/aps.69.20191854
[7]	廖涛, 孙小伟, 宋婷, 田俊红, 康太凤, 孙伟彬. 新型二维压电声子晶体板带隙可调性研究. , 2018, 67(21): 214208. doi: 10.7498/aps.67.20180611
[8]	许松, 唐晓明, 苏远大. 横向各向同性固体材料中含定向非均匀体的有效弹性模量. , 2015, 64(20): 206201. doi: 10.7498/aps.64.206201
[9]	宋永佳, 胡恒山. 含定向非均匀体固体材料的横观各向同性有效弹性模量. , 2014, 63(1): 016202. doi: 10.7498/aps.63.016202
[10]	张思文, 吴九汇. 局域共振复合单元声子晶体结构的低频带隙特性研究. , 2013, 62(13): 134302. doi: 10.7498/aps.62.134302
[11]	洪清泉, 仲伟博, 余燕忠, 蔡植善, 陈木生, 林顺达. 电偶极子在磁各向异性介质中的辐射功率. , 2012, 61(16): 160302. doi: 10.7498/aps.61.160302
[12]	尚勋忠, 陈威, 曹万强. 弛豫铁电体介电可调性的研究. , 2012, 61(21): 217701. doi: 10.7498/aps.61.217701
[13]	魏琦, 程营, 刘晓峻. 点缺陷阵列对声子晶体波导定向辐射性能的影响. , 2011, 60(12): 124301. doi: 10.7498/aps.60.124301
[14]	梁子长, 金亚秋. 非均匀散射层矢量辐射传输(VRT)方程高阶散射解的迭代法. , 2003, 52(2): 247-255. doi: 10.7498/aps.52.247
[15]	张必达, 王卫东, 宋枭禹, 俎栋林, 吕红宇, 包尚联. 磁共振现代射频脉冲理论在非均匀场成像中的应用. , 2003, 52(5): 1143-1150. doi: 10.7498/aps.52.1143
[16]	王鹏谦, 田测产, 孙（马匋）亨. 在Ne的第一共振态以下通过四波和频产生可调谐VUV相干辐射. , 1997, 46(2): 300-305. doi: 10.7498/aps.46.300
[17]	李芳昱, 罗俊, 唐孟希. 轴对称非均匀弹性介质中引力波对声子的作用效应. , 1994, 43(8): 1217-1225. doi: 10.7498/aps.43.1217
[18]	庞根弟, 蔡建华. 非均匀无序系统的声子局域化. , 1988, 37(4): 688-690. doi: 10.7498/aps.37.688
[19]	孙伯勤, 叶朝辉. 魔角旋转情形下固体的非均匀相互作用. , 1986, 35(3): 329-337. doi: 10.7498/aps.35.329
[20]	卫崇德, 赵士平, 薛立新. 声子注入下超导锡膜的非均匀态. , 1985, 34(10): 1368-1372. doi: 10.7498/aps.34.1368

计量

文章访问数: 3421
PDF下载量: 63
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

基于圆柱形非均匀迷宫结构的动态可调定向声辐射