多场耦合Fe基合金巨磁阻抗效应调控机制

张建强; 秦彦军; 方峥; 范晓珍; 马云; 李文忠; 杨慧雅; 邝富丽; 翟耀; 师应龙; 党文强; 叶慧群; 方允樟

doi:10.7498/aps.71.20221376

摘要

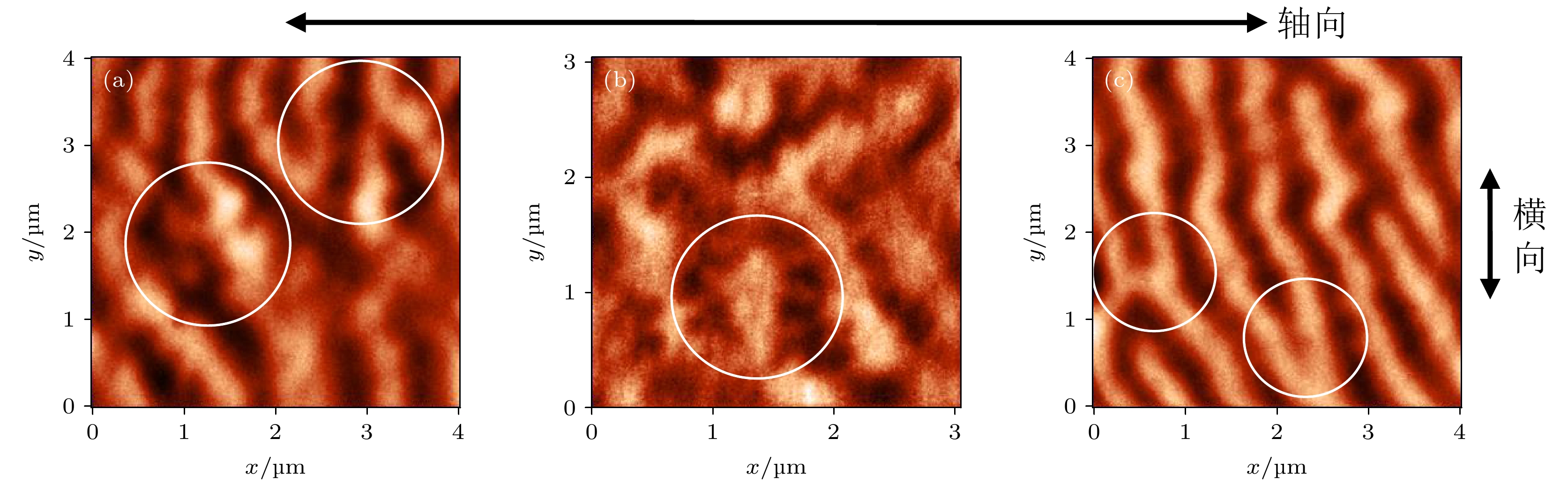
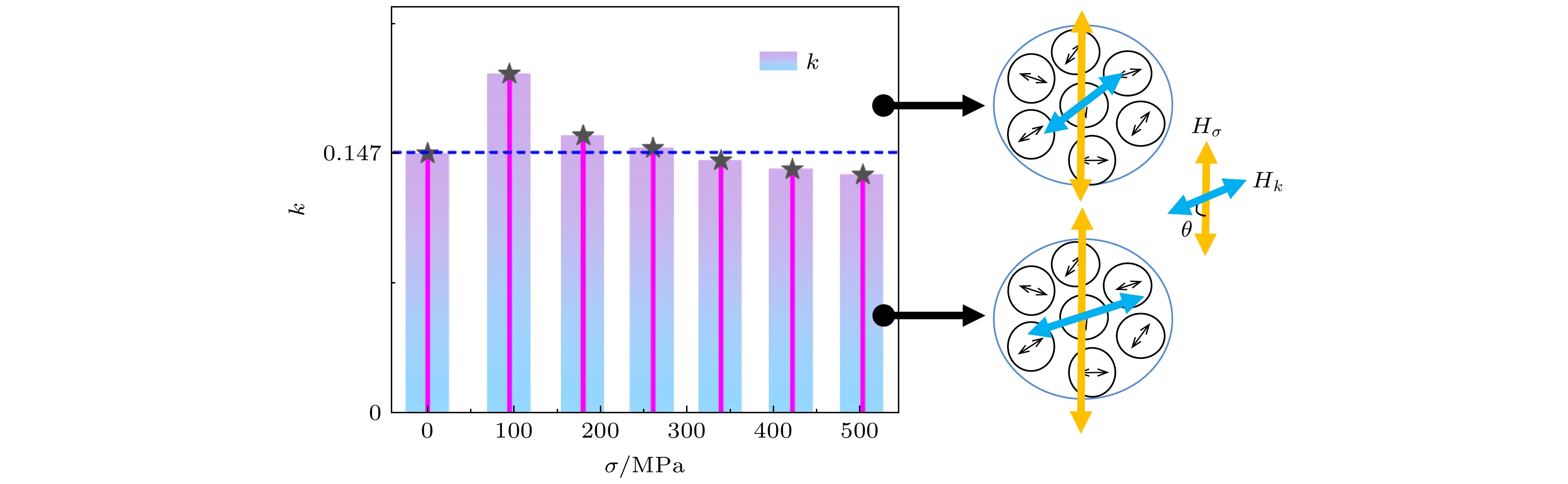
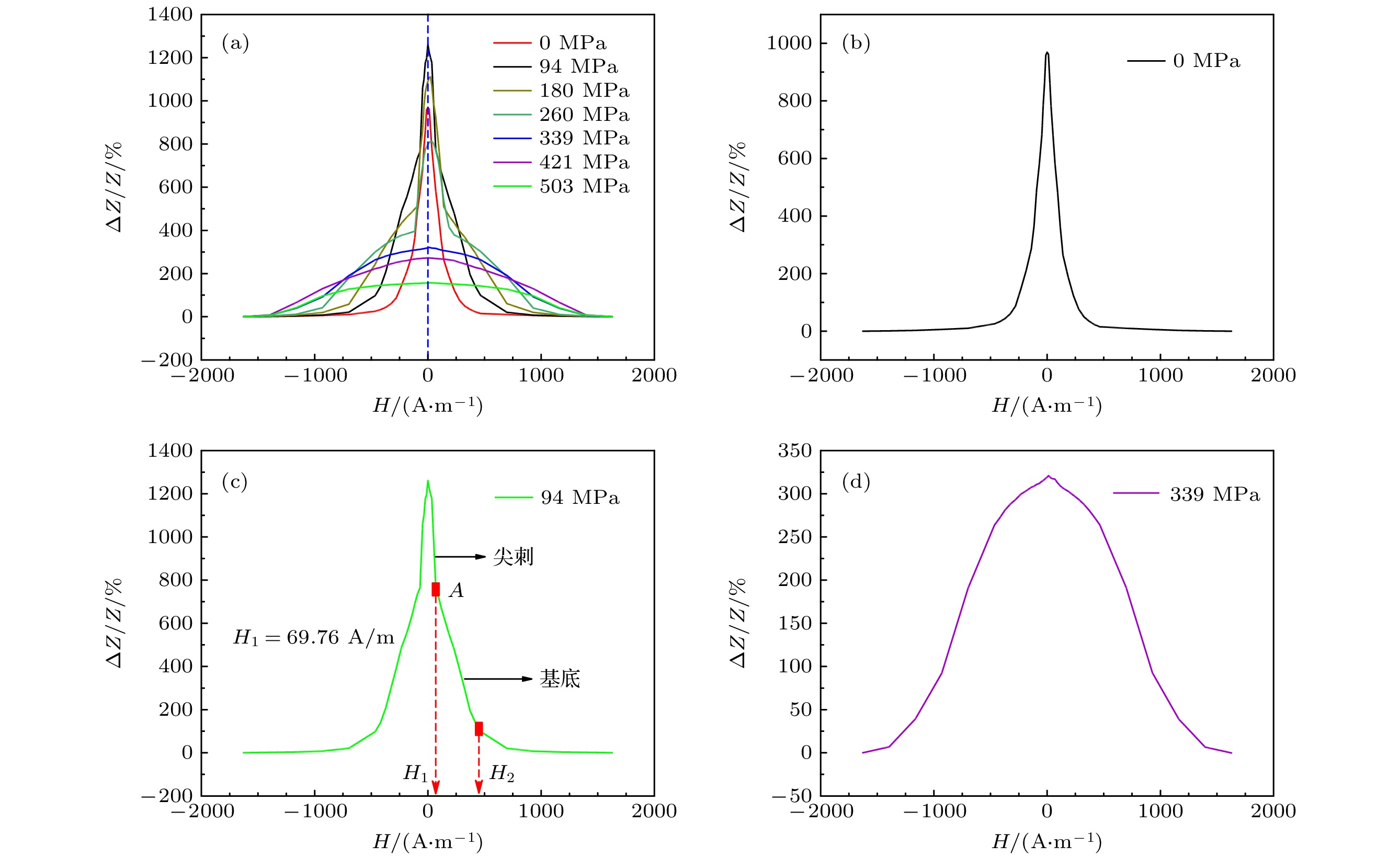
Fe基合金性能优异, 是首选的“双绿色”节能材料, 在电力电子信息领域具有重要的应用价值. 本文对单辊快淬制备的Fe_64.8Co_7.2Nb₄Si_4.8B_19.2非晶薄带实施多场耦合热处理(电流张应力退火), 采用阻抗仪和磁力显微镜观测薄带纵向驱动巨磁阻抗效应及磁畴结构, 结合X射线衍射、随机各向异性模型和数值拟合分析薄带的磁晶各向异性和应力各向异性, 提出磁各向异性竞争因子k, 从磁各向异性角度研究合金带巨磁阻抗效应调控机制. 结果表明, $ k \leqslant 0.147 $的薄带展现出“单峰”和“穹顶”状的巨磁阻抗效应, 且具有较规则的横向磁畴结构; 而$ k \gt 0.147 $的薄带展现出“尖刺+穹顶”状巨磁阻抗效应, 同时在较不规则的横向畴畴壁处观测到新畴的形核和分裂, 这为磁各向异性的竞争抑制作用提供了佐证. 因此, 本研究认为多场耦合热处理Fe_64.8Co_7.2Nb₄Si_4.8B_19.2合金薄带展现出良好的应力敏感特性可由磁各向异性的竞争抑制作用解释, 它是材料巨磁阻抗效应实现调控的主要原因, 在调制优化材料磁性能方面具有良好的应用前景.

关键词:

Abstract

Fe-based amorphous and nanocrystalline alloys are considered as the preferred dual-green energy-saving materials due to their unique magnetic properties, such as high permeability, low coercivity, and near-zero saturation magnetostriction. As such, they have received extensive attention in applications like magnetic core material for high-frequency transformers, common model chokes, ground fault interrupters, and rotors in motors, over the past decades. In this work, Fe_64.8Co_7.2Nb₄Si_4.8B_19.2 (in atom percent) amorphous alloy ribbons are prepared by using the single roller quenching method, then subsequently subjected to multi-field coupling heating treatment in the air which includes heating by Joule heating effect and tensile stress field. Furthermore, the longitudinally driven giant magneto-impedance effect and magnetic domain structures of ribbons are observed by using 4294A impedance analyzer and magnetic force microscopy, respectively. The magneto-crystalline anisotropy field and stress anisotropy field of ribbons are analyzed by using X-ray diffraction, random anisotropy model, and numerical fitting. Meanwhile, the concept of magnetic anisotropy competing factor (k) is proposed, from the viewpoint of magnetic anisotropy, a mechanism for regulating giant magneto-impedance effect of ribbons prepared with multi-field coupling is studied. It is found that the longitudinally driven giant magneto-impedance effect gradually transforms from the single peak to dome-like with tensile stress increasing. However, a spike and dome-like giant magneto-impedance effect appears during such transformation, which is composed of two parts: spike-like top and dome-like base. Based on the magnetic domain structure of ribbons, it is found that the typical stress-annealed transversal magnetic domain structure is observed in ribbons of $k \leqslant 0.147$, while nucleation and splitting phenomenon of new domains are observed at the transversal magnetic domain wall in ribbons of k > 0.147. Both longitudinally driven giant magneto-impedance effect and domain structures provide evidence to support the competing inhibition effect of magnetic anisotropy which exists in Fe-based alloy ribbon. Therefore, it is suggested that Fe-based alloys exhibit excellent stress-sensitive properties that can be understood by the competing inhibition effects of magnetic anisotropy. It is further shown that the competing inhibition effect of magnetic anisotropy is the main reason for regulating the giant magneto-impedance effect of soft magnetic materials. This multi-field coupling Fe-based alloy has good application prospects in regulating magnetic properties of magnetic materials.

Keywords:

作者及机构信息

1.
浙江师范大学物理与电子信息工程学院, 金华　321004

2.
天水师范学院电子信息与电气工程学院, 天水　741001

3.
浙江师范大学, 浙江省固态光电器件重点实验室, 金华　321004

4.
浙江旅游职业学院, 杭州　311231

通信作者: 张建强, zhjian8386@163.com ; 方允樟, fyz@zjnu.cn

基金项目: 新疆维吾尔自治区重点专项研发项目 (批准号: KYZ04Y21100)、国家自然科学基金地区科学基金 (批准号: 12064037)、甘肃省科技计划项目(批准号: 21JR1RE288)、新疆维吾尔自治区自然科学基金(批准号: 2021D01B47)和天水师范学院高级别预研项目 (批准号: GJB2021-09) 资助的课题.

Authors and contacts

1.
College of Physics and Electronic Information Engineering, Zhejiang Normal University, Jinhua 321004, China

2.
College of Electronic Information and Electrical Engineering, Tianshui Normal University, Tianshui 741001, China

3.
Key Laboratory of Solid State Optoelectronic Devices of Zhejiang Povince, Zhejiang Normal University, Jinhua 321004, China

4.
Tourism College of Zhejiang, Hangzhou 311231, China

Corresponding author: Zhang Jian-Qiang, zhjian8386@163.com ; Fang Yun-Zhang, fyz@zjnu.cn

Funds: Project supported by the Key Specialized Research and Development Program of Xinjiang Uygur Autonomous Region, China (Grant No. KYZ04Y21100), the Fund for Less Developed Regions of the National Natural Science Foundation of China (Grant No. 12064037), the Program on Science and Technology of Gansu Province, China (Grant No. 21JR1RE288), the Natural Science Foundation of Xinjiang Uygur Autonomous Region, China (Grant No. 2021D01B47), and the High Level Pre-research Program of Tianshui Normal University, China (Grant No. GJB2021-09) .

文章全文 : translate this paragraph

参考文献

[1]	Duwez P, Willens R H, Klement W 1960 J. Appl. Phys. 31 1136
[2]	汪卫华, 张哲峰 2021 金属学报 57 1 Google Scholar Wang W H, Zhang Z F 2021 Acta Metall. Sin. 57 1 Google Scholar
[3]	姚可夫, 施凌翔, 陈双琴, 邵洋, 陈娜, 贾蓟丽 2018 67 016101 Google Scholar Yao K F, Shi L X, Chen S Q, Shao Y, Chen N, Jia J L 2018 Acta Phys. Sin. 67 016101 Google Scholar
[4]	Panina L V, Mohri K 1994 Appl. Phys. Lett. 65 1189
[5]	Mohri K, Kawashiwa K, Yoshida H, Panina L V 1992 IEEE. Trans. Magn. 28 3150 Google Scholar
[6]	Indaa K, Mohri K, Inuzuka K 1994 IEEE. Trans. Magn. 30 4623 Google Scholar
[7]	Panina L V, Mohri K, Uchiyama T, Noda M, Bushida 1995 IEEE. Trans. Magn. 31 1249 Google Scholar
[8]	Kawashima K, Kohzawa K, Yoshida H, Mohri M 1993 IEEE. Trans. Magn. 29 3168 Google Scholar
[9]	杨介信, 杨夑龙, 陈国, 蒋可玉, 沈国土, 胡炳元, 金若鹏 1998 中国科学 43 1051 Google Scholar Yang J X, Yang X L, Chen G, Jiang K Y, Shen G T, Hu B Y, Jin R P 1998 Chin. Sci. Bull. 43 1051 Google Scholar
[10]	Gong W Y, Wu Z M, Lin H, Yang J X, Zhao Z J 2008 J. Magn. Magn. Mater. 320 1553 Google Scholar
[11]	方允樟, 许启明, 叶慧群, 郑金菊, 范晓珍, 潘日敏, 马云, 李文忠 2011 功能材料 42 1083 Fang Y Z, Xu Q M, Ye H Q, Zheng J J, Fan X Z, Pan R M, Ma Y, Li W Z 2011 Funct. Mater. 42 1083
[12]	Zhukov A, Ipatov M, Churyukanova M, Talaat A, Blanco J M, Zhukova V 2017 J. Alloys Compd. 727 887 Google Scholar
[13]	Herzer G 2013 Acta. Mater. 61 718 Google Scholar
[14]	Zhukov A, Ipatov M, Corte-Leon P, Gonzalez-Legarreta L, Churyukanova M, Blanco J M, Gonzalez J, Taskaev S, Hernando B, Zhukova V 2020 J. Alloys Compd. 814 152225 Google Scholar
[15]	Corte-Leon P, Zhukova V, Ipatov M, Blanco J M, Gonzalez J, Zhukov A 2019 Intermetallics 105 92 Google Scholar
[16]	Zhukova V, Blanco J M, Ipatov M, Gonzalez J, Churyukanova M, Zhukov A 2018 Scr. Mater. 142 10 Google Scholar
[17]	Phan M H, Peng H X 2008 Prog. Mater. Sci. 53 323 Google Scholar
[18]	Ohnuma M, Yanai T, Hono K, Nakano M, Fukunaga H, Yoshizawa Y, Herzer G 2010 J. Appl. Phys. 108 093927 Google Scholar
[19]	Kernion S J, Ohodnicki P R, Grossmann J J, Leary A, Shen S, Keylin V, Huth J F, Horwath J, Lucas M S, McHenry M E 2012 Appl. Phys. Lett. 101 102408 Google Scholar
[20]	Iannotti V, Amoruso S, Ausanio G, Wang X, Lanotte L, Barone A C, Margaris G, Trohidou K N, Fiorani D 2011 Phys. Rev. B 83 214422 Google Scholar
[21]	Bolyachkin A S, Volegov A S, Kudrevatykh N V 2015 J. Magn. Magn. Mater. 378 362 Google Scholar
[22]	Muscas G, Concas G, Laureti S, Testa A M, Mathieu R, De Toro J A, Cannas C, Musinu A, Novak M A, Sangregorio C, Lee S S, Peddis D 2018 Phys. Chem. Chem. Phys. 20 28634 Google Scholar
[23]	纪松, 杨国斌, 王润 1996 45 2061 Google Scholar Ji S, Yang G B, Wang R 1996 Acta Phys. Sin. 45 2061 Google Scholar
[24]	Hinokihara T, Miyashita S 2021 Phys. Rev. B 103 054421 Google Scholar
[25]	Hofmann B, Kronmüller H 1996 J. Magn. Magn. Mater. 152 91 Google Scholar
[26]	Herzer G 1995 Scr. Metall. Mater. 33 1741 Google Scholar
[27]	Hernando A, Kulik T 1994 Phys. Rev. B 49 7064 Google Scholar
[28]	张建强, 路飞平, 赵小龙, 何林芳 2019 磁性材料及器件 50 9 Zhang J Q, Lu F P, Zhao X L, He L F 2019 J. Magn. Mater. Device 50 9
[29]	Jaafar M, Pablo-Navarro A, Berganza E, Ares P, Magén C, Masseboeuf A, Gatel C, Snoeck E, Gómez-Herrero J, Teresa J M, Asenjo A 2020 Nanoscale 12 10090 Google Scholar

施引文献

图 1 Fe基合金LDGMI效应　(a) 0−503 MPa退火; (b) “单峰”状; (c) “尖刺+穹顶”状; (d) “穹顶”状

Fig. 1. LDGMI effect of Fe-based alloy: (a) Annealed with different tensile stress (0−503 MPa); (b) single peak shape; (c) spike and dome shape; (d) dome shape.

下载: 全尺寸图片幻灯片

图 2 Fe基合金最大磁阻抗比及磁灵敏度与退火应力关系

Fig. 2. Maximum magneto-impedance ratio and magnetic sensitivity of Fe-based alloys ribbons as a function of annealing tensile stress.

下载: 全尺寸图片幻灯片

图 3 MFC热处理Fe基合金带的XRD谱

Fig. 3. XRD pattern of Fe-based alloy heated with MFC method.

下载: 全尺寸图片幻灯片

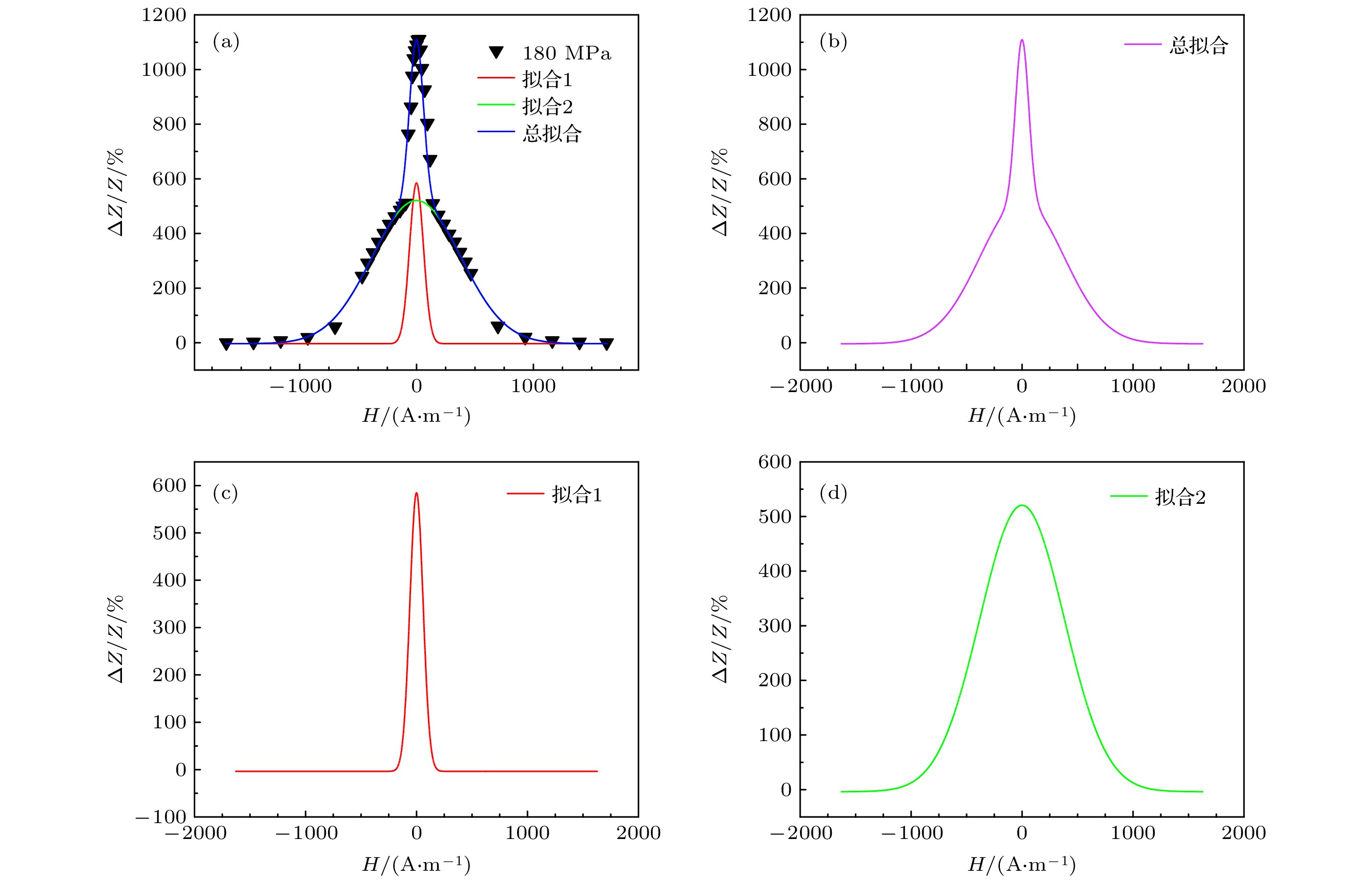
图 4 “尖刺+穹顶”状LDGMI曲线高斯拟合　(a) 180 MPa退火合金带LDGMI效应拟合; (b) 总拟合曲线; (c) “尖刺”状; (d) “穹顶”状

Fig. 4. Gaussian fitting of “spike and dome” like LDGMI effect curve: (a) Fitting curve of LDGMI effect for Fe-based alloy ribbon annealed with tensile stress of 180 MPa; (b) the whole fitting curve; (c) spike shape; (d) dome shape.

下载: 全尺寸图片幻灯片

图 5 应力各向异性场和磁晶各向异性场与应力关系

Fig. 5. Stress anisotropy field and the magneto-crystalline anisotropy field of Fe-based alloy ribbons as a function of annealing tensile stress.

下载: 全尺寸图片幻灯片

图 6 不同退火应力下, MFC热处理Fe基合金磁畴结构图　(a) 0 MPa; (b) 94 MPa; (c) 339 MPa

Fig. 6. Domain structure patterns of Fe-based alloy ribbons heated by MFC under different tensile stress: (a) 0 MPa; (b) 94 MPa; (c) 339 MPa.

下载: 全尺寸图片幻灯片

图 7 Fe基合金磁各向异性竞争抑制作用模型示意图

Fig. 7. Schematic diagram of the competing inhibition model of magnetic anisotropy in Fe-based alloys.

下载: 全尺寸图片幻灯片

表 1 未加张应力退火Fe基合金带的结构参数和磁学量参数

Table 1. Structural and magnetic parameters of Fe-based alloy annealed without tensile stress.

	参数/单位	数值
结构参数	D/nm	16.20
结构参数	x/%	53.12
磁学量参数	K₁/(J·m^–3)	8000^[26]
	A/(J·m^–1)	10^–11[26]
	J_s/T	1.24^[25]
	〈K₁〉/(J·m^–3)	8.36
	H_k/(A·m^–1)	13.48
	H_σ/(A·m^–1)	91.51
	k	0.147

下载: 导出CSV

表 2 MFC热处理Fe基合金带LDGMI效应曲线拟合DPGF参数和磁学参数

Table 2. DPGF parameters of LDGMI effect curves and magnetic parameters of Fe-based alloy heated by MFC method.

应力 σ/MPa	DPGF参数			磁各向异性场				实验值
应力 σ/MPa	W₁	W₂	R	H_k/(A·m^–1)	H_σ/(A·m^–1)	H_eff/(A·m^–1)	k	H_eff/(A·m^–1)
94	105.64	549.94	0.997	52.82	274.97	280.00	0.195	—
180	139.97	893.04	0.986	69.98	446.52	451.97	0.157	—
260	177.79	1183.86	0.975	88.90	591.93	598.57	0.150	—
339	—	—	—	106.5	745.23	752.80	0.143	772.52
421	—	—	—	124.32	899.94	908.49	0.138	903.81
503	—	—	—	142.36	1056.56	1066.11	0.135	1012.43

下载: 导出CSV

map

[1]	Duwez P, Willens R H, Klement W 1960 J. Appl. Phys. 31 1136
[2]	汪卫华, 张哲峰 2021 金属学报 57 1 Google Scholar Wang W H, Zhang Z F 2021 Acta Metall. Sin. 57 1 Google Scholar
[3]	姚可夫, 施凌翔, 陈双琴, 邵洋, 陈娜, 贾蓟丽 2018 67 016101 Google Scholar Yao K F, Shi L X, Chen S Q, Shao Y, Chen N, Jia J L 2018 Acta Phys. Sin. 67 016101 Google Scholar
[4]	Panina L V, Mohri K 1994 Appl. Phys. Lett. 65 1189
[5]	Mohri K, Kawashiwa K, Yoshida H, Panina L V 1992 IEEE. Trans. Magn. 28 3150 Google Scholar
[6]	Indaa K, Mohri K, Inuzuka K 1994 IEEE. Trans. Magn. 30 4623 Google Scholar
[7]	Panina L V, Mohri K, Uchiyama T, Noda M, Bushida 1995 IEEE. Trans. Magn. 31 1249 Google Scholar
[8]	Kawashima K, Kohzawa K, Yoshida H, Mohri M 1993 IEEE. Trans. Magn. 29 3168 Google Scholar
[9]	杨介信, 杨夑龙, 陈国, 蒋可玉, 沈国土, 胡炳元, 金若鹏 1998 中国科学 43 1051 Google Scholar Yang J X, Yang X L, Chen G, Jiang K Y, Shen G T, Hu B Y, Jin R P 1998 Chin. Sci. Bull. 43 1051 Google Scholar
[10]	Gong W Y, Wu Z M, Lin H, Yang J X, Zhao Z J 2008 J. Magn. Magn. Mater. 320 1553 Google Scholar
[11]	方允樟, 许启明, 叶慧群, 郑金菊, 范晓珍, 潘日敏, 马云, 李文忠 2011 功能材料 42 1083 Fang Y Z, Xu Q M, Ye H Q, Zheng J J, Fan X Z, Pan R M, Ma Y, Li W Z 2011 Funct. Mater. 42 1083
[12]	Zhukov A, Ipatov M, Churyukanova M, Talaat A, Blanco J M, Zhukova V 2017 J. Alloys Compd. 727 887 Google Scholar
[13]	Herzer G 2013 Acta. Mater. 61 718 Google Scholar
[14]	Zhukov A, Ipatov M, Corte-Leon P, Gonzalez-Legarreta L, Churyukanova M, Blanco J M, Gonzalez J, Taskaev S, Hernando B, Zhukova V 2020 J. Alloys Compd. 814 152225 Google Scholar
[15]	Corte-Leon P, Zhukova V, Ipatov M, Blanco J M, Gonzalez J, Zhukov A 2019 Intermetallics 105 92 Google Scholar
[16]	Zhukova V, Blanco J M, Ipatov M, Gonzalez J, Churyukanova M, Zhukov A 2018 Scr. Mater. 142 10 Google Scholar
[17]	Phan M H, Peng H X 2008 Prog. Mater. Sci. 53 323 Google Scholar
[18]	Ohnuma M, Yanai T, Hono K, Nakano M, Fukunaga H, Yoshizawa Y, Herzer G 2010 J. Appl. Phys. 108 093927 Google Scholar
[19]	Kernion S J, Ohodnicki P R, Grossmann J J, Leary A, Shen S, Keylin V, Huth J F, Horwath J, Lucas M S, McHenry M E 2012 Appl. Phys. Lett. 101 102408 Google Scholar
[20]	Iannotti V, Amoruso S, Ausanio G, Wang X, Lanotte L, Barone A C, Margaris G, Trohidou K N, Fiorani D 2011 Phys. Rev. B 83 214422 Google Scholar
[21]	Bolyachkin A S, Volegov A S, Kudrevatykh N V 2015 J. Magn. Magn. Mater. 378 362 Google Scholar
[22]	Muscas G, Concas G, Laureti S, Testa A M, Mathieu R, De Toro J A, Cannas C, Musinu A, Novak M A, Sangregorio C, Lee S S, Peddis D 2018 Phys. Chem. Chem. Phys. 20 28634 Google Scholar
[23]	纪松, 杨国斌, 王润 1996 45 2061 Google Scholar Ji S, Yang G B, Wang R 1996 Acta Phys. Sin. 45 2061 Google Scholar
[24]	Hinokihara T, Miyashita S 2021 Phys. Rev. B 103 054421 Google Scholar
[25]	Hofmann B, Kronmüller H 1996 J. Magn. Magn. Mater. 152 91 Google Scholar
[26]	Herzer G 1995 Scr. Metall. Mater. 33 1741 Google Scholar
[27]	Hernando A, Kulik T 1994 Phys. Rev. B 49 7064 Google Scholar
[28]	张建强, 路飞平, 赵小龙, 何林芳 2019 磁性材料及器件 50 9 Zhang J Q, Lu F P, Zhao X L, He L F 2019 J. Magn. Mater. Device 50 9
[29]	Jaafar M, Pablo-Navarro A, Berganza E, Ares P, Magén C, Masseboeuf A, Gatel C, Snoeck E, Gómez-Herrero J, Teresa J M, Asenjo A 2020 Nanoscale 12 10090 Google Scholar

[1]	罗仕超, 吴里银, 常雨. 高超声速湍流流动磁流体动力学控制机理. , 2022, 71(21): 214702. doi: 10.7498/aps.71.20220941
[2]	邵先亦, 徐爱娇, 王天乐. 外磁场与带轴夹角对非晶FeSiB/Cu/FeSiB三明治薄带巨磁阻抗特性的影响. , 2019, 68(6): 067501. doi: 10.7498/aps.68.20181806
[3]	董博闻, 张静言, 彭丽聪, 何敏, 张颖, 赵云驰, 王超, 孙阳, 蔡建旺, 王文洪, 魏红祥, 沈保根, 姜勇, 王守国. 磁性斯格明子的多场调控研究. , 2018, 67(13): 137507. doi: 10.7498/aps.67.20180931
[4]	张树玲, 陈炜晔, 张勇. Co基金属纤维不对称巨磁阻抗效应. , 2015, 64(16): 167501. doi: 10.7498/aps.64.167501
[5]	张志东. 磁性材料的磁结构、磁畴结构和拓扑磁结构. , 2015, 64(6): 067503. doi: 10.7498/aps.64.067503
[6]	李印峰, 封素芹, 王建勇. 交流电流对铁基纳米晶丝巨磁阻抗效应形貌的影响. , 2011, 60(3): 037306. doi: 10.7498/aps.60.037306
[7]	方允樟, 许启明, 郑金菊, 吕葆华, 潘日敏, 叶慧群, 郑建龙, 范晓珍. FeCo基磁芯螺线管巨磁阻抗效应与磁芯长度关系的研究. , 2011, 60(12): 127501. doi: 10.7498/aps.60.127501
[8]	张树玲, 孙剑飞, 邢大伟. 磁场退火对Co基熔体抽拉丝巨磁阻抗效应的影响. , 2010, 59(3): 2068-2072. doi: 10.7498/aps.59.2068
[9]	潘海林, 程金科, 赵振杰, 何家康, 阮建中, 杨燮龙, 袁望治. LC共振型巨磁阻抗效应的研究. , 2008, 57(5): 3230-3236. doi: 10.7498/aps.57.3230
[10]	庞浩, 李根, 王赞基. 磁环中非晶丝的阻抗效应分析. , 2008, 57(11): 7194-7199. doi: 10.7498/aps.57.7194
[11]	辛宏梁, 袁望治, 程金科, 林宏, 阮建中, 赵振杰. NiFeCoP/BeCu复合结构丝的巨磁阻抗效应和磁化频率特性. , 2007, 56(7): 4152-4157. doi: 10.7498/aps.56.4152
[12]	王文静, 袁慧敏, 姜山, 萧淑琴, 颜世申. FeCuCrVSiB单层和多层膜的横向巨磁阻抗效应. , 2006, 55(11): 6108-6112. doi: 10.7498/aps.55.6108
[13]	刘龙平, 赵振杰, 黄灿星, 吴志明, 杨燮龙. 复合结构丝中的电流密度分布和巨磁阻抗效应. , 2006, 55(4): 2014-2020. doi: 10.7498/aps.55.2014
[14]	王文静, 萧淑琴, 刘宜华, 陈卫平, 代由勇, 姜山, 袁慧敏, 颜世申. 射频溅射功率对FeZrBCu软磁合金薄膜巨磁阻抗效应的影响. , 2005, 54(4): 1821-1825. doi: 10.7498/aps.54.1821
[15]	陈卫平, 萧淑琴, 王文静, 姜山, 刘宜华. FeCuCrVSiB多层膜巨磁阻抗效应的研究. , 2005, 54(6): 2929-2933. doi: 10.7498/aps.54.2929
[16]	杨全民, 王玲玲, 孙德成. 介观结构对纳米晶软磁合金巨磁阻抗效应影响的理论分析. , 2005, 54(12): 5730-5737. doi: 10.7498/aps.54.5730
[17]	王艾玲, 刘江涛, 周云松, 姜宏伟, 郑　鹉. 各向异性场对三明治膜巨磁阻抗效应的影响. , 2004, 53(3): 905-910. doi: 10.7498/aps.53.905
[18]	刘江涛, 周云松, 王艾玲, 姜宏伟, 郑鹉. 三明治结构与同轴电缆结构磁性材料巨磁阻抗效应的理论研究. , 2003, 52(11): 2859-2864. doi: 10.7498/aps.52.2859
[19]	钟智勇, 兰中文, 张怀武, 刘颖力, 王豪才. 铁磁/非铁磁/铁磁层状薄膜的巨磁阻抗效应的计算. , 2001, 50(8): 1610-1615. doi: 10.7498/aps.50.1610
[20]	萧淑琴, 刘宜华, 颜世申, 代由勇, 张林, 梅良模. FeCuNbSiB单层膜和三明治膜的磁特性与巨磁阻抗效应. , 1999, 48(13): 187-192. doi: 10.7498/aps.48.187

计量

文章访问数: 3525
PDF下载量: 45
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板