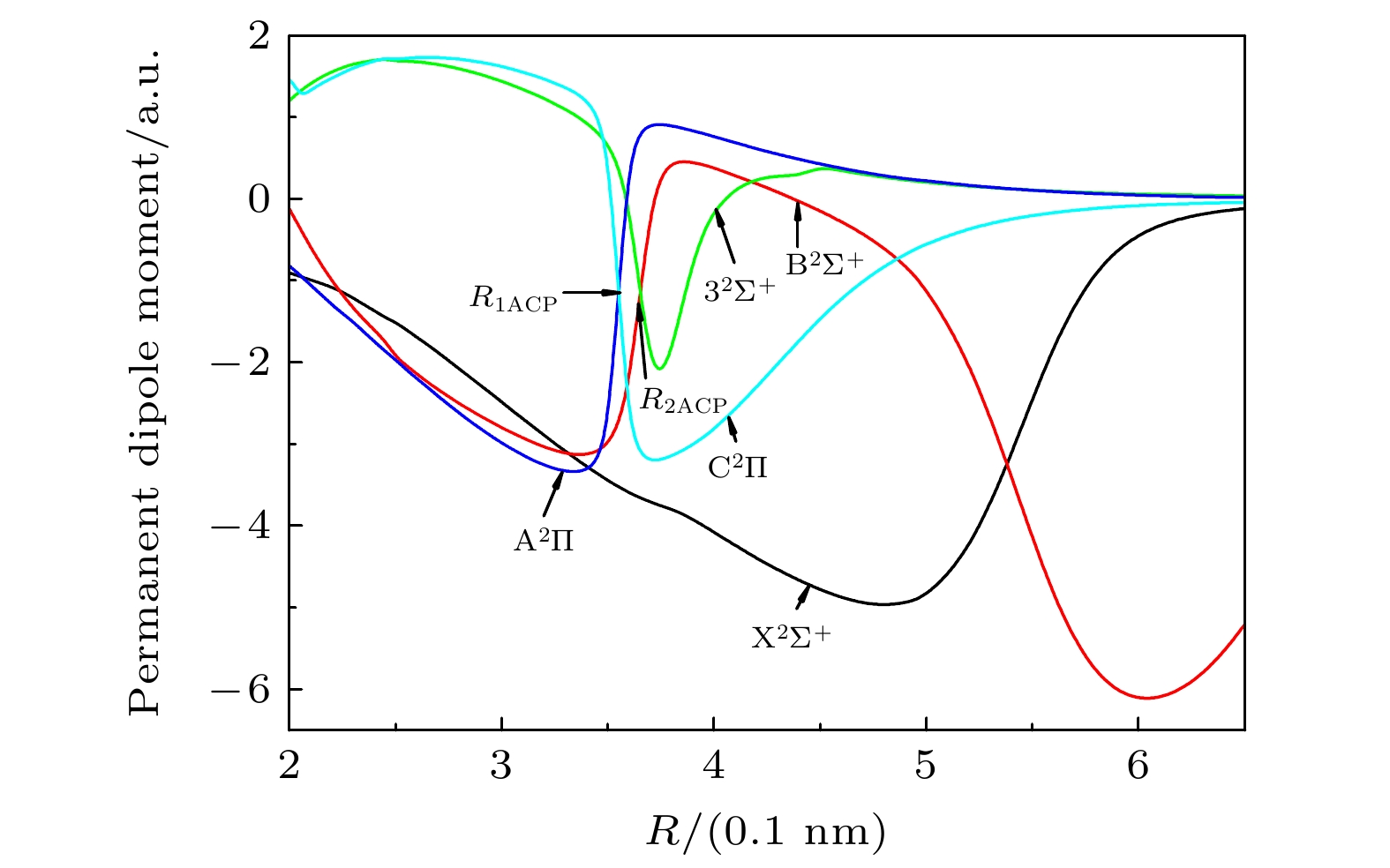
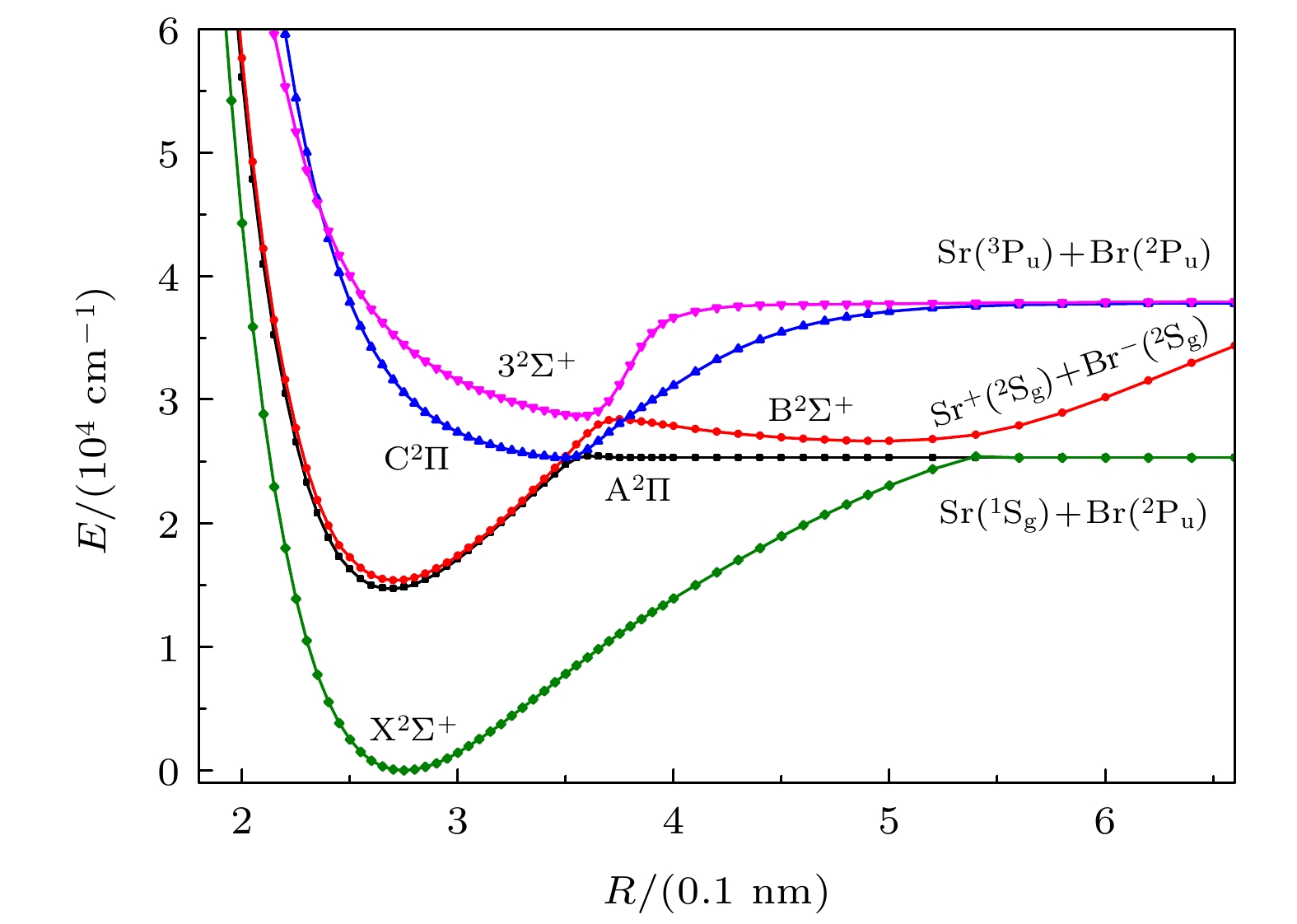
-
采用内收缩多参考组态相互作用(ic-MRCI)方法和相对论有效芯赝势基(aug-cc-pV5Z-PP), 优化计算一溴化锶(88Sr79Br)分子14个低激发电子态的电子结构和单点能. 为了获得更加精确的光谱参数, 引入Davidson、核价电子相关和相对论效应修正单点能, 根据优化修正得到的单点能分析获得了最低5个束缚态的势能曲线和偶极矩. 利用LEVEL8.0程序拟合修正的势能曲线, 得到各束缚态的光谱常数、分子常数和振动能级等光谱性质参数. 对比发现本文计算的结果与实验值吻合较好, 最后给出了跃迁性质参数Franck-Condon因子和辐射寿命. 这些光谱特性参数为进一步实验测量和构建分子激光冷却方案提供理论支持.
-
关键词:
- 88Sr79Br分子 /
- ic-MRCI /
- 光谱和分子常数 /
- 振动能级
The electronic structures and single point energy of 14 lowest electronic states of 88Sr79Br molecule are optimized by using the internal contraction multi-reference configuration interaction method and relativistic effective core pseudo-potential basis. Because 88Sr79Br molecule belongs to heavy element system, the single point energy must be corrected to obtain more accurate spectral parameters. Therefore, Davidson is introduced to correct the energy inconsistency, nuclear valence correlation is used to correct the electron correlation effect of inner shell and valence shell, and the relativistic scalar effect is corrected by calculating the third-order Douglas-Kroll-Hess Hamilton single electron integral. According to the single point energy calculated by the modified optimization, the potential energy curves, electric dipole moments, and transition dipole moments of 14 lowest electronic states are obtained. Using the latest LEVEL8.0 program to fit the modified potential energy curve, the spectral constants, molecular constants and vibration energy levels of 5 lowest bound states of 88Sr79Br molecule are given. In order to explain the changing trend of spectral constants of homologous compounds, the spectral parameters of each compound are compared and analyzed in this paper. At the same time, the vibration energy levels and molecular constants of 88Sr81Br molecule are also fitted and calculated for analyzing the influence of isotopes. The comparative analysis shows that the results of 88Sr79Br molecule are in better agreement with the experimental values. Finally, the Franck-Condon factors are gained by fitting the optimized single point energy and transition dipole moment of 88Sr79Br molecule. The transition band with the largest factor and obvious diagonalization is selected by analyzing the Franck-Condon factor of each transition band, and whether it meets the conditions for selecting laser cooling molecular system is judged. The radiation lifetimes of the transitions from the lowest two excited states to the ground state are calculated by combining the transition dipole moment, Franck-Condon factor, single point energy and vibration energy level of each electronic state. The results of this paper are in good agreement with the experimental values, which shows that the method in this paper is reliable. These spectral characteristic parameters provide theoretical support for further experimental measurement and construction of molecular laser cooling scheme of 88Sr79Br molecule.-
Keywords:
- 88Sr79Br molecule /
- ic-MRCI /
- spectroscopic and molecular constant /
- vibration levels
[1] Yang C L, Zhang X Y, Gao F, Ren T Q 2007 J. Mol. Struct. THEOCHEM 807 147
Google Scholar
[2] Wang C, Li N, Xia Y, Zhang X, Ge M, Liu Y, Li Q 2011 Comput. Theor. Chem. 963 319
Google Scholar
[3] Short C I, Hauschildt P H 2006 Astrophys. J. 641 494
Google Scholar
[4] Carlson K D, Claydon C R 1967 Adv. High Temp. Chem. 1 43
Google Scholar
[5] Hansen C J, Bergemann M, Cescutti G, Francois P, Arcones A, Karakas A I, Lind K, Chiappini C 2013 Astron. Astrophys. 551 1
Google Scholar
[6] Bergemann M, Hansen C J, Bautista M, Ruchti G 2012 Astron. Astrophys. 546 1
Google Scholar
[7] Caffau E, Andrievsky S, Korotin S, Origlia L, Oliva E, Sanna N, Ludwig H G, Bonifacio P 2016 Astron. Astrophys. 585 44
Google Scholar
[8] Törring T, Doebl K, Weiler G 1985 Chem. Phys. Lett. 117 539
Google Scholar
[9] Ernst W E, Schröder J O 1986 Z. Phys. D:At. Mol. Clusters 1 103
Google Scholar
[10] Keijzer F, Teule J M, Bulthuis J, de Graaff G J, Hilgeman M H, Janssen M H M, van Kleef E H, van Leuken J J, Stolte S 1996 Chem. Phys. 207 261
Google Scholar
[11] Coxon J A, Dickinson C S 1998 J. Mol. Spectrosc. 190 150
Google Scholar
[12] Gurvich L V, Ryabova V G, Khitrov A N 1973 Faraday Symp. Chem. Soc. 8 83
Google Scholar
[13] Hildenbrand D L 1977 J. Chem. Phys. 66 3526
Google Scholar
[14] Ernst W E, Schröder J O 1986 J. Mol. Spectrosc. 117 444
Google Scholar
[15] Dickinson C S, Coxon J A 2003 J. Mol. Spectrosc. 221 269
Google Scholar
[16] Schröder J O, Ernst W E 1985 J. Mol. Spectrosc. 112 413
Google Scholar
[17] Castano F, Sanchez Rayo M N, Pereira R, Adams J W, Husain D, Schifino J 1994 J. Photochem. Photobiol. , A 83 79
Google Scholar
[18] Gunduz S, Akman S 2014 Microchem. J. 116 1
Google Scholar
[19] Werner H J, Knowles P J, Knizia G, et al. 2012 MOLPRO, version 2012.1, a package of ab initio Programs
[20] Peterson K A, Figgen D, Goll E, Stoll H, Dolg M 2003 J. Chem. Phys. 119 11099
Google Scholar
[21] Werner H-J, Knowles P J 1985 J. Chem. Phys. 82 5053
Google Scholar
[22] Knowles P J, Werner H-J 1985 Chem. Phys. Lett. 115 259
Google Scholar
[23] Werner H-J, Knowles P J 1988 J. Chem. Phys. 89 5803
Google Scholar
[24] Knowles P J, Werner H-J 1988 Chem. Phys. Lett. 145 514
Google Scholar
[25] Le Roy R J 2007 LEVEL 8.0: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasi-bound Levels (Waterloo: University of Waterloo) Chemical Physics Research Report CP-663
[26] Wu D L, Tan B, Wen Y F, Zeng X F, Xie A D, Yan B 2016 Spectrochim. Acta, Part A 161 101
Google Scholar
[27] Fu M K, Ma H T, Cao J W, Bian W S 2017 J. Chem. Phys. 146 134309
Google Scholar
[28] Adema Z, Makhlouf S, Taher F 2016 Comput. Theor. Chem. 1093 48
Google Scholar
[29] Liu L, Yang C L, Wang M S, Ma X G, Sun Z P 2019 Spectrochim. Acta, Part A 164 162
Google Scholar
[30] Huber K P, Herzberg G 1979 Constants of Diatonic Molecules, Molecular spectra molecular structure (Vol. IV) (NewYork: Van Nostrand Reinhold)
[31] Wu D L, Lin C Q, Wen Y F, Xie A D, Yan B 2017 Chin. Phys. B 594 083101
Google Scholar
[32] 魏长立, 梁桂颖, 刘晓婷, 颜培源, 闫冰 2016 65 163101
Google Scholar
Wei C L, Liang G Y, Liu X T, Yan P Y, Yan B 2016 Acta. Phys. Sin. 65 163101
Google Scholar
[33] Zhang X M, Liang G Y, Li R, Shi D D, Liu Y C, Liu X S, Xu H F, Yan B 2014 Chem. Phys. 443 142
Google Scholar
[34] Okabe H 1978 Photochemistry of Small Molecules (New York: Wiley-Interscience)
[35] Zou W L, Liu W J 2005 J. Comput. Chem. 26 106
Google Scholar
[36] Bahrini C, Augé-Rochereau F, Rostas J, Taïeb G 2006 Chem. Phys. 330 130
Google Scholar
-
图 1 88Sr79Br分子5个激发态的势能曲线
Fig. 1. The potential energy curves of 5 lowest electronic states of 88Sr79Br.
图 2 88Sr79Br分子5个束缚态的电偶极矩
Fig. 2. The permanent dipole moments of 5 lowest electronic states of 88Sr79Br.
图 3 88Sr79Br分子5个束缚态的跃迁偶极矩
Fig. 3. The transition dipole moments of 5 bound states of 88Sr79Br.
表 1 5个束缚态的光谱常数
Table 1. The spectroscopic constants of the 5 lowest electronic states.
Λ-S 态 Te/cm–1 Re/nm ωe/cm–1 ωeχe/cm–1 Be/cm–1 αe/(10–4 cm–1) De/eV Re附近主要电子组态/% X2Σ+ 0.0 0.2740 216.17 0.499 0.0538 1.731 3.310 11σ212σα13σ06π47π2(80.2)
11σ212σ013σα6π47π2(6.9)理论[28] 0.0 0.2746 212.78 0.509 0.0535 — — 理论[29] 0.0 0.2799 205.6 0.53 0.051 1.742 — 实验[30] 0.0 0.2735 216 0.51 0.0541 — — A2Π 14679.348 0.2701 222.38 0.5346 0.0549 1.213 1.334 11σ212σ013σ06π47π3(86.1) 理论[28] 14657 0.272 220 0.57 0.0544 — — 理论[29] 14269.9 0.275 215.1 0.54 0.052 1.241 — 实验[30] 14850 0.2717 222 0.53 0.0545 — — B2Σ+ 15376.803 0.2702 223.03 0.5272 0.0552 1.799 1.597 11σ212σ013σα6π47π2(79.2)
11σ212σα13σ06π47π2(6.1)理论[28] 15208 0.2710 220.5 0.52 0.0547 — — 理论[29] 15222.8 0.2749 214.5 0.56 0.053 1.831 — 实验[30] 15352 0.2701 222 0.53 0.0552 — — C2Π 24947.818 0.3373 201.07 0.5012 0.0515 2.369 1.500
11σ212σ213σ06π37π3(80.0)
11σ212σ013σ06π47π3(2.2)
11σ212σ013σ06π37π4(2.8)
11σα12σα13σ06π47π3(2.7)理论[28] 25491 0.2810 197 0.49 0.0509 — — 理论[29] 25323.2 0.285 191.2 0.46 0.049 2.477 — 实验[30] 24665 — 205 0.49 — — — 32Σ+ 29079.756 0.3548 238.98 0.4556 0.0542 1.653 1.109 11σ212σα13σ06π47π2(1.3)
11σα12σ213σ06π47π2(69.4)
11σ212σ013σα6π47π2(5.3)
11σ212σα13σ06π37π3(2.9)
11σ212σ013σα6π47π1(.9)理论[28] 28117 0.266 242 0.54 0.0567 — — 理论[29] 27228.9 0.27 235.8 0.54 0.055 1.660 — 实验[30] 28958 — 247 0.55 — — — 
下载: 导出CSV
表 2 88Sr79Br分子5个束缚态的Gν, Bν和Dν值
Table 2. The values of Gν, Bν and Dν of 5 lowest electronic states for 88Sr79Br molecule.
ν 0 1 2 3 4 5 6 7 8 9 X2Σ+ Gν/cm–1 0 217.21 422.31 648.92 863.52 1077.13 1289.84 1501.60 1712.39 1922.24 Bν/cm–1 0.054170 0.054003 0.053836 0.053663 0.053494 0.053330 0.053165 0.052997 0.052827 0.052659 Dν/(10–8 cm–1) 1.299301 1.303053 1.284638 1.297713 1.299115 1.295311 1.296435 1.298790 1.296092 1.292529 A2Π Gν/cm–1 14691.87 14934.23 15175.25 15415.96 15656.46 15896.12 16134.07 16369.73 16603.1 16834.89 Bν/cm–1 0.055780 0.055620 0.055462 0.055295 0.055124 0.054976 0.054861 0.054772 0.054687 0.054578 Dν/(10–8 cm–1) 1.347703 1.355108 1.331605 1.313371 1.331860 1.390480 1.454430 1.476056 1.452901 1.372534 B2Σ+ Gν/cm–1 15376.52 15507.84 15738.33 15967.89 16196.74 16425.06 16652.61 16878.97 17103.8 17327.04 Bν/cm–1 0.055152 0.054998 0.054842 0.054679 0.054501 0.054326 0.054170 0.054020 0.053860 0.053722 Dν/(10–8 cm–1) 1.383536 1.380925 1.382206 1.370045 1.352258 1.361286 1.370500 1.430538 1.454700 1.453644 C2Π Gν/cm–1 25067.11 25478.29 25768.5 25995.01 26202.12 26394.03 26575.33 26748.69 26915.65 27077.76 Bν/cm–1 0.051613 0.051929 0.052694 0.053118 0.0536173 0.053991 0.054389 0.054762 0.055104 0.055412 Dν/(10–8 cm–1) 7.342555 2.052993 4.137982 4.629906 5.880088 6.862856 7.6697626 8.6153136 9.298999 9.430722 32Σ+ Gν/cm–1 31178.79 31534.74 31825.03 32085.24 32324.03 32546.51 32756.77 32958.15 33153 33342.76 Bν/cm–1 0.052457 0.052986 0.053498 0.053999 0.054484 0.054959 0.055414 0.055843 0.056246 0.056634 Dν/(10–8 cm–1) 8.487942 1.681584 2.237826 2.904620 3.611947 4.250499 4.782100 5.233730 5.676720 6.069434
下载: 导出CSV
表 3 88Sr79Br分子A2Π–X2Σ+和B2Σ+–X2Σ+跃迁的Franck-Condon因子
Table 3. The Franck-Condon factors of the transitions A2Π–X2Σ+和B2Σ+–X2Σ+ of 88Sr79Br.
ν'' = 0 1 2 3 4 5 6 7 8 9 A2Π–X2Σ+ ν' = 0 0.645022 0.336688 0.098008 0.017772 0.002264 0.000225 0.000019 0.000001 0.000000 0.000000 1 0.436688 0.083076 0.303189 0.190372 0.661533 0.165378 0.003316 0.000568 0.000087 0.000011 2 0.098008 0.434973 0.000835 0.180970 0.223953 0.113214 0.036827 0.009054 0.001812 0.000305 3 0.017772 0.293991 0.318827 0.055875 0.070256 0.256239 0.170741 0.062531 0.018499 0.004301 4 0.002263 0.053921 0.247678 0.100225 0.125148 0.010981 0.177146 0.190350 0.089728 0.031718 5 0.000225 0.009392 0.099735 0.271659 0.024898 0.160484 0.001473 0.098532 0.170079 0.114744 6 0.000019 0.001159 0.022742 0.145408 0.236122 0.000076 0.155129 0.024834 0.046417 0.151117 7 0.000000 0.000110 0.003473 0.042832 0.181875 0.178132 0.014614 0.150355 0.062132 0.011646 8 0.000000 0.000008 0.000391 0.008050 0.068736 0.202633 0.095379 0.050504 0.073401 0.096387 9 0.000000 0.000000 0.000034 0.001075 0.015763 0.098088 0.204697 0.042685 0.089124 0.031198 B2Σ+–X2Σ+ ν' = 0 0.825605 0.238234 0.033347 0.002666 0.000142 0.000006 0.000000 0.000000 0.000000 0.000000 1 0.388234 0.634880 0.110814 0.094271 0.088490 0.062873 0.040384 0.000047 0.000006 0.000000 2 0.033347 0.414395 0.520552 0.090304 0.084878 0.077853 0.067309 0.051175 0.000165 0.000020 3 0.002666 0.083449 0.366773 0.423286 0.082800 0.072301 0.061320 0.014268 0.002657 0.000419 4 0.000142 0.009678 0.107691 0.317402 0.350042 0.097638 0.0602219 0.055584 0.023573 0.005001 5 0.000006 0.000654 0.052162 0.087692 0.280018 0.317641 0.083112 0.07925 0.068340 0.044978 6 0.000000 0.000000 0.000117 0.006341 0.098918 0.277382 0.309402 0.081296 0.063711 0.051334 7 0.000000 0.000000 0.000093 0.003861 0.057313 0.055610 0.245025 0.292709 0.036511 0.075513 8 0.000000 0.000000 0.000004 0.000245 0.007248 0.080579 0.069675 0.186559 0.227752 0.010265 9 0.000000 0.000000 0.000000 0.000012 0.000552 0.012263 0.036322 0.069989 0.121499 0.152774
下载: 导出CSV
表 4 88Sr79Br分子A2Π–X2Σ+和B2Σ+–X2Σ+跃迁的辐射寿命
Table 4. The radiative lifetimes of the transitions A2Π–X2Σ+ and B2Σ+–X2Σ+ of 88Sr79Br.
Transition Radiative lifetimes/ns ν′ = 0 ν′ = 1 ν′ = 2 A2Π–X2Σ+ 32.23 32.35 32.56 B2Σ+–X2Σ+ 40.93 40.95 41.22
下载: 导出CSV
-
[1] Yang C L, Zhang X Y, Gao F, Ren T Q 2007 J. Mol. Struct. THEOCHEM 807 147
Google Scholar
[2] Wang C, Li N, Xia Y, Zhang X, Ge M, Liu Y, Li Q 2011 Comput. Theor. Chem. 963 319
Google Scholar
[3] Short C I, Hauschildt P H 2006 Astrophys. J. 641 494
Google Scholar
[4] Carlson K D, Claydon C R 1967 Adv. High Temp. Chem. 1 43
Google Scholar
[5] Hansen C J, Bergemann M, Cescutti G, Francois P, Arcones A, Karakas A I, Lind K, Chiappini C 2013 Astron. Astrophys. 551 1
Google Scholar
[6] Bergemann M, Hansen C J, Bautista M, Ruchti G 2012 Astron. Astrophys. 546 1
Google Scholar
[7] Caffau E, Andrievsky S, Korotin S, Origlia L, Oliva E, Sanna N, Ludwig H G, Bonifacio P 2016 Astron. Astrophys. 585 44
Google Scholar
[8] Törring T, Doebl K, Weiler G 1985 Chem. Phys. Lett. 117 539
Google Scholar
[9] Ernst W E, Schröder J O 1986 Z. Phys. D:At. Mol. Clusters 1 103
Google Scholar
[10] Keijzer F, Teule J M, Bulthuis J, de Graaff G J, Hilgeman M H, Janssen M H M, van Kleef E H, van Leuken J J, Stolte S 1996 Chem. Phys. 207 261
Google Scholar
[11] Coxon J A, Dickinson C S 1998 J. Mol. Spectrosc. 190 150
Google Scholar
[12] Gurvich L V, Ryabova V G, Khitrov A N 1973 Faraday Symp. Chem. Soc. 8 83
Google Scholar
[13] Hildenbrand D L 1977 J. Chem. Phys. 66 3526
Google Scholar
[14] Ernst W E, Schröder J O 1986 J. Mol. Spectrosc. 117 444
Google Scholar
[15] Dickinson C S, Coxon J A 2003 J. Mol. Spectrosc. 221 269
Google Scholar
[16] Schröder J O, Ernst W E 1985 J. Mol. Spectrosc. 112 413
Google Scholar
[17] Castano F, Sanchez Rayo M N, Pereira R, Adams J W, Husain D, Schifino J 1994 J. Photochem. Photobiol. , A 83 79
Google Scholar
[18] Gunduz S, Akman S 2014 Microchem. J. 116 1
Google Scholar
[19] Werner H J, Knowles P J, Knizia G, et al. 2012 MOLPRO, version 2012.1, a package of ab initio Programs
[20] Peterson K A, Figgen D, Goll E, Stoll H, Dolg M 2003 J. Chem. Phys. 119 11099
Google Scholar
[21] Werner H-J, Knowles P J 1985 J. Chem. Phys. 82 5053
Google Scholar
[22] Knowles P J, Werner H-J 1985 Chem. Phys. Lett. 115 259
Google Scholar
[23] Werner H-J, Knowles P J 1988 J. Chem. Phys. 89 5803
Google Scholar
[24] Knowles P J, Werner H-J 1988 Chem. Phys. Lett. 145 514
Google Scholar
[25] Le Roy R J 2007 LEVEL 8.0: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasi-bound Levels (Waterloo: University of Waterloo) Chemical Physics Research Report CP-663
[26] Wu D L, Tan B, Wen Y F, Zeng X F, Xie A D, Yan B 2016 Spectrochim. Acta, Part A 161 101
Google Scholar
[27] Fu M K, Ma H T, Cao J W, Bian W S 2017 J. Chem. Phys. 146 134309
Google Scholar
[28] Adema Z, Makhlouf S, Taher F 2016 Comput. Theor. Chem. 1093 48
Google Scholar
[29] Liu L, Yang C L, Wang M S, Ma X G, Sun Z P 2019 Spectrochim. Acta, Part A 164 162
Google Scholar
[30] Huber K P, Herzberg G 1979 Constants of Diatonic Molecules, Molecular spectra molecular structure (Vol. IV) (NewYork: Van Nostrand Reinhold)
[31] Wu D L, Lin C Q, Wen Y F, Xie A D, Yan B 2017 Chin. Phys. B 594 083101
Google Scholar
[32] 魏长立, 梁桂颖, 刘晓婷, 颜培源, 闫冰 2016 65 163101
Google Scholar
Wei C L, Liang G Y, Liu X T, Yan P Y, Yan B 2016 Acta. Phys. Sin. 65 163101
Google Scholar
[33] Zhang X M, Liang G Y, Li R, Shi D D, Liu Y C, Liu X S, Xu H F, Yan B 2014 Chem. Phys. 443 142
Google Scholar
[34] Okabe H 1978 Photochemistry of Small Molecules (New York: Wiley-Interscience)
[35] Zou W L, Liu W J 2005 J. Comput. Chem. 26 106
Google Scholar
[36] Bahrini C, Augé-Rochereau F, Rostas J, Taïeb G 2006 Chem. Phys. 330 130
Google Scholar
下载:
计量
- 文章访问数: 3281
- PDF下载量: 51
- 被引次数: 0
