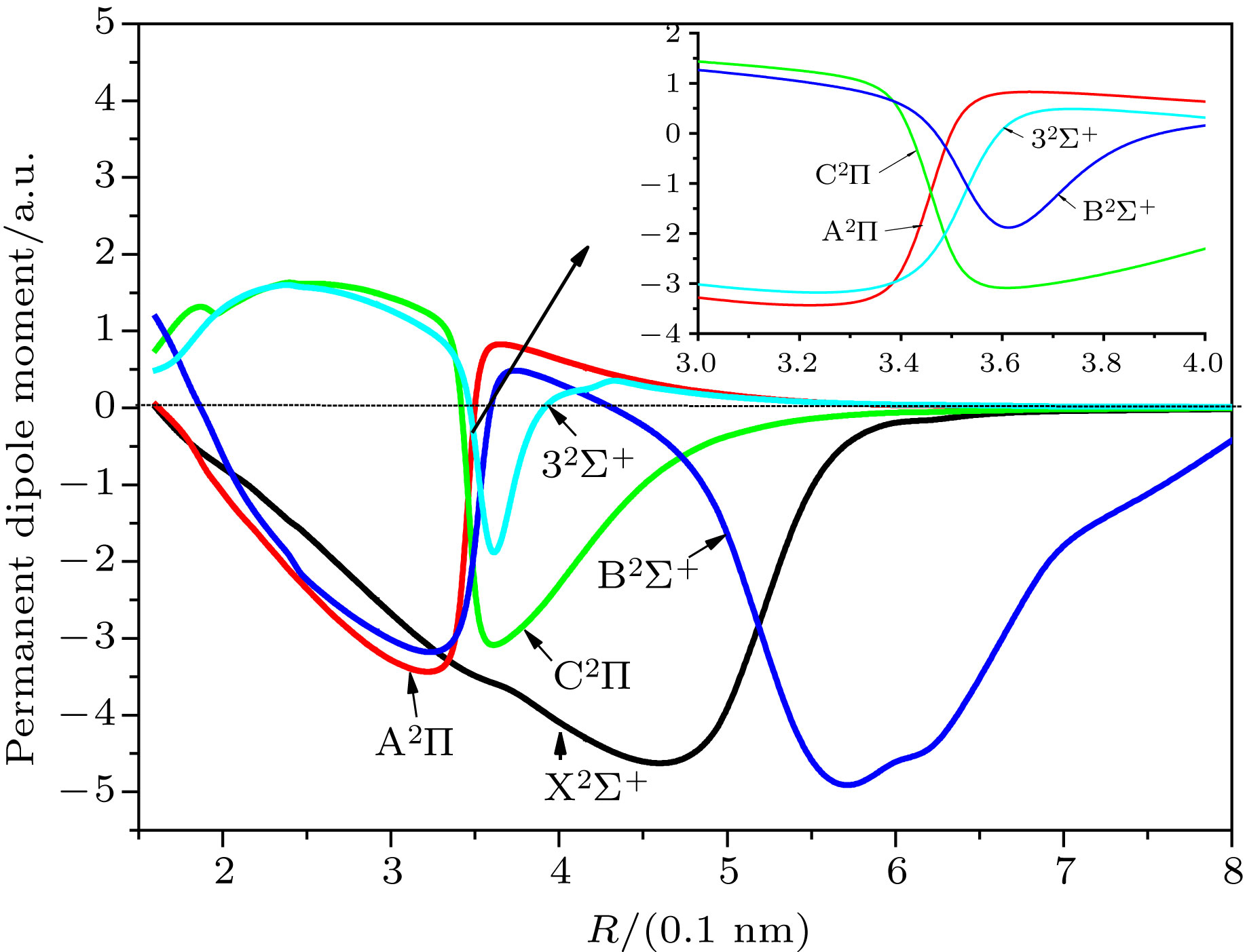
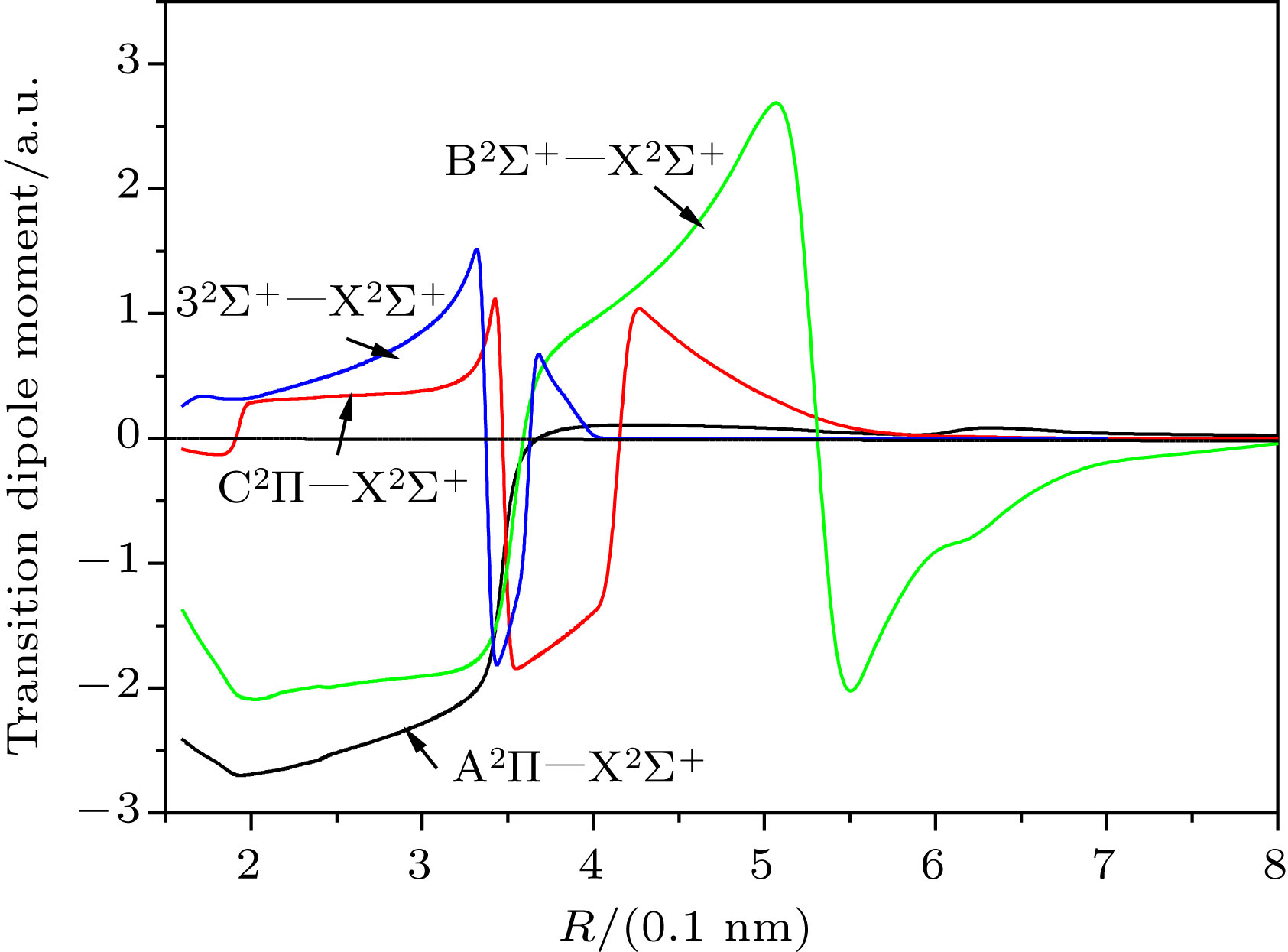
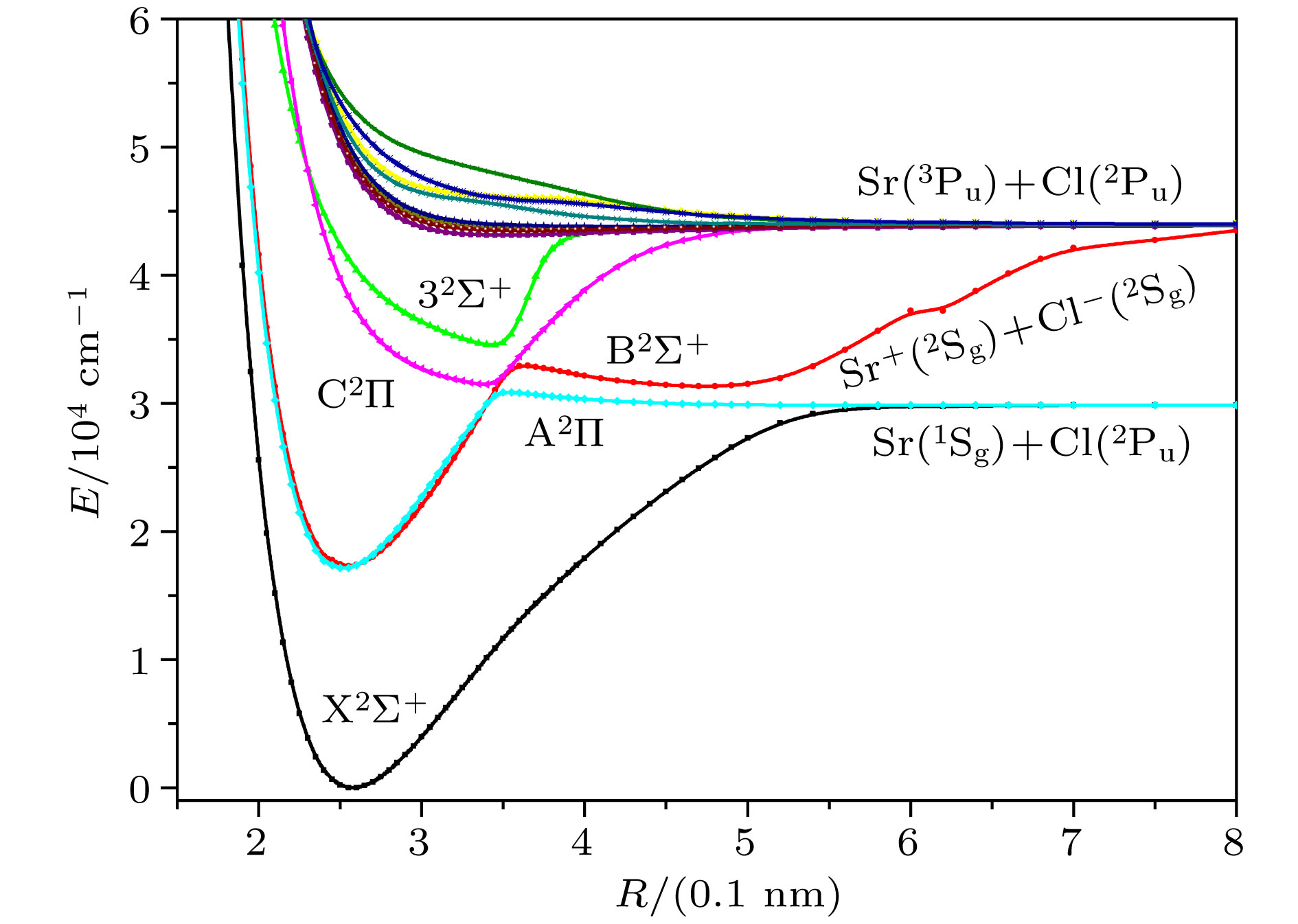
-
利用Davidson修正的内收缩多参考组态相互作用(ic-MRCI + Q)方法, 结合相对论有效芯赝势基(aug-cc-pV5Z-PP)作为Sr原子和相关一致五重基aug-cc-pV5Z为Cl原子的计算基组, 优化计算了单氯化锶(Sr35Cl)分子14个低激发电子态的势能曲线和跃迁偶极矩. 为了获得更加精确的光谱参数, 计算中同时引入核价电子相关和相对论效应修正势能曲线. 利用LEVEL 8.0程序拟合修正的势能曲线, 得到相应电子态的光谱常数、振动能级和分子常数等光谱性质, 结果与近来的已获得的理论计算和实验值符合得较好, 同时给出了Franck-Condon因子和辐射寿命等跃迁性质. 这些精确的光谱跃迁特性可为进一步构建Sr35Cl分子激光冷却方案提供理论支持.
-
关键词:
- Sr35Cl分子 /
- ic-MRCI + Q /
- 光谱和分子常数 /
- 振动能级 /
- 跃迁特性
Sr35Cl is a candidate system for laser cooling. The spectrum and transition characteristics are very important for constructing laser cooling schemes. In this paper, the spectral properties are analyzed by using the Davidson's modified internal contraction multi-reference interaction (ic-MRCI + Q) method, in combination with the relativistic effective core pseudopotential group (aug-cc-pV5Z-PP) as the base group for the calculation of the Sr atom and the related consistent quintile aug-cc-pV5Z as the Cl atom. The potential energy curves and dipole moments of 14 low excited electron states of Sr35Cl molecule are optimized. In order to obtain more accurate spectral parameters, nuclear valence electron correlation and relativistic effect correction are introduced into the calculation. Using the LEVEL 8.0 program to fit the modified potential energy curves of 5 bound states, the spectral properties such as spectral constants, vibration energy levels, and molecular constants of the corresponding electron states are obtained. The results show that there is a double potential well in${\rm B}^2 \Sigma^+$ state and the cross phenomena are avoided in${\rm A}^2 \Pi$ and${\rm C}^2 \Pi$ ,${\rm B}^2 \Sigma^+$ and$3^2 \Sigma^+$ respectively. The spectrum and molecular constants are in good agreement with the recently obtained theoretical calculations and experimental values except the adiabatic excitation energy. It may be due to the fact that the effect of the interaction of electronic states is taken into account. The transition properties such as Frank-Condon factor and radiation lifetime are also given. It can be seen that the 0-0 band of${\rm B}^2 \Sigma^+$ −${\rm X}^2 \Sigma^+$ transition has the largest Franck-Condon factor of 0.861288, and the diagonalization is obvious, which is the condition for laser cooling. The lifetime of${\rm B}^2 \Sigma^+$ −${\rm X}^2 \Sigma^+$ transition is 38.89 ns, which is in accordance with the experimental value 39.6 ns ± l.6 ns. These precise spectral transition characteristics may provide theoretical support for further constructing the laser cooling scheme of Sr35Cl molecule.-
Keywords:
- Sr35Cl molecule /
- internal contraction multi-reference interaction /
- spectroscopic and molecular constant /
- vibration levels /
- transition characteristics
[1] Micheli A, Brennen G, Zoller P 2006 Nat. Phys. 2 341
Google Scholar
[2] Baron J, Campbell W C, DeMille D, Doyle J M, Gabrielse G, Gurevich Y V, Hess P W, Hutzler N R, Kirilov E, Kozyryev I, O'Leary B R, Panda C D, Parsons M F, Petrik E S, Spaun B, Vutha A C, West A D 2014 Science 343 269
Google Scholar
[3] Krems R V 2008 Phys. Chem. Chem. Phys. 10 4079
Google Scholar
[4] Walters O H, Barratt S 1928 Proc. R. Soc. London Ser. A 118 120
Google Scholar
[5] Nakagawa J, Domaille P J, Steimle T C, Harris D O 1978 J. Mol. Spectrosc. 70 374
Google Scholar
[6] Dulick M, Bernath P F, Field R W 1980 Can. J. Phys. 58 703
Google Scholar
[7] Domaille P J, Steimle T C, Wong N B, Harris D O 1977 J. Mol. Spectrosc. 65 354
Google Scholar
[8] Berg L E, Klynning L, Martin H 1980 Phys. Scr. 21 173
Google Scholar
[9] Bernath P F, Field R W, Pinchemel B, Lefebvre Y, Schamps J 1981 J. Mol. Spectrosc. 88 175
Google Scholar
[10] Reisner D E, Bernath P F, Field R W 1981 J. Mol. Spectrosc. 89 107
Google Scholar
[11] Zare R N, Schmeltekopf A L, Harrop W J, Albritton D L 1973 J. Mol. Spectrosc. 46 37
Google Scholar
[12] Singh J, Nair K P R, Upadhya K N, Rai D K 1970 Opt. Pure Appl. 3 76
[13] Brinkmann U, Schmidt V H, Telle H 1982 Chern. Phys. 64 19
[14] Schiitze Pahlmann H V, Ryzlewicz C H, Hoeft J, Torring T 1982 Chern. Phys. Lett. 93 74
Google Scholar
[15] Ernst W E, Schröder J O 1984 J. Chem. Phys. 81 136
Google Scholar
[16] Schruder J O, Zeller B, Ernst W E 1988 J. Mol. Spectrosc. 127 255
Google Scholar
[17] Berg L E, Royen P, Weijnitz P 1990 Mol. Phys. 69 385
Google Scholar
[18] Werner H J, Knowles P J, Knizia G, et al. 2012 MOLPRO, Version 2012.1, A Package of ab initio Programs
[19] Peterson K A, Figgen D, Goll E, Stoll H, Dolg M 2003 J. Chem. Phys. 119 11099
Google Scholar
[20] Werner H J, Knowles P J 1985 J. Chem. Phys. 82 5053
Google Scholar
[21] Knowles P J, Werner H J 1985 Chem. Phys. Lett. 115 259
Google Scholar
[22] Werner H J, Knowles P J 1988 J. Chem. Phys. 89 5803
Google Scholar
[23] Knowles P J, Werner H J 1988 Chem Phys Lett. 145 514
Google Scholar
[24] Le Roy R J 2007 LEVEL 8.0: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasi-bound Levels (Waterloo: University of Waterloo) Chemical Physics Research Report CP-663
[25] Fu M K, Ma H T, Cao J W, Bian W S 2016 J. Chem. Phys. 144 184302
Google Scholar
[26] Adema Z, Makhlouf S, Taher F 2016 Comput. Theor. Chem. 1093 48
Google Scholar
[27] Huber K P, Herzberg G 1979 Constants of Diatonic Molecules, Molecular Spectra Molecular Structure (Vol. IV) (New York: Van Nostrand Reinhold)
[28] Lima J C B D, Ornellas F R 2013 J. Mol. Spectrosc. 283 22
Google Scholar
[29] Wu D L, Lin C Q , Wen Y F, Xie A D, Yan B 2018 Chin. Phys. B 27 083101
Google Scholar
[30] Wu D L, Tan B, Wen Y F, Zeng X F, Xie A D, Yan B 2016 Spectrochim Acta Part A 161 101
Google Scholar
[31] 魏长立, 梁桂颖, 刘晓婷, 颜培源, 闫冰 2016 65 163101
Google Scholar
Wei C L, Liang G Y, Liu X T, Yan P Y, Yan B 2016 Acta Phys. Sin. 65 163101
Google Scholar
[32] Zhang X M, Liang G Y, Li R, Shi D D, Liu Y C, Liu X S, Xu H F, Yan B 2014 Chem. Phys. 443 142
Google Scholar
[33] Okabe H 1978 Photochemistry of Small Molecules (New York: Wiley-Interscience)
[34] Zou W L, Liu W J 2005 J. Comput. Chem. 26 106
Google Scholar
[35] Paul J D, Howard W C, Richard N Z 1974 J. Chem. Phys. 60 2330
Google Scholar
-
图 1 Sr35Cl分子14个激发态的势能曲线
Fig. 1. Potential energy curves of 14 excited states of Sr35Cl.
图 3 Sr35Cl分子5个束缚态的跃迁偶极矩
Fig. 3. Transition dipole moments of 5 bound states of Sr35Cl.
表 1 5个束缚态的光谱常数
Table 1. Spectroscopic constants of the 5 bound states.
Λ-S态 Te/cm−1 Re/nm $\omega $e/cm−1 $\omega $e$\chi $e/cm−1 Be/cm−1 104αe/cm−1 De/eV Re附近主要电子组态(%) $ {{\rm{X}}^{2}}\Sigma^+$ 0.0 0.2575 309.78 0.8682 0.1016 4.131 3.703 6$\text{σ}$ 27$\text{σ}$ 28$\text{σ}$ α9$\text{σ}$ 03$\text{π}$24$\text{π}$2(78.8)
6${\rm{\sigma }}$ 27$\text{σ}$ 28$\text{σ}$ 09$\text{σ}$ α3$\text{π}$24$\text{π}$2(7.5)理论[26] 0.0 0.255 313 0.93 0.1037 — — 实验[15] 0.0 0.257 302[27] 0.95[27] — — — 实验[16] 0.0 — 302.448 −0.9502 0.1016 4.524 — 实验[12] 0.0 — 302.3 0.950 — — — $ {{\rm{A}}^{2}}\Pi$ 15779.16 0.2518 330.69 — 0.1061 2.013 1.673 6$\text{σ}$ 27$\text{σ}$ 28$\text{σ}$ 09$\text{σ}$ 03$\text{π}$ααβ 4$\text{π}$2(85.7) 理论[26] 14730 0.252 323 0.95 0.1055 — — 实验[15] 14818 0.255 309[27] 0.98[27] — — — 实验[16] 14966.727 — 309.625 0.996 0.1030 4.606 — $ {{\rm{B}}^{2}}\Sigma^+$ 16612.74 0.2538 318.67 0.4874 0.1043 2.599 1.937 6$\text{σ}$ 27$\text{σ}$ 28$\text{σ}$ α9$\text{σ}$ 03$\text{π}$24$\text{π}$2(78.8)
6${\rm{\sigma }}$ 27$\text{σ}$ 28$\text{σ}$ 09$\text{σ}$ α3$\text{π}$24$\text{π}$2(7.6)理论[26] 15714 0.253 319 0.99 0.1055 — — 实验[15] 15719 0.255 306[27] 0.98[27] 0.1030[16] — — 实验[12] 15719.5 — 306.4 0.98 — — — — $ {{\rm{C}}^{2}}\Pi$ 33532.99 0.3477 425.57 15.5691 0.0554 −11.932 1.546 6$\text{σ}$ 27$\text{σ}$ 28$\text{σ}$ 09$\text{σ}$ 03$\text{π}$ααβ 4$\text{π}$2(59.7)
6$\text{σ}$ 27$\text{σ}$ 28$\text{σ}$ 29$\text{σ}$ 03$\text{π}$24$\text{π}$2(13.4)
6$\text{σ}$ 27$\text{σ}$ α8$\text{σ}$ β9$\text{σ}$ 03$\text{π}$ααβ 4π2(9.8)
6$\text{σ}$ 27$\text{σ}$ α8$\text{σ}$ α9$\text{σ}$ 03$\text{π}$αββ 4$\text{π}$2(2.7)理论[26] 26688 0.259 278 0.83 0.1095 — — 实验[27] 26099 — 270 0.72 — — — $ {{\rm{3}}^{2}}\Sigma^+$ 36625.55 0.3519 392.49 10.4544 0.0544 −12.567 1.140 6$\text{σ}$ 27$\text{σ}$ α8$\text{σ}$ 29$\text{σ}$ 03$\text{π}$24$\text{π}$2(51.0)
6$\text{σ}$ 27$\text{σ}$ 28$\text{σ}$ 09$\text{σ}$ α3$\text{π}$24$\text{π}$2(16.4)
6$\text{σ}$ 27$\text{σ}$ 28$\text{σ}$ α9$\text{σ}$ 03$\text{π}$ααβ 4$\text{π}$2(4.6)
6$\text{σ}$ 27$\text{σ}$ 28$\text{σ}$ α9$\text{σ}$ 03$\text{π}$β4$\text{π}$ααβ (4.6)
6$\text{σ}$ 27$\text{σ}$ 28$\text{σ}$ α9$\text{σ}$ 03$\text{π}$24$\text{π}$2(2.5)
6$\text{σ}$ 27$\text{σ}$ 28$\text{σ}$ α9$\text{σ}$ 03$\text{π}$αββ 4$\text{π}$2(1.6)
6$\text{σ}$ 27$\text{σ}$ 28$\text{σ}$ 09$\text{σ}$ α3$\text{π}$α4$\text{π}$αββ (1.6)
6$\text{σ}$ 27$\text{σ}$ α8$\text{σ}$ 09$\text{σ}$ 03$\text{π}$44$\text{π}$2(1.5)
6$\text{σ}$ 27$\text{σ}$ α8$\text{σ}$ 09$\text{σ}$ 03$\text{π}$24$\text{π}$4(1.5)理论[26] 27979 0.248 358 1.01 0.1095 — — 实验[15] 28822 — 344[27] 1.04[27] 0.1030[16] — — 
下载: 导出CSV
表 2 Sr35Cl分子
$ {{\rm{X}}^{2}}\Sigma^+$ ,$ {{\rm{A}}^{2}}\Pi$ ,$ {{\rm{B}}^{2}}\Sigma^+$ ,$ {{\rm{C}}^{2}}\Pi$ 和$ {{\rm{3}}^{2}}\Sigma^+$ 的Gv, Bv和Dv值Table 2. The Gv, Bv and Dv of
$ {{\rm{X}}^{2}}\Sigma^+$ ,$ {{\rm{A}}^{2}}\Pi$ ,$ {{\rm{B}}^{2}}\Sigma^+$ ,$ {{\rm{C}}^{2}}\Pi$ and$ {{\rm{3}}^{2}}\Sigma^+$ states of Sr35Cl.v 0 1 2 3 4 5 6 7 8 9 $ {{\rm{X}}^{2}}\Sigma^+$ Gv/cm−1 0 308.69 615.44 919.34 1220.80 1520.91 1820.07 2118.05 2414.53 2709.33 Bv/cm−1 0.101389 0.100964 0.100567 0.100209 0.099815 0.099369 0.098910 0.098467 0.098043 0.097629 108Dv/cm−1 4.351839 4.364577 4.467493 4.497514 4.362226 4.242542 4.234360 4.286016 4.334124 4.353049 $ {{\rm{A}}^{2}}\Pi$ Gv/cm−1 15953.74 16281.83 16598.43 16930.62 17269.01 17605.65 17940.04 18272.59 18603.52 18933.04 Bv/cm−1 0.106234 0.106462 0.106095 0.105137 0.104604 0.104235 0.103859 0.103475 0.103082 0.102679 108Dv/cm−1 4.461909 5.111509 3.253476 3.332790 4.007870 4.130323 4.085546 4.040997 3.976138 3.938946 $ {{\rm{B}}^{2}}\Sigma^+$ Gv/cm−1 16777.58 17097.77 17402.46 17705.63 18020.44 18339.16 18656.69 18972.44 19286.60 19599.30 Bv/cm−1 0.104260 0.104168 0.104392 0.103697 0.102831 0.102297 0.101900 0.101515 0.101130 0.100741 108Dv/cm−1 4.416717 5.342062 4.947374 3.120903 3.500412 4.129428 4.273733 4.244199 4.206411 4.139361 $ {{\rm{C}}^{2}}\Pi$ Gv/cm−1 33822.25 34298.68 34607.21 34880.81 35124.57 35352.15 35566.01 35770.85 35971.25 36169.15 Bv/cm−1 0.056049 0.057354 0.058912 0.059995 0.060974 0.062071 0.063032 0.063843 0.064515 0.065071 108Dv/cm−1 0.293093 1.069720 1.371596 2.128287 2.433073 3.023576 3.386636 3.382563 3.426546 3.529599 $ {{\rm{3}}^{2}}\Sigma^+$ Gv/cm−1 36879.56 37294.02 37638.56 37944.07 38221.43 38480.16 38726.99 38965.82 39199.02 39428.18 Bv/cm−1 0.055079 0.056481 0.057758 0.059028 0.060242 0.061377 0.062432 0.063414 0.064332 0.065193 108Dv/cm−1 0.363052 0.690909 1.002658 1.373820 1.690530 1.922724 2.122355 2.300506 2.453955 2.583320
下载: 导出CSV
表 3 Sr35Cl分子
$ {{\rm{A}}^{2}}\Pi$ —$ {{\rm{X}}^{2}}\Sigma^+ $ ,$ {{\rm{B}}^{2}}\Sigma^+$ —$ {{\rm{X}}^{2}}\Sigma^+ $ ,$ {{\rm{C}}^{2}}\Pi$ —$ {{\rm{X}}^{2}}\Sigma^+ $ 和$ {{\rm{3}}^{2}}\Sigma^+$ —$ {{\rm{X}}^{2}}\Sigma^+ $ 跃迁的Franck-Condon因子Table 3. The Franck-Condon factors of the transitions
$ {{\rm{A}}^{2}}\Pi$ −$ {{\rm{X}}^{2}}\Sigma^+ $ ,$ {{\rm{B}}^{2}}\Sigma^+$ −$ {{\rm{X}}^{2}}\Sigma^+ $ ,$ {{\rm{C}}^{2}}\Pi$ −$ {{\rm{X}}^{2}}\Sigma^+ $ and$ {{\rm{3}}^{2}}\Sigma^+$ −$ {{\rm{X}}^{2}}\Sigma^+ $ .v′′ = 0 1 2 3 4 5 6 7 8 9 $ {{\rm{A}}^{2}}\Pi$—$ {{\rm{X}}^{2}}\Sigma^+ $ v′ = 0 0.656888 0.266608 0.062027 0.011563 0.002170 0.000520 0.000163 0.000048 0.000007 0.000000 1 0.272308 0.192420 0.320947 0.150685 0.466479 0.012567 0.033544 0.008655 0.000174 0.000137 2 0.061741 0.365100 0.012591 0.236003 0.200935 0.086356 0.027568 0.007557 0.001791 0.000312 3 0.008378 0.145153 0.330434 0.013476 0.132392 0.200767 0.112395 0.041433 0.012093 0.002903 4 0.000641 0.027499 0.211170 0.231162 0.064589 0.062086 0.184983 0.134977 0.058263 0.018761 5 0.000040 0.003015 0.053925 0.25428 0.132467 0.115528 0.018774 0.155878 0.151198 0.077211 6 0.000004 0.000182 0.008221 0.084623 0.271397 0.058393 0.151118 0.000803 0.117380 0.157174 7 0.000000 0.000021 0.006253 0.016398 0.117920 0.263055 0.014702 0.164939 0.005113 0.077068 8 0.000000 0.000000 0.000052 0.001674 0.027547 0.151418 0.233623 0.000068 0.157208 0.024940 9 0.000000 0.000000 0.000007 0.000118 0.003627 0.041888 0.181283 0.190225 0.008630 0.133109 $ {{\rm{B}}^{2}}\Sigma^+$—$ {{\rm{X}}^{2}}\Sigma^+ $ v′ = 0 0.861288 0.125494 0.011927 0.001065 0.000142 0.000047 0.000025 0.000091 0.000000 0.000000 1 0.129692 0.603795 0.220001 0.038332 0.006251 0.001365 0.000411 0.000120 0.000019 0.000000 2 0.008650 0.241321 0.360072 0.284163 0.081308 0.018646 0.004456 0.001109 0.000226 0.000018 3 0.000365 0.027661 0.352567 0.179385 0.288215 0.112584 0.030079 0.007227 0.001600 0.000265 4 0.000002 0.001707 0.051462 0.411903 0.083378 0.268533 0.131641 0.039281 0.009668 0.002055 5 0.000001 0.000017 0.003843 0.078423 0.421433 0.034730 0.246976 0.148790 0.049663 0.012870 6 0.000000 0.000000 0.000117 0.006341 0.108918 0.407382 0.009402 0.221296 0.163711 0.061334 7 8 0.000000 0.000000 0.000003 0.000002 0.000001 0.000007 0.000333 0.000002 0.009581 0.000763 0.141252 0.014168 0.381199 0.173321 0.000074 0.346687 0.190975 0.003801 0.174597 0.158106 9 0.000000 0.000000 0.000000 0.000000 0.000000 0.001272 0.020484 0.203605 0.306437 0.017104 $ {{\rm{C}}^{2}}\Pi$—$ {{\rm{X}}^{2}}\Sigma^+ $ v′ = 0 0.000002 0.000057 0.000400 0.002491 0.013257 0.048381 0.121107 0.211164 0.245963 0.199742 1 0.000028 0.000755 0.003923 0.016478 0.054711 0.112499 0.129055 0.063035 0.000478 0.054393 2 0.000216 0.004536 0.018057 0.052861 0.110648 0.119527 0.040456 0.002385 0.059184 0.058927 3 0.000894 0.014294 0.042688 0.083192 0.097065 0.033697 0.003920 0.060262 0.039865 0.000817 $ {{\rm{3}}^{2}}\Sigma^+$—$ {{\rm{X}}^{2}}\Sigma^+ $ v′ = 0 0.000005 0.000160 0.001014 0.005583 0.025973 0.082035 0.174625 0.263266 0.237744 0.147940 1 0.000072 0.001726 0.007985 0.028959 0.080861 0.133268 0.106890 0.018946 0.019348 0.137924 2 0.000444 0.008122 0.028147 0.068699 0.114064 0.085695 0.008341 0.025544 0.075168 0.024261 3 0.001887 0.025614 0.064048 0.096749 0.076464 0.007949 0.023664 0.062244 0.010184 0.021472 4 0.005823 0.057375 0.098715 0.079207 0.013459 0.015420 0.056215 0.010480 0.018687 0.044825 5 0.013104 0.091074 0.099009 0.027450 0.005603 0.051927 0.016773 0.012448 0.040966 0.001448 6 0.023467 0.109148 0.062336 0.000039 0.043234 0.033313 0.003366 0.042212 0.004752 0.023015 7 0.036552 0.106016 0.020316 0.019085 0.055807 0.001734 0.035028 0.017051 0.012699 0.031310 8 0.052050 0.085867 0.000431 0.051861 0.028088 0.011562 0.037256 0.000833 0.036176 0.001957 9 0.069548 0.057189 0.008529 0.060907 0.001791 0.038489 0.008713 0.024666 0.015229 0.013407
下载: 导出CSV
表 4 Sr35Cl分子
$ {{\rm{A}}^{2}}\Pi $ —$ {{\rm{X}}^{2}}\Sigma^+ $ ,$ {{\rm{B}}^{2}}\Sigma^+ $ —$ {{\rm{X}}^{2}}\Sigma^+ $ 和$ {{\rm{C}}^{2}}\Pi $ —$ {{\rm{X}}^{2}}\Sigma^+ $ 跃迁的辐射寿命Table 4. Radiative lifetimes of the transitions
$ {{\rm{A}}^{2}}\Pi $ −$ {{\rm{X}}^{2}}\Sigma^+ $ ,$ {{\rm{B}}^{2}}\Sigma^+ $ −$ {{\rm{X}}^{2}}\Sigma^+ $ and$ {{\rm{C}}^{2}}\Pi $ −$ {{\rm{X}}^{2}}\Sigma^+ $ .Transition Radiative lifetimes/ns v′ = 0 v′ = 1 v′ = 2 $ {{\rm{A}}^{2}}\Pi $—$ {{\rm{X}}^{2}}\Sigma^+ $ 31.23 31.35 31.56 $ {{\rm{B}}^{2}}\Pi $—$ {{\rm{X}}^{2}}\Sigma^+ $ 38.83 38.89 39.12 $ {{\rm{C}}^{2}}\Pi$—$ {{\rm{X}}^{2}}\Sigma^+ $ 25.92 26.01 26.18
下载: 导出CSV
-
[1] Micheli A, Brennen G, Zoller P 2006 Nat. Phys. 2 341
Google Scholar
[2] Baron J, Campbell W C, DeMille D, Doyle J M, Gabrielse G, Gurevich Y V, Hess P W, Hutzler N R, Kirilov E, Kozyryev I, O'Leary B R, Panda C D, Parsons M F, Petrik E S, Spaun B, Vutha A C, West A D 2014 Science 343 269
Google Scholar
[3] Krems R V 2008 Phys. Chem. Chem. Phys. 10 4079
Google Scholar
[4] Walters O H, Barratt S 1928 Proc. R. Soc. London Ser. A 118 120
Google Scholar
[5] Nakagawa J, Domaille P J, Steimle T C, Harris D O 1978 J. Mol. Spectrosc. 70 374
Google Scholar
[6] Dulick M, Bernath P F, Field R W 1980 Can. J. Phys. 58 703
Google Scholar
[7] Domaille P J, Steimle T C, Wong N B, Harris D O 1977 J. Mol. Spectrosc. 65 354
Google Scholar
[8] Berg L E, Klynning L, Martin H 1980 Phys. Scr. 21 173
Google Scholar
[9] Bernath P F, Field R W, Pinchemel B, Lefebvre Y, Schamps J 1981 J. Mol. Spectrosc. 88 175
Google Scholar
[10] Reisner D E, Bernath P F, Field R W 1981 J. Mol. Spectrosc. 89 107
Google Scholar
[11] Zare R N, Schmeltekopf A L, Harrop W J, Albritton D L 1973 J. Mol. Spectrosc. 46 37
Google Scholar
[12] Singh J, Nair K P R, Upadhya K N, Rai D K 1970 Opt. Pure Appl. 3 76
[13] Brinkmann U, Schmidt V H, Telle H 1982 Chern. Phys. 64 19
[14] Schiitze Pahlmann H V, Ryzlewicz C H, Hoeft J, Torring T 1982 Chern. Phys. Lett. 93 74
Google Scholar
[15] Ernst W E, Schröder J O 1984 J. Chem. Phys. 81 136
Google Scholar
[16] Schruder J O, Zeller B, Ernst W E 1988 J. Mol. Spectrosc. 127 255
Google Scholar
[17] Berg L E, Royen P, Weijnitz P 1990 Mol. Phys. 69 385
Google Scholar
[18] Werner H J, Knowles P J, Knizia G, et al. 2012 MOLPRO, Version 2012.1, A Package of ab initio Programs
[19] Peterson K A, Figgen D, Goll E, Stoll H, Dolg M 2003 J. Chem. Phys. 119 11099
Google Scholar
[20] Werner H J, Knowles P J 1985 J. Chem. Phys. 82 5053
Google Scholar
[21] Knowles P J, Werner H J 1985 Chem. Phys. Lett. 115 259
Google Scholar
[22] Werner H J, Knowles P J 1988 J. Chem. Phys. 89 5803
Google Scholar
[23] Knowles P J, Werner H J 1988 Chem Phys Lett. 145 514
Google Scholar
[24] Le Roy R J 2007 LEVEL 8.0: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasi-bound Levels (Waterloo: University of Waterloo) Chemical Physics Research Report CP-663
[25] Fu M K, Ma H T, Cao J W, Bian W S 2016 J. Chem. Phys. 144 184302
Google Scholar
[26] Adema Z, Makhlouf S, Taher F 2016 Comput. Theor. Chem. 1093 48
Google Scholar
[27] Huber K P, Herzberg G 1979 Constants of Diatonic Molecules, Molecular Spectra Molecular Structure (Vol. IV) (New York: Van Nostrand Reinhold)
[28] Lima J C B D, Ornellas F R 2013 J. Mol. Spectrosc. 283 22
Google Scholar
[29] Wu D L, Lin C Q , Wen Y F, Xie A D, Yan B 2018 Chin. Phys. B 27 083101
Google Scholar
[30] Wu D L, Tan B, Wen Y F, Zeng X F, Xie A D, Yan B 2016 Spectrochim Acta Part A 161 101
Google Scholar
[31] 魏长立, 梁桂颖, 刘晓婷, 颜培源, 闫冰 2016 65 163101
Google Scholar
Wei C L, Liang G Y, Liu X T, Yan P Y, Yan B 2016 Acta Phys. Sin. 65 163101
Google Scholar
[32] Zhang X M, Liang G Y, Li R, Shi D D, Liu Y C, Liu X S, Xu H F, Yan B 2014 Chem. Phys. 443 142
Google Scholar
[33] Okabe H 1978 Photochemistry of Small Molecules (New York: Wiley-Interscience)
[34] Zou W L, Liu W J 2005 J. Comput. Chem. 26 106
Google Scholar
[35] Paul J D, Howard W C, Richard N Z 1974 J. Chem. Phys. 60 2330
Google Scholar
下载:
计量
- 文章访问数: 7188
- PDF下载量: 53
- 被引次数: 0
