-
神经元的大小属于介观尺度范围, 本文考虑神经元的电感特性, 建立了由细胞膜电感、膜电容、钾离子忆阻器和氯离子电阻构成的神经元经典电路模型和介观电路模型. 利用经典电路理论和介观电路的量子理论, 推导了在外部冲击激励下神经元细胞膜电压响应的表达式. 将枪乌贼神经元的电生理参数代入膜电压表达式并计算可知, 两种模型下的膜电压均先增大后减小, 最后达到零值的静息状态, 且其能量主要集中在0—30 Hz的脑电频率范围内. 进一步比较发现, 介观电路模型下膜电压的峰值及达到峰值所需的时间(达峰时间)均低于经典电路模型下的值, 并与枪乌贼轴突受到刺激后的实验结果更接近, 说明介观电路模型更能反应神经元受到刺激后的生理特征. 基于介观电路模型, 随着外部激励强度的增加, 膜电压的峰值增加且达峰时间变短. 膜电压峰值及达峰时间等参数更易受神经元膜电容的影响. 神经元的介观电路模型对于理解神经元受到刺激后的兴奋性, 推动受大脑功能启发的量子神经网络的发展等具有重要意义.
-
关键词:
- Hodgkin-Huxley神经元 /
- 电感 /
- 介观电路 /
- 量子理论
The size of neuron is on a mesoscopic scale. In this paper, considering the inductance characteristics of the neuron, the classical circuit model and mesoscopic circuit model of neuron including neuron membrane inductance, membrane capacitance, potassium ion memristor and chloride ion resistance are established. Based on the classical circuit theory and the quantum theory of mesoscopic circuit, the expression of neuron membrane voltage response under external impulse excitation is derived. Substituting the electrophysiological parameters of the squid neuron into the expression of membrane voltage, we find that the membrane voltages in both models first increase and then decrease, and finally reach their corresponding resting states of zero value, and their energy values are concentrated mainly in a range of 0–30 Hz in which the brainwave frequency is. Further comparisons show that the peak value of membrane voltage and the time required to reach the peak value (peak time) in the mesoscopic circuit model are lower than those in the classical circuit model, and are closer to the experimental results after the squid axon has been stimulated, indicating that the mesoscopic circuit model can better reflect the physiological characteristics of the stimulated neurons. Based on the mesoscopic circuit model, the peak value of membrane voltage increases and the peak time decreases with the increase of external excitation intensity. Parameters such as membrane voltage peak and peak time are more sensitive to the neuron membrane capacitance. The mesoscopic circuit model of the neuron is of great significance in understanding the excitability of the stimulated neuron and also in promoting the development of quantum neural networks inspired by brain function.-
Keywords:
- Hodgkin-Huxley neuron /
- inductance /
- mesoscopic circuit /
- quantum theory
[1] 徐泠风, 李传东, 陈玲 2016 65 240701
Google Scholar
Xu L F, Li C D, Chen L 2016 Acta Phys. Sin. 65 240701
Google Scholar
[2] 胡柏林, 马军, 李凡, 蒲忠胜 2013 62 058701
Google Scholar
Hu B L, Ma J, Li F, Pu Z S 2013 Acta Phys. Sin. 62 058701
Google Scholar
[3] 李佳佳, 吴莹, 独盟盟, 刘伟明 2015 64 030503
Google Scholar
Li J J, Wu Y, Du M M, Liu W M 2015 Acta Phys. Sin. 64 030503
Google Scholar
[4] 于文婷, 张娟, 唐军 2017 66 200201
Google Scholar
Yu W T, Zhang J, Tang J 2017 Acta Phys. Sin. 66 200201
Google Scholar
[5] Hodgkin A L, Huxley A F 1952 J. Physiol. 117 500
Google Scholar
[6] Diehl P U, Pedroni B U, Cassidy A, Merolla P, Neftci E, Zarrella G International Joint Conference on Neural Networks Vancouver, Canada, July 24–29, 2016 p4278
[7] Izhikevich E M 2003 IEEE Trans. Neural Networks 14 1569
Google Scholar
[8] 王宝燕, 徐伟, 邢真慈 2009 58 6590
Google Scholar
Wang B Y, Xu W, Xing Z C 2009 Acta Phys. Sin. 58 6590
Google Scholar
[9] Kalay Z 2011 Crit. Rev. Biochem. Mol. Biol. 46 310
Google Scholar
[10] Kampen N G V 2007 Stochastic Processes in Physics and Chemistry (3rd Ed.) (Amsterdam: Elsevier) pp422–428
[11] Chua L 2013 Nanotechnology 24 383001
Google Scholar
[12] Khodashenas M, Baghdadi G, Towhidkhah F 2019 J. Math. Neurosci. 9 4
Google Scholar
[13] Liu D, Zhao S, Luo X Y, Yuan Y 2019 Front. Neurosci. 13 1061
Google Scholar
[14] Zhang X J, Gu H G, Wu F Q 2019 Eur. Phys. J. -Spec. Top. 228 2053
Google Scholar
[15] Bao H, Zhang Y Z, Liu W B, Bao B C 2020 Nonlinear Dyn. 100 937
Google Scholar
[16] Baysal V, Saraç Z, Yilmaz E 2019 Nonlinear Dyn. 97 1275
Google Scholar
[17] Bossy M, Fontbona J, Olivero H 2018 J. Math. Biol. 78 1771
Google Scholar
[18] Wang R B, Wang Z Y, Zhu Z Y 2018 Nonlinear Dyn. 92 973
Google Scholar
[19] Wang Y H, Wang R B, Xu X Y 2017 Neural Plast. 2017 6207141
Google Scholar
[20] Zhu Z Y, Wang R B, Zhu F Y 2018 Front. Neurosci. 12 122
Google Scholar
[21] Pfeiffer P, Egusquiza I L, Di Ventra M, Sanz M, Solano E 2016 Sci. Rep. 6 29507
Google Scholar
[22] Salmilehto J, Deppe F, Di Ventra M, Sanz M, Solano E 2017 Sci. Rep. 7 42044
Google Scholar
[23] Sanz M, Lamata L, Solano E 2018 APL Photonics 3 080801
Google Scholar
[24] Gonzalez-Raya T, Cheng X H, Egusquiza I L, Chen X, Sanz M, Solano E 2019 Phys. Rev. Appl. 12 014037
Google Scholar
[25] Killoran N, Bromley T R, Arrazola J M, Schuld M, Quesada N, Lloyd S 2019 Phys. Rev. Res. 1 033063
Google Scholar
[26] Perdomo-Ortiz A, Benedetti M, Realpe-Gómez J, Biswas R 2018 Quantum Sci. Technol. 3 030502
Google Scholar
[27] Schuld M, Killoran N 2019 Phys. Rev. Lett. 122 040504
Google Scholar
[28] Cole K S, Baker R F 1941 J. Gen. Physiol. 24 771
Google Scholar
[29] Hodgkin A L 1951 Biol. Rev. 26 339
Google Scholar
[30] Kumai T 2017 Biophys. Physicobiol. 14 147
Google Scholar
[31] Wang R B, Zhang Z K, Jiao X F 2006 Appl. Phys. Lett. 89 123903
Google Scholar
[32] 周霆 2013 浙江大学学报(理学版) 40 285
Zhou T 2013 J. Zhejiang Univ. (Sci. Ed.) 40 285 (in Chinese)
[33] Caldeira A O, Leggett A J 1983 Ann. Phys. 149 374
Google Scholar
[34] Luo C H, Rudy Y 1991 Circ. Res. 68 1501
Google Scholar
-
图 1 神经元及其电路模型 (a) 神经元的结构; (b) 感性神经元的经典电路模型
Fig. 1. Neuron and its circuit model: (a) Structure of the neuron; (b) classical circuit model of the inductive neuron.
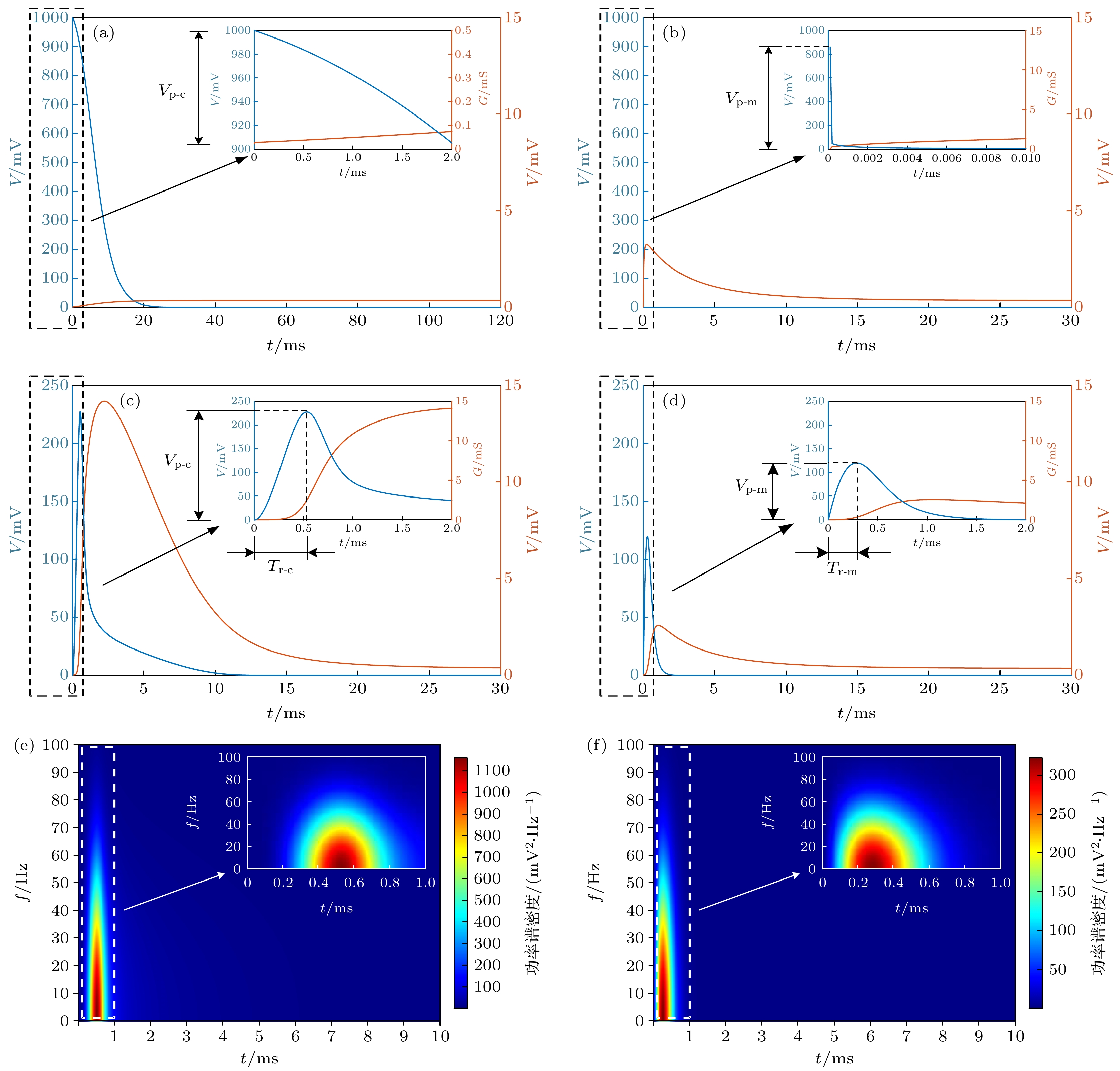
图 3 冲击输入下神经元的动力学响应 (a), (b) 分别为传统HH单离子通道神经元经典和介观电路模型下膜电压(蓝色)和K+电导(红色)随时间变化的曲线; (c), (d) 分别为感性神经元经典和介观电路模型下膜电压(蓝色)和K+电导(红色)随时间变化的曲线; (e), (f) 分别为感性神经元经典和介观电路模型下膜电压的时频功率密度谱图
Fig. 3. Dynamic response of a neuron under impulse input: (a), (b) The curves of membrane voltage (blue) and K+ conductivity (red) versus time obtained by solving classical and mesoscopic circuit models of the traditional HH single ion-channel neuron, respectively; (c), (d) the curves of membrane voltage (blue) and K+ conductivity (red) versus time obtained by solving the classical and mesoscopic circuit models of the inductive neuron, respectively; (e), (f) the time-frequency spectrogram of the membrane voltage obtained by solving the classical and mesoscopic circuit models of the inductive neuron, respectively.
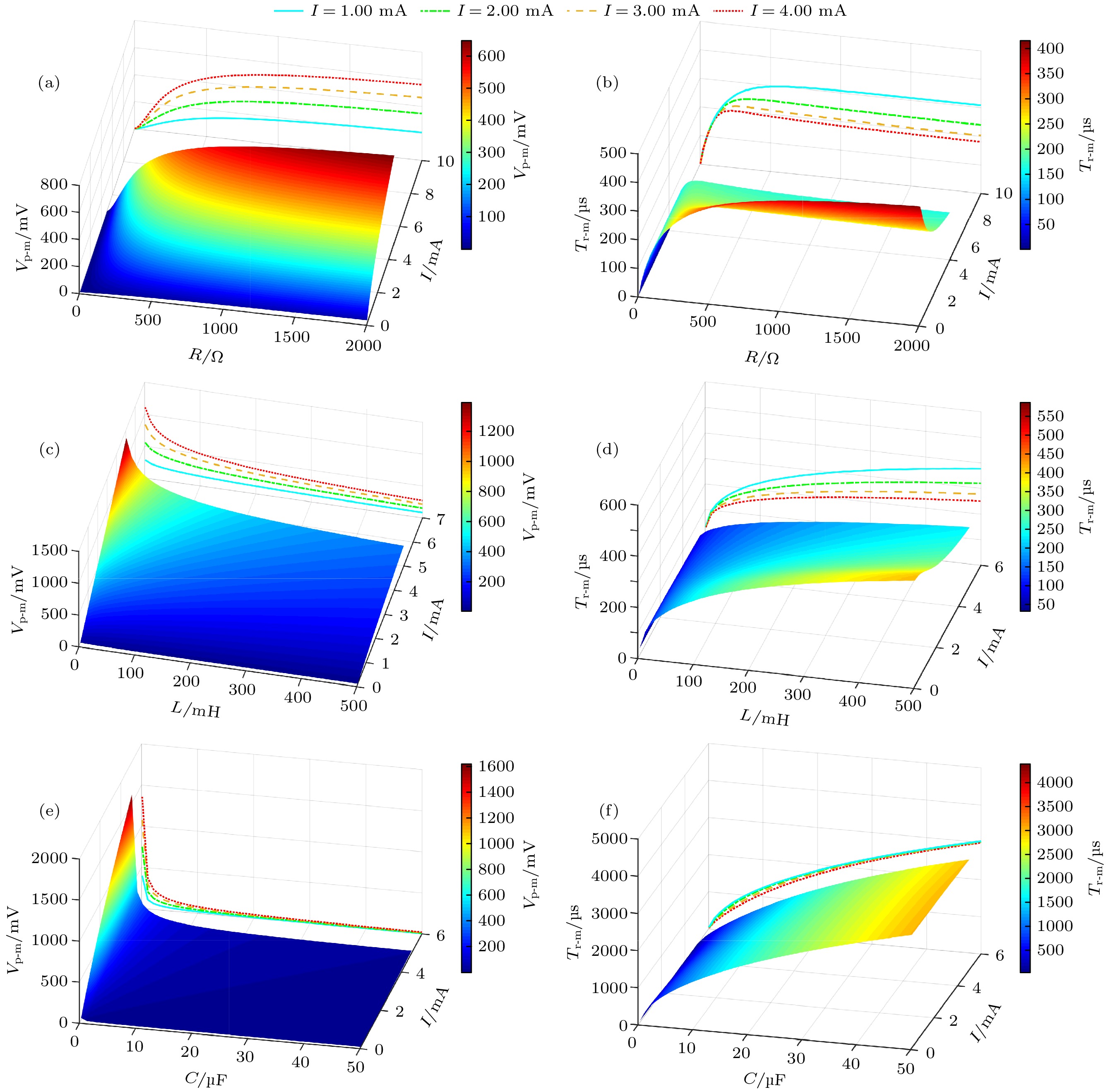
图 4 感性神经元介观电路模型中膜电压输出响应与外部激励和神经元内部参数的关系 (a), (c), (e) 分别为Vp-m随I, R, L和C的变化曲线; (b), (d), (f)分别为Tr-m随I, R, L和C的变化曲线
Fig. 4. The relationship between the output response of the membrane voltage in the mesoscopic circuit model of inductive neuron and the external excitation and the internal parameters of the neuron: (a), (c), (e) The dependence curves of Vp-m on I, R, L and C, respectively; (b), (d), (f) the dependence curves of Tr-m on I, R, L and C, respectively.
表 1 感性神经元的Vp-m和Tr-m对神经元内部参数的灵敏度
Table 1. Sensitivity of Vp-m and Tr-m of the inductive neuron to the internal parameters.
电流幅值I/mA 1 2 3 4 max(dVp-m/dR) /(mV·mΩ–1) 3.90 × 10–4 7.75 × 10–4 11.74 × 10–4 15.44 × 10–4 max(dVp-m/dL) (mV·mH–1) –1.19 × 10–2 –2.15 × 10–2 –2.97 × 10–2 –3.67 × 10–2 max(dVp-m/dC) (mV·mF–1) –2.60 × 10–2 –5.20 × 10–2 –7.90 × 10–2 –10.46 × 10–2 max(dTr-m/dR) (μs·mΩ–1) 2.53 × 10–3 2.50 × 10–3 2.47 × 10–3 2.41 × 10–3 max(dTr-m/dL) (μs·mH–1) 6.47 6.17 5.87 5.38 max(dTr-m/dC) (μs·mF–1) 2.53 × 105 2.18 × 105 1.91 × 105 1.73 × 105 
下载: 导出CSV
-
[1] 徐泠风, 李传东, 陈玲 2016 65 240701
Google Scholar
Xu L F, Li C D, Chen L 2016 Acta Phys. Sin. 65 240701
Google Scholar
[2] 胡柏林, 马军, 李凡, 蒲忠胜 2013 62 058701
Google Scholar
Hu B L, Ma J, Li F, Pu Z S 2013 Acta Phys. Sin. 62 058701
Google Scholar
[3] 李佳佳, 吴莹, 独盟盟, 刘伟明 2015 64 030503
Google Scholar
Li J J, Wu Y, Du M M, Liu W M 2015 Acta Phys. Sin. 64 030503
Google Scholar
[4] 于文婷, 张娟, 唐军 2017 66 200201
Google Scholar
Yu W T, Zhang J, Tang J 2017 Acta Phys. Sin. 66 200201
Google Scholar
[5] Hodgkin A L, Huxley A F 1952 J. Physiol. 117 500
Google Scholar
[6] Diehl P U, Pedroni B U, Cassidy A, Merolla P, Neftci E, Zarrella G International Joint Conference on Neural Networks Vancouver, Canada, July 24–29, 2016 p4278
[7] Izhikevich E M 2003 IEEE Trans. Neural Networks 14 1569
Google Scholar
[8] 王宝燕, 徐伟, 邢真慈 2009 58 6590
Google Scholar
Wang B Y, Xu W, Xing Z C 2009 Acta Phys. Sin. 58 6590
Google Scholar
[9] Kalay Z 2011 Crit. Rev. Biochem. Mol. Biol. 46 310
Google Scholar
[10] Kampen N G V 2007 Stochastic Processes in Physics and Chemistry (3rd Ed.) (Amsterdam: Elsevier) pp422–428
[11] Chua L 2013 Nanotechnology 24 383001
Google Scholar
[12] Khodashenas M, Baghdadi G, Towhidkhah F 2019 J. Math. Neurosci. 9 4
Google Scholar
[13] Liu D, Zhao S, Luo X Y, Yuan Y 2019 Front. Neurosci. 13 1061
Google Scholar
[14] Zhang X J, Gu H G, Wu F Q 2019 Eur. Phys. J. -Spec. Top. 228 2053
Google Scholar
[15] Bao H, Zhang Y Z, Liu W B, Bao B C 2020 Nonlinear Dyn. 100 937
Google Scholar
[16] Baysal V, Saraç Z, Yilmaz E 2019 Nonlinear Dyn. 97 1275
Google Scholar
[17] Bossy M, Fontbona J, Olivero H 2018 J. Math. Biol. 78 1771
Google Scholar
[18] Wang R B, Wang Z Y, Zhu Z Y 2018 Nonlinear Dyn. 92 973
Google Scholar
[19] Wang Y H, Wang R B, Xu X Y 2017 Neural Plast. 2017 6207141
Google Scholar
[20] Zhu Z Y, Wang R B, Zhu F Y 2018 Front. Neurosci. 12 122
Google Scholar
[21] Pfeiffer P, Egusquiza I L, Di Ventra M, Sanz M, Solano E 2016 Sci. Rep. 6 29507
Google Scholar
[22] Salmilehto J, Deppe F, Di Ventra M, Sanz M, Solano E 2017 Sci. Rep. 7 42044
Google Scholar
[23] Sanz M, Lamata L, Solano E 2018 APL Photonics 3 080801
Google Scholar
[24] Gonzalez-Raya T, Cheng X H, Egusquiza I L, Chen X, Sanz M, Solano E 2019 Phys. Rev. Appl. 12 014037
Google Scholar
[25] Killoran N, Bromley T R, Arrazola J M, Schuld M, Quesada N, Lloyd S 2019 Phys. Rev. Res. 1 033063
Google Scholar
[26] Perdomo-Ortiz A, Benedetti M, Realpe-Gómez J, Biswas R 2018 Quantum Sci. Technol. 3 030502
Google Scholar
[27] Schuld M, Killoran N 2019 Phys. Rev. Lett. 122 040504
Google Scholar
[28] Cole K S, Baker R F 1941 J. Gen. Physiol. 24 771
Google Scholar
[29] Hodgkin A L 1951 Biol. Rev. 26 339
Google Scholar
[30] Kumai T 2017 Biophys. Physicobiol. 14 147
Google Scholar
[31] Wang R B, Zhang Z K, Jiao X F 2006 Appl. Phys. Lett. 89 123903
Google Scholar
[32] 周霆 2013 浙江大学学报(理学版) 40 285
Zhou T 2013 J. Zhejiang Univ. (Sci. Ed.) 40 285 (in Chinese)
[33] Caldeira A O, Leggett A J 1983 Ann. Phys. 149 374
Google Scholar
[34] Luo C H, Rudy Y 1991 Circ. Res. 68 1501
Google Scholar
下载:
计量
- 文章访问数: 5048
- PDF下载量: 102
- 被引次数: 0
