-
The diffusion dynamics of a particle in the biased disorder medium is investigated in this paper. Based on the mean first passage time (MFPT) theory, the analytical approximate expression of effective diffusion coefficient of a particle in the biased disorder potential is obtained. The results show that the effective diffusion of a particle in the biased disorder potential is significantly enhanced. We explain the enhancement mechanism by using the wave packet broadening of probability density distribution function. In addition, we propose the concepts of effective kinetic temperature and effective friction, and further find that the effective diffusion behavior of a particle strongly depends on the biased force.
-
Keywords:
- disorder /
- random correlation potential /
- diffusion enhancement
[1] Su Y, Ma X G, Lai P, Tong P 2017 Soft Matter 13 4773
Google Scholar
[2] Lindenberg K, Sancho J M, Khoury M, Lacasta A M 2012 Fluctuation Noise Lett. 11 1240004
Google Scholar
[3] Zwanzig R 1988 Proc. Natl. Acad. Sci. U.S.A. 85 2029
Google Scholar
[4] Lifson S, Jackson J L 1962 J. Chem. Phys. 36 2410
Google Scholar
[5] Longobardi L, Massarotti D, Rotoli G, Stornaiuolo D, Papari G, Kawakami A, Pepe G P, Barone A, Tafuri F 2011 Phys. Rev. B 84 184504
Google Scholar
[6] Fulde P, Pietronero L, Schneider W R, Strässler S 1975 Phys. Rev. Lett. 35 1776
Google Scholar
[7] Kurrer C, Schulten K 1995 Phys. Rev. E 51 6213
Google Scholar
[8] Reimann P 2002 Phys. Rep. 361 57
Google Scholar
[9] Lee S H, Grier D G 2006 Phys. Rev. Lett. 96 190601
Google Scholar
[10] Blickle V, Speck T, Seifert U, Bechinger C 2007 Phys. Rev. E 75 060101
Google Scholar
[11] Schiavoni M, Sanchez-Palencia L, Renzoni F, Grynberg G 2003 Phys. Rev. Lett. 90 094101
Google Scholar
[12] Lü K, Bao J D 2007 Phys. Rev. E 76 061119
Google Scholar
[13] Shi X Y, Bao J D 2019 Physica A 514 203
Google Scholar
[14] Gleeson J P, Sancho J M, Lacasta A M, Lindenberg K 2006 Phys. Rev. E 73 041102
Google Scholar
[15] Khoury M, Lacasta A M, Sancho J M, Lindenber K 2011 Phys. Rev. Lett. 106 090602
Google Scholar
[16] Slutsky M, Kardar M, Mirny L A 2004 Phys. Rev. E 69 061903
Google Scholar
[17] Bouchaud J P, Georges A 1990 Phys. Rep. 195 127
Google Scholar
[18] Hänggi P, Talkner P, Borkovec M 1990 Rev. Mod. Phys. 62 251
Google Scholar
[19] Hanes R D L, Dalle-Ferrier C, Schmiedeberg M, Jenkins M C, Egelhaaf S U 2012 Soft Matter 8 2714
Google Scholar
[20] Harris S J, Timmons A, Baker D R, Monroe C 2010 Chem. Phys. Lett. 485 265
Google Scholar
[21] Sieminskas L, Ferguson M, Zerda T W, Couch E 1997 J. Sol-Gel Sci. Technol. 8 1105
Google Scholar
[22] Kafri K, Lubensky D K, Nelson D R 2004 Biophys. J. 86 3373
Google Scholar
[23] Smith P, Morrison I E G, Wilson K M, Fernandez N, Cherry R J 1999 Biophys. J. 76 3331
Google Scholar
[24] Hyeon C, Thirumalai D 2003 Proc. Natl. Acad. Sci. U.S.A. 100 10249
Google Scholar
[25] Reimann P, Van den Broeck C, Linke H, Hänggi P, Rub J M, Perez-Madrid A 2001 Phys. Rev. Lett. 87 010602
Google Scholar
[26] Reimann P, Van den Broeck C, Linke H, Hänggi P, Rub J M, Perez-Madrid A 2002 Phys. Rev. E 65 031104
Google Scholar
[27] Evstigneev M, Zvyagolskaya O, Bleil S, Eichhorn R, Bechinger C, Reimann P 2008 Phys. Rev. E 77 041107
Google Scholar
[28] Lindner B 2010 New J. Phys. 12 063026
Google Scholar
[29] Simon M S, Sancho J M, Lacasta A M 2012 Fluctuation Noise Lett. 11 1250026
Google Scholar
[30] Simon M S, Sancho J M, Lindenberg K 2013 Phys. Rev. E 88 062105
Google Scholar
[31] 包景东 2009 经典和量子耗散系统的随机模拟方法 (北京: 科学出版社) 第111页
Bao J D 2009 Random Simulation Method of Classical and Quantum Dissipation System (Beijing: Science Press) p111 (in Chinese)
[32] Hu M, Bao J D 2018 Phys. Rev. E 97 062143
Google Scholar
[33] Bao J D, Liu J 2013 Phys. Rev. E 88 022153
Google Scholar
[34] Reimann P, Eichhorn R 2008 Phys. Rev. Lett. 101 180601
Google Scholar
[35] Nixon G I, Slater G W 1996 Phys. Rev. E 53 4969
Google Scholar
[36] Yeh D C, Huntington H B 1984 Phys. Rev. Lett. 53 1469
Google Scholar
[37] Coh S, Gannett W, Zettl A, Cohen M L, Louie S G 2013 Phys. Rev. Lett. 110 185901
Google Scholar
[38] Berkovich R, Garcia-Manes S, Urbakh M, Klafter J, Fernandez J M 2010 Biophys. J. 98 2692
Google Scholar
[39] Smith S B, Cui Y J, Bustamante C 1996 Science 271 795
Google Scholar
[40] Liphardt J, Onoa B, Smith S B, Tinoco Jr. I, Bustamante C 2001 Science 292 733
Google Scholar
-
图 1 偏压OU-RCP及OU的空间导数RCP示意图. 参数选取为
$ \tilde{\lambda} = 0.5 $ ,$ \tilde{D} = 0.1 $ ,$ \tilde{F} = 0.8 $ Fig. 1. The schematic diagram of the biased OU-RCP and the derivative of OU-RCP. The parameters used are
$ \tilde{\lambda} = 0.5 $ ,$ \tilde{D} = 0.1 $ ,$ \tilde{F} = 0.8 $ .
图 2 偏压随机势中粒子的有效扩散系数
$ D_{\rm eff} $ 随$ \tilde{F} $ 的变化. 这里比较了OU-RCP和OU的导数RCP中的结果. 内图: 继续增大$ \tilde{F} $ , OU的导数RCP对应的绿色方块曲线的变化趋势. 参数选取为$ \tilde{\lambda} = 0.5 $ ,$ \tilde{D} = 0.1 $ Fig. 2. Dependence of the effective diffusion coefficient
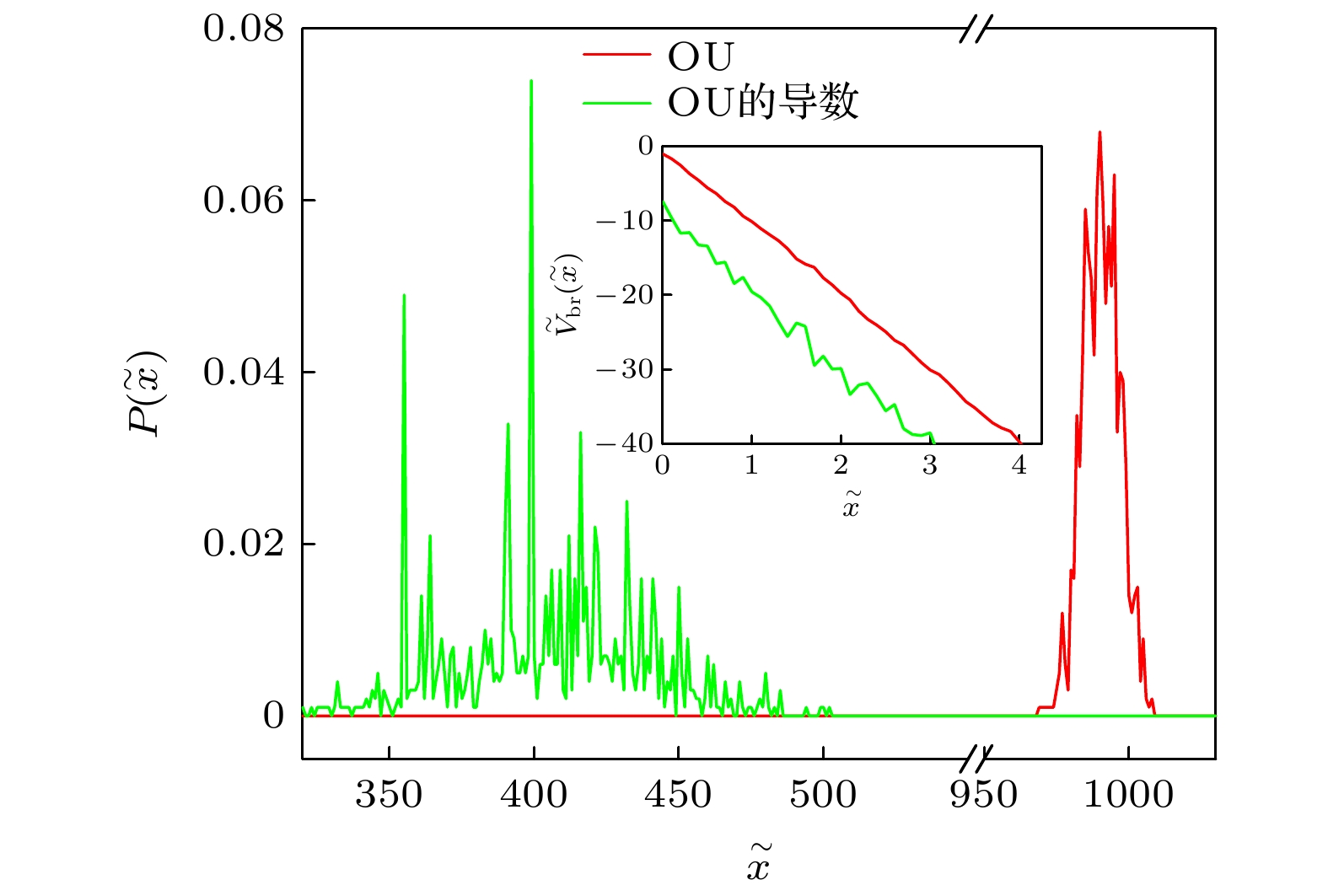
$ D_{\rm eff} $ on the biased force$ \tilde{F} $ in$ \tilde{V}_{\rm br} $ . Here, the results of OU-RCP and OU’s derivative RCP are compared. Illustration: The trend of the green square curve when continuing to increase$ \tilde{F} $ . The parameters used are$ \tilde{\lambda} = 0.5 $ ,$ \tilde{D} = 0.1 $ .
图 3 分别叠加OU-RCP, OU的导数RCP的偏压随机势中粒子的概率密度分布函数. 内图: 叠加OU-RCP, OU的导数RCP的偏压随机势
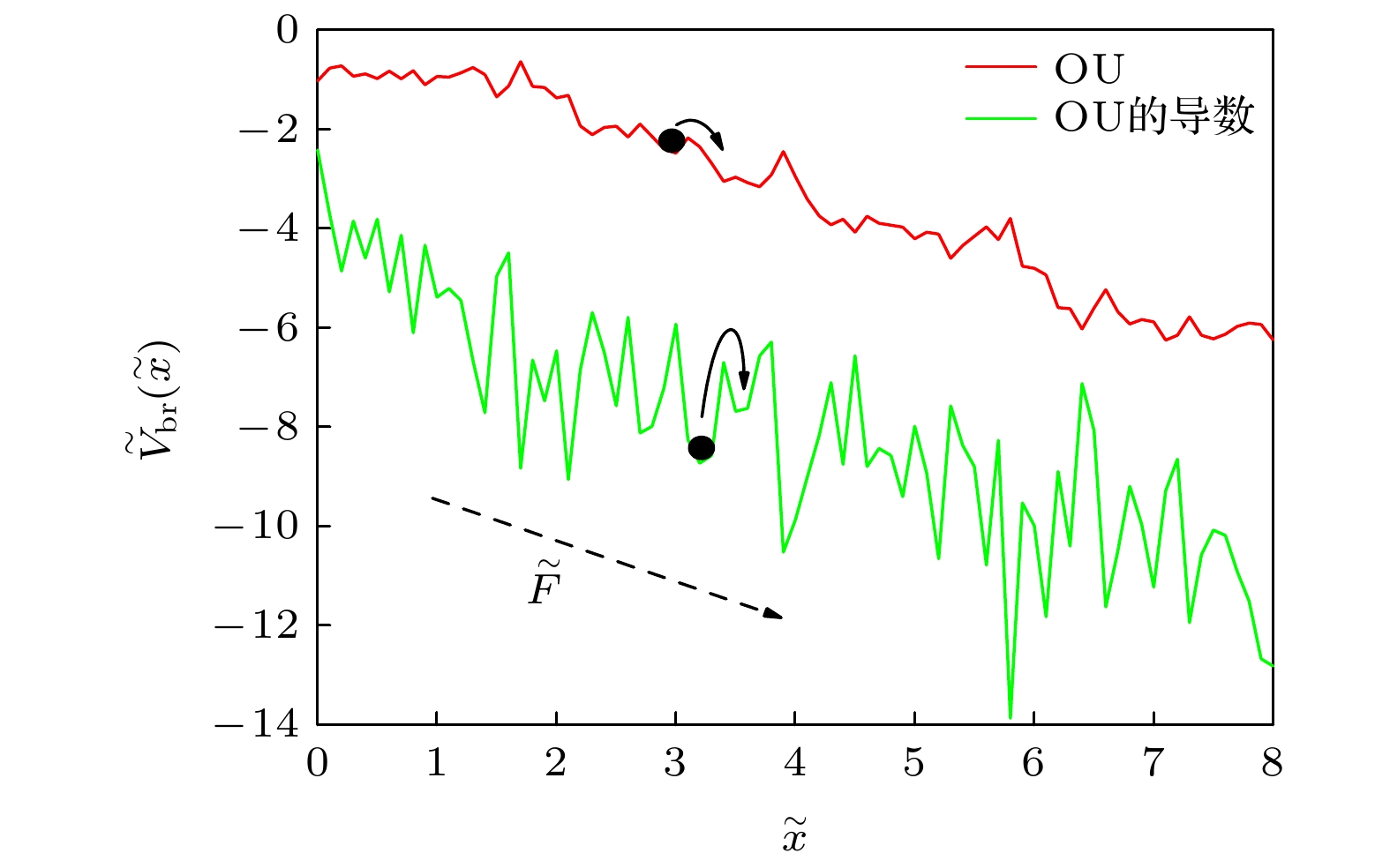
$ V_{\rm br} $ 的示意图. 参数选取为$ \tilde{\lambda} = 0.5 $ ,$ \tilde{D} = 0.1 $ ,$ \tilde{F} = 10.0 $ Fig. 3. The PDF of a particle in
$ V_{\rm br} $ , the OU-RCP and OU’s derivative RCP are considered. Illustration: the schematic diagram of$ V_{\rm br} $ . The parameters used are$\tilde{\lambda} = $ $ 0.5$ ,$ \tilde{D} = 0.1 $ ,$ \tilde{F} = 10.0 $ 
图 4 3种势
$ \tilde{V}_{\rm br} $ ,$ \tilde{V}_{\rm bpr} $ 和$ \tilde{V}_{\rm bp} $ 中粒子的有效扩散系数$ D_{\rm eff} $ 作为偏压力$ \tilde{F} $ 的函数. 比较了解析和模拟结果. 参数选取为$ \tilde{\lambda} = 0.5 $ ,$ \tilde{D} = 0.1 $ Fig. 4. The effective diffusion coefficient
$ D_{\rm eff} $ of a particle as a function of the biased force$ \tilde{F} $ in$ \tilde{V}_{\rm br} $ ,$ \tilde{V}_{\rm bpr} $ and$ \tilde{V}_{\rm bp} $ . The analytical result and simulation result are compared. The parameters used are$ \tilde{\lambda} = 0.5 $ ,$ \tilde{D} = 0.1 $ .
图 5
$ \tilde{F} = 1.0 $ 时,$ \tilde{V}_{\rm bp} $ ,$ \tilde{V}_{\rm br} $ 及$ \tilde{V}_{\rm bpr} $ 中粒子的概率密度分布函数($(\rm a)—(\rm c)$ ); (d)$ \tilde{F} = 1.7 $ (图4的红线加三角形曲线的最大值对应的偏压力)时,$ \tilde{V}_{\rm bpr} $ 中粒子的概率密度分布函数. 内图:$ \tilde{F} = 1.0 $ 时的$ \tilde{V}_{\rm br} $ ,$ \tilde{V}_{\rm bpr} $ 示意图. 参数选取为$ \tilde{\lambda} = 0.5 $ ,$ \tilde{D} = 0.1 $ Fig. 5. The PDF corresponding to
$ \tilde{V}_{\rm bp} $ ,$ \tilde{V}_{\rm br} $ and$ \tilde{V}_{\rm bpr} $ for$ \tilde{F} = 1.0 $ ((a)–(c)); (d) the PDF of particle in$ \tilde{V}_{\rm bpr} $ for$ \tilde{F} = 1.7 $ (the optimal biased force for$ \tilde{V}_{\rm bpr} $ in Fig. 4). Illustration: the schematic diagram of$ \tilde{V}_{\rm br} $ ,$ \tilde{V}_{\rm bpr} $ for$ \tilde{F} = 1.0 $ . The parameters used are$ \tilde{\lambda} = 0.5 $ ,$ \tilde{D} = 0.1 $ .表 1 3种势结构下粒子的有效动力学温度
$k_{\rm B}T^*$ 及有效阻尼$\gamma^*$ 随偏压力的变化Table 1. The effective kinetic temperature
$k_{\rm B}T^*$ and effective friction$\gamma^*$ of a particle under the three potential structures change with the biased force.$\tilde F=0$ 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 偏压周期势 $k_{\rm B}T^*$
$\gamma^*$0.20
95.120.21
4.110.45
0.470.42
1.060.32
1.480.28
1.30.25
1.20.24
1.170.23
1.09偏压周期随机势 $k_{\rm B}T^*$
$\gamma^*$0.20
360.320.21
200.620.22
8.560.36
0.221.09
0.060.62
0.070.32
0.840.31
0.600.23
1.31偏压随机势 $k_{\rm B}T^*$
$\gamma^*$0.20
77.430.22
10.280.28
0.830.62
0.131.09
0.080.34
0.090.25
1.210.26
0.670.27
1.30
下载: 导出CSV
-
[1] Su Y, Ma X G, Lai P, Tong P 2017 Soft Matter 13 4773
Google Scholar
[2] Lindenberg K, Sancho J M, Khoury M, Lacasta A M 2012 Fluctuation Noise Lett. 11 1240004
Google Scholar
[3] Zwanzig R 1988 Proc. Natl. Acad. Sci. U.S.A. 85 2029
Google Scholar
[4] Lifson S, Jackson J L 1962 J. Chem. Phys. 36 2410
Google Scholar
[5] Longobardi L, Massarotti D, Rotoli G, Stornaiuolo D, Papari G, Kawakami A, Pepe G P, Barone A, Tafuri F 2011 Phys. Rev. B 84 184504
Google Scholar
[6] Fulde P, Pietronero L, Schneider W R, Strässler S 1975 Phys. Rev. Lett. 35 1776
Google Scholar
[7] Kurrer C, Schulten K 1995 Phys. Rev. E 51 6213
Google Scholar
[8] Reimann P 2002 Phys. Rep. 361 57
Google Scholar
[9] Lee S H, Grier D G 2006 Phys. Rev. Lett. 96 190601
Google Scholar
[10] Blickle V, Speck T, Seifert U, Bechinger C 2007 Phys. Rev. E 75 060101
Google Scholar
[11] Schiavoni M, Sanchez-Palencia L, Renzoni F, Grynberg G 2003 Phys. Rev. Lett. 90 094101
Google Scholar
[12] Lü K, Bao J D 2007 Phys. Rev. E 76 061119
Google Scholar
[13] Shi X Y, Bao J D 2019 Physica A 514 203
Google Scholar
[14] Gleeson J P, Sancho J M, Lacasta A M, Lindenberg K 2006 Phys. Rev. E 73 041102
Google Scholar
[15] Khoury M, Lacasta A M, Sancho J M, Lindenber K 2011 Phys. Rev. Lett. 106 090602
Google Scholar
[16] Slutsky M, Kardar M, Mirny L A 2004 Phys. Rev. E 69 061903
Google Scholar
[17] Bouchaud J P, Georges A 1990 Phys. Rep. 195 127
Google Scholar
[18] Hänggi P, Talkner P, Borkovec M 1990 Rev. Mod. Phys. 62 251
Google Scholar
[19] Hanes R D L, Dalle-Ferrier C, Schmiedeberg M, Jenkins M C, Egelhaaf S U 2012 Soft Matter 8 2714
Google Scholar
[20] Harris S J, Timmons A, Baker D R, Monroe C 2010 Chem. Phys. Lett. 485 265
Google Scholar
[21] Sieminskas L, Ferguson M, Zerda T W, Couch E 1997 J. Sol-Gel Sci. Technol. 8 1105
Google Scholar
[22] Kafri K, Lubensky D K, Nelson D R 2004 Biophys. J. 86 3373
Google Scholar
[23] Smith P, Morrison I E G, Wilson K M, Fernandez N, Cherry R J 1999 Biophys. J. 76 3331
Google Scholar
[24] Hyeon C, Thirumalai D 2003 Proc. Natl. Acad. Sci. U.S.A. 100 10249
Google Scholar
[25] Reimann P, Van den Broeck C, Linke H, Hänggi P, Rub J M, Perez-Madrid A 2001 Phys. Rev. Lett. 87 010602
Google Scholar
[26] Reimann P, Van den Broeck C, Linke H, Hänggi P, Rub J M, Perez-Madrid A 2002 Phys. Rev. E 65 031104
Google Scholar
[27] Evstigneev M, Zvyagolskaya O, Bleil S, Eichhorn R, Bechinger C, Reimann P 2008 Phys. Rev. E 77 041107
Google Scholar
[28] Lindner B 2010 New J. Phys. 12 063026
Google Scholar
[29] Simon M S, Sancho J M, Lacasta A M 2012 Fluctuation Noise Lett. 11 1250026
Google Scholar
[30] Simon M S, Sancho J M, Lindenberg K 2013 Phys. Rev. E 88 062105
Google Scholar
[31] 包景东 2009 经典和量子耗散系统的随机模拟方法 (北京: 科学出版社) 第111页
Bao J D 2009 Random Simulation Method of Classical and Quantum Dissipation System (Beijing: Science Press) p111 (in Chinese)
[32] Hu M, Bao J D 2018 Phys. Rev. E 97 062143
Google Scholar
[33] Bao J D, Liu J 2013 Phys. Rev. E 88 022153
Google Scholar
[34] Reimann P, Eichhorn R 2008 Phys. Rev. Lett. 101 180601
Google Scholar
[35] Nixon G I, Slater G W 1996 Phys. Rev. E 53 4969
Google Scholar
[36] Yeh D C, Huntington H B 1984 Phys. Rev. Lett. 53 1469
Google Scholar
[37] Coh S, Gannett W, Zettl A, Cohen M L, Louie S G 2013 Phys. Rev. Lett. 110 185901
Google Scholar
[38] Berkovich R, Garcia-Manes S, Urbakh M, Klafter J, Fernandez J M 2010 Biophys. J. 98 2692
Google Scholar
[39] Smith S B, Cui Y J, Bustamante C 1996 Science 271 795
Google Scholar
[40] Liphardt J, Onoa B, Smith S B, Tinoco Jr. I, Bustamante C 2001 Science 292 733
Google Scholar
下载:
计量
- 文章访问数: 4680
- PDF下载量: 42
- 被引次数: 0
