-
标度拓展经典负半阶分抗逼近电路, 可实现具有任意分数阶微积算子运算功能的分抗逼近电路, 但牺牲了运算恒定性. 从电路网络的角度分析具有恒定运算性能的负半阶Carlson分形格分抗逼近电路. 根据标度分形格分抗逼近电路的等效无源双口网络, 探讨该双口网络右侧端口的运算有效性, 设计具有高运算恒定性的任意阶标度分形格分抗逼近电路. 结合负实零极点对基元系统的零极点分布及其局域化特性, 阐述具有任意实数阶微积算子运算功能的标度分形格分抗逼近电路运算振荡现象的物理本质, 并从理论上分析有效抑制频域运算振荡现象的方法. 结合对称阻容T型节电路优化理论及方法, 对任意阶对称格型级联双口网络的频域逼近性能进行优化, 获得具有高逼近效益的任意阶标度分形格分抗逼近电路. 具有低振荡幅度的任意阶对称格型级联双口网络为高运算恒定性的分抗逼近电路设计及应用提供了一种新方法及思路.Fractional calculus is widely used in the analysis and description of various nonlinear and non-integer dimensional physical phenomena and processes in nature, and it gradually becomes a research hotspot. The order value of fractional-order system is more flexible, and fractional-order system is more accurate for analysis of non-integer dimensional physical phenomena and processes. In recent years, various negative half-order fractance approximation circuits and rational approximation algorithms for negative half-order fractional operators have been proposed and aroused people's research interest. The scaling extension of classic negative half-order fractance approximation circuits can facilitate the design of fractance approximation circuits with arbitrary-order fractional operators, but the operational constancy is sacrificed. The typical arbitrary-order fractance approximation circuits have operational oscillating phenomena in frequency domain, both the order-frequency characteristic curves and the phase-frequency characteristic curves have obvious oscillating waveforms. The operational oscillating phenomena will inevitably affect the fractional operator operational performance of the fractance approximation circuits, and result in errors in physical application. In this paper, the negative half-order Carlson fractal-lattice fractance approximation circuit with constant operational performance is analyzed from perspective of circuit network, the symmetry for equivalent two-port network of Carlson fractal-lattice fractance approximate circuit is analyzed. The equivalent two-port network of scaling fractal-lattice fractance approximation circuit is explored, Operational validity for the right port of scaling lattice cascaded two-port network is studied. A symmetrical lattice cascaded passive two-port network after scaling extension is designed through cascade of the ports on both sides of two-port network, and an arbitrary-order scaling fractal-lattice fractance approximation circuit with high-operation constancy is designed. By studying the zero-pole distribution and localization characteristics of the negative real zero-pole pair elemental unit, the physical nature of operational oscillating phenomenon for scaling fractal-lattice fractance approximation circuit with the operational performance of arbitrary-order fractional operator is explained theoretically, the methods and ideas to effectively suppress frequency-domain operational oscillating phenomenon are theoretically analyzed. The physical nature of operational oscillating amplitude reduction is explained by contrastively analyzing the pole-zero distributions of scaling fractal-lattice fractance approximation circuit and symmetrical lattice cascaded two-port network. According to the optimization principle of arbitrary-order fractance approximation circuits, the symmetrical resistor-capacitor T-section circuit optimization methods are used to optimize the frequency-domain approximation performance of any real-order symmetrical lattice cascaded two-port network, and it contributes to obtain any real-order scaling fractal-lattice fractance approximation circuit with high benefit of approximation. Arbitrary-order symmetrical lattice cascaded two-port network provides methods and ideas for the design of fractance approximation circuits with high-operation constancy.
-
Keywords:
- fractional calculus /
- scaling extension /
- fractional order element /
- operational constancy
[1] Karamali G, Dehghan M, Abbaszadeh M 2019 Eng. Comput.-Germany. 35 87
Google Scholar
[2] Oldham K B 1991 J. Appl. Electrochem. 21 1068
Google Scholar
[3] Su Y, Wang Y 2019 J. Funct. Space 2019 1
[4] Hamrouni W, Abdennadher A 2016 Discrete Cont. Dyn-B 21 2509
Google Scholar
[5] Wu G C, Baleanu D, Deng Z G, Zeng S D 2015 Physica A 438 335
Google Scholar
[6] Hamed E M, Said L A, Madian A H, Radwan A G 2020 Circ. Syst. Signal Pr. 39 2
Google Scholar
[7] Ali Yüce, Tan N 2020 J. Eng. 2020 157
Google Scholar
[8] Subhadhra K S, Sharma R K, Gupta S S 2020 Analog Integr. Circuits Signal Process. 103 31
Google Scholar
[9] Hamed E M, Said L A, Madian A H, Radwan A G 2020 Circuits, Systems, and Signal Processing 39 2
[10] Yu B, Pu Y F, He Q Y 2020 J. Circuits Syst. Comput. 29 2050083
Google Scholar
[11] Atan O 2018 Analog Integr. Circuits Signal Process. 96 485
Google Scholar
[12] Mahmoud G M, Abed-Elhameed T M, Ahmed M E 2016 Nonlinear Dyn. 83 1885
Google Scholar
[13] Yang S, Yu J, Hu C, Jiang H 2018 Neural Networks 104 104
Google Scholar
[14] 袁晓 2015 分抗逼近电路之数学原理 (北京: 科学出版社) 第3—15
Yuan X 2015 Mathematical Principles of Fractance Approximation Circuits (Beijing: Science Press) pp3–15 (in Chinese)
[15] Dutta R, Suhash C, Shenoi B A 1966 J. Franklin Inst. 282 318
Google Scholar
[16] Oldham K B 1973 Anal. Chem. 45 39
[17] 袁子, 袁晓 2017 电子学报 45 2511
Google Scholar
Yuan Z, Yuan X 2017 Acta Electron. Sin. 45 2511
Google Scholar
[18] Hill R M, Dissado L A, Nigmatullin R R 1991 J. Phys. Condens. Matter 3 9773
Google Scholar
[19] Liu S H 1985 Phys. Rev. Lett. 55 529
Google Scholar
[20] He Q Y, Pu Y F, Yu B, Yuan X 2019 Circuits Syst. Signal Process. 38 4933
Google Scholar
[21] 何秋燕, 袁晓 2016 65 160202
Google Scholar
He Q Y, Yuan X 2016 Acta Phys. Sin. 65 160202
Google Scholar
[22] He Q Y, Yu B, Yuan X 2017 Chin. Phys. B 26 040202
Google Scholar
[23] He Q Y, Pu Y F, Yu B 2020 Acta Autom. Sin. 7 1425
Google Scholar
[24] 袁晓, 冯国英 2015 中国电子学会电路与系统分会第二十六届学术年会论文集 中国长沙, 2015年10月23日−26日 第295页
Yuan X, Feng G Y 2015 Proceedings of the 26 th Academic Annual Conference of Circuits and Systems Branch, Chinese Institute of Electronics Chang Sha, China, October 23−26, 2015 p295
[25] 余波, 何秋燕, 袁晓 2018 67 070202
Google Scholar
Yu B, He Q Y, Yuan X 2018 Acta Phys. Sin. 67 070202
Google Scholar
[26] 余波, 何秋燕, 袁晓, 杨丽贤 2018 四川大学学报(自然科学版) 55 301
Google Scholar
Yu B, He Q Y, Yuan X, Yang L X 2018 J. Sichuan Univ.(Nat. Sci. Ed.) 55 301
Google Scholar
[27] Herzel F, Osmany S A, Scheytt J C 2010 IEEE Trans. Circuits Syst. Regul. Rap. 57 1914
Google Scholar
-
图 1 有限k节Carlson格型分抗逼近电路 (a) 归一化原型电路; (b) 等效双口网络
Fig. 1. Finite k-stage Carlson Lattice fractance approximation circuit: (a) Normalized prototype circuit; (b) equivalent two-port network
图 2 Carlson分形格分抗逼近电路的运算特征曲线 (a) 阶频特征曲线; (b) 相频特征曲线
Fig. 2. Operational characteristic curves of Carlson fractal-lattice fractance approximation circuit: (a) Order-frequency characteristic curves; (b) phase-frequency characteristic curves.
图 3 k节标度分形格分抗逼近电路 (a) 归一化原型电路; (b) 等效双口网络
Fig. 3. k-stage scaling fractal-lattice fractance approximation circuit: (a) Normalized prototype circuit; (b) equivalent two-port network
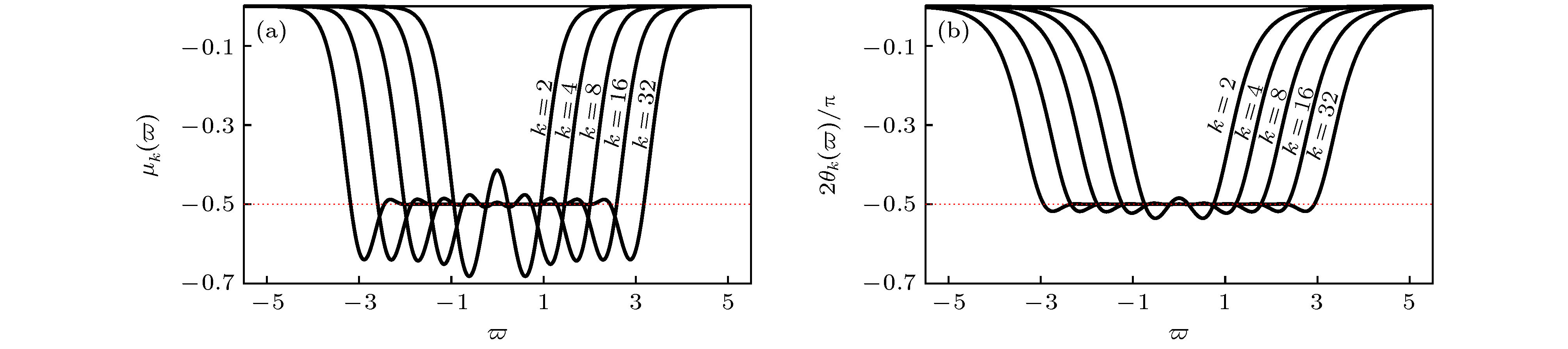
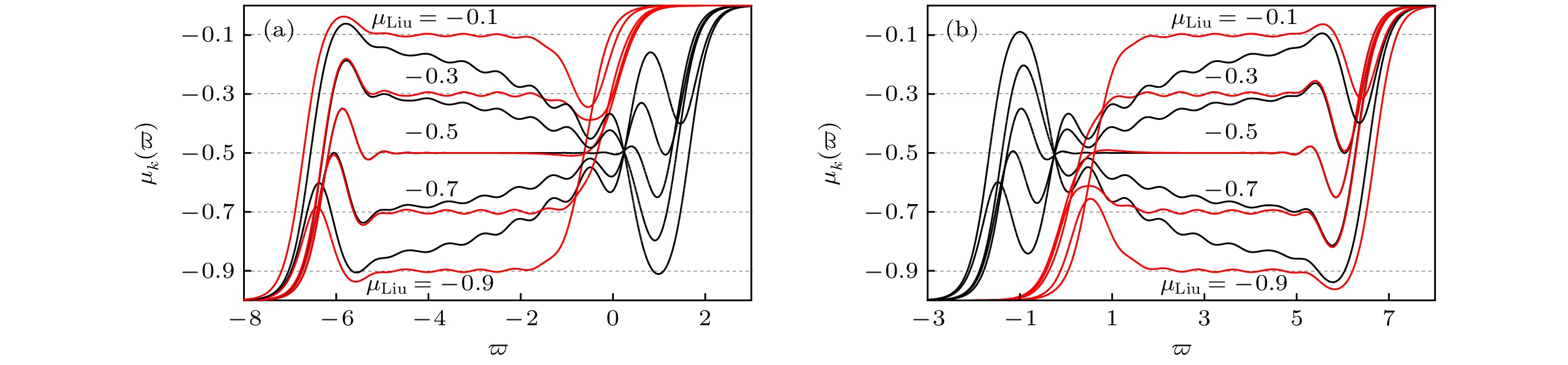
图 4 正比拓展时左侧端口分抗与右侧端口分抗的运算特征曲线(
$ k=12, \sigma =5 $ ) (a) 阶频特征曲线; (b) 相频特征曲线Fig. 4. Operational characteristic curves of left-side port fractance and right-side port fractance in direct proportion extension (k = 12, σ = 5): (a) Order-frequency characteristic curves; (b) phase-frequency characteristic curves.
图 6 标度分形格分抗与新网络N的运算特征曲线(
$ k\to {\infty }, \sigma =5 $ ) (a) 阶频特征曲线; (b) 相频特征曲线Fig. 6. Operational characteristic curves of scaling fractal-lattice fractance and new network N (
$ k\to {\infty }, \sigma =5 $ ): (a) Order-frequency characteristic curves; (b) phase-frequency characteristic curves.
图 8 新网络N与标度分形格分抗运算特征曲线对比图(
$ k=8, \sigma =5 $ ) (a) 阶频特征曲线; (b) 相频特征曲线Fig. 8. Comparison diagram of operational characteristic curves of new network N and scaling fractal-lattice fractance (k = 8, σ = 5): (a) Order-frequency characteristic curves; (b) phase-frequency characteristic curves.
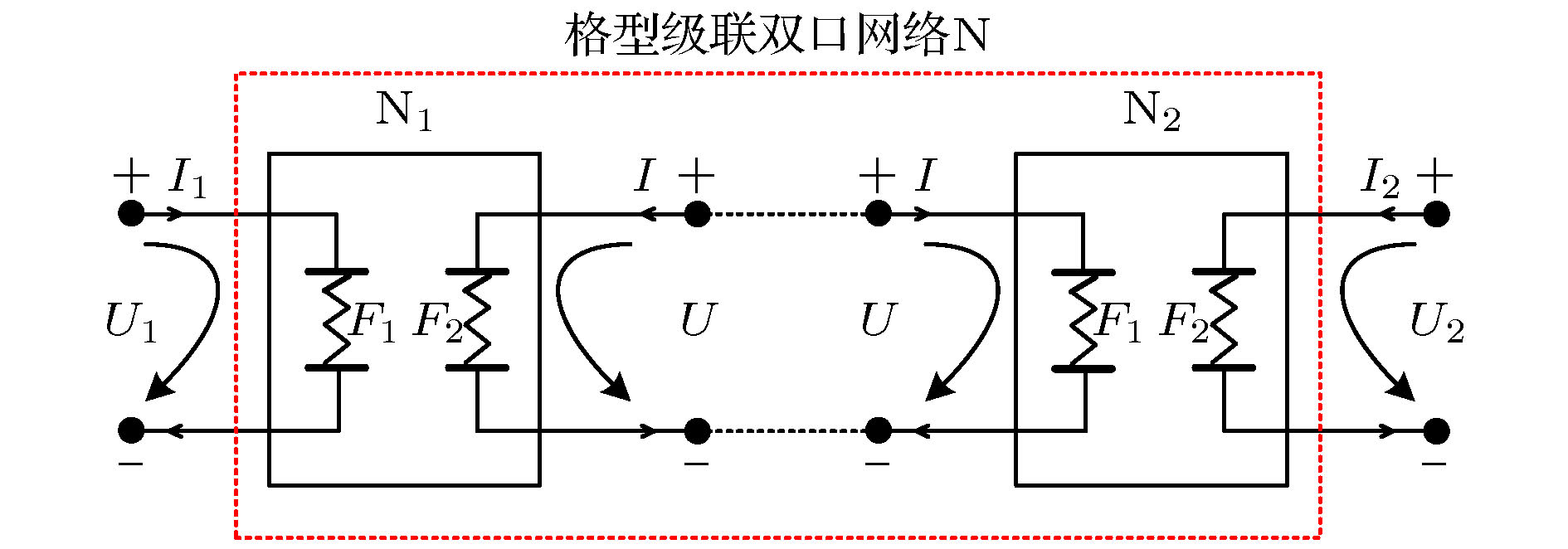
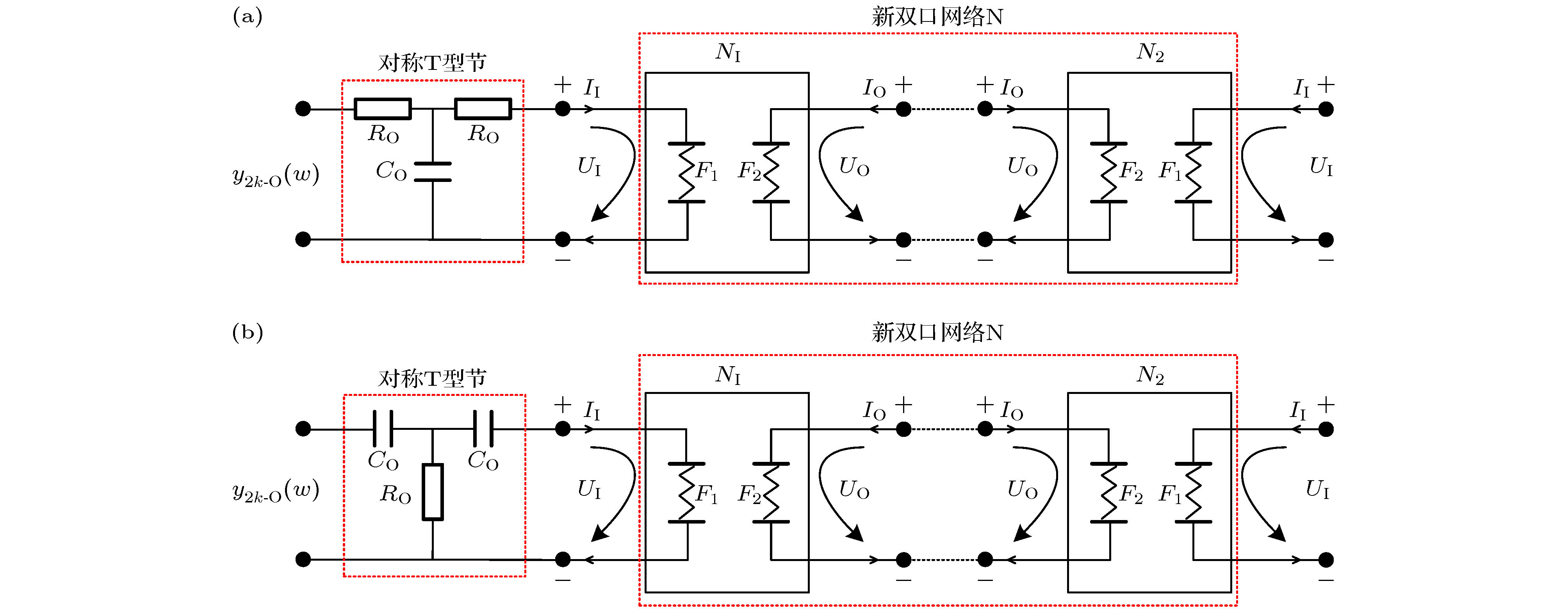
图 10 (a) 正比拓展左侧分抗零极点指数(黑色)与右侧分抗的零极点指数(绿色)分布对比图; (b) 正比拓展左侧分抗零极点指数(黑色)与新网络N的零极点指数(红色)对比图
Fig. 10. (a) The distribution comparison diagram of zero-pole exponents (black) of left-side fractance and zero-pole exponents (green) of right-side fractance in direct proportion extension; (b) the distribution comparison diagram of zero-pole exponents (black) of left-side fractance and zero-pole exponents (red) of new network N.
图 11 新双口网络N的电路优化原理图 (a) 正比拓展优化; (b) 反比拓展优化
Fig. 11. Circuit optimization principle diagram of new two-port network N: (a) Optimization in direct proportion extension; (b) optimization in inverse proportion extension.
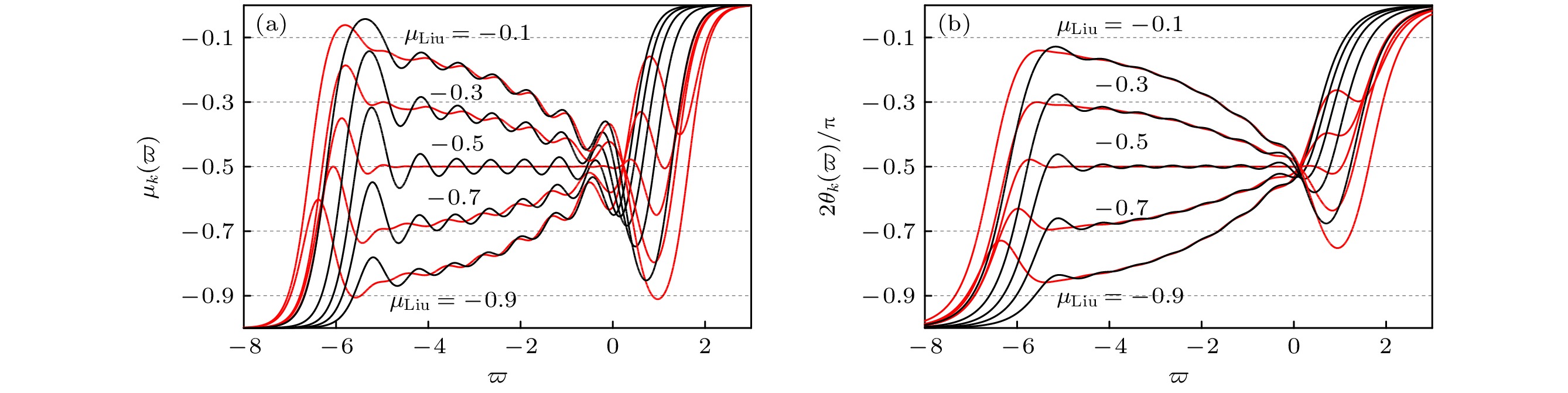
图 12 阶频特征曲线优化对比图 (a) 正比拓展优化 (
$ k=8, \sigma =5 $ ); (b) 反比拓展优化 ($ k=8, \sigma =1/5 $ )Fig. 12. Optimization comparison diagram of order-frequency characteristic curves: (a) Optimization in direct proportion extension (
$ k=8, \sigma =5 $ ); (b) optimization in inverse proportion extension ($ k=8, \sigma =1/5 $ ).
图 13 模拟电路仿真的频域曲线对比图 (a) 幅频特征曲线; (b) 相频特征曲线
Fig. 13. Frequency-domain curves comparison diagram of analog circuits: (a) Amplitude-frequency characteristic curves; (b) phase-frequency characteristic curves.
图 14 半阶微分运算电路原理图
Fig. 14. Schematic diagram of half-order differential operational circuit.
图 15 周期对称方波的半阶微分运算 (a) 理论结果; (b) 模拟电路仿真结果
Fig. 15. The half-order differential operation of a periodic symmetrical square wave: (a) Theoretical result; (b) analog circuit simulation result
-
[1] Karamali G, Dehghan M, Abbaszadeh M 2019 Eng. Comput.-Germany. 35 87
Google Scholar
[2] Oldham K B 1991 J. Appl. Electrochem. 21 1068
Google Scholar
[3] Su Y, Wang Y 2019 J. Funct. Space 2019 1
[4] Hamrouni W, Abdennadher A 2016 Discrete Cont. Dyn-B 21 2509
Google Scholar
[5] Wu G C, Baleanu D, Deng Z G, Zeng S D 2015 Physica A 438 335
Google Scholar
[6] Hamed E M, Said L A, Madian A H, Radwan A G 2020 Circ. Syst. Signal Pr. 39 2
Google Scholar
[7] Ali Yüce, Tan N 2020 J. Eng. 2020 157
Google Scholar
[8] Subhadhra K S, Sharma R K, Gupta S S 2020 Analog Integr. Circuits Signal Process. 103 31
Google Scholar
[9] Hamed E M, Said L A, Madian A H, Radwan A G 2020 Circuits, Systems, and Signal Processing 39 2
[10] Yu B, Pu Y F, He Q Y 2020 J. Circuits Syst. Comput. 29 2050083
Google Scholar
[11] Atan O 2018 Analog Integr. Circuits Signal Process. 96 485
Google Scholar
[12] Mahmoud G M, Abed-Elhameed T M, Ahmed M E 2016 Nonlinear Dyn. 83 1885
Google Scholar
[13] Yang S, Yu J, Hu C, Jiang H 2018 Neural Networks 104 104
Google Scholar
[14] 袁晓 2015 分抗逼近电路之数学原理 (北京: 科学出版社) 第3—15
Yuan X 2015 Mathematical Principles of Fractance Approximation Circuits (Beijing: Science Press) pp3–15 (in Chinese)
[15] Dutta R, Suhash C, Shenoi B A 1966 J. Franklin Inst. 282 318
Google Scholar
[16] Oldham K B 1973 Anal. Chem. 45 39
[17] 袁子, 袁晓 2017 电子学报 45 2511
Google Scholar
Yuan Z, Yuan X 2017 Acta Electron. Sin. 45 2511
Google Scholar
[18] Hill R M, Dissado L A, Nigmatullin R R 1991 J. Phys. Condens. Matter 3 9773
Google Scholar
[19] Liu S H 1985 Phys. Rev. Lett. 55 529
Google Scholar
[20] He Q Y, Pu Y F, Yu B, Yuan X 2019 Circuits Syst. Signal Process. 38 4933
Google Scholar
[21] 何秋燕, 袁晓 2016 65 160202
Google Scholar
He Q Y, Yuan X 2016 Acta Phys. Sin. 65 160202
Google Scholar
[22] He Q Y, Yu B, Yuan X 2017 Chin. Phys. B 26 040202
Google Scholar
[23] He Q Y, Pu Y F, Yu B 2020 Acta Autom. Sin. 7 1425
Google Scholar
[24] 袁晓, 冯国英 2015 中国电子学会电路与系统分会第二十六届学术年会论文集 中国长沙, 2015年10月23日−26日 第295页
Yuan X, Feng G Y 2015 Proceedings of the 26 th Academic Annual Conference of Circuits and Systems Branch, Chinese Institute of Electronics Chang Sha, China, October 23−26, 2015 p295
[25] 余波, 何秋燕, 袁晓 2018 67 070202
Google Scholar
Yu B, He Q Y, Yuan X 2018 Acta Phys. Sin. 67 070202
Google Scholar
[26] 余波, 何秋燕, 袁晓, 杨丽贤 2018 四川大学学报(自然科学版) 55 301
Google Scholar
Yu B, He Q Y, Yuan X, Yang L X 2018 J. Sichuan Univ.(Nat. Sci. Ed.) 55 301
Google Scholar
[27] Herzel F, Osmany S A, Scheytt J C 2010 IEEE Trans. Circuits Syst. Regul. Rap. 57 1914
Google Scholar
下载:
计量
- 文章访问数: 3958
- PDF下载量: 37
- 被引次数: 0
