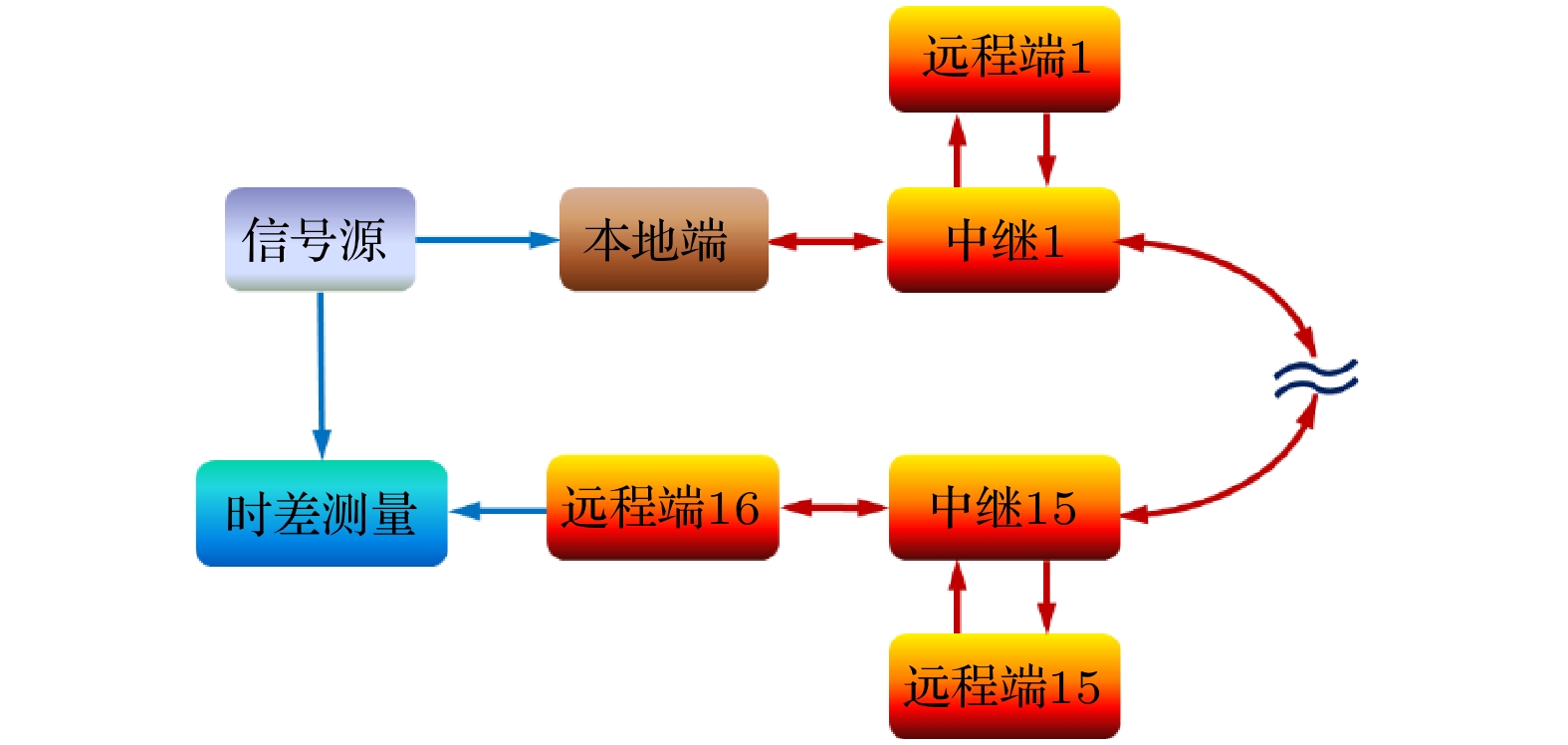
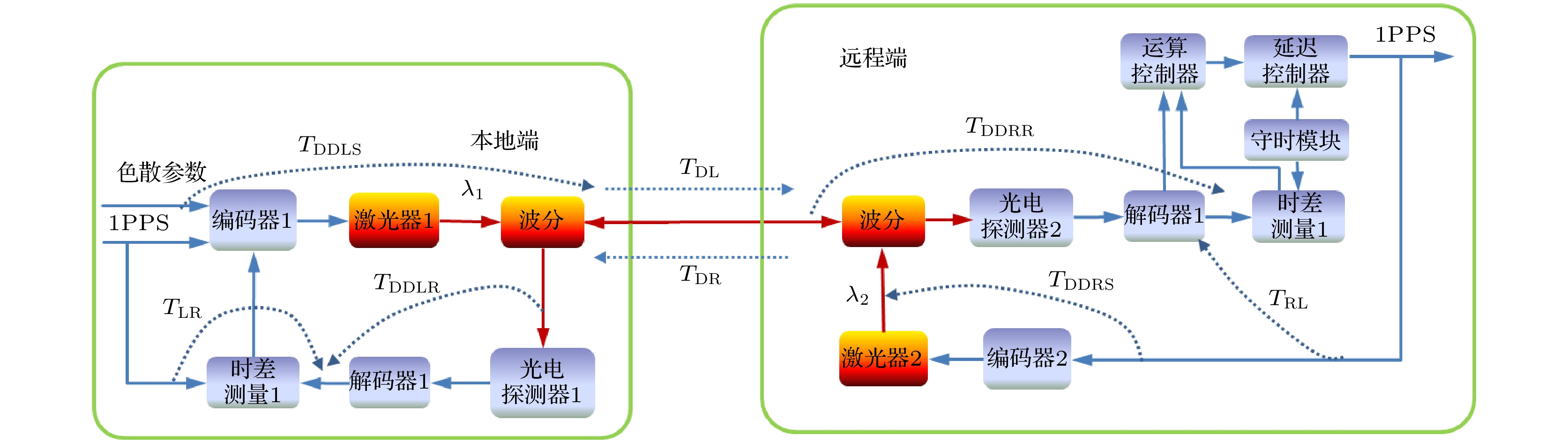
-
在长距离高精度光纤时间同步系统中, 为了减少后向反射光与光纤色散对传输精度的影响, 本文在双波长光纤时间同步传输方法之上, 提出了一种具有色散误差修正功能的双波长光纤时间同步传输方法. 以自行研制的工程样机在长度约为800 km的实验室光纤链路上和1085 km的实地光纤链路上进行了实验测试, 也是国内首次实现千公里级实地光纤时间同步传输. 在实验室光纤链路上, 测得传输链路色散补偿后的色散时延误差为10 ps, 时间同步标准差为5.7 ps, 稳定度为1.12 ps@105 s, 不确定度为18.4 ps. 在实地光纤链路上, 测得传输链路色散补偿后的色散时延误差为60 ps, 时间同步标准差为18 ps, 稳定度为5.4 ps@4 × 104 s, 不确定度为63.5 ps.To reduce the influence of fiber dispersion on accuracy of fiber-based time synchronization, a method of dispersion-error corrected dual-wavelength time synchronization is proposed in this paper. Specificlly, the method is to measure the dispersion coefficient of the fiber link, and then input it to each remote terminal, the time delay error caused by the fiber dispersion is eliminated through the delay phase controller. With the self-developed engineering prototypes, the experimental verifications are subsequently made both in laboratory and real field. Before the test, 16 devices of time synchronization are connected in series for calibration. The time synchronization system is able to keep delay difference within ± 15 ps after being calibrated. In the laboratory, the experimental setup is built by cascading 16 rolls of 50km-long fiber coils, and the total length of the fiber link is 800 km. The experimental results show that the dispersion coefficient of 800 km fiber link is 13.36 ps/(km·nm), and the delay error caused by dispersion is maintained within 10 ps after correction. The stability of the time transfer is 5.7 ps in standard deviation and the time deviation is 1.12 ps at an averaging time of 100000 s. In the real field test, a 1085-km-long field fiber link is utilized, along which 16 self-developed time-frequency transceiversare set at the cascaded fiber-optic stations. After being corrected with a dispersion coefficient of 16.67 ps/(km·nm) for 1085 km urban fiber link, the time transfer is demonstrated to have a dispersion-caused delay error of 60 ps. The experimental results show that the time standard deviation is 18 ps and the time transfer instability is 9.2 ps at an averaging time of 1 s and 5.4 ps at an averaging time of 40000 s. Finally, the time uncertainty of 800-km-long laboratory optical fiber link and 1085-km-long urban optical fiber link are evaluated, and the time uncertainty is 18.4 ps and 63.5 ps, respectively. This work paves the way for constructing the time synchronization fiber network in China. To further reduce the delay error caused by dispersion in a long-distance time transfer link, the more accurate thermal control of the lasers should be adopted to reduce the shifts of forward and backward wavelengths.
-
Keywords:
- fiber link /
- time synchronization /
- synchronization network
[1] He W, Lian B, Yang Q 2013 Proceedings of 2013 IEEE International Conference of IEEE Region 10 Xi’an, China, October 23−25, 2013 p1
[2] Lau K Y, Lutes G F, Tjoelker R L 2014 J. Lightwave Technol. 20 3440
[3] Krehlik P, Buczek L, Kołodziej J, Lipinski M, Sliwczynski L, Nawrocki J, Nogas P, Marecki A, Pazderski E, Ablewski P, Bober M, Ciuryło R, Cygan A, Lisak D, Maslowski P, Morzynski P, Zawada P M, Campbell R M, Pieczerak J, Binczewski A, Turza K 2017 Astron. Astrophy. 60 3
[4] Parthey C G, Matveev A, Alnis J, Bernhardt B, Beyer A, Holzwarth R, Maistrou A, Pohl R, Predehl K, Udem T, Wilken T, Kolachevsky N, Abgrall M, Rovera D, Salomon C, Laurent P, Hansch T W 2011 Phys. Rev. Lett. 107 203001
Google Scholar
[5] Rosenband T, Hume D B, Schmidt P O, Chou C W, Brusch A, Lorini L, Oskay W H, Drullinger R E, Fortier T M, Stalnaker J E, Diddams S A, Swann W C, Newbury N R, Itano W M, Wineland D J, Bergquist J C 2008 Science 319 1808
Google Scholar
[6] Shelkovnikov A, Butcher R J, Chardonnet C, Amy-Klein A 2008 Phys. Rev. Lett. 100 150801
Google Scholar
[7] Lewandowski W, Thomas C 1991 Proc. IEEE 79 991
Google Scholar
[8] Lewandowski W, Azoubib J, Klepczynski W J 1999 Proc. IEEE 87 163
Google Scholar
[9] Jiang Z 2009 Proceedings of 2009 Frequency Control Symposium & the 22nd European Frequency and Time forum Besancon, France, April 20−24, 2009 p1194
[10] Chu F D, Tseng W H, Hsu W C, Ting P Y 2014 Proceedings of IEEE International Frequency Control Symposium Taipei, China, May 19−22, 2014 p11
[11] Kong Y, Yang X H, Qin W J, Cao F, Li Z G, Sun B Q, Chang H 2014 Proceedings of IEEE International Frequency Control Symposium Taipei, China, May 19−22, 2014 p1
[12] Guagn W, Dong S, Wu W, Zhang J, Yuan H, Zhang S 2018 Metrologia 55 175
Google Scholar
[13] Heavner T P, Donley E A, Levi F, Costanzo G, Parker T E, Shirley J H, Ashby N, Barlow S, Jefferts S R 2014 Metrologia 51 174
Google Scholar
[14] Campbell S L, Hutson R B, Marti G E, Goban A, Oppong N D, McNally R L, Sonderhouse L, Robinson J M, Zhang W, Bloom B J, Ye J 2017 Science 358 90
Google Scholar
[15] Ebenhag S C 2008 Proceedings of the 22nd European Frequency and Time Forum Toulouse, France, April 22–25, 2008 p23
[16] Piester D, Fujieda M, Rost M, Bauch A 2009 41st Annual Precise Time and Time Interval (PTTI) Systems and Applications Meeting Santa Ana Pueblo, America, November 16−19, 2009 p16
[17] Smotalacha V, Kuna A, Mache W 2010 Proceedings of the 42nd Annual Precise Time and Time Interval Meeting Reston, America, November 16−19, 2010 p427
[18] Schnatz H 2012 Conference on Precision Electromagnetic Measurement Washington DC, America, July 1−6, 2012 p185
[19] Akiyama T, Matsuzawa H, Haraguchi E, Ando T, Hirano Y 2012 Microwave Symposium Digest. IEEE/MTT-S International Montreal, Canada, June 17–22, 2012, p1
[20] Smotlacha V, Kuna A, Mache W 2010 EFTF-2010 24th European Frequency and Time Forum Noordwijk, Netherlands, April 13–16, 2010 p1
[21] Dierikx E F, Wallin A E, Fordell T, Myyry J, Koponen P, Merimaa M, Pinkert T, Koelemeij J C, Peek H Z, Smets R 2016 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 63 945
Google Scholar
[22] Turza K, Krehlik P, Siwczynski L 2019 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 4 797
[23] Cheng H, Wu G L, Zuo F, Hu L, Chen J 2019 Opt. Lett. 21 5206
[24] 李得龙, 程清明, 张宝富, 卢麟, 雷平纪, 李晓亚 2014 激光与光电子进展 51 010602
Li D L, Cheng Q M, Zhang B F, Lu L, Lei P J, Li X Y 2014 Laser and Photo-electronic Progress 51 010602
[25] 吴龟灵, 陈建平 2016 科技导报 34 99
Google Scholar
Wu G L, Chen J P 2016 Science and Technology Herald 34 99
Google Scholar
[26] Gao C, Wang B, Zhu X, ChenW L, Bai Y, Miao J, Zhu X, Li T C, Wang L J 2012 Opt. Lett. 37 4690
Google Scholar
[27] Chen W, Liu Q, Cheng N, Xu D, Yang F, Gui Y Z, Cai H W 2015 IEEE Photonics J. 7 7901609
[28] 刘杰, 高静, 许冠军, 焦东东, 闫露露, 董瑞芳, 刘涛, 张首刚 2015 64 120602
Google Scholar
Liu J, Gao J, Xu G J, Jiao D D, Yan L L, Dong R F, Jiang H F, Liu T, Zhang S G 2015 Acta Phys. Sin. 64 120602
Google Scholar
[29] Deng X, Jiao D D, Liu J, Zang Q, Zhang X, Wang D, Gao J, Dong R F, Liu T, Zhang S G 2015 Chin Phys. B 24 054205
Google Scholar
[30] Yuan Y B, Wang B, Gao C, Wang L J 2017 Chin. Phys. B 26 040601
Google Scholar
[31] 陈法喜, 赵侃, 周旭, 刘涛, 张首刚 2017 20 200701
Google Scholar
Chen F X, Zhao K, Zhou X, Liu T, Zhang S G 2017 Acta Phys. Sin. 20 200701
Google Scholar
[32] Wang J, Yue C, Xi Y, Sun Y, Cheng N, Yang F, Jiang M, Sun J, Gui Y, Cai H 2020 Opt. Lett. 1 208
-
图 1 双波长光纤时间同步原理图(λ1, λ2, 激光波长)
Fig. 1. Schematic diagram of dual wavelength time transfer. (
$ {\lambda }_{1} $ ,$ {\lambda }_{2} $ , Laser wavelength).
图 2 双波长光纤时间同步装置图(OEO: 光-电-光信号净化处理模块; λ1, λ2: 激光波长; PLL: 锁相环)
Fig. 2. Device diagram of dual wavelength time transfer. (OEO: Optical-electric-optical signal purification and processing module; λ1, λ2: Laser wavelength; PLL: Phase locked loop).
图 4 实验室光纤链路的时间同步测量结果 (a)光纤链路的时差测量结果(蓝色曲线: 系统噪底. 黑色曲线: 800 km实验室光纤链路); (b)光纤链路的时间同步稳定度测量结果(蓝色曲线: 系统噪底; 红色曲线: 800 km实验室光纤链路)
Fig. 4. Time synchronization measurement results of the laboratory fiber link: (a) The measured time interval variation results of the laboratory fiber link (bule line: noise floor of the system; black line: 800 km fiber link in laboratory): (b) the measured time deviation results of the laboratory fiber link (bule line: noise floor of the system; black line: 800 km fiber link in laboratory).
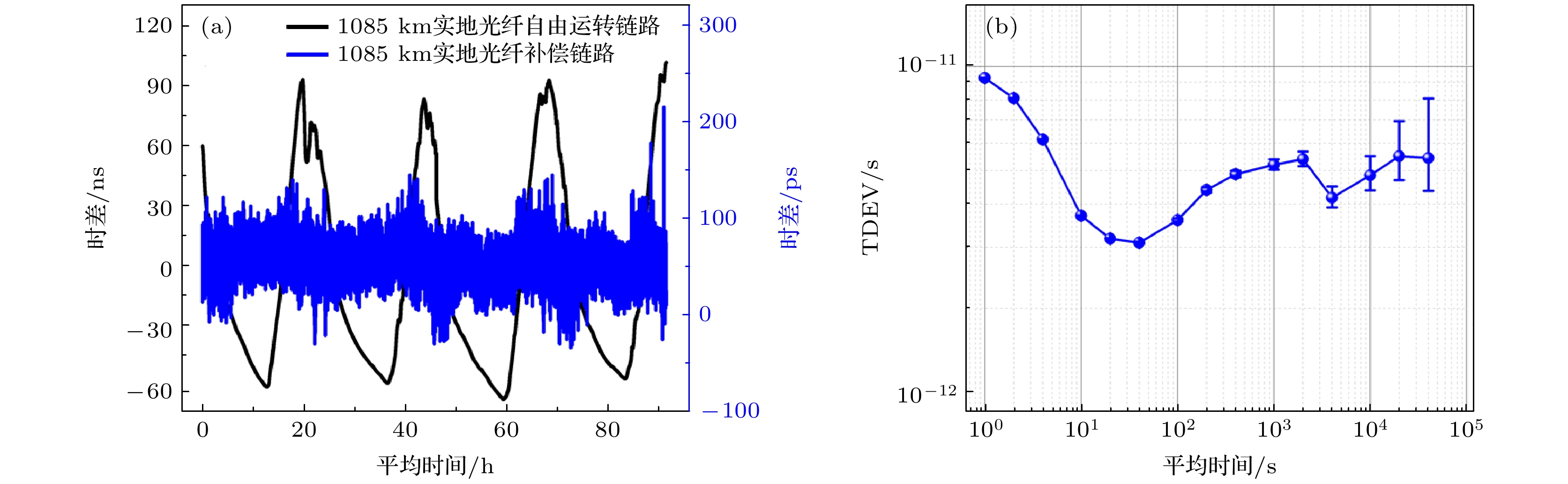
图 6 1085 km实地光纤链路的时间同步测量结果 (a)光纤链路的时差测量结果(黑色曲线: 自由运转链路, 蓝色曲线: 补偿后的链路); (b)补偿后链路的时间同步稳定度测量结果
Fig. 6. Time synchronization measurement results of 1085 km field fiber link: (a) The measured time interval variation results of the laboratory fiber link (black line: free running fiber link; blue line: compensated fiber link); (b) the measured time deviation results of the field fiber link after compensated.
表 1 各个站点设备时延误差测量结果
Table 1. Measurement results of equipment delay error in each station.
编号 校准前/ps 校准后/ps 编号 校准前/ps 校准后/ps 1 2453 12 9 18354 7 2 4669 –5 10 20323 13 3 6056 10 11 22340 –11 4 8375 8 12 24098 6 5 9950 –10 13 25637 5 6 12144 9 14 28031 –8 7 13993 –6 15 29992 –12 8 16058 11 16 31862 8 
下载: 导出CSV
表 2 800 km实验室光纤链路的详细参数
Table 2. Detailed parameters of 800 km fiber link in the laboratory.
距离/km 偏差/ps 色散系数/(ps·km–1·ns–1) 校准后/ps 距离/km 偏差/ps 色散系数/(ps·km–1·ns–1) 校准后/ps 50 267 13.45 19 450 2428 13.59 16 100 530 13.35 –5 500 2683 13.52 –19 150 799 13.41 –10 550 2946 13.49 –9 200 1070 13.47 15 600 3206 13.46 17 250 1341 13.53 –12 650 3466 13.43 18 300 1613 13.54 –14 700 3715 13.37 13 350 1891 13.61 –17 750 3996 13.42 16 400 2171 13.67 11 800 4243 13.36 10
下载: 导出CSV
表 3 1085 km实地光纤链路各个站点的详细参数
Table 3. Detailed parameters of the individual sites in the 1085 km field fiber link.
编号 站点 距离/km 衰减/dB 1 临潼 0 0 2 二长 41.69 12 3 捞浴 72.75 21 4 筒车湾 81.90 21 5 洋县 76.50 19 6 汉中 60.48 16 7 勉县 60.55 16 8 宁强 73.20 19 9 勉县 73.20 19 10 宁强 74.32 19 11 勉县 74.32 19 12 汉中 60.55 16 13 洋县 60.48 16 14 筒车湾 76.50 19 15 捞浴 81.90 21 16 一长 72.75 21 17 临潼 41.69 12 总计 1085 287.5
下载: 导出CSV
表 4 光纤时间传递不确定度分析
Table 4. The uncertainty analysis of the fiber synchronized timing signal.
误差源 误差估计值/ps 800 km
实验室光纤1085 km
实地光纤本地端和远程端设
备时延温漂/$ {u}_{\mathrm{D}\mathrm{T}} $6.0 12.0 时差测量的误差/$ {u}_{\mathrm{T}\mathrm{I}\mathrm{M}} $ 10.0 10.0 激光器波长误差/$ {u}_{∆\lambda } $ 8.0 13.6 光纤色散系数测量
误差/${ {u}_{D} }_{{\rm{err}}}$11.5 56.8 光纤色散系数温度
漂移/$ {u}_{\Delta D} $2.9 19.5 总不确定度 18.4 63.5
下载: 导出CSV
-
[1] He W, Lian B, Yang Q 2013 Proceedings of 2013 IEEE International Conference of IEEE Region 10 Xi’an, China, October 23−25, 2013 p1
[2] Lau K Y, Lutes G F, Tjoelker R L 2014 J. Lightwave Technol. 20 3440
[3] Krehlik P, Buczek L, Kołodziej J, Lipinski M, Sliwczynski L, Nawrocki J, Nogas P, Marecki A, Pazderski E, Ablewski P, Bober M, Ciuryło R, Cygan A, Lisak D, Maslowski P, Morzynski P, Zawada P M, Campbell R M, Pieczerak J, Binczewski A, Turza K 2017 Astron. Astrophy. 60 3
[4] Parthey C G, Matveev A, Alnis J, Bernhardt B, Beyer A, Holzwarth R, Maistrou A, Pohl R, Predehl K, Udem T, Wilken T, Kolachevsky N, Abgrall M, Rovera D, Salomon C, Laurent P, Hansch T W 2011 Phys. Rev. Lett. 107 203001
Google Scholar
[5] Rosenband T, Hume D B, Schmidt P O, Chou C W, Brusch A, Lorini L, Oskay W H, Drullinger R E, Fortier T M, Stalnaker J E, Diddams S A, Swann W C, Newbury N R, Itano W M, Wineland D J, Bergquist J C 2008 Science 319 1808
Google Scholar
[6] Shelkovnikov A, Butcher R J, Chardonnet C, Amy-Klein A 2008 Phys. Rev. Lett. 100 150801
Google Scholar
[7] Lewandowski W, Thomas C 1991 Proc. IEEE 79 991
Google Scholar
[8] Lewandowski W, Azoubib J, Klepczynski W J 1999 Proc. IEEE 87 163
Google Scholar
[9] Jiang Z 2009 Proceedings of 2009 Frequency Control Symposium & the 22nd European Frequency and Time forum Besancon, France, April 20−24, 2009 p1194
[10] Chu F D, Tseng W H, Hsu W C, Ting P Y 2014 Proceedings of IEEE International Frequency Control Symposium Taipei, China, May 19−22, 2014 p11
[11] Kong Y, Yang X H, Qin W J, Cao F, Li Z G, Sun B Q, Chang H 2014 Proceedings of IEEE International Frequency Control Symposium Taipei, China, May 19−22, 2014 p1
[12] Guagn W, Dong S, Wu W, Zhang J, Yuan H, Zhang S 2018 Metrologia 55 175
Google Scholar
[13] Heavner T P, Donley E A, Levi F, Costanzo G, Parker T E, Shirley J H, Ashby N, Barlow S, Jefferts S R 2014 Metrologia 51 174
Google Scholar
[14] Campbell S L, Hutson R B, Marti G E, Goban A, Oppong N D, McNally R L, Sonderhouse L, Robinson J M, Zhang W, Bloom B J, Ye J 2017 Science 358 90
Google Scholar
[15] Ebenhag S C 2008 Proceedings of the 22nd European Frequency and Time Forum Toulouse, France, April 22–25, 2008 p23
[16] Piester D, Fujieda M, Rost M, Bauch A 2009 41st Annual Precise Time and Time Interval (PTTI) Systems and Applications Meeting Santa Ana Pueblo, America, November 16−19, 2009 p16
[17] Smotalacha V, Kuna A, Mache W 2010 Proceedings of the 42nd Annual Precise Time and Time Interval Meeting Reston, America, November 16−19, 2010 p427
[18] Schnatz H 2012 Conference on Precision Electromagnetic Measurement Washington DC, America, July 1−6, 2012 p185
[19] Akiyama T, Matsuzawa H, Haraguchi E, Ando T, Hirano Y 2012 Microwave Symposium Digest. IEEE/MTT-S International Montreal, Canada, June 17–22, 2012, p1
[20] Smotlacha V, Kuna A, Mache W 2010 EFTF-2010 24th European Frequency and Time Forum Noordwijk, Netherlands, April 13–16, 2010 p1
[21] Dierikx E F, Wallin A E, Fordell T, Myyry J, Koponen P, Merimaa M, Pinkert T, Koelemeij J C, Peek H Z, Smets R 2016 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 63 945
Google Scholar
[22] Turza K, Krehlik P, Siwczynski L 2019 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 4 797
[23] Cheng H, Wu G L, Zuo F, Hu L, Chen J 2019 Opt. Lett. 21 5206
[24] 李得龙, 程清明, 张宝富, 卢麟, 雷平纪, 李晓亚 2014 激光与光电子进展 51 010602
Li D L, Cheng Q M, Zhang B F, Lu L, Lei P J, Li X Y 2014 Laser and Photo-electronic Progress 51 010602
[25] 吴龟灵, 陈建平 2016 科技导报 34 99
Google Scholar
Wu G L, Chen J P 2016 Science and Technology Herald 34 99
Google Scholar
[26] Gao C, Wang B, Zhu X, ChenW L, Bai Y, Miao J, Zhu X, Li T C, Wang L J 2012 Opt. Lett. 37 4690
Google Scholar
[27] Chen W, Liu Q, Cheng N, Xu D, Yang F, Gui Y Z, Cai H W 2015 IEEE Photonics J. 7 7901609
[28] 刘杰, 高静, 许冠军, 焦东东, 闫露露, 董瑞芳, 刘涛, 张首刚 2015 64 120602
Google Scholar
Liu J, Gao J, Xu G J, Jiao D D, Yan L L, Dong R F, Jiang H F, Liu T, Zhang S G 2015 Acta Phys. Sin. 64 120602
Google Scholar
[29] Deng X, Jiao D D, Liu J, Zang Q, Zhang X, Wang D, Gao J, Dong R F, Liu T, Zhang S G 2015 Chin Phys. B 24 054205
Google Scholar
[30] Yuan Y B, Wang B, Gao C, Wang L J 2017 Chin. Phys. B 26 040601
Google Scholar
[31] 陈法喜, 赵侃, 周旭, 刘涛, 张首刚 2017 20 200701
Google Scholar
Chen F X, Zhao K, Zhou X, Liu T, Zhang S G 2017 Acta Phys. Sin. 20 200701
Google Scholar
[32] Wang J, Yue C, Xi Y, Sun Y, Cheng N, Yang F, Jiang M, Sun J, Gui Y, Cai H 2020 Opt. Lett. 1 208
下载:
计量
- 文章访问数: 6903
- PDF下载量: 159
- 被引次数: 0
